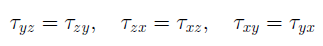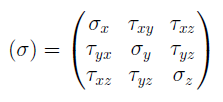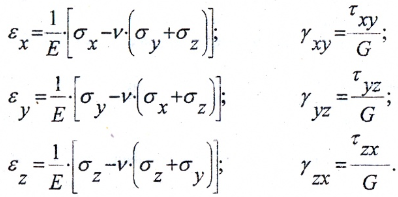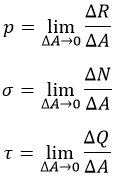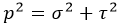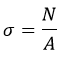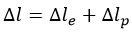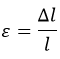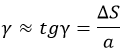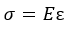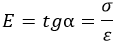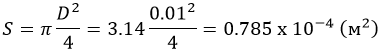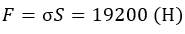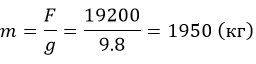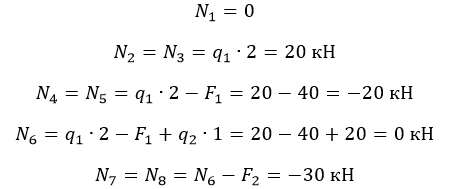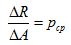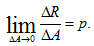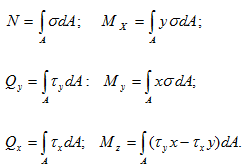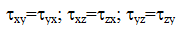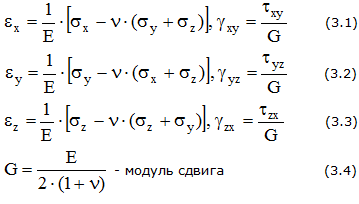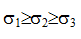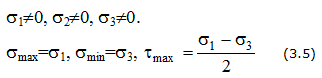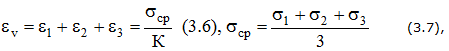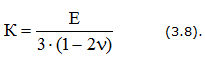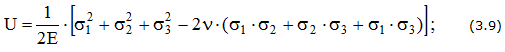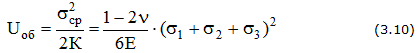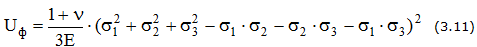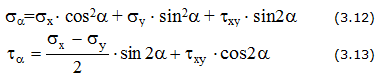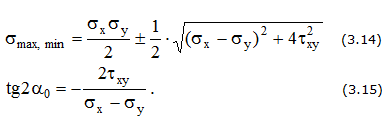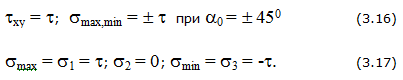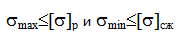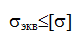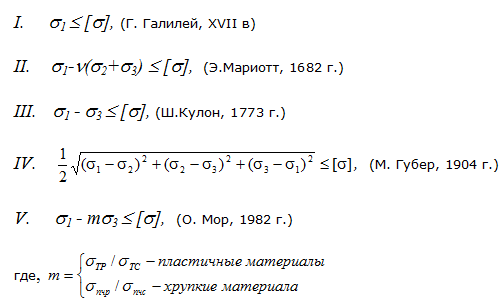что такое главные напряжения сопромат

Тензор напряжений.
Главные площадки и главное напряжение.
Виды напряжённого состояния.

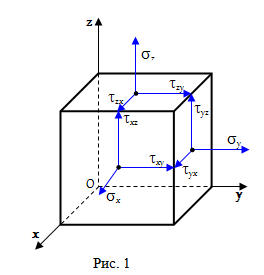
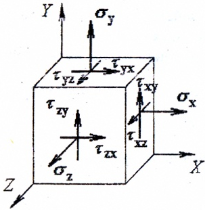
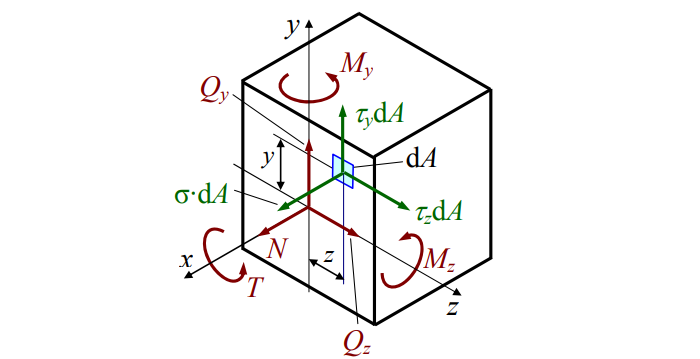
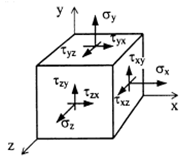
Введем в произвольной точке тела декартову прямоугольную систему координат O_xyz. Рассмотрим в точке O элементарный (бесконечно малый) куб, ребра которого параллельны осям системы координат. Пусть длины ребер куба равны d_a. Нарисуем на гранях куба нормальные <σ_x, σ_y, σ_z> и касательныеxy, t_xz, t_yx, t_yz, t_zx, t_zy> напряжения, параллельные одной из осей координат (рис. 1).

Нормальные напряжения направлены наружу куба и перпендикулярны его граням, а касательные напряжения лежат в плоскостях граней куба. Индекс нормальных напряжений соответствует оси, которой они параллельны. Первая буква двойного индекса касательных напряжений совпадает с индексом нормального напряжения на той же грани. В силу третьего закона Ньютона напряжения на противоположных гранях элементарного куба равны по модулю и противоположны по направлению.

Закон парности касательных напряжений : на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к общему ребру, равны по модулю и направлены обе либо к ребру, либо от ребра:

В курсе «Сопротивление материалов» тензором напряжений называется матрица:

Главные площадки и главные напряжения.

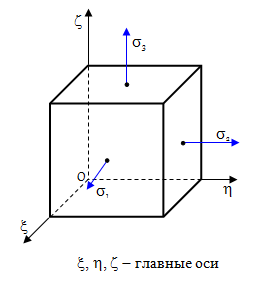
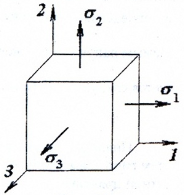
Главными площадками напряжений называются площадки, на которых отсутствуют касательные напряжения.

Виды напряженного состояния.

Виды напряженного состояния: линейное напряженное состояние (два главных напряжения равны нулю), плоское напряженное состояние (одно из главных напряжений равно нулю) и объемное напряженное состояние (все главные напряжения не равны нулю).

Источник

iSopromat.ru

Главными называют нормальные напряжения на площадках рассматриваемого элемента с нулевыми касательными напряжениями.

Для любого случая нагружения бруса всегда можно найти такое положение мысленно выделенного в нем элемента, на гранях которого касательные напряжения будут отсутствовать (т.е. τ=0)

Площадки (грани элемента) на которых касательные напряжения равны нулю называются главными.

Таким образом, главные напряжения – это нормальные напряжения на главных площадках.

Обозначение главных напряжений

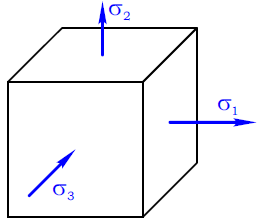
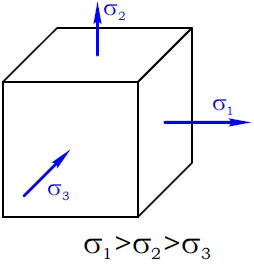
Главные напряжения принято обозначать буквой σ с индексом 1, 2 и 3.

При этом наибольшее, с учетом знака, напряжение обозначается как σ₁ а наименьшее соответственно σ₃.

Другими словами, главное напряжение, расположенное на числовой оси правее других – σ₁, а то, которое левее всех σ₃.

Например, для случая объемного напряженного состояния:

При плоском напряженном состоянии:

При линейном напряженном состоянии единственное напряжение всегда обозначается как σ₁ или просто σ.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

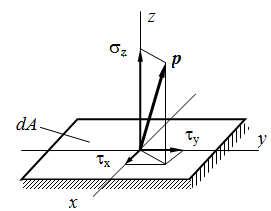
Теория напряженного состояния в окрестности точки деформируемого тела рассматривает совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку.

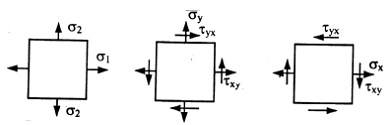
На площадках общего положения действуют нормальные и касательные напряжения (рис. 1).

Правило знаков для этих напряжений в сопротивлении материалов принимается следующим: положительные нормальные напряжения направлены от сечения, а положительные касательные напряжения стремятся повернуть элемент по направлению хода часовой стрелки.

Площадки, на которых отсутствуют касательные напряжения, называются главными площадками, а нормальные напряжения, действующие по этим площадкам, — главными напряжениями.

В любой точке деформируемого тела можно выделить три взаимно перпендикулярные главные площадки, по которым действуют главные напряжения σ₁, σ₂ и σ₃, причем σ₁ ≥ σ₂ ≥ σ₃.

Если два главных напряжения из трех равны нулю, то такое напряженное состояние называется линейным или одноосным. Оно соответствует центральному (осевому) растяжению или сжатию и рассмотрено в предыдущем разделе.

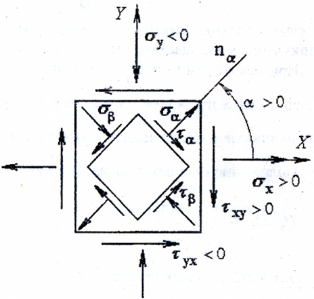
Если одно из трех главных напряжений равно нулю, то такое напряженное состояние называется плоским или двуосным. Пример плоского напряженного состояния показан на рис. 2.

Одноименные напряжения на параллельных гранях бесконечно малого элемента численно равны друг другу. При плоском напряженном состоянии две противоположные грани всегда свободны от напряжений (на рис. 2 это фасадная и тыльная грани).

По закону парности касательных напряжений касательные напряжения на взаимно перпендикулярных площадках равны по величине и противоположны по знаку, т.е. τ_xy=-τ_yx.

Величины σ связаны законом суммы нормальных напряжений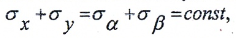

т.е. сумма величин нормальных напряжений, действующих по взаимно перпендикулярным площадкам, есть величина постоянная.

При некотором угле α₀ касательные напряжения равны нулю, нормальные напряжения по данной площадке в данной точке максимальны ( σ_max), а на перпендикулярной площадке – минимальны ( σ_min).

Положение главных площадок определяется по формуле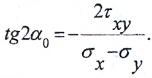

Значения главных напряжений вычисляются по выражению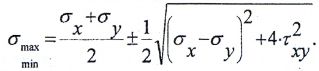

Наибольшие касательные напряжения действуют на площадках, наклонных к главным под углом 45 0 и рассчитываются по формулам: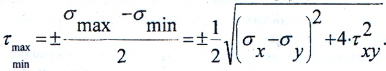

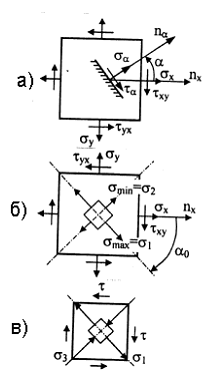
Нормальные напряжения на этих площадках можно найти по формуле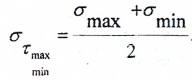

Относительные линейные и угловые деформации ребер элемента можно вычислить на основании обобщенного закона Гука. Для плоского напряженного состояния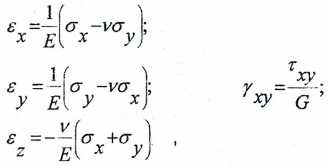

где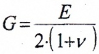

— модуль сдвига материала. Для стали G=80ГПа.

Относительное изменение объема материала в окрестностях исследуемой точки определяется по формуле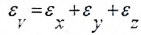

Удельная потенциальная энергия для плоского напряженного состояния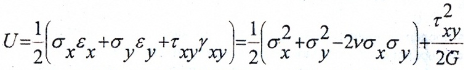

Напряженное состояние называется объемным или трехосным (рис. 3), если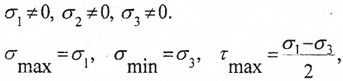

Относительное изменение объема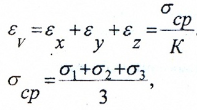

где K – модуль объемной деформации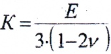

Удельная потенциальная энергия упругой деформации:
— полная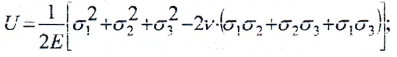

— изменения объема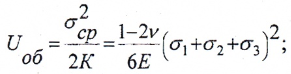

— изменения формы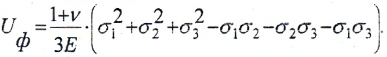

Относительные деформации и напряжения связаны обобщенным законом Гука:

Теории прочности

Для проверки прочности материала при плоском и объемном напряженном состояниях используются гипотезы (теории) прочности.

Каждая гипотеза прочности высказывает свое предположение о том, какой фактор вызывает появление опасного (предельного) состояния.

В зависимости от принятой гипотезы определяют эквивалентное напряжение σ_экв и сравнивают его с допустимым напряжением на растяжение [ σ], то есть условие прочности записывается следующим образом: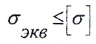

Приведем зависимости для вычисления эквивалентных напряжений по трем гипотезам прочности, наиболее широко применяемым в современной расчетной практике.

Гипотеза наибольших касательных напряжений (III теория прочности)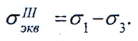

Четвертая (энергетическая) гипотеза прочности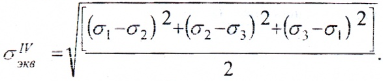

Гипотеза прочности Мора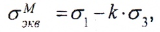

где коэффициент k представляет собой отношение предельных напряжений при одноосном растяжении и сжатии. Можно принять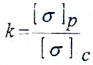

III и IV гипотезы применяют для оценки прочности пластичных материалов, а гипотезу Мора – как для пластичных, так и для хрупких.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Многочисленные учебники «Cопромат для чайников» создают для развенчания мифа о непостижимой сложности дисциплины. Этой наукой пугают на первых курсах вузов. Для начала расшифруем грозный термин «сопротивление материалов».

На деле – проста и решение почти не выходит за рамки школьной задачи о растяжении и сжатии пружины. Другое дело – найти слабое звено конструкции и свести расчет к несложной постановке. Так что не стоит зевать на лекциях по основам механики. При подготовке к урокам можно пользоваться решениями онлайн, но на экзаменах помогут только свои знания.

Что такое сопромат

Это методика расчета деталей, конструкций на способность выдерживать нагрузки в требуемой степени. Или хотя бы для предсказания последствий. Не более, хотя почему-то относят руководство к наукам.

Этой «наукой» прекрасно владели древнегреческие и древнеримские инженеры, сооружавшие сложнейшие механизмы. Понятия не имея о структуре, уравнении состояния вещества и прочих теориях, египтяне строили исполинские плотины и пирамиды.

Основные задачи по сопротивлению материалов

Задача следует напрямую из определения. А вот каковы критерии упомянутого слова «выдерживать»? Неясно, что скрывается под «материалом» и как реальные вещи схематизировать.

Требования

Перечислены далеко не все, но для статики и базовой программы хватит:

Прочность – способность образца воспринимать внешние силы без разрушения. Слегка мнущаяся под весом оборудования подставка никого не интересует. Основную-то функцию она выполняет.

Жесткость – свойство воспринимать нагрузку без существенного нарушения геометрии. Гнущийся под силой резания инструмент даст дополнительную погрешность обработки. К ошибке приведет деформация станины агрегата.

Устойчивость – способность конструкции сохранять стабильность равновесия. Поясним на примере: стержень находится под грузом, будучи прямым – выдерживает, а чуть изогнется – характер напряжения изменится, груз рухнет.

Материал и силы

Как всякая методика, сопромат принимает массу упрощений и прямо неверных допущений:

материал однороден, среда сплошная. Внутренние особенности в расчет не берутся;

свойства не зависят от направления;

образец восстанавливает начальные параметры при снятии нагрузки;

поперечные сечения не меняются при деформации;

в удаленных от места нагрузки местах усилие распределяется равно по сечению;

результат воздействия нагрузок равен сумме последствий от каждой;

деформации не влияют на точки приложения сил;

отсутствуют изначальные внутренние напряжения.

Схемы

Служат для создания возможности расчета реальных конструкций:

тело – объект с практически одинаковыми «длина х ширина х высота»;

брус (балка, стержень, вал) – характеризуется значительной длиной.

На рисунке показаны опоры с воспринимаемыми реакциями (обозначены красным цветом):

Рис. 1. Опоры с воспринимаемыми реакциями:

в) жесткая заделка (защемление).

Силы в сопромате

Приложенные извне, уравновешиваются возникающими изнутри. Напомним, рассматривается статическая ситуация. Материал «сопротивляется».

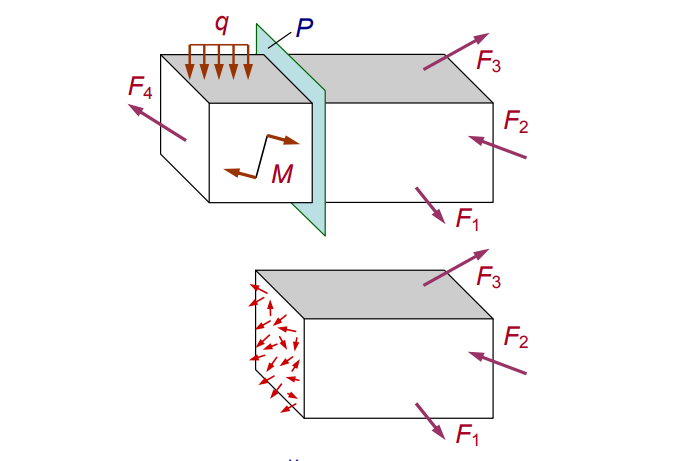
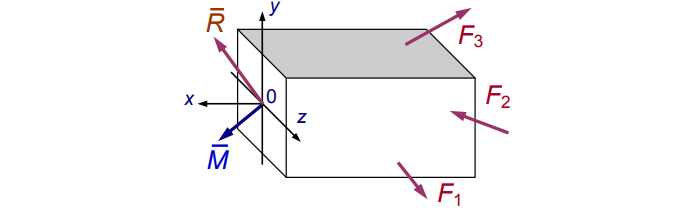
Разделим нагруженное тело виртуальным сечением P (см. рис. 2).

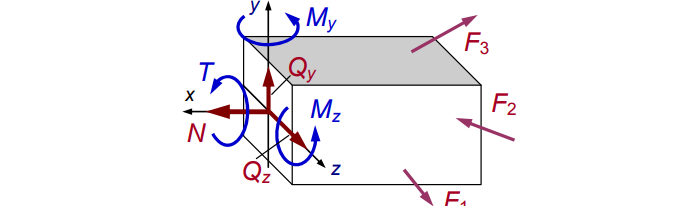
Заменим хаос равнодействующей R и моментом M (см. рис. 3):

Распределив по осям, получим картину нагрузки сечения (см. рис. 4):

Нагрузки и деформации, изучаемые в сопромате

Изучим несколько принятых терминов.

Напряжения

В теле приложенные силы распределяются по сечению. Нагружен каждый элементарный «кусочек». Разложим силы:

Элементарные усилия таковы:

σ – «сигма», нормальное напряжение. Перпендикулярно сечению. Характерно для сжатия / растяжения;

τ – «тау», касательное напряжение. Параллельно сечению. Появляется при кручении;

p – полное напряжение.

Просуммировав элементы, получим:

N – нормальная сила;

A – площадь сечения.

В принятой в России системе СИ сила измеряется в ньютонах (Н). Напряжения – в паскалях (Па). Длины в метрах (м).

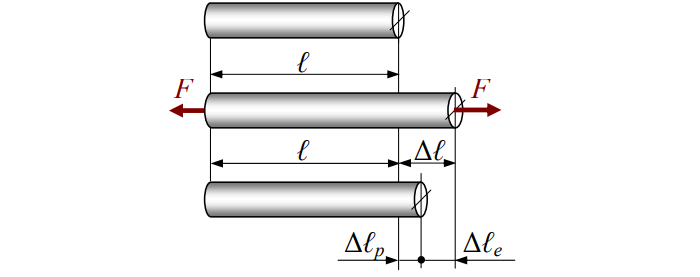
Деформации

Различают деформацию упругую (с индексом «e») и пластическую (с индексом «p»). Первая исчезает по снятии растягивающей / сжимающей силы, вторая – нет.

Полная деформация будет равна:

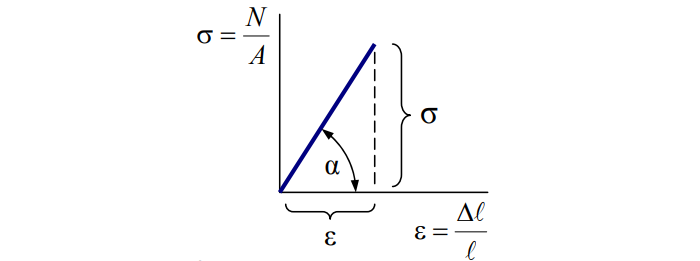
Деформация относительная обозначается «ε» и рассчитывается так:

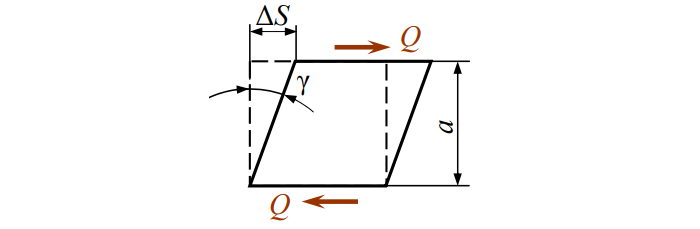
Под «сдвигом» понимается смещение параллельных слоев. Рассмотрим рисунок:

Здесь γ – относительный сдвиг.

Виды нагрузки

Растяжение и сжатие – нагрузка нормальной силой (по оси стержня).

Кручение – действует момент. Обычно рассчитываются передающие усилия валы.

Изгиб – воздействие направлено на искривление.

Основные формулы

Базовый принцип сопромата единственный. В упомянутой задаче о пружине применим закон Гука:

E – модуль упругости (Юнга). Величина зависит от используемого материала. Для стали полагают равным 200 х 10 6 Па.

Сопротивление материала прямо пропорционально деформации:

Закон верен не всегда и не для всех материалов. Как уже упоминалось, принимается как одно из допущений.

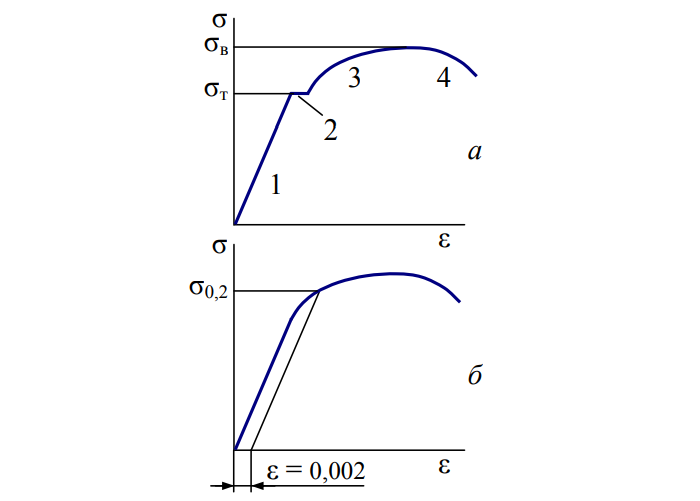
Реальная диаграмма

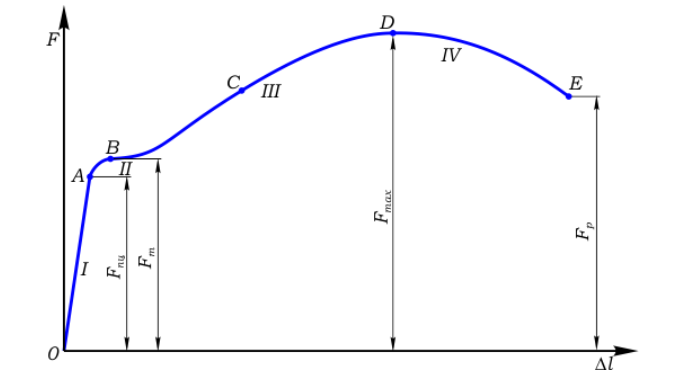
Растяжение стержня из низкоуглеродистой стали выглядит следующим образом:

График (б) относится к большей части конструкционных материалов: подкаленные стали, сплавы цветных металлов, пластики.

Расчеты обычно ведут по σ_т (а) и σ_0.2 (б). С незначительными пластическими деформациями конструкции или без таковых.

Пример решения задачи

Какой груз допустимо подвесить на пруток из стали 45 Ø10 мм?

σ_0,2 для стали 45 равна 245 МПа (из ГОСТ).

Площадь сечения прутка:

Допустимая сила тяжести:

Для получения веса следует разделить на ускорение свободного падения g:

Ответ: необходимо подвесить груз массой 1950 кг.

Как найти опасное сечение

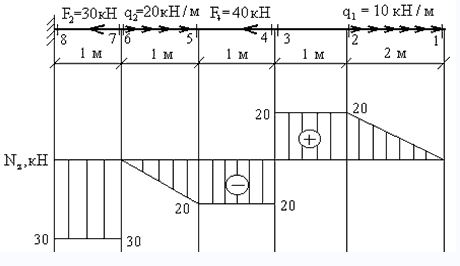
Наиболее простой способ – построение эпюры. На закрепленную балку действуют точечные и распределенные силы. Считаем на характерных участках, начиная с незакрепленного конца.

Усилие положительно, если направлено на растяжение.

На схеме показано, что:

Зачем и кому нужен сопромат

Даже не имеющий отношения к прочностным расчетам инженер-универсал должен иметь понятие о приблизительных (на 10-20%) значениях. Знать конструкционные материалы, представлять свойства. Чувствовать заранее слабые места агрегатов.

Совершенно необходим разработчикам различных конструкций, машиностроительных изделий. Будущим архитекторам в вузах преподается в виде предмета «Строительная механика».

Методика помогает на стадии проектирования обеспечивать необходимый запас прочности изделий. Стойкость к постоянным и динамичным нагрузкам. Это сберегает массу времени и затрат в дальнейших изготовлении, испытании и эксплуатации изделия. Обеспечивает надежность и долговечность.

Источник

iSopromat.ru

Рассмотрим понятие о напряженном состоянии в точке и гипотезы прочности. Связь между напряжениями и внутренними силами. Объемное, плоское и линейное напряженное состояния.

Понятие о напряжениях в точке

На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению.

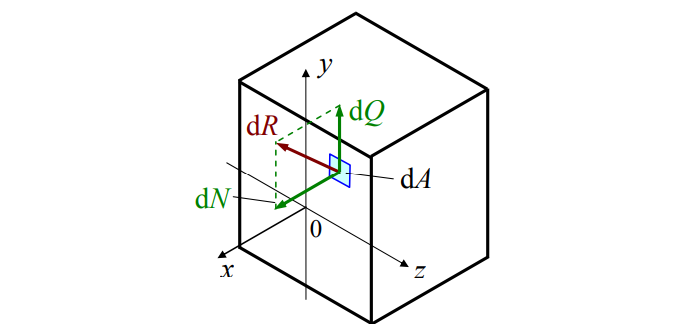
Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение

представляет собой среднее напряжение на данной площадке.

Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке

Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением.

Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов.

Связь между напряжениями и внутренними силами

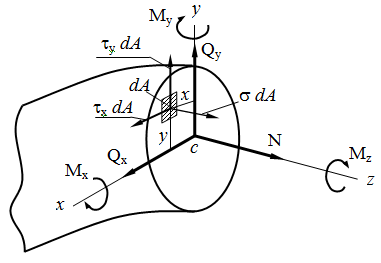
Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τ_x dA, τ_y dA.

Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению.

Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению.

Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.

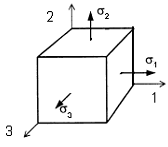
Объемное напряженное состояние

Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1).

Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений:

Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2).

Обозначение главных напряжений:

Напряженное состояние называется объемным или трехосным, если

Относительное изменение объема:

где К – модуль объемной упругости,

Удельная потенциальная энергия упругой деформации:

Плоское напряженное состояние

Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).

Напряжения на наклонной площадке (рис. 3.4,а)

Величина и направление главных напряжений (рис. 3.4,б)

Линейное напряженное состояние

Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю.

Проверка прочности при линейном напряженном состоянии проводится по условию прочности:

В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению:

Величина σ_экв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием.

Гипотезы прочности

Существует 5 гипотез прочности:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник