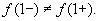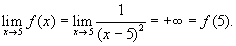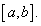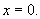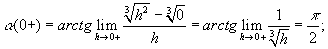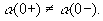что такое гладкая кривая

Кривые и основные понятия

Понятие простой кривой.

Пусть в трехмерном пространстве выбрана прямоугольная система координат \(Oxyz\), и пусть на отрезке \([\alpha,\beta]\) заданы непрерывные функции \(x=x(t),y=y(t),z=z(t)\). Тогда говорят, что задано непрерывное отображение отрезка \([\alpha,\beta]\) в трехмерное пространство.

Рис. 22.1

Числа \(x(t),y(t),z(t)\) можно рассматривать как координаты точки M (рис. 22.1), где \(M=M(t)\), или как координаты вектора \(r(t)\) с началом в точке \(O\) и концом в точке \(M\), то есть
$$
\overrightarrow=r(t)=(x(t),y(t),z(t)).\nonumber
$$
Если считать, что переменное \(t\) есть время, то уравнения
$$
x=x(t),\quad y=y(t),\quad z=z(t),\quad \alpha\leq t\leq\beta,\label
$$
определяют закон движения точки \(M(t)\), а множество точек \(M(t)\), соответствующих всевозможным значениям \(t\) на отрезке \([\alpha,\beta]\), можно рассматривать как след (путь) точки, движущейся по закону \eqref.

В общем случае закон движения может быть очень сложным. Например, существуют такие непрерывные на отрезке \([\alpha,\beta]\) функции \(x(t),y(t),z(t)\), что точка \(M(t)\), движущаяся в соответствии с законом \eqref, пройдет через каждую точку некоторого куба.

Предположим, что любым двум различным значениям \(t_<1>\) и \(t_<2>\) из отрезка \([\alpha,\beta]\) соответствуют различные точки \(M(t_1)\) и \(M(t_2)\) пространства, и обозначим через \(K\) множество всех точек \(M(x,y,z)\) пространства, координаты которых определяются формулами \eqref.

Будем говорить, что точка \(M(t_2)\in K\) следует за точкой \(M(t_<1>)\in K\) или точка \(M(t_1)\) предшествует точке \(M(t_<2>)\), если \(\alpha\leq t_ <1>0\), задается полуокружность радиуса \(R\), лежащая в верхней полуплоскости (\(y\geq 0\)) и «пробегаемая» против часовой стрелки. График функции \(y=f(x)\), непрерывной на отрезке \([\alpha,\beta]\), можно рассматривать как простую плоскую кривую \(\Gamma\), заданную уравнением
$$
\Gamma=.\nonumber
$$

Параметризуемые кривые.

Если существуют два различных значения \(t_1\) и \(t_2\) из отрезка \([\alpha,\beta]\) таких, что \(M(t_<1>)=M(t_<2>)\), то отображение \eqref отрезка в трехмерное пространство не является взаимно однозначным.

Предположим, что отрезок \([\alpha,\beta]\) можно разбить на отрезки \(\delta_=[t_,t_],\ k=\overline<1,n>\), где \(\alpha=t_ <0>Замечание 2.

Одна и та же кривая \(\Gamma\) может быть параметризована различными способами. Мы будем рассматривать только такие параметризации, которые получаются из данной параметризации \eqref путем представления параметра \(t\) в виде непрерывной строго возрастающей функции другого параметра.

Это означает, что если наряду с представлением кривой \(\Gamma\) через параметр \(t\) уравнением \eqref эта кривая представлена через параметр \(s\) уравнением
$$
\Gamma=<\rho=\rho(s),\ \alpha_<1>\leq s\leq\beta_<1>>,\label
$$
то должно выполняться условие: \(s=s(t)\) — непрерывная строго возрастающая функция на отрезке \([\alpha,\beta]\), причем
$$
s(\alpha)=\alpha_<1>,\quad s(\beta)=\beta_1,\quad \rho(s(t))=\textbf(t)\quad для\ всех\ t\in [\alpha,\beta].\label
$$

В этом случае на отрезке \([\alpha_<1>,\beta_<1>]\) определена непрерывная и строго возрастающая функция \(t=t(s)\), обратная к функции \(s=s(t)\), и для всех \(s\in[\alpha_<1>,\beta_<1>]\) выполняется равенство
$$
\rho(s)=\textbf(t(s)).\label
$$

Условимся в дальнейшем, если не оговорено противное, для записи уравнений кривых использовать, только параметризации, указанные в замечании 2, и называть их допустимыми.

Пусть параметризуемая кривая \(\Gamma\) задана уравнением \eqref, и пусть существуют значения \(t_<1>\) и \(t_<2>\) (\(t_<1>\neq t_<2>\)) из отрезка \([\alpha,\beta]\) такие, что \(\textbf(t_1)=\textbf(t_2)\). Тогда говорят, что точка \(M_<1>(x_<1>,y_<1>,z_<1>)\), где \(x_<1>=x(t_1)=x(t_2),\ y_<1>=y(t_<1>)=y(t_2),\ z_1=z(t_1)=z(t_<2>)\), является точкой самопересечения (кратной точкой) кривой \(\Gamma\).

Если равенство \(\textbf(t_1)=\textbf(t_2\)) выполняется при \(t_<1>=\alpha,\ t_<2>=\beta\), то кривую \(\Gamma\) называют замкнутой. Замкнутую кривую, не имеющую точек самопересечения, отличных от точки \(M_<1>(x(\alpha),y(\alpha),z(\alpha))\), будем называть простым контуром.

Например, кривая
$$
\Gamma=\\nonumber
$$
является простым контуром. При изменении \(t\) от 0 до \(2\pi\) точка \(M(\cos t,\sin t)\) «описывает» единичную окружность, двигаясь против часовой стрелки. Точка плоскости \(Oxy\) с координатами \((0,1)\) является одновременно начальной и конечной точкой кривой \(\Gamma\).

Касательная к кривой.

Пусть кривая \(\Gamma\) задана уравнением \eqref, где \(\textbf(t)\) — вектор-функция, дифференцируемая в точке \(t_<0>\in [\alpha,\beta]\), причем \(\textbf‘(t_<0>)\neq 0\). Тогда
$$
\Delta \textbf=\textbf(t_0+\Delta t)-\textbf(t_0)=r'(t_0)\Delta t+\Delta t\alpha(\Delta t),\label
$$
где \(\alpha(\Delta t)\rightarrow 0\) при \(\Delta t\rightarrow 0\). Из условия \(\textbf‘(t0)\neq 0\) и равенства \eqref следует, что при всех достаточно малых \(\Delta t\neq 0\) правая часть \eqref есть ненулевой вектор, и поэтому \(\Delta \textbf \neq 0\), то есть существует число \(\delta > 0\) такое, что если
$$
0 Рис. 22.2

Если \(\textbf‘(t_<0>)\neq 0\), то при всех значениях \(\Delta t\), удовлетворяющих условиям \eqref, ненулевой вектор \(\Delta \textbf=\textbf(t_0+\Delta t)-\textbf(t_0)\) параллелен секущей, и поэтому вектор \(\displaystyle \frac<\Delta r><\Delta t>\) также параллелен секущей. Уравнение секущей имеет вид
$$
r=r(t_0)+\frac<\Delta r><\Delta t>\lambda,\qquad \lambda \in\mathbb.\label
$$

Пусть существует предельное положение секущей, то есть существует \(\displaystyle \lim_<\Delta t\rightarrow 0>\frac<\Delta r><\Delta t>\neq 0\). Тогда прямая, уравнение которой получается из уравнения \eqref заменой отношения \(\displaystyle \frac<\Delta r><\Delta t>\) его пределом, называется касательной к кривой \(\Gamma\) в точке \(M_<0>\).

Если \(r'(t_0)\neq 0\), то существует касательная к кривой \(\Gamma\) в точке \(M_<0>\), и уравнение этой касательной можно записать в виде
$$
\textbf=\textbf(t_<0>)+\textbf‘(t_<0>)\lambda,\qquad\lambda\in\mathbb.\label
$$\(\circ\) Если функция \(\textbf(t)\) дифференцируема при \(t=t_0\) и \(\textbf‘(t_<0>)\neq 0\), то существует \(\displaystyle \lim_<\Delta t\rightarrow 0>\frac<\Delta \textbf><\Delta t>=\textbf‘(t_0)\), и по определению прямая \eqref является касательной к кривой \(\Gamma\) в точке \(M_<0>\). \(\bullet\)В координатной форме уравнение \eqref имеет вид
$$
x=x(t_<0>)+\lambda x'(t_<0>),\quad y=y(t_0)+\lambda y'(t_0),\quad z=z(t_<0>)+\lambda z'(t_<0>),\quad \lambda\in \mathbb,\nonumber
$$
a в канонической форме уравнение касательной записывается в виде
$$
\frac)>)>=\frac)>)>=\frac)>)>.\quad\bullet\nonumber
$$

Понятие гладкой кривой.

Пусть кривая \(\Gamma\) задана уравнением \eqref, где \(\textbf(t)\) — дифференцируемая на отрезке \([\alpha,\beta]\) функция, тогда говорят, что \(\Gamma\) — дифференцируемая кривая.

Если \(r'(t_0)\neq 0\), то точку \(M_<0>\in\Gamma\), где \(\overrightarrow=r(t_0)\), называют неособой точкой кривой \(\Gamma\); если же \(\textbf‘(t_0)=0\), то говорят, что \(M_<0>\) — особая точка кривой \(\Gamma\).

Пусть \(\textbf(t)=(x(t),y(t),z(t))\), тогда \(r'(t_0)=(x'(t_<0>),y'(t_<0>),z'(t_<0>))\), и поэтому точка \(M_0\) является неособой точкой кривой \(\Gamma\) тогда и только тогда, когда \((x'(t_0))^2+(y'(t_0))^2+(z'(t_0))^2 > 0\). из определения неособой точки и утверждения 1 следует, что во всякой неособой точке кривой \(\Gamma\) существует касательная.

Если функция \(r'(t)\) непрерывна на отрезке \([\alpha,\beta]\), то будем говорить, что кривая \(\Gamma\), заданная уравнением \eqref, непрерывно дифференцируема.

Условимся называть кривую гладкой, если она является непрерывно дифференцируемой и не имеет особых точек. Следовательно, кривая \(\Gamma\), заданная уравнением \eqref, является гладкой, если функция \(\textbf‘(t)\neq 0\) при всех \(t\in[\alpha,\beta]\). Если кривая составлена из конечного числа гладких кривых, то такую кривую будем называть кусочно гладкой.

Для непрерывно дифференцируемой кривой \(\Gamma\) в качестве допустимых преобразований параметра (см. замечания выше) рассматриваются функции \(s(t)\), непрерывно дифференцируемые и такие, что \(s'(t) > 0\).

В этом случае на отрезке \([\alpha,\beta]\) определена непрерывно дифференцируемая функция \(t=t(s)\), обратная к функции \(s=s(t)\), причем \(t'(s) > 0\) и выполняется равенство \eqref.

Источник

Что такое гладкая кривая

Педагогические науки/ 5.Современные методы преподавания

Казахский технический университет имени К.И.Сатпаева, г.Алматы

Недифференцируемые функции, представляющие

Определение-1 можно применить лишь для кривых, представленных дифференцируемыми на рассматриваемом промежутке функциями, а для кривых, представленных функциями с бесконечными производными, оно непригодно. Но одна и та же кривая может представляться дифференцируемыми, также и недифференцируемыми отображениями. Примерами последней категории гладких кривых могут быть:

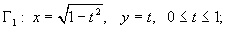
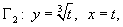
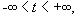
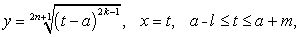
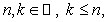
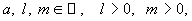
дуга окружности кубическая парабола или любая кривая, представленная в виде и т.д.

По определению-1, такие кривые не относятся к гладким, ибо функции, представляющие их, в указанных промежутках не дифференцируемы.

Для установления гладкости этих, вообще для любой кривой можно воспользоваться следующем определеним ( см. [2] §6.5, там оно приведено в общем виде).

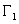
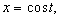
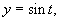
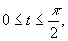
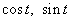
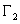
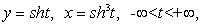
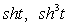
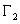
Например, если рассмотренную выше дугу окружности параметризовать в виде: то функции удовлетворят условиям определения-2, следовательно по определению-2, дуга окружности – гладкая; а кубическую параболу можно представить в виде где для функции выполняются все условия определения-2, так что кривая также гладкая.

Мы видим, что хотя кривая первоначально задана недифференцируемыми функциями, но если сможем найти ее подходящие параметрические уравнения с составляющими функциями, удовлетворящими условиям определения-2, то она гладкая. Вот этот процесс параметризации кривой с подходящими свойствами функции и является недостатком определения-2. 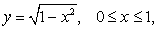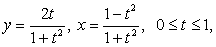Так как способ параметризации одной и той же кривой, не единственный (например, дуга окружности может быть представлена еще и в вид е и т.д. ), то такой подход установления гладкости кривой, явно не рациональный.

1. Основные понятия и терминологии

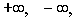
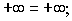
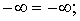
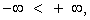
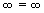
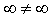
Считаем, что для бесконечностей имеет место со отношения порядка : т.е. бесконечности одного знака равны, а бесконечности разных знаков не равны. Но для бесконечностей без определенных знаков соотношение порядка не распространяется, т.е. выраже ние или не име е т смысла.

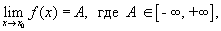
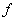
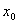
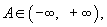
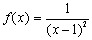
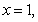
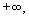
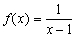
В случае, когда как обычно будем говорить, что « функция в точке имеет предел », а в случае она имеет «конечный предел». Например, функция имеет предел в точке равный а у функции в этой точке предела нет, т.к.

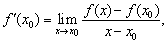
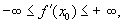
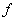
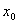
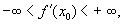
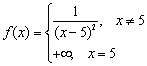
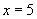
. Аналогично, если имеет место равенство где то « функция в точке имеет производную », а в случае она имеет конечную производную.

Функция непрерывна в точке в широком смысле, ибо

Теперь рассмотрим применение непрерывности функции в широком смысле в решении некоторых вопросов математики.

2. Гладкая кривая и гладкая в широком смысле функция

Аналогическими преимуществами обладает и следующее определение гладкой кривой, заданной явной функцией.

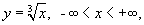
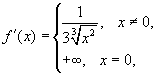
Например, по определению- 2.2 , рассмотренная выше кривая гладкая на любом отрезке, так как производная функции непрерывна в широком смысле в любой точке.

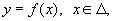
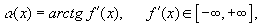
Далее, д ля ф ункции введем понятие ее угловой функции с помощью равенства

(1)

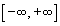
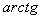
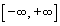
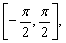
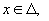
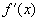
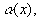
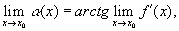
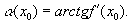
где н епрерывная и монотонная в промежутке функция устан о вливает взаимооднозначное соответствие между расширенным множеством значении производной функций и множеством значении угловой функции так что из существования производной в точке вытекает существование угловой функции в этой точке, и наоборот. Аналогичное утверждение справедливо также для непрерывн ой в широком смысле производной и непрерывно й ( в обычном смысле ) угловой функции ибо имеет место равенство т.е. Поэтому определение- 2.2 будет равносильно следующему определению, сформулированному на языке угловой функции.

О пределение — 2. 3 (на языке угловой функции) . Непрерывная кривая называется гладкой, если имеет непрерывную угл овую функцию на

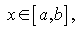
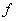
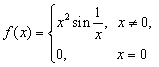
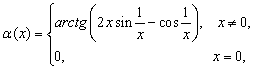
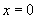
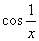
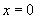
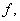
Пример- 1 . Для функции определена угловая функция, равная но она не является непрерывной в точке (функция в точке не имеет предела), и потому кривая, заданная с помощью функции не гладкая на отрезке, содержащем точку

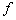
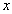
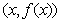
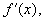
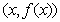
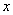
если функция имеет в точке производную, то существует касательная к ее графику в точке с угловым коэффициентом и обратно, если существует касательная в точке графика функции f , то функция имеет в точке производную. Другими словами, для функции f между множеством ее производных и множеством касательных к ее графику можно установить взаимооднозначное соответствие.

Аналогичное утверждение для конечной производной – не верно!

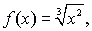
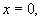
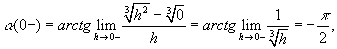
Пример-2. Для функции на отрезке, содержащем точку не существует угловая функция. Действительно,

Следовательно, у этой функции в точке 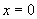не существует ни производная, ни касательная.

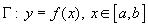
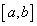
Определение-2.4 (на языке касательной). Непрерывная кривая называется гладкой, если существует непрерывная на отрезке касательная кривой

Введем понятие гладкой в широком смысле функции.

Определение — 2. 5 . Функция f называется гладкой в широком смысле на отрезке 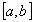, если она имеет непрерывную в широком смысле производную на этом отрезке.

Мы думаем, что понятие непрерывной в широком смысле функции, использованное как инструмент для решения некоторых теоретических проблем математики, может быть также полезным инструментом и в других областях естественных наук по вопросам теоретических и прикладных задач. Поэтому понятия предела, производной, непрерывности функции, определения понятия гладкой кривой и другие вопросы, расмотренные в статье, имели отражения в книге предназначенной для технических вузов.

1. Л.Д.Кудрявцев. Курс математического анализа, т.1, «Высшая школа», 1981.

2. С.М.Никольский. Курс математического анализа, т.1, «Наука», 1983.

Источник