что такое гиперупругий материал

Часть 2: получаем данные по материалам для механики конструкций исходя из результатов измерений

В первой части мы обсудили некоторые факторы, которые следует учитывать при преобразовании ваших результатов измерений характеристик материалов в модель состояния. Мы достаточно подробно рассмотрели гиперупругие материалы. Сегодня мы обсудим способы применения нелинейных упругих и упругопластических материалов, а также изучим метод, позволяющий использовать результаты измерений непосредственно в COMSOL Multiphysics.

Нелинейные упругие материалы

Некоторые материалы проявляют существенную нелинейность уже при малых деформациях. Примерами являются чугун и некоторые керамические материалы. Однако при снятии нагрузки, ведущей к умеренной деформации, они возвращаются в исходное состояние по той же диаграмме деформации, то есть их отклик является упругим. Для описания таких материалов необходима нелинейная упругая модель.

В предыдущей публикации блога мы обсудили гиперупругие материалы. Почему бы не воспользоваться одной из таких моделей, чтобы обеспечить соответствие с диаграммой деформации, построенной на основе результатов измерений, для, например, мелкозернистого чугуна? Проблема в том, что модели гиперупругих материалов рассчитаны на большие деформации. Для эластомеров растяжение может достигать сотен процентов от исходной длины, тогда как область упругих деформаций для металлов и более хрупких материалов составляет обычно менее 1%.

Например, крайне популярная модель Муни — Ривлина является существенно линейной при малых деформациях. Поэтому для нашей задачи она не подходит. В модели Огдена напряжение вычисляется как сумма значений растяжения, возведенных в определенные степени. Однако для малых деформаций растяжение может быть ограничено значениями порядка 0.999 — 1.001. Чтобы модель отражала существенную нелинейность материала, показатель степени в формуле должен быть чрезвычайно большим. Данные измерений вряд ли будут хорошо соответствовать такому закону. Для хрупких материалов более естественной характеристикой деформации является техническая деформация. О различных величинах, используемых для измерения напряжений и деформаций, можно прочитать в публикации «Why All These Stresses and Strains?»

Для решения этой задачи COMSOL предлагает набор нелинейных упругих моделей, рассчитанных на малые деформации. Для работы этих моделей материалов необходим модуль Nonlinear Structural Materials (Нелинейные конструкционные материалы) или Geomechanics (Геомеханика). Эти модели доступны в интерфейсах Solid Mechanics (Механика твердого тела) и Membrane (Мембрана). Рассмотрим способы применения этих материалов.

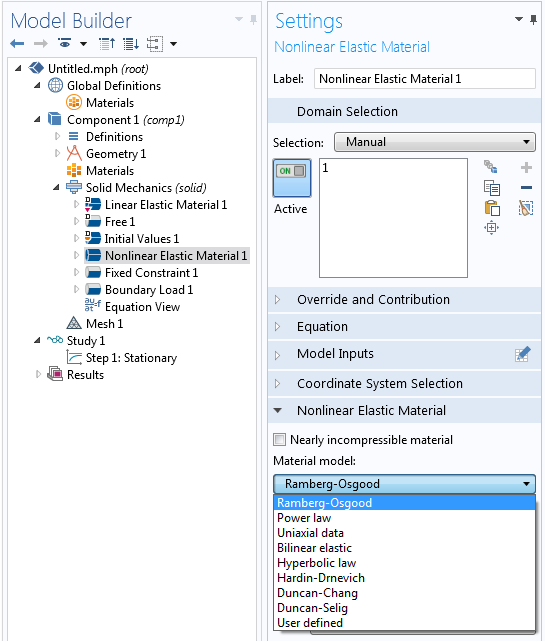
Выбор модели нелинейного упругого материала в COMSOL Multiphysics.

Всего доступно девять моделей нелинейных упругих материалов. Некоторые из них представляются в виде простой математической формулы с небольшим количеством параметров. Одна из этих моделей материалов является особенно полезной при обработке экспериментальных данных о зависимости деформации от напряжения: Uniaxial data (Однонаправленные данные). Эта модель предназначена именно для анализа на основе результатов измерений. Рассмотрим настройки этой модели:

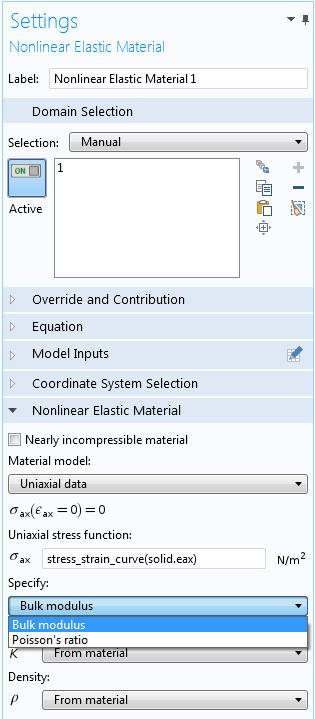
Настройки нелинейной упругой модели Однонаправленные данные.

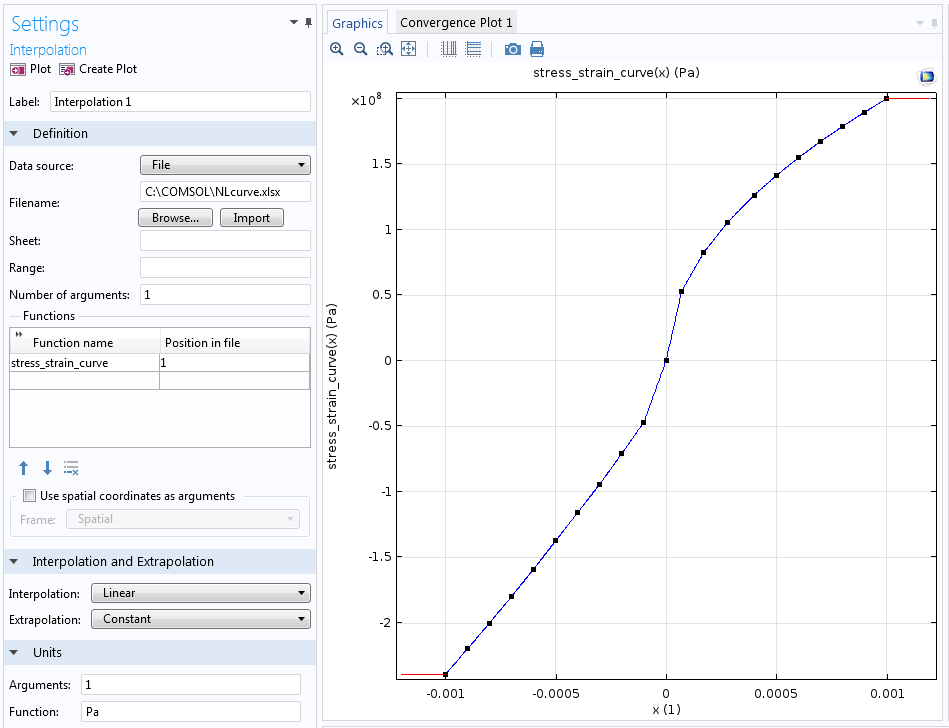
Импортированная диаграмма зависимости однонаправленной деформации от однонаправленного напряжения.

Однако эта кривая для однонаправленных характеристик не содержит достаточной информации для того, чтобы полностью определить многонаправленный основной закон. Необходимо сделать еще одно предположение. Вам требуется задать либо постоянную величину коэффициента Пуассона, либо модуль объемной упругости. Для многих материалов хорошим приближением является постоянный коэффициент Пуассона в диапазоне от 0,2 до 0,3. Это все, что нужно для построения полной модели материала.

Обратите внимание на диаграмму деформации выше: кривые для растяжения и сжатия не совпадают. Однако при многонаправленном напряжении определенная точка материала может испытывать натяжение в одном направлении и сжатие в другом. Какую ветвь кривой для материала следует применять в таком случае? Модель материала является изотропной: она обладает одинаковой жесткостью во всех направлениях. Однако определяющей характеристикой является изменение объема. Если локальное изменение объема отрицательно, то применяется ветвь, характеризующая сжатие.

Примечания: теория

Существование изотропного нелинейного упругого материала теоретически возможно только при соблюдении следующих условий:

Если эти условия не выполняются, то можно создать нагрузочный цикл, который будет прэнергию, то естьвечный двигатель.

Все встроенные материалы разрабатывались так, чтобы соответствовать этим условиям. Рассмотрим, например, настройки для Двухлинейного упругого материала (Bilinear elastic material). В них вам необходимо указать модули объемной упругости для растяжения и сжатия — не модули Юнга, как можно было ожидать.

Чаще всего специалисты по расчету строительных конструкций имеют дело с модулем Юнга и коэффициентом Пуассона. Это основные характеристики упругого материала. Однако, в соответствии с требованиями выше, если модуль Юнга зависит от деформации, то…

Как тогда можно задать однонаправленные данные при постоянном коэффициенте Пуассона? Для решения этой задачи мы разработали скрытые от пользователя допустимые функции для модуля объемной упругости и модуля поперечной упругости. Модуль Юнга при этом не используется, хотя при взгляде на график этого можно было ожидать.

При этом я видел несколько успешных моделей, в которых аналитик добавил зависимости деформации в модулях Юнга для изотропных или ортотропных материалов в модели упругого материала. Для решения прикладных задач такой метод может подойти. Учебное приложение Modeling Stress-Dependent Elasticity является примером определения зависимого от напряжения модуля Юнга. Чтобы такой подход работал, необходимо, чтобы структура подвергалась преимущественно пропорциональному нагружению (т. е. без поворота направлений главных деформаций).

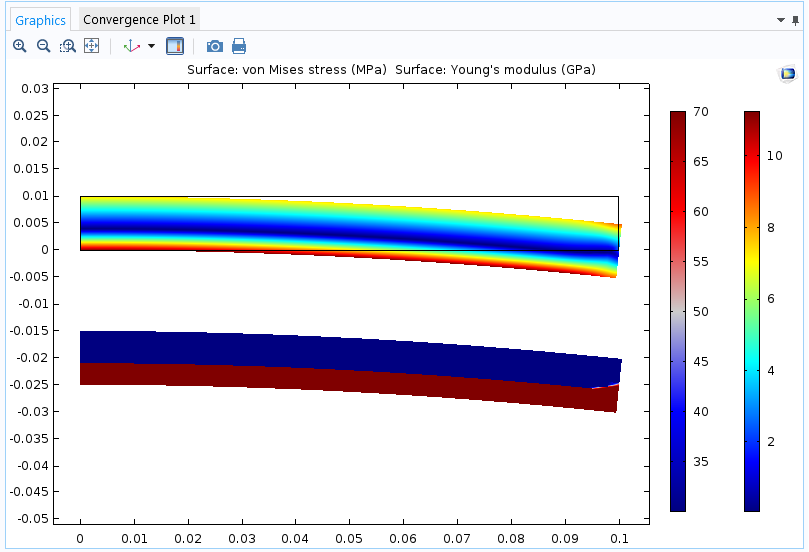
Консольная балка с различными значениями модуля Юнга для растяжения и сжатия. Свободный конец балки подвергается изгибному моменту. На верхнем графике показано напряжение по Мизесу, на нижнем — текущее значение модуля Юнга.

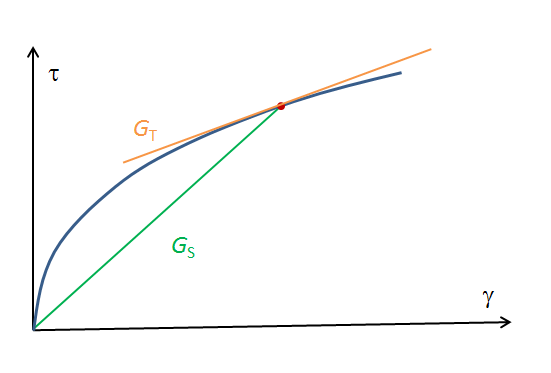
Когда вы задаете для модели свойство нелинейной упругости при помощи встроенных моделей или собственных выражений, важно сохранять строгое разделение между тангенциальной жесткостью и секущей жесткостью. Выражение для нелинейной упругой модели часто похоже на формулу для линейной модели, но с зависимостью коэффициента упругости (который уже не является константой!) от напряжения или деформации. Предположим, что напряжение сдвига \tau связано с деформацией сдвига \gamma как

В таком случае модуль сдвига G_S(\gamma) является секущим модулем сдвига. Произведение полной деформации на секущий модуль дает полное напряжение. С другой стороны, тангенциальным модулем сдвига G_T(\gamma) называется жесткость, проявляемая при малых изменениях деформации, как показано на рисунке ниже.

Математическая зависимость между двумя модулями:

Обычно результаты измерений представляются в форме

Это означает, что секущая жесткость представляется в виде

При преобразовании диаграммы деформации в форму секущей с помощью этого выражения необходимо избегать возможного деления на ноль при нулевой деформации.

Кроме того, иногда вы можете столкнуться с утверждением, что свойства определенного материала описываются степенной зависимостью при определенном показателе степени
n. Это может означать, что

Модель Степенная зависимость (Power law) в COMSOL Multiphysics основана на первом, более распространенном определении, в котором показатель степени для деформации n связан с наклоном кривой на диаграмме деформации, построенной в полулогарифмических координатах.

Аппроксимация пластичности с помощью нелинейной упругости

Эксперимент на чистое растяжение не позволяет определить, обусловлена ли нелинейность определенных результатов измерений пластичностью. Необходимо также проанализировать кривую разгрузки. Иллюстрацией к этому утверждению служит анимация ниже из предыдущей публикации в блоге.

Применение нелинейной модели упругости для моделирования пластичности рассматривалось в предыдущей публикации в блоге.

Нелинейная модель упругого материала Рамберга— Осгуда, как и модель однонаправленных данных, создавалась в качестве простой замены полной упругопластической модели. Применение нелинейного упругого материала значительно менее требовательно к компьютерным ресурсом. Но каковы ограничения такого подхода?

Заключение

При выборе подходящей модели материала необходимо учитывать общую точность анализа. При решении инженерных задач часто приходится пользоваться неполной информацией: данным о нагрузках, однородности материалов и размерам структуры обычна присуща некоторая неопределенность. Выбор граничных условий также является аппроксимацией. В этой цепочке качество результатов определяется самым слабым звеном, и таким звеном не всегда является точный математический фундамент модели материала.

В предыдущей публикации в блоге я писал, что не стоит просто вводить диаграмму деформаций напрямую.

Почему же сегодня я поступил иначе? Дело в том, что при работе с моделью однонаправленных данных используются фактические результаты измерений. Для всех гиперупругих моделей, а также большей части других нелинейных упругих моделей, под результаты измерений необходимо подогнать математическую модель с малым количеством параметров. Безопасно выполнить такую подгонку возможно только при участии человека.

Источник

Подгонка параметров различных моделей гиперупругих материалов для соответствия экспериментальным данным

Ранее в блоге мы обсудили необходимость получения специальным образом измеренных данных, чтобы подогнать параметры соответствующей модели среды. Мы рассмотрели также типичные экспериментальные методы и условия их проведения, которые необходимо учитывать при выборе модели среды, и привели пример использования результатов измерения непосредственно в модели нелинейной упругой среды. Сегодня мы сконцентрируемся на том, как подобрать параметры в различных моделях гиперупругих материалов таким образом, чтобы наилучшим образом описать полученные экспериментальные данные.

Метод подгонки в среде COMSOL Multiphysics

Следующим вопросом, после получения результатов измерения является: каким образом из них можно получить параметры, требуемые (необходимые) для описания модели гиперупругой среды? Один из возможных способов, используемых в среде COMSOL Multiphysics — это подгонка параметризованной аналитической функции к экспериментально измеренным результатам с помощью Модуля Оптимизации.

В следующем разделе, мы определим аналитические выражения, связывающие тензоры напряжений и деформации, для двух обычно проводимых тестов — одноосного и равномерного двуосного — растяжения вдоль одной оси и равномерного растяжения по двум осям одновременно. Затем мы используем эти аналитические выражения для подгонки к результатам измерений с целью получения параметров среды.

Изотропная, почти несжимаемая гиперупругая среда (гиперупругость)

Точное описание объемной деформации гиперупругих материалов для оценки материальных параметров среды является очень громоздкой процедурой. Зачастую вместо этого, предполагается полная несжимаемость среды и выполняется оценка нужных параметров с помощью подгонки. После этой оценки подбирается правдоподобное значение модуля объемного сжатия почти несжимаемого гиперупругого материала, так как это значение не вычисляется.

В этой статье, измеренные данные будут использоваться для подгонки параметров нескольких моделей полностью несжимаемых гиперупругих материалов. Начнем с обзора некоторых базовых концепций, лежащих в основе понятия почти несжимаемой среды, а затем охарактеризуем процесс измерения напряжений для случая полной несжимаемости.

Для почти несжимаемой гиперупругой среды, полная плотность энергии деформации представляется в виде

где W_ и W_ — изохорная и объемная плотности энергии деформации, соответственно. Второй тензор напряжений Пиола-Кирхгофа определяется выражением

где p_

— объемное напряжение, J — относительное изменение объема, и C — правый тензор Коши-Грина.

Разложим второй член этого уравнения, так что второй тензор напряжения Пиола-Кирхгофа будет равен

где \bar_ <1>и \bar_ <2>— инварианты изохорного правого тензора Коши-Грина \bar = J^<-2/3>C

Здесь F — градиент деформации.

Замечание: Более подробное описание измерений различных напряжений можно найти в предыдущей статье нашего блога “Why All These Stresses and Strains?“

где \lambda_a обозначает главные значения растяжений. Это позволяет выразить главные значения второго тензора напряжений Пиолы-Кирхгофа через главные значения растяжений (в виде функции от главных значений растяжений)

Рассмотрим теперь эксперименты одно- и двухосного растяжения/сжатия, описанные в первой статье нашего блога из серии «Конструкционные Материалы». Для обоих этих материальных тестов можно получить общее соотношение между напряжением и растяжением.

В предположении несжимаемости ( J=1 ) главные растяжения для одноосной деформации изотропного гиперупругого материала определяются значениями

Градиент деформации запишется в виде

Для одноосного растяжения S_2 = S_3 = 0 объемное напряжение p_

можно исключить, тогда

Изохорные инварианты \bar_<1_> и \bar_<2_> могут быть выражены через главное растяжение \lambda как

В предположении несжимаемости главные значения растяжений для равномерной двухосной деформации изотропного гиперупругого материала определяются соотношениями

Для равномерного двухосного растяжения S_3 = 0 объемное напряжение p_

можно исключить, тогда

Инварианты \bar_<1_> и \bar_<2_> тогда даются выражениями

Зависимость напряжения от главных значений растяжения в моделях несжимаемых гиперупругих материалов

Рассмотрим соотношения между напряжением и растяжением для нескольких наиболее распространенных моделей гиперупругих материалов. Для подгонки параметров моделей будет применяться первый тензор напряжений Пиолы-Кирхгофа.

Модель Нео-Хукена (Neo-Hookean)

Полная плотность энергии деформации в модели среды Нео-Хукена дается выражением

где J_ — относительное изменение упругого объема, \mu — материальный параметр, который нужно вычислить с помощью численной подгонки. При условии полной несжимаемости, используя уравнения (1) и (2), выражения первого напряжения Пиолы-Кирхгофа для случаев одноосной и равномерной двухосной деформации преобразуются к виду

Зависимость напряжения от растяжения для некоторых других моделей гиперупругих материалов приводятся ниже. Они легко могут быть получены с помощью уравнений (1) и (2), которые связывают напряжение и плотность энергии деформации.

Модель Муни-Ривлина (Mooney-Rivlin) с двумя параметрами

Здесь C_ <10>и C_ <01>— материальные параметры Муни-Ривлина.

Модель Муни-Ривлина, пять параметров

Здесь C_ <10>, C_ <01>, C_ <20>, C_ <02>, и C_ <11>— материальные параметры Муни-Ривлина.

Модель Арруда-Бойса (Arruda-Boyce)

Здесь \mu_0 и N — материальные параметры Арруда-Бойса, и c_p — пять первых членов разложения в ряд Тейлора обратной функции Ланжевена.

Модель Йо (Yeoh)

Здесь значения c_p — материальные параметры Yeoh.

Модель Огдена (Ogden)

Здесь \mu_p и \alpha_p — материальные параметры Огдена.

Численная подгонка в программной среде COMSOL Multiphysics с помощью интерфейса Оптимизации

Используя интерфейс Оптимизации в среде COMSOL Multiphysics, мы будем подгонять теоретическую кривую, рассчитываемую с помощью аналитических выражений, детально описанных выше, к экспериментально измеренной зависимости напряжения от растяжения. Отметим, что используемые здесь экспериментальные данные — это номинальное напряжение, которое определяется как сила в текущей конфигурации, действующая на первоначальную (недеформированную) площадь образца. Очень важно, чтобы численные и измеренные данные, используемые в подгонке, соответствовали друг другу. Следовательно, для подгонки к измеренным данным будут применяться аналитические выражения для первого тензора напряжений Пиолы-Кирхгофа. График ниже показывает измеренные значения номинального напряжения (необработанные данные) при одноосном и равномерном двухосном растяжении вулканизированной резины.

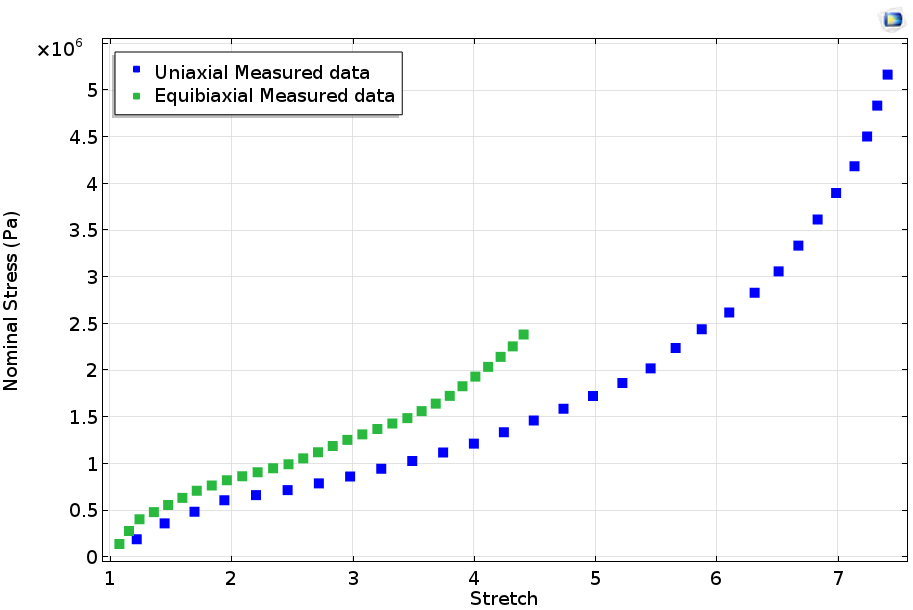
Измеренная зависимость напряжение-деформация, из статьи Treloar.

Начнем с настройки модели Нео-Хукена для подгонки результатов одноосного эксперимента. Первым шагом является добавление интерфейса Оптимизация к 0D модели. Здесь 0D подразумевает, что наш анализ не привязан к конкретной геометрии.

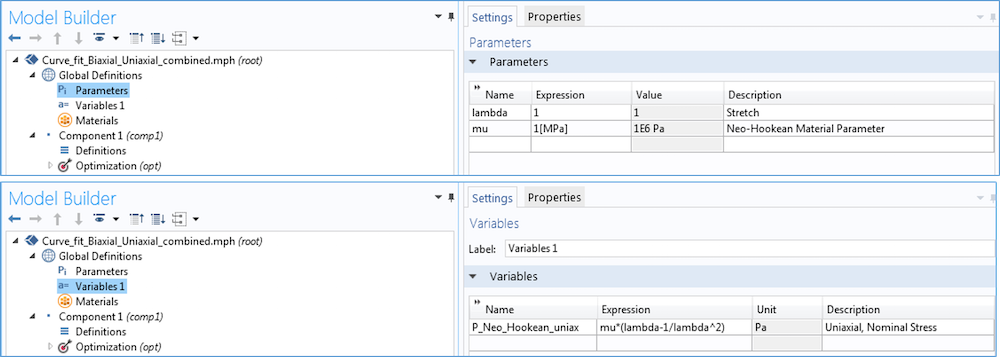
Затем можно определить материальные параметры, которые необходимо вычислить, и переменные для аналитической зависимости напряжения от растяжения. На картинке ниже показан выбор параметров и переменной, определяемых для случая одноосного растяжения в материальной модели Нео-Хукена.

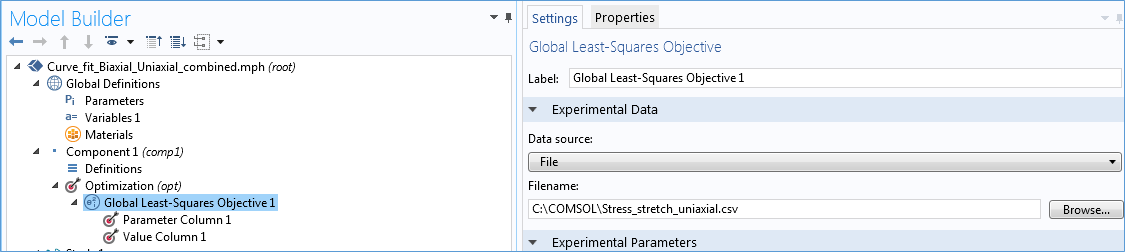
Внутри интерфейса Оптимизация, имеется раздел Глобальный объект метода наименьших квадратов (Global Least-Squares Objective), в котором можно указать входной файл с измеренной в одноосном эксперименте зависимостью напряжение—деформация. Далее имеются пункты Столбец параметров (Parameter Column) и Столбец значений (Value Column). Здесь в качестве измеряемого параметра задается лямбда (растяжение) и указывается аналитическое выражение зависимости напряжение—деформация для одноосного растяжения, которое будет использоваться для подгонки к измеренным данным. Можно также указать весовой множитель в пункте Столбец весовых коэффициентов (Column contribution weight). Более подробная информация о параметрах раздела Глобальный объект метода наименьших квадратов (Global Least-Squares Objective) доступна в учебном приложении Численная подгонка модели Муни-Ривлина (Mooney-Rivlin Curve Fit tutorial), расположенном в нашей Галерее приложений.

Теперь мы готовы к тому, чтобы решить вышеуказанную задачу, а именно, оценить материальные параметры с помощью подгонки результатов эксперимента по одноосному растяжению в рамках модели Нео-Хукена. Однако вряд ли это будет хорошей идеей. В первой части блог-серии объясняется, что этот, казалось бы, простой тест имеет слишком много неучтенных факторов параметров. Ниже мы продемонстрируем последствия калибровки материала, основанные только на одном наборе входных данных.

В зависимости от условий эксперимента лучшую оценку материальных параметров можно получить, используя комбинации различных измерительных методов: одноосное растяжение/сжатие, двухосное растяжение, кручение и т.д. Собранные таким образом данные можно использовать для подгонки, представив напряжение в аналитическом виде в каждом из рассматриваемых случаев.

В этой статье совместно используются результаты экспериментов по одноосному и равномерному двухосному растяжению исследуемого образца. Точно так же, как мы настраивали модель оптимизации для одноосного теста, определим другую процедуру глобальной минимизации для равномерного двухосного теста, а также сопутствующие ей параметры и значения. Во второй процедуре глобальной минимизации укажем в качестве входных данных файл с результатами измерений напряжение-деформация двухосного эксперимента. В столбце значений выберем аналитическое выражение для напряжения в двухосном эксперименте, которое будет использоваться для подгонки по измеренным данным.

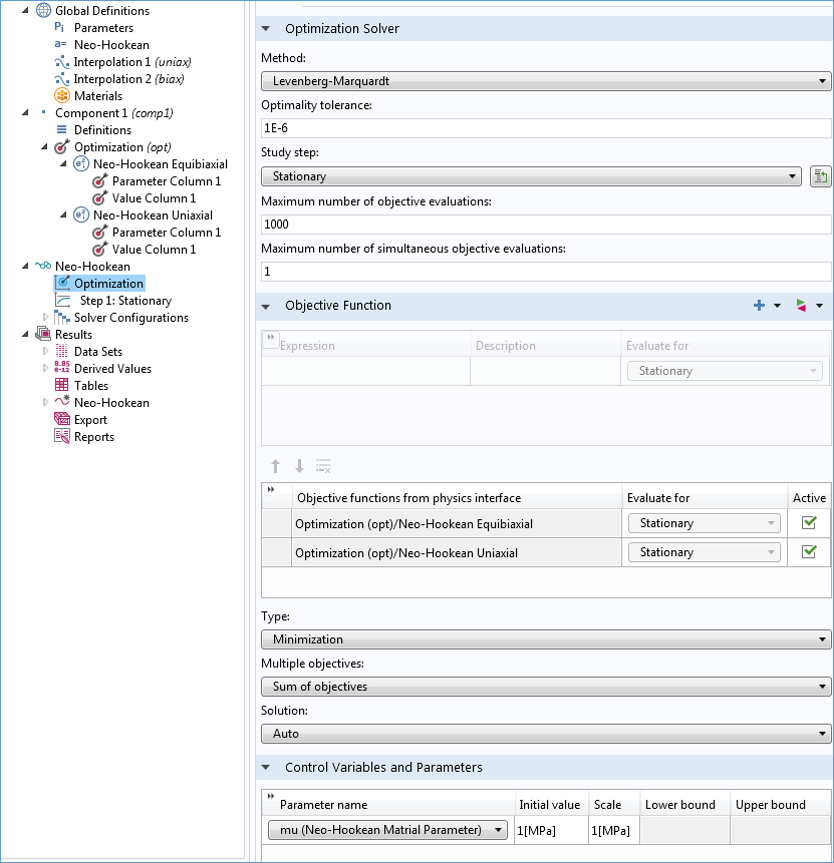
Настройки для шага Оптимизации приведены на изображении ниже. Разделы в древовидном каталоге переименованы вручную, чтобы отразить используемую модель (Нео-Хукен) и два набора экспериментальных данных (одноосный и равномерный двухосный тесты). Алгоритмом оптимизации является метод Левенберга-Марквардта (Levenberg-Marquardt), который используется для решения задач методом наименьших квадратов. Теперь модель настроена таким образом, чтобы оптимизировать поиск глобального минимума по двум наборам данных — одноосного и двухосного экспериментов.

График ниже представляет результат сравнения смоделированных и измеренных данных. Равные весовые множители присваивались обоим наборам экспериментальных данных (одноосному и двухосному) для подгонки методом наименьших квадратов. Очевидно, что модель Нео-Хукена со всего лишь одним регулируемым параметром не может обеспечить должного соответствия экспериментальным данным, которые являются нелинейными и имеют одну точку перегиба.

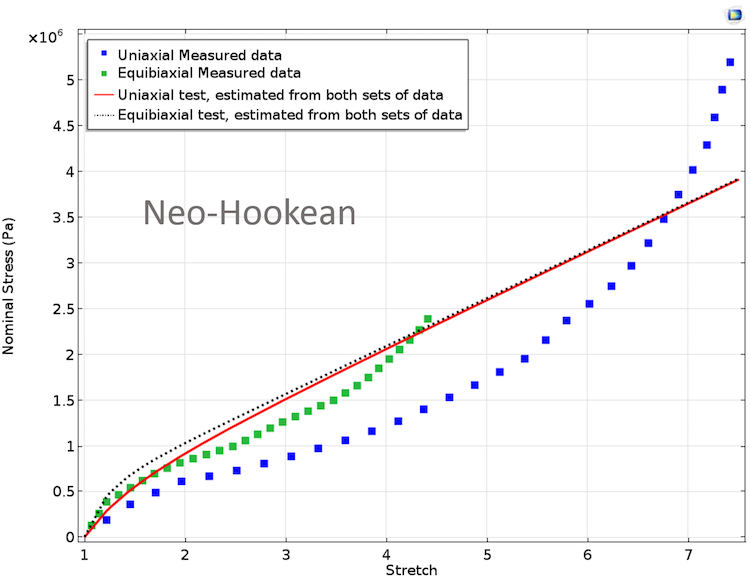
Подгонка материальных параметров в модели Нео-Хукена. Равные весовые множители присваивались обоим наборам экспериментальных данных.

Подгонка кривых с неравными весовыми множителями для двух тестовых наборов данных приведет к незначительному изменению подгоняемых кривых. Подобно модели Нео-Хукена настроим процедуру оптимизации по методу наименьших квадратов, соответствующую моделям гиперупругих материалов Муни-Ривлина, Арруда-Бойса, Йо и Огдена. В вычислениях, представленных ниже, мы включим в рассмотрение оба случая равных и неравных весовых множителей.

В случае неодинаковых весов, больший, но произвольным образом выбранный множитель будет использоваться для полного набора данных двухосного эксперимента. Принципиально можно присвоить неравные веса только для некоторого диапазона значений относительных растяжений вместо полного набора данных. В этом частном случае нужно разделить входные данные на части, используя отдельные разделы Глобальный объект метода наименьших квадратов (Global Least-Squares Objective) для каждого диапазона значений растяжения. Это позволит корректировать весовые множители в различных диапазонах значений растяжения.

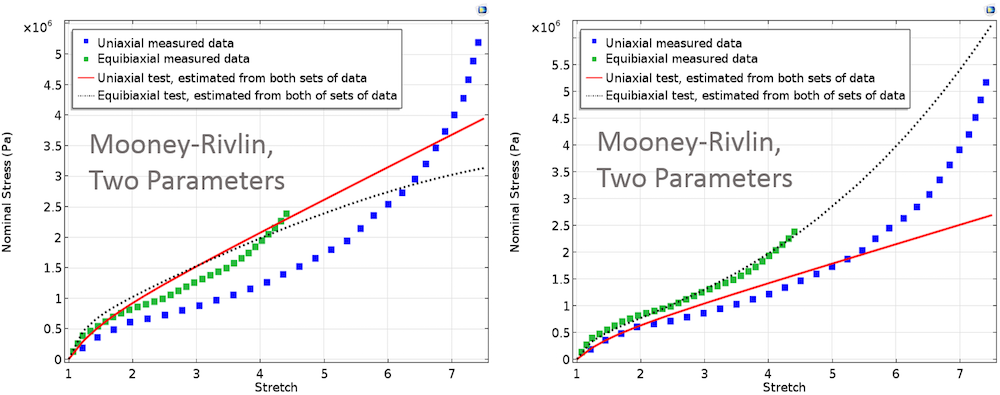
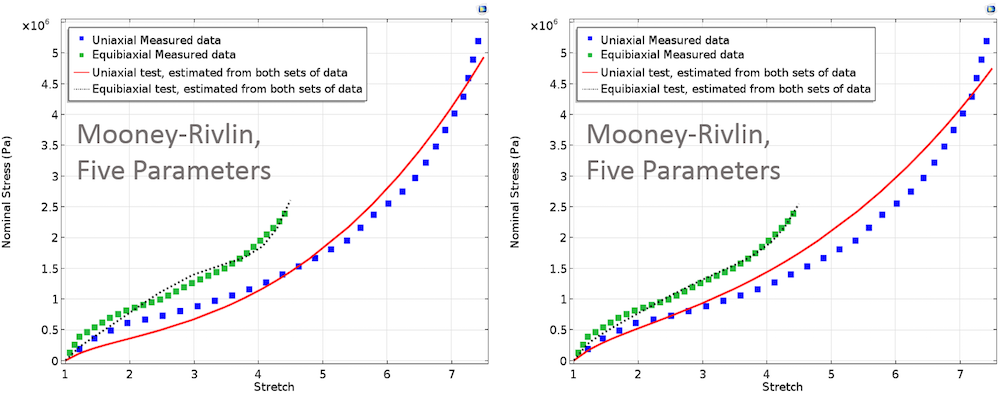
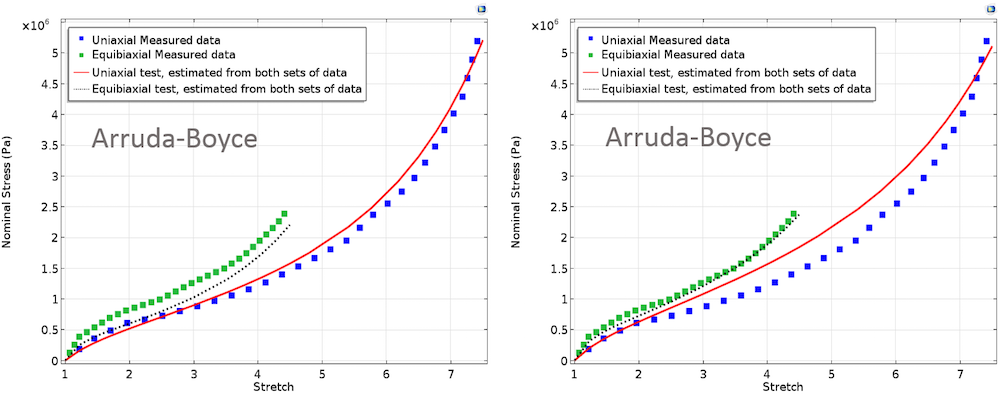
Нижеследующие графики представляют кривые подгонки для различных материальных моделей с равными и неравными весовыми множителями и соответствуют двум тестовым экспериментам.

Слева: Кривые подгонки, полученные в рамках моделей Муни-Ривлина, Арруда-Бойса и Йо. В этом случае, одинаковые весовые множители присваивались обоим наборам экспериментальных данных. Справа: Кривые подгонки, полученные в рамках моделей Муни-Ривлина, Арруда-Бойса и Йо. Здесь, более высокий вес присваивался данным двухосного эксперимента.

Модель Огдена с тремя слагаемыми очень хорошо описывает оба набора экспериментальных данных в случае, когда им присвоены равные весовые множители.

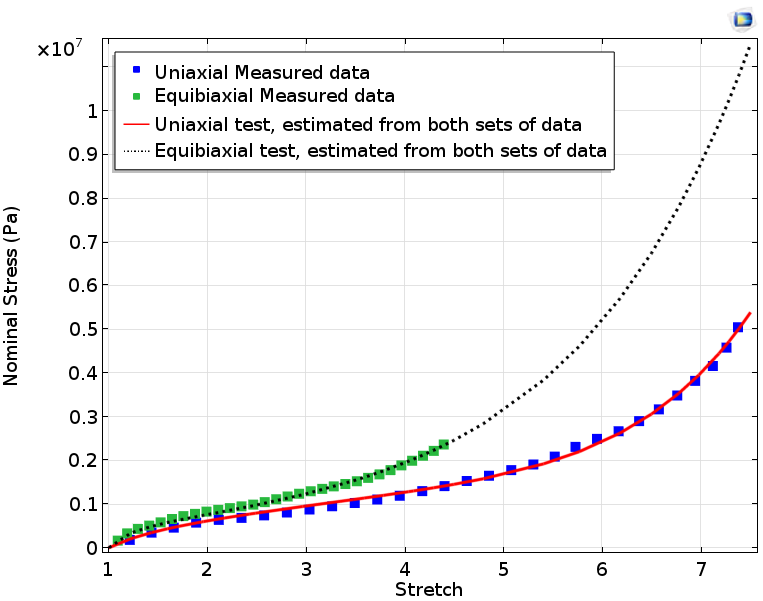
Кривые подгонки, полученные в рамках модели Огдена с тремя слагаемыми.

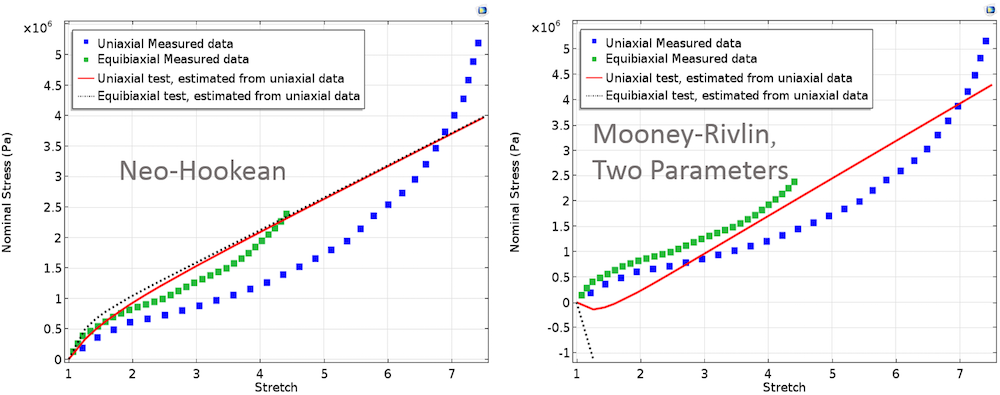
В случае, когда подгонка осуществляется только с одноосным набором данных, а затем вычисленные значения параметров используются в расчете графической зависимости для двухосного эксперимента, мы получим результаты, графически представленные ниже. Эти графики демонстрируют полное несоответствие расчетных и измеренных зависимостей для равномерного двухосного растяжения образца. При оценке материальных параметров лучше всего выполнять подгонку с комбинированным набором данных, полученных в различных режимах деформации, и избегать использования данных только одной деформационной моды.

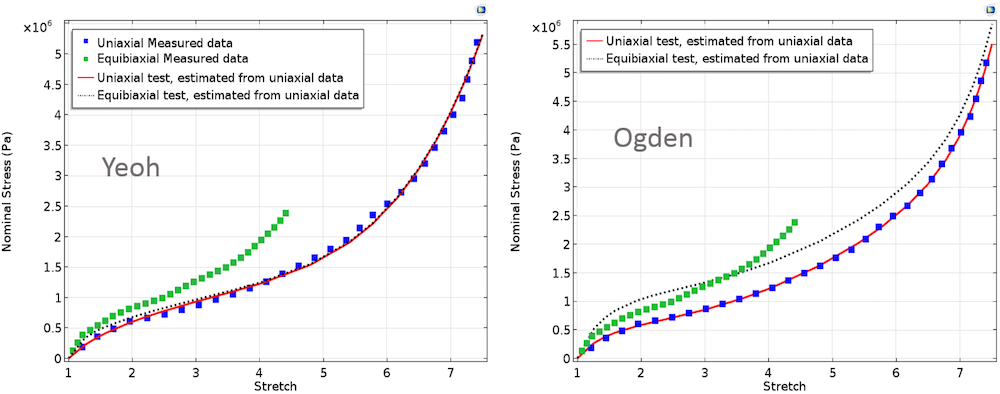
Одноосное и двухосное напряжения, вычисленные подгонкой модельных параметров с использованием данных только одноосного эксперимента.

Заключительные замечания

Определение материальных параметров для моделей гиперупругих сред с помощью подгонки аналитических кривых может показаться надежным методом. Однако необходимо также учитывать устоячивость данной модели гиперупругого материала. Критерий для определения устойчивости известен как устойчивость по Друкеру (Drucker stability). Согласно критерию Друкера, приращение работы, вызванное соответствующим приращением напряжения, всегда должно быть больше нуля. Если критерий нарушается, модель материала будет неустойчивой.

В этой блог-статье мы продемонстрировали, как можно использовать интерфейс Оптимизации (Optimization) в среде COMSOL Multiphysics для подгонки аналитических кривых ко множественному набору экспериментальных данных. Альтернативный способ подгонки, который не требует интерфейса Оптимизации также являлся темой обсуждения в более ранней блог-статье. Аналогично тому, как мы использовали здесь данные одноосного и двухосного растяжения образца для оценки материальных параметров, можно выполнять подгонку экспериментальных данных, полученных с помощью сдвиговых и объемных тестов, для характеристики других состояний деформации.

Для более подробных пошаговых инструкций о том, как использовать интерфейс Оптимизации для подгонки кривых, ознакомьтесь с учебным приложением Численная подгонка модели Муни-Ривлина (Mooney-Rivlin Curve Fit tutorial) в нашей Галерее приложений.

Источник