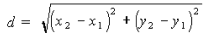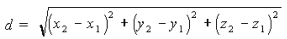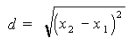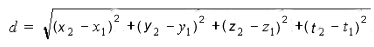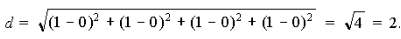что такое гиперкуб во вселенной

Что такое тессеракт? Четырехмерный объект, который невозможно построить

Давайте попробуем понять четвертое измерение. В геометрии четырехмерный аналог куба называется тессерактом. Его легко экстраполировать, рассматривая более низкие измерения.

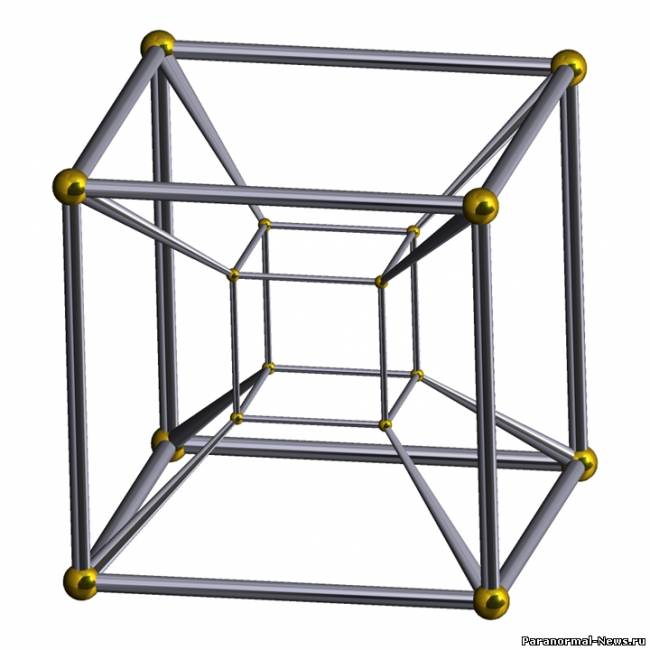
Аналогично, четырехмерный куб (также известный как гиперкуб или тессеракт) имеет 16 вершин. Он может быть создан путем сгущения куба в четвертом измерении. Но поскольку мы живем в трехмерном мире, построить четырехмерный объект невозможно.

В целом можно сказать, что тессеракт относится к кубу так же, как куб относится к квадрату. У него 24 грани, 32 ребра и 16 вершин.

Объект, меняющий размеры, от точки до тессеракта

Тессеракт очень трудно визуализировать

Визуализировать тессеракт или любой другой четырехмерный объект чрезвычайно трудно, если вообще возможно. Это происходит потому, что наше воображение недостаточно сильно, чтобы спроецировать наше сознание в искусственный мир, который сильно отличается от нашего собственного.

Наш мозг устроен так, чтобы преобразовывать двухмерные данные в трехмерное представление. Точнее, наши глаза посылают в мозг пару двухмерных изображений, из которых мозг строит двухмерную+глубинную модель поля зрения.

Это то, о чем наш мозг лучше всего приспособлен думать. Трехмерное пространство легко визуализировать, потому что мы буквально видим его все время. Однако у нас нет прямого опыта более высоких измерений, и поэтому у людей нет четкого прототипа, который можно было бы использовать в качестве трамплина для их визуализации.

С другой стороны, физики и математики, имеющие опыт работы с более высокоразмерными пространствами, более способны, чем остальные, визуализировать их в своем мозгу.

Давайте попробуем визуализировать тессеракт

Как куб можно спроецировать в двухмерное пространство, так и тессеракт можно спроецировать в трехмерное пространство.

Рисунок 2

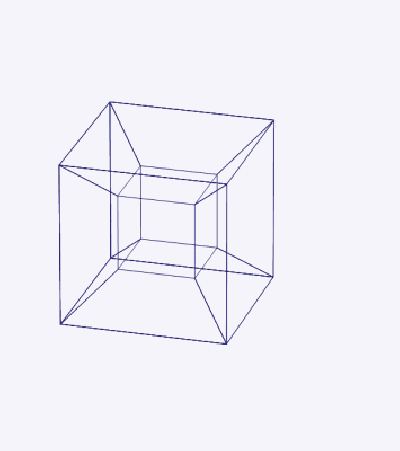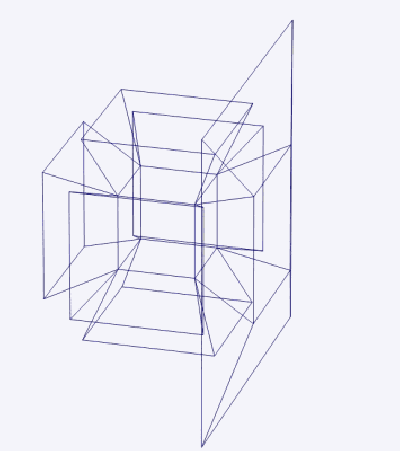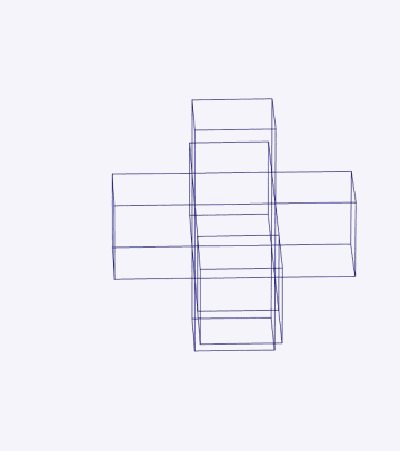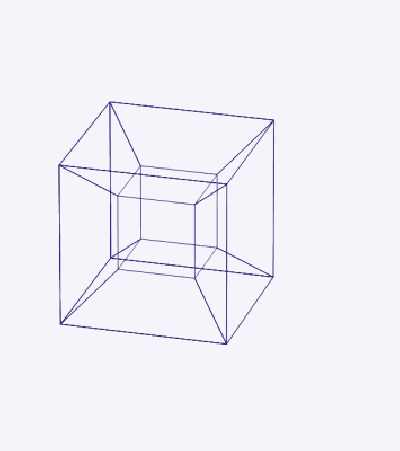
Поверхность трехмерного куба содержит 6 квадратных граней; аналогично гиперповерхность тессеракта содержит 8 кубических ячеек.

Тессеракт можно развернуть на 8 кубиков в трехмерном пространстве (рис. 2). Это похоже на развертывание куба на 6 квадратов в двумерном пространстве. Разворачивание геометрического объекта [с плоскими сторонами] называется сеткой. В тессеракте 261 сетка.

Существует два типа четырехмерных вращений:

1) Простые вращения: трехмерная проекция Тессеракта (рис. 3), выполняющая простое вращение вокруг плоскости, разделяющей пополам фигуру сверху вниз и спереди слева направо.

Рисунок 3 | Альтернативная проекция тессеракта

2) Двойное вращение: трехмерная проекция тессеракта (рис. 4), показывающая двойное вращение вокруг двух ортогональных плоскостей.

Рисунок 4 | Альтернативная проекция тессеракта

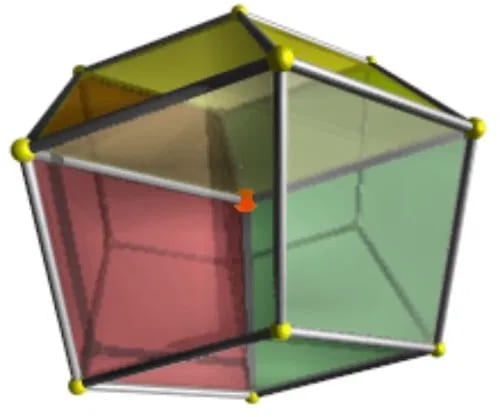
Тессеракт также может быть показан с точки зрения устранения скрытого объема. На рисунке 5, например, красная грань находится ближе всего к четвертому измерению и имеет четыре кубические ячейки, расположенные вокруг нее.

Рисунок 5 | Тессеракт с точки зрения устранения скрытого объема

Тессеракт был открыт в 1888 году

Слово «тессеракт» было придумано британским математиком и писателем-фантастом Чарльзом Говардом Хинтоном. Он впервые использовал это слово в 1888 году в своей книге «Новая эра мышления». Он также придумал несколько новых слов для описания элементов в четвертом измерении.

С тех пор слово «тессеракт» используется в различных видах искусства, архитектуры и научно-фантастических историях (таких, как «Мстители» и «Агенты «Щ.И.Т.»»), где оно не имеет ничего общего с четырехмерным гиперкубом.

Последние исследования

Пространственные представления человека не ограничены трехмерным миром

Группа исследователей из Университета Иллинойса, США, провела исследование, чтобы выяснить, может ли человек развить интуитивное понимание четырехмерного пространства. Для получения точных результатов они использовали виртуальную реальность (VR).

Данные показывают, что люди, не имеющие специальной практики, могут научиться делать пространственные суждения о длине и угле между линейными сегментами, встроенными в четырехмерное пространство, просматриваемое в виртуальной реальности. Их суждение включало данные как трехмерной проекции, так и четвертого измерения. Основные представления были основаны на визуальных образах (установленных алгебраической природы), хотя и примитивных и недолговечных.

Общее число возможных измерений во Вселенной

В то время как общая теория относительности рисует картину четырехмерной Вселенной, теория суперструн утверждает, что она имеет 10 измерений, а расширенная версия, называемая М-теорией, утверждает, что она имеет 11 измерений. В бозонической теории струн пространственное время 26-мерно. Эти теории просто представляют собой математические уравнения. Они настолько сложны, что никто не знает их точной формы.

Эксперимент по изучению теоретических материалов в четырехмерном пространстве

Международная группа исследователей смогла разработать двумерную экспериментальную систему, которая позволяет им анализировать физические свойства «материалов», которые теоретически существуют только в четырехмерном пространстве.

Более конкретно, они продемонстрировали, что четырехмерные квантовые эффекты Холла могут быть эмулированы с помощью фотонов, проходящих через двумерный волноводный массив.

Как эти исследования могут быть полезны в нашем трехмерном мире? Скажем, квазикристаллы (широко используемые для покрытия некоторых антипригарных сковородок), как было показано, имеют скрытые измерения. Этот эксперимент может помочь нам понять физику этого скрытого измерения. Затем эта физика может быть использована в качестве принципа проектирования нового фотонного оборудования.

Источник

Учения о многомерных пространствах начали появляться в середине XIX века. Идею четырехмерного пространства у ученых позаимствовали фантасты. В своих произведениях они поведали миру об удивительных чудесах четвертого измерения.

Герои их произведений, используя свойства четырехмерного пространства, могли съесть содержимое яйца, не повредив скорлупы, выпить напиток, не вскрывая пробку бутылки. Похитители извлекали сокровища из сейфа через четвертое измерение. Хирурги выполняли операции над внутренними органами, не разрезая ткани тела пациента.

Каждая пара непараллельных трёхмерных граней пересекается, образуя двумерные грани (квадраты), и так далее. Окончательно, тессеракт обладает 8 трёхмерными гранями, 24 двумерными, 32 рёбрами и 16 вершинами.
Кстати согласно Оксфордскому словарю, слово tesseract было придумано и начало использоваться в 1888 Чарльзом Говардом Хинтоном (1853—1907) в его книге «Новая эра мысли». Позже некоторые люди назвали ту же самую фигуру тетракубом (греч. тетра — четыре) — четырёхмерным кубом.

Построение и описание

Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трёхмерного пространства.
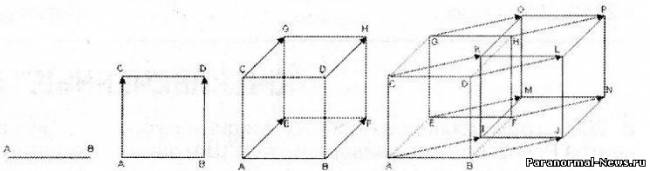
В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L. На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAGHFE. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.

Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб.

Возьмём проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями — боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» — трёхмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвёртой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.

Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Сам же четырёхмерный гиперкуб можно разбить на бесконечное количество кубов, подобно тому, как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.

Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру — развёртку. Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один — грань, ей противоположную. А трёхмерная развёртка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного — конечной «гиперграни».

Гиперкуб в искусстве

Тессеракт настолько интересная фигура, что неоднократно привлекал внимание писателей и кинематографистов.
Роберт Э. Хайнлайн несколько раз упоминал гиперкубы. В «Доме, который построил Тил», (1940) он описал дом, построенный как развёртка тессеракта, а затем вследствие землетрясения «сложившийся» в четвёртом измерении и ставший «реальным» тессерактом. В романе «Дорога славы» Хайнлайна описана гиперразмерная шкатулка, которая была изнутри больше, чем снаружи.

Рассказ Генри Каттнера «Все тенали бороговы» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.

Сюжет фильма «Куб 2: Гиперкуб» сосредотачивается на восьми незнакомцах, пойманных в ловушку в «гиперкубе», или сети связанных кубов.

Математические абстракции вызвали к жизни представление о существовании параллельных миров. Под таковыми понимаются реальности, которые существуют одновременно с нашей, но независимо от неё. Параллельный мир может иметь различные размеры: от небольшой географической области до целой вселенной. В параллельном мире события происходят по-своему, он может отличаться от нашего мира, как в отдельных деталях, так и практически во всём. При этом физические законы параллельного мира не обязательно аналогичны законам нашей Вселенной.

На картине Сальвадора Дали «Распятие на кресте» изображен тессеракт. «Распятие или Гиперкубическое тело», — картина испанского художника Сальвадора Дали, написанная в 1954 году. Изображает распятого Иисуса Христа на развертке тессеракта. Картина хранится в Музее Метрополитен в Нью-Йорке

Всё началось в 1895 году, когда Герберт Уэллс рассказом «Дверь в стене» открыл для фантастики существование параллельных миров. В 1923 году Уэллс вернулся к идее параллельных миров и поместил в один из них утопическую страну, куда отправляются персонажи романа «Люди как боги».

Роман не остался незамеченным. В 1926 году появился рассказ Г. Дента «Император страны „Если»». В рассказе Дента впервые возникла идея о том, что могут существовать страны (миры), история которых могла пойти не так, как история реальных стран в нашем мире. И миры эти не менее реальны, чем наш.

В 1944 году Хорхе Луис Борхес опубликовал в своей книге «Вымышленные истории» рассказ «Сад расходящихся тропок». Здесь идея ветвления времени была, наконец, выражена с предельной ясностью.
Несмотря на появление перечисленных выше произведений, идея многомирия начала серьёзно развиваться в научной фантастике лишь в конце сороковых годов XX века, примерно тогда же, когда аналогичная идея возникла в физике.

Одним из пионеров нового направления в фантастике был Джон Биксби, предположивший в рассказе «Улица одностороннего движения» (1954), что между мирами можно двигаться лишь в одну сторону — отправившись из своего мира в параллельный, вы уже не вернетесь назад, но так и будете переходить из одного мира в следующий. Впрочем, возвращение в свой мир также не исключается — для этого необходимо, чтобы система миров была замкнута.

В романе Клиффорда Саймака «Кольцо вокруг Солнца» (1982) описаны многочисленные планеты Земля, существующие каждая в своём мире, но на одной и той же орбите, и отличаются эти миры и эти планеты друг от друга лишь незначительным (на микросекунду) сдвигом во времени. Многочисленные Земли, которые посещает герой романа, образуют единую систему миров.

В повести братьев Стругацких «Понедельник начинается в субботу» (1962) описаны путешествия персонажей в разные варианты описываемого фантастами будущего — в отличие от уже существовавших в фантастике путешествий в различные варианты прошлого.

Источник

Гиперкуб. Первый шаг в четвертое измерение

Учения о многомерных пространствах начали появляться в середине XIX века в работах Г. Грассмана, А. Кэли, Б. Римана, В. Клиффорда, Л. Шлефли и других математиков. В начале XX века с появлением теории относительности А. Эйнштейна и идей Г. Минковского в физике стали использовать четырехмерную пространственно-временную систему координат.

Потом идею четырехмерного пространства у ученых позаимствовали фантасты. В своих произведениях они поведали миру об удивительных чудесах четвертого измерения. Герои их произведений, используя свойства четырехмерного пространства, могли съесть содержимое яйца, не повредив скорлупы, выпить напиток, не вскрывая пробку бутылки. Похитители извлекали сокровища из сейфа через четвертое измерение. Звенья цепи легко можно рассоединить, а узел на веревке развязать, не прикасаясь к ее концам. Хирурги выполняли операции над внутренними органами, не разрезая ткани тела пациента. Мистики поместили души усопших в четвертое измерение. Для обычного человека идея четырехмерного пространства осталась непонятной и таинственной, а многие вообще считают четырехмерное пространство плодом воображения ученых и фантастов, не имеющего никакого отношения к реальности.

Проблема восприятия

Традиционно считается, что воспринимать и представлять четырехмерные фигуры человек не может, так как он трехмерное существо.

Чтобы составить наглядное представление о четырехмерных фигурах, будем использовать аналогии из пространств низшей размерности для экстраполяции на фигуры высшей размерности, пользоваться методом моделирования, применять методы системного анализа для поиска закономерностей между элементами четырехмерных фигур. Предложенные модели должны адекватно описывать свойства четырехмерных фигур, не противоречить друг другу и давать достаточное представление о четырехмерной фигуре и, в первую очередь, о ее геометрической форме. Так как в литературе нет систематического и наглядного описания четырехмерных фигур, а имеются только их названия с указанием некоторых свойств, мы предлагаем начать изучение четырехмерных фигур с самой простой – четырехмерного куба, который называется гиперкубом.

Определение гиперкуба

Гиперкубом называется правильный политоп, ячейкой которого является куб.

Политоп – это четырехмерная фигура, граница которой состоит из многогранников. Аналогом ячейки политопа является грань многогранника. Гиперкуб является аналогом трехмерного куба.

Мы будем иметь представление о гиперкубе, если познаем его свойства. Субъект воспринимает некоторый объект, представляя его в виде некоторой модели. Воспользуемся данным методом, и представление о гиперкубе изложим в виде различных моделей.

Аналитическая модель

Будем рассматривать одномерное пространство (прямую линию) как упорядоченное множество точек M ( x ), где x – координата произвольной точки прямой. Тогда единичный отрезок задается указанием двух точек: A (0) и B (1).

Плоскость (двумерное пространство) можно рассматривать как упорядоченное множество точек M(x; y). Единичный квадрат будет полностью определен его четырьмя вершинами: A(0; 0), B(1; 0), C(1; 1), D(0; 1). Координаты вершин квадрата получены добавлением к координатам отрезка нуля, а потом единицы.

Трехмерное пространство – упорядоченное множество точек M(x; y; z). Для задания трехмерного куба необходимо восемь точек:

Координаты куба получены из координат квадрата добавлением нуля, а потом единицы.

Четырехмерное пространство есть упорядоченное множество точек M(x; y; z; t). Для задания гиперкуба нужно определить координаты шестнадцати его вершин:

Координаты гиперкуба получены из координат трехмерного куба добавлением четвертой координаты, равной нулю, а потом единице.

Используя формулы аналитической геометрии для четырехмерного евклидового пространства, можно получить свойства гиперкуба.
В качестве примера рассмотрим вычисление длины главной диагонали гиперкуба. Пусть требуется найти расстояние между точками A(0, 0, 0, 0) и R(1, 1, 1, 1). Для этого воспользуемся формулой расстояния в четырехмерном евклидовом пространстве.

В двумерном пространстве (на плоскости) расстояние между точками A(x₁, y₁) и B(x₂, y₂) вычисляется по формуле

Эта формула следует из теоремы Пифагора.

И в одномерном пространстве (на прямой) между точками A(x₁) и B(x₂) можно записать соответствующую формулу расстояния:

Для предложенного примера находим

Таким образом, аналитически гиперкуб существует, и его свойства можно описать не хуже, чем свойства трехмерного куба.

Динамическая модель

Аналитическая модель гиперкуба очень абстрактна, поэтому рассмотрим другую модель – динамическую.

Точка (нульмерная фигура), двигаясь в одном направлении, порождает отрезок (одномерную фигуру). Отрезок, двигаясь в направлении перпендикулярно самому себе, создает квадрат (двумерную фигуру). Квадрат, двигаясь в направлении перпендикулярно плоскости квадрата, создает куб (трехмерную фигуру).

Куб, двигаясь перпендикулярно трехмерному пространству, в котором он находился первоначально, порождает гиперкуб (четырехмерную фигуру).

Граница гиперкуба трехмерна, конечна и замкнута. Она состоит из трехмерного куба в начальном положении, трехмерного куба в конечном положении и шести кубов, образованных при движении квадратов исходного куба в направлении четвертого измерения. Вся граница гиперкуба состоит из 8 трехмерных кубов (ячеек).

При движении в первоначальном положении куб имел 8 вершин и в конечном положении также 8 вершин. Следовательно, гиперкуб имеет в общей сложности 16 вершин.

Из каждой вершины исходят по четыре взаимно перпендикулярных ребра. Всего ребер у гиперкуба – 32. В первоначальном положении у него было 12 ребер, в конечном положении также 12 ребер, и 8 ребер образовали вершины куба при движении в четвертом измерении.

Таким образом, граница гиперкуба состоит из 8 кубов, которые состоят из 24 квадратов. А именно, 6 квадратов в исходном положении, 6 – в конечном, и 12 квадратов, образованных при движении 12 ребер в направлении четвертого измерения.

Геометрическая модель

Динамическая модель гиперкуба может показаться недостаточно наглядной. Поэтому рассмотрим геометрическую модель гиперкуба. Как мы получаем геометрическую модель трехмерного куба? Мы делаем его развертку, а из развертки «склеиваем» модель куба. Развертка трехмерного куба состоит из квадрата, к сторонам которого приложено по квадрату плюс еще один квадрат. 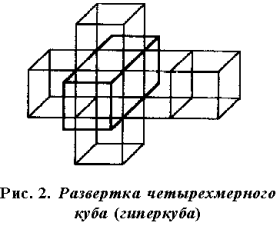Примыкающие квадраты поворачиваем вокруг сторон квадрата, а соседние стороны квадратов соединяем друг с другом. А оставшиеся четыре стороны замыкаем последним квадратом (рис. 1).

Аналогично рассмотрим развертку гиперкуба. Его разверткой будет являться трехмерная фигура, состоящая из исходного трехмерного куба, шести кубов, примыкающих к каждой грани исходного куба и еще одного куба. Всего восемь трехмерных кубов (рис. 2). Чтобы из данной развертки получить четырехмерный куб (гиперкуб), нужно повернуть на 90 градусов каждый из прилегающих кубов. Эти прилегающие кубы будут расположены в другом трехмерном пространстве. Соседние грани (квадраты) кубов соединить друг с другом. Вложить восьмой куб гранями в оставшееся незаполненное пространство. Получим четырехмерную фигуру – гиперкуб, граница которого состоит из восьми трехмерных кубов.

Изображение гиперкуба

Выше было показано, как из трехмерной развертки «склеить» модель гиперкуба. Изображения мы получаем с помощью проекции. Центральная проекция трехмерного куба (его изображение на плоскости) выглядит следующим образом (рис. 3). Внутри квадрата находится другой квадрат. Соответствующие вершины квадрата соединены отрезками. Прилегающие квадраты изображены в виде трапеций, хотя в трехмерном пространстве это квадраты. Внутренний и внешний квадраты разных размеров, но в реальном трехмерном пространстве это равные квадраты.

Аналогично центральная проекция четырехмерного куба на трехмерное пространство будет выглядеть так: внутри одного куба находится другой куб. Соответствующие вершины кубов соединены отрезками. Внутренний и внешний кубы имеют разные размеры в трехмерном пространстве, но в четырехмерном пространстве это равные кубы (рис. 4).

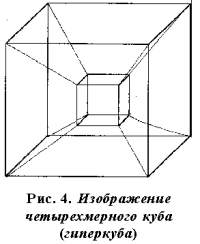
Шесть усеченных пирамид – это изображения равных шести ячеек (кубов) четырехмерного куба.

Эту трехмерную проекцию можно нарисовать на плоскости и убедиться в истинности свойств гиперкуба, полученных с помощью динамической модели.

Гиперкуб имеет 16 вершин, 32 ребра, 24 грани (квадрата), 8 ячеек (кубов). Из каждой вершины исходят по четыре взаимно-перпендикулярных ребра. Границей гиперкуба является трехмерная замкнутая выпуклая фигура, объем которой (боковой объем гиперкуба) равняется восьми единичным трехмерных кубам. Внутри себя эта фигура содержит единичный гиперкуб, гиперобъем которого равняется гиперобъему единичного гиперкуба.

Заключение

В данной работе ставилась цель дать первоначальное знакомство с четырехмерным пространством. Сделано это было на примере самой простой фигуры – гиперкуба.

Мир четырехмерного пространства удивителен! В нем, наряду с похожими фигурами в трехмерном пространстве, существуют и фигуры, аналогов которых нет в трехмерном пространстве.

Многие явления материального мира, макромира и мегамира, несмотря на грандиозные успехи в физике, химии и астрономии, так и остались необъяснимыми.

Нет единой теории, объясняющей все силы природы. Нет удовлетворительной модели Вселенной, объясняющей ее строение и исключающей парадоксы.

Познав свойства четырехмерного пространства и позаимствовав некоторые идеи из четырехмерной геометрии, можно будет не только построить более строгие теории и модели материального мира, но и создать инструменты и системы, функционирующие по законам четырехмерного мира, тогда возможности человека окажутся еще более впечатляющими.

Источник