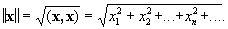что такое гильбертово пространство
Пространство Гильберта
Ги́льбертово простра́нство — особый тип банаховых пространств, обобщение евклидова пространства на бесконечномерный случай. При этом гильбертово пространство не обязательно является бесконечномерным.
Гильбертово пространство есть банахово пространство, норма которого порождена положительно определённым скалярным произведением.
Содержание
Связанные определения
Свойства
Примеры
Для пространств 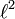
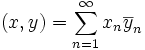
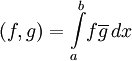
См. также
Литература
Ссылки
Полезное
Смотреть что такое «Пространство Гильберта» в других словарях:
ПРОСТРАНСТВО — фундаментальное (наряду с временем) понятие человеческого мышления, отображающее множественный характер существования мира, его неоднородность. Множество предметов, объектов, данных в человеческом восприятии одновременно, формирует сложный… … Философская энциклопедия
Пространство, время, материя — «ПРОСТРАНСТВО, ВРЕМЯ, МАТЕРИЯ» ставший классическим итоговый труд Г. Вейля по теории относительности (Weyl H. Raum, Zeit, Materie. Verlesungen ueber allgemeine Relativitaetstheorie. Berlin, 1. Aufl. 1918; 5. Aufl. 1923; рус. пер.: Вейль П … Энциклопедия эпистемологии и философии науки
ГИЛЬБЕРТА СХЕМА — конструкция в алгебраич. геометрии, позволяющая снабжать множество замкнутых подмногообразий проективного пространства с заданным Гильберта многочленом структурой алгебраич. многообразия. Более точно, пусть X проективная схема над локально… … Математическая энциклопедия
Бесконечномерное пространство — пространство, содержащее бесчисленное множество линейно независимых элементов. Например, в квантовой механике пространство Гильберта (гильбертово пространство), выражающее бесконечное число квантовых состояний (волновую функцию) системы… … Начала современного естествознания
Оператор Гильберта — Шмидта — это ограниченный оператор A на гильбертовом пространстве H с конечной нормой Гильберта Шмидта, т.е. для которого существует такой ортонормированный базис в H, что Если это верно в каком то ортономированном базисе, то это верно в любом… … Википедия
Пространства Гильберта — Гильбертово пространство особый тип банаховых пространств, обобщение евклидова пространства на бесконечномерный случай. При этом гильбертово пространство не обязательно является бесконечномерным. Гильбертово пространство есть банахово… … Википедия
Гильбертовы пространства
| Определение: |
| Гильбертовым пространством называют Банахово пространство, в котором норма порождена скалярным произведением. |
| Определение: |
| Говорят, что два элемента [math] x, y [/math] гильбертова пространства [math] H [/math] перпендикулярны ( [math] x \perp y [/math] ), если [math] \langle x, y \rangle = 0. [/math] |
Итак, возможность представления [math]x[/math] в форме [math]x=x’+x»[/math] и соотношение [math]\|x-x’\|=\rho(x, H_1)[/math] установлены.
| Теорема (некомпактность шара в бесконечномерном пространстве): |
| Доказательство: |
| [math]\triangleright[/math] |
| Доказательство есть здесь: L_2-теория рядов Фурье. |
| [math]\triangleleft[/math] |
| Теорема (Бессель, неравенство Бесселя): | |||||||||||
Для некоторого набора коэффициентов [math] \beta_k [/math] рассмотрим скалярное произведение: Интересно рассмотреть, когда для всех [math]x[/math] неравенство превращается в равенство.
Можно задаться вопросом: какое топологическое свойство характеризует существование ортонормированного базиса? [math]\exists A = \< a_1 \dots a_n \dots \>, \mathrm Гильбертово пространствоПолезноеСмотреть что такое «Гильбертово пространство» в других словарях:ГИЛЬБЕРТОВО ПРОСТРАНСТВО — математическое понятие, обобщающее понятие евклидова пространства на бесконечномерный случай. Возникло на рубеже 19 и 20 вв. в работах Д. Гильберта; находит широкое приложение в различных разделах математики и теоретической физики … Большой Энциклопедический словарь Гильбертово пространство — Сюда перенаправляется запрос «теорема Рисса Фишера». На эту тему нужна отдельная статья. Гильбертово пространство обобщение евклидова пространства, допускающее бесконечную размерность. Названо в честь Давида Гильберта. Со … Википедия гильбертово пространство — математическое понятие, обобщающее понятие евклидова пространства на бесконечномерный случай. Возникло на рубеже XIX и XX вв. в работах Д. Гильберта; находит широкие приложения в различных разделах математики и теоретической физики. * * *… … Энциклопедический словарь гильбертово пространство — Hilberto erdvė statusas T sritis fizika atitikmenys: angl. Hilbert space vok. Hilbert Raum, m rus. гильбертово пространство, n pranc. espace de Hilbert, m; espace hilbertien, m … Fizikos terminų žodynas Гильбертово пространство — обобщение евклидова пространства на бесконечномерный случай (пространство с бесконечным количеством размерностей). В таком пространстве сумма квадратов всех элементов пространства сходится, т. е. конечна, как конечна сумма квадратов сторон… … Начала современного естествознания ГИЛЬБЕРТОВО ПРОСТРАНСТВО — матем. понятие, обобщающее понятие евклидова пространства па бесконечномерный случай. Возникло на рубеже 19 и 20 вв. в работах Д. Гильберта; находит широкие приложения в разл. разделах математики и теоретич. физики … Естествознание. Энциклопедический словарь гильбертово пространство — г ильбертово простр анство, г ильбертова простр анства … Русский орфографический словарь ГИЛЬБЕРТОВО ПРОСТРАНСТВО С ИНДЕФИНИТНОЙ МЕТРИКОЙ — гильбертово пространство Е над полем комплексных чисел, снабженное непрерывной билинейной (точнее полуторалинейной) формой G, к рая, вообще говоря, не является положительно определенной. Форму Gчасто наз. G метрикой. Наиболее важным частным… … Математическая энциклопедия Часть IIНовая физика, необходимая для понимания разума. В поисках невычислительной физики разума5. Структура квантового мира5.12. Гильбертово пространствоЧтобы более внятно (и более точно) рассказать о том, как работает процедура R в стандартных квантовомеханических описаниях, необходимо перейти на несколько (совсем немного) более высокий уровень математической абстракции. Семейство всех возможных состояний квантовой системы образует так называемое гильбертово пространство. Нужды объяснять значение этого термина во всех математических тонкостях у нас в данный момент нет, однако некоторое представление о нем все же получить стоит — это поможет нам прояснить существующую картину квантового мира. Первая и наиболее важная особенность, на которую следует обратить внимание: гильбертово пространство является комплексным векторным пространством. Это, в сущности, означает, что здесь мы вправе выполнять действия с комплексно-взвешенными комбинациями, посредством которых описываются квантовые состояния. Для обозначения элементов гильбертова пространства я продолжу использовать диракову скобку «кет», т.е. если состояния |ψ〉 и |φ〉 являются элементами гильбертова пространства, то таким же его элементом является и состояние w|ψ〉 + z|φ〉, где w и z — любая пара комплексных чисел. Допускается даже комбинация w = z = 0, она дает элемент 0 гильбертова пространства — единственный элемент, не соответствующий никакому возможному физическому состоянию. Как и в любом другом векторном пространстве здесь действуют самые обыкновенные алгебраические правила: а это более или менее означает, что мы можем использовать алгебраическую систему обозначений привычным нам образом. Иногда гильбертово пространство имеет конечную размерность — как, например, при описании спиновых состояний частицы. В случае спина 1/2 гильбертово пространство двумерно, а его элементы представляют собой комплексные линейные комбинации двух состояний, |↑〉 и |↓〉. Для спина 1/2 n гильбертово пространство (n + 1)-мерно. Однако размерность гильбертова пространства может быть и бесконечной — такое пространство необходимо, например, для описания состояний положения частицы. В этом случае каждое альтернативное положение, которое может занимать частица, рассматривается как отдельное измерение гильбертова пространства. Общее же состояние, определяющее квантовое местоположение частицы, записывается как комплексная суперпозиция всех этих различных отдельных положений (волновая функция для данной конкретной частицы). Надо сказать, что с рассмотрением такого бесконечномерного гильбертова пространства связаны определенные математические осложнения, которые лишь запутают нас без всякой на то необходимости, поэтому ниже я сосредоточусь (в основном) на конечномерном случае. Попытавшись представить гильбертово пространство визуально, мы сталкиваемся с двумя трудностями. Во-первых, размерность такого пространства, как правило, слишком велика для того, чтобы наше воображение сколько-нибудь адекватно справилось с задачей. Во-вторых, пространство это является не вещественным, но комплексным. Впрочем, часто бывает полезно не задумываться о подобных трудностях с самого начала — это помогает выработать некоторое интуитивное понимание математических аспектов концепции. Поэтому давайте на некоторое время сделаем вид, будто для представления гильбертова пространства вполне достаточно той привычной двух- или трехмерной картины, которая у нас уже есть. На рис. 5.22 проиллюстрирована геометрически операция линейной суперпозиции на примере обычного трехмерного пространства. Рис. 5.22. Если вообразить, что гильбертово пространство тождественно трехмерному евклидову пространству, то сумму векторов |ψ〉 и |φ〉 можно найти с помощью обычного правила параллелограмма (в плоскости (0, |ψ〉, |φ〉). Вспомним, что вектор квантового состояния |ψ〉 соответствует тому же физическому состоянию, что и любой кратный ему вектор u|ψ〉, где u — ненулевое комплексное число. В нашей геометрической интерпретации это означает, что физическое состояние представляется не одинокой точкой в гильбертовом пространстве, но прямой, соединяющей гильбертову точку |ψ〉 с началом координат 0 (такую прямую называют лучом). Пример луча изображен на рис. 5.23; следует, впрочем, учитывать, что ввиду комплексного характера гильбертова пространства луч этот только выглядит как обычная одномерная прямая, на деле же за ним скрывается целая комплексная плоскость. Рис. 5.23. Луч в гильбертовом пространстве есть множество всех комплексных кратных вектора состояния |ψ〉. Мы представляем этот луч в виде прямой, проходящей через начало гильбертовых координат, однако не следует забывать о том, что за этой прямой на деле скрывается комплексная плоскость. До сих пор мы рассматривали гильбертово пространство, имея в виду лишь то, что структурно оно представляет собой комплексное векторное пространство. Однако, помимо комплексно-векторной структуры, у гильбертова пространства имеется еще одно, не менее важное, свойство, крайне полезное для описания процедуры редукции R. Речь идет об эрмитовом скалярном произведении (или внутреннем произведении), каковая операция позволяет из любой пары гильбертовых векторов получить одно-единственное комплексное число. Она же дает нам возможность ввести два весьма важных понятия. Первое — квадрат длины гильбертова вектора как скалярное произведение вектора на самого себя. Например, нормированное состояние (необходимое, как мы отмечали выше — см. §5.8, — для строгой применимости правила квадратов модулей) задается гильбертовым вектором, квадрат длины которого равен единице. Вторым важным понятием, сопутствующим скалярному произведению, является понятие ортогональности гильбертовых векторов — векторы ортогональны, когда их скалярное произведение равно нулю. Ортогональными считаются векторы, направленные, в том или ином смысле, «под прямым углом» друг к другу. Применительно к состояниям, ортогональными обычно называют состояния, независимые одно от другого. Важность этого понятия для квантовой физики заключается в том, что различные альтернативные результаты любого измерения всегда ортогональны друг другу. В качестве примера ортогональных состояний можно привести состояния |↑〉 и |↓〉, с которыми мы встречались при рассмотрении частицы со спином 1/2. (Отметим, что ортогональность в гильбертовом пространстве, как правило, не соответствует перпендикулярности в пространстве обычном; в случае спина 1/2 ортогональные состояния |↑〉 и |↓〉 представляют физические конфигурации, ориентированные, скорее, в противоположных направлениях, нежели под прямым углом.) Следующий пример — состояния |↑↑…↑〉, |↓↑…↑〉, …, |↓↓…↓〉 спина 1/2 n; каждое такое состояние ортогонально всем остальным. Ортогональными являются и все различные возможные положения, в которых может находиться квантовая частица. Более того, ортогональны как состояния |B〉 и i|C〉 (см. §5.7 — прошедшая и отраженная части состояния фотона, получаемые в результате падения фотона на полупрозрачное зеркало), так и состояния i|D〉 и —|E〉, в которые эволюционируют первые два после отражения от двух непрозрачных зеркал. Последний факт иллюстрирует одно важное свойство шрёдингеровой эволюции U. Любые два изначально ортогональных состояния ортогональными и остаются, если каждое эволюционирует в соответствии с U в течение одного и того же временного периода. Таким образом, свойство ортогональности при эволюции U сохраняется. Кроме того, эволюция U сохраняет и значение скалярного произведения состояний. Собственно, именно в этом и заключается формальный смысл понятия унитарная эволюция. Как мы только что отметили, ортогональность математически выражается как обращение в нуль скалярного произведения состояний. Это скалярное произведение, в общем случае, представляет собой комплексное число, поставленное в соответствие какой-либо паре элементов гильбертова пространства. Если обозначить эти элементы (или состояния) через |ψ〉 и |φ〉, то упомянутое комплексное число записывается так: 〈ψ|φ〉. При этом выполняется ряд простых алгебраических тождеств, которые мы можем записать в следующем (несколько, правда, неуклюжем) виде: Кроме того, можно показать, что 〈ψ|ψ〉 = 0 при |ψ〉 = 0. Мне не хочется надоедать читателю прочими математическими подробностями (если же таковые подробности кого-то заинтересуют, то ознакомиться с ними можно, открыв любой стандартный текст по квантовой теории; см., например, [94]). Существенными для наших дальнейших нужд свойствами скалярного произведения являются лишь следующие два (уже, впрочем, упоминавшиеся выше): векторы |ψ〉 и |φ〉 ортогональны тогда и только тогда, когда 〈ψ|φ〉 = 0, произведение 〈ψ|ψ〉 есть квадрат длины вектора |ψ〉. Отметим, что отношение ортогональности является симметричным (поскольку 〈ψ¯|¯φ〉 = 〈φ|ψ〉). Более того, произведение 〈ψ|ψ〉 всегда представляет собой неотрицательное вещественное число, из какового числа легко извлекается неотрицательный квадратный корень, который мы можем называть длиной (или величиной) вектора |ψ〉. Читайте еще:Это случилось, когда я пошел в начальную школу. Родители определили меня в группу, где были эмоционально не стабильные дети, а так же дети с проблемами развития умственно отсталые. Должно быть они чувствовали, что со мной что-то не так. Но это оказалось простой потерей времени. К тому времени я. Это замечательное, продуктивное решение, которое, если оно случается, цементирует брак необычайным образом. Потому что здесь в основу кладется сотрудничество, есть общая цель, общие задачи. А главное – люди не чувствуют себя одинокими, поскольку рядом у них товарищ, плечо, так сказать, человек. Вот только тогда все слова формулы, которые произносит про себя занимающийся, равносильны приказам гипнотизера при воздействии его на гипнотизируемого. Единственное отличие в том, что при занятиях AT, человек находящийся в «трансе», сам себе дает установки и соответствующие настрои, сохраняя при. Поэтому-то людям и стало «тесно» в смысле сосуществования с себе подобными: людоедство стало неотъемлемым атрибутом — в начале — экологии популяции, а затем «успешно» перекочевало и в быт сообществ. Именно этим и объясняется дивергенция человечества. Ничем иным не объясним. Вера основана на абсолютной уверенности. Вера – это знание. Вы ни капли не сомневаетесь в том, что вы знаете, и можете рассчитывать на это. Я знаю, что завтра взойдет солнце. Я верю в это. Я знаю, что Бог есть и что Он хочет всего наилучшего для меня: здоровья, процветания, успеха и счастья. Я в. Стоит отметить, что философское измерение психоанализа, включающее в себя наиболее общие положения о существовании психической реальности как реальности особого рода, примате бессознательной системы в психике человека и наличии причинной обусловленности психических процессов и явлений, выступает. В каждом ребенке просыпается художник. Вообразим ситуацию, в которой друг пришел к художнику. Видя, что художник упорно трудится, желая облегчить ему жизнь, друг приносит ему готовую картину. В лучшем случае художник выразит недоумение, а в худшем – обидится. Эта ситуация является аналогом. Мне удается веpнуться к вчеpашнему сну лишь в кабинете. До пpихода пеpвого пациента остается десять минут. Свистит чайник, заваpиваю чай. Сижу в своем кpесле-качалке, пpистально глядя на стоящее напpотив кpесло для пациентов. Ничто не радует, все валится из рук, не хочется никого видеть, неприятно думать о будущем – кому из нас не знакома такая картина. Одни называют это приступом меланхолии, другие – депрессией. Дети стали еще одним убедительным доказательством силы любви и правильности избранного пути. И дело тут вовсе не в безупречном образовании, которое родители обеспечили сыновьям. Получив исключительные знания языков все в той же гимназии Карла Мая, Юрий закончил индо-иранское отделение Школы. Гениям во все времена приписывали огромный спектр отличительных особенностей: от божественного вдохновения и сверхчеловеческой «искры» до физических дефектов и безумия. Все эти разнообразные теории могут быть разделены по принципу лежащего в их основе предположения. Их четыре, и соответственно. Проблемы требуют внимания. Кризисы нужно преодолевать. Под усовершенствованием часто понимают всего лишь мероприятия, направленные на удешевление производства. К сожалению, нет простого способа для того, чтобы побудить людей к поиску новых возможностей. Для этого нужен дух предпринимательства. ГИЛЬБЕРТОВО ПРОСТРАНСТВОвекторное пространство Н над полем комплексных (или действительных) чисел вместе с комплексной (действительной) функцией ( х, у), определенной на и обладающей следующими свойствами. элемент хназ. пределом последовательности ; Иногда в определение Г. п. не включается условие бесконечномерности, т. е. предгильбертовым пространством наз. векторное пространство над полем комплексных (или действительных) чисел со скалярным произведением, а Г. п. наз. полное предгильбертово пространство. Примеры Г. п. 1) Комплексное пространство (или l2). Элементами этого Г. п. являются бесконечные последовательности комплексных чисел со сходящейся суммой квадратов модулей: скалярное произведение определяется равенством сходится. Скалярное произведение определяется равенством Всякое Г. п. изоморфно пространству для нек-рого соответствующим образом подобранного Т. В этом Г. п. скалярное произведение определяется равенством 4) Соболева пространство , обозначаемое также (см. Вложения теоремы). где dx— мера Лебега на (вместо меры Лебега можно взять любую другую положительную счетно аддитивную меру). Если на этом множестве функций определить скалярное произведение 6) Множество непрерывных Бора почти периодических функций на прямой образует предгильбертово пространство, если скалярное произведение определяется равенством Пространства l 2 и L 2 были введены и изучены Д. Гильбертом [1] в основополагающих работах по теории интегральных уравнений и бесконечных квадратичных форм. Определение Г. п. было дано Дж. Нейманом [3], Ф. Риссом [4] п М. Стоуном [13], к-рые положили также начало его систематич. изучению. Множество наз. ортонормиро ванным множеством, или ортонормпрованной системой, если любые различные два вектора из Аортогональны и если норма каждого вектора равна единице. (теорема Пифагора в Г. п.). Некоторые из геометрич. понятий требуют использования терминологии линейных операторов в Г. п.; к ним относится, в частности, понятие раствора линейных многообразий. Раствором многообразий и в Г. п. Н наз. норма разности операторов, проектирующих Нна замыкание этих линейных многообразий. Простейшие свойства раствора: Во многих задачах, относящихся к Г. п., участвуют лишь конечные наборы векторов Г. п., т. е. элементы конечных линейных многообразий Г. п. Поэтому понятия и методы линейной алгебры играют в теории Г. п. большую роль. Векторы в Г. п. наз. линейно независимыми, если равенство В множестве Г. п. определены операции прямой суммы и тензорного произведения Г. п. Прямой суммой Г. п. где каждое обладает соответствующим скалярным произведением, наз. Г. п. При элементы из и в прямой сумме При этом в Нлинейные операции определяются равенством При таком способе введения линейных операций и скалярного произведения прямая сумма Г. п. образуют важный класс банаховых пространств:любое Г. и. Hесть банахово пространство относительно нормы причем для любых двух векторов имеет место равенство параллелограмма: Равенство параллелограмма выделяет класс Г. и. среди банаховых пространств, т. е. если в действитель-яия нормированном пространстве Бдля любой пары элементов л-, . имеет место равенство параллелограмма, то функция Как и в теории общих банаховых пространств, в теории Г. п. важную роль играет понятие сепарабельности. Г. п. сепарабельно тогда и только тогда, когда оно имеет счетную размерность. Г. п. и сепара-бельны. Г. п. сепарабельно тогда и только тогда, когда Тне более чем счетно; Г. п. сепарабельно, если мера имеет счетный базис. Г. п. не сепарабельно. Основным содержанием теории Г. н. является теория линейных операторов в Г. п. Само понятие Г. п. сформировалось в работах Д. Гильберта [2] и Э. Шмидта [14] по теории интегральных уравнений, а абстрактное определение Г. п. было дано в работах Дж. Неймана [3], Ф. Рисса [4] и М. Стоуна [13] по теории эрмитовых операторов. Теория операторов в Г. п. представляет особый важный раздел общей теории операторов но двум причинам. Во-вторых, интенсивно развивающаяся теория несамосопряженных операторов в Г. п. (в частности, циклических, нильпотентных, одноклеточных, сжимающих, спектральных и скалярных операторов) является важной моделью теории линейных операторов в более общих пространствах. Важный класс линейных операторов в Г. п. образуют всюду определенные непрерывные операторы, наз. также ограниченными операторами в Г. п. Если ввести в множестве всех ограниченных линейных операторов в H операции сложения, умножения на число и умножения операторов, а также норму оператора, по обычным правилам (см. Линейные операторы).и определить инволюцию в как переход к сопряженному оператору, то становится банаховой алгеброй с инволюцией. Важнейшими классами ограниченных операторов в Г. п. являются самосопряженные операторы, унитарные операторы и нормальные операторы, так как они обладают специальными свойствами по отношению к скалярному произведению. Эти классы операторов хорошо изучены; основным инструментом в их изучении являются простейшие из ограниченных самосопряженных операторов, а именно: операторы ортогонального проектирования, или ортогональные проекторы, часто называемые просто проекторами. Способ, позволяющий строить любые ограниченные самосопряженные, унитарные и нормальные операторы в комплексном Г. п. с помощью проекторов, дается спектральным разложением соответствующих операторов, особенно простым в случае сепарабельного Г. п. Более сложным разделом теории линейных операторов в Г. п. является теория неограниченных операторов. Важнейшими неограниченными операторами в Г. н. являются замкнутые линейные операторы с плотной областью определения; в частности, неограниченные самосопряженные и нормальные операторы. Между самосопряженными и унитарными операторами в Г. п. существует взаимно однозначное соответствие, определяемое Кэли преобразованием. Большое значение имеет (в частности, в теории линейных дифференциальных операторов) класс симметричных операторов в Г. п. и теория самосопряженных расширений симметричных операторов. Неограниченные самосопряженные и нормальные операторы в комплексном Г. и. H также допускают спектральное разложение. Спектральное разложение является большим достижением теории самосопряженных и нормальных операторов в Г. п. Оно соответствует классич. теории приведения эрмитовых и нормальных комплексных матриц в n-мерном унитарном пространстве. Именно спектральное разложение и связанное с ним операторное исчисление для самосопряженных и нормальных операторов обеспечивают теории операторов в Г. п. широкую область применения во многих разделах математики. Для ограниченных самосопряженных операторов в спектральное разложение было найдено Д. Гильбертом [1], к-рый также ввел важное понятие разложения единицы для самосопряженного оператора. В современный период известно несколько подходов к спектральной теории самосопряженных и нормальных операторов. Один из наиболее глубоких дает теория банаховых алгебр. Спектральное разложение для неограниченного самосопряженного оператора было найдено Дж. Нейманом [3]. Его работе предшествовали важные исследования Т. Карлемана [8], к-рый получил спектральное разложение для случая симметрического интегрального оператора, а также впервые обнаружил, что между симметрическими ограниченными и неограниченными операторами полной аналогии нет. На важность понятия самосопряженного оператора впервые обратил внимание Э. Шмидт (см. [3], с. 62). Следует отметить, что как для исследований Д. Гильберта, так и для более поздних исследований большое значение имели работы П. Л. Чебышева, А. А. Маркова, Т. И. Стилтьеса по классической моментов проблеме, Якоби матрицам и непрерывным дробям (см. [9]). Лит.:[1] Нilbеrt D., Grundziige einer allgemeincn Theorie der linearen Integralgleichungen, Lpz.- В., 1912; N. Y., 1953; [2] Вesiсоvitсh A. S., Almost periodic functions, Camb., 1932; [3] vоn Neumann J., «Math. Ann.», 1929, Bd 102, S. 49-131; [4] Riesz P., «Acta Sci. Math. Szeged», 1930, v. 5, № 1, p. 23-54; [5] Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964; [6] Бурбаки Н., Топологические векторные пространства, пер. с франц., М., 1959; [7] Ахиезер Н. И., Глазман И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966; [8] Саrlеmаn Т., Sur les equations integrates singulieres a noyau reel et symetrique, Uppsala, 1923; [9] Axиезер Н. И., Классическая проблема моментов и некоторые вопросы анализа, связанные с нею, М., 1961; [10] Данфорд Н., Шварц Д ж., Линейные операторы, пер. с англ., М., 1962; [11] Рисе Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; [12] Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [13] Stone M., Linear transformation in Hilbert space and their applications to analisis, N. Y., 1932; [14] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972. |