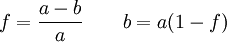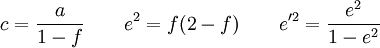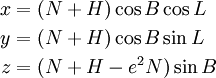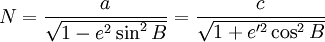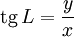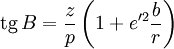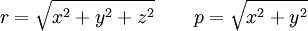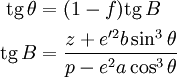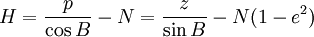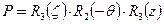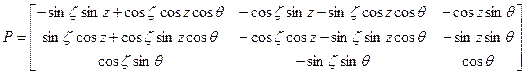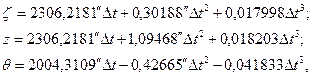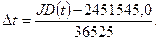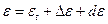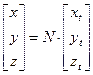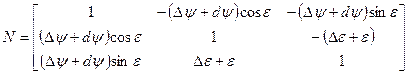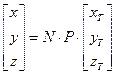что такое геоцентрическая система координат

Геоцентрические системы координат

Системы координат

Необходимость в использовании различных координатных систем в спутниковых технологиях обусловлена тем, что для вычисления орбит спутников и прогнозирования их движения применяются одни системы координат, а для определения пространственного положения точек требуются другие системы координат.

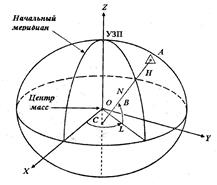
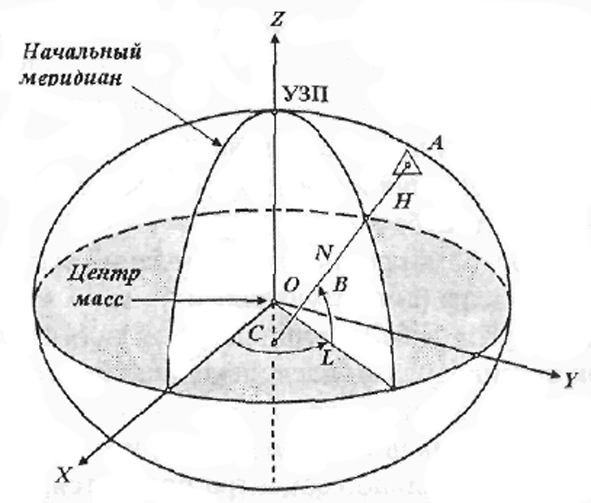
Системы, начало которых совпадает с центром масс Земли, называют геоцентрическими [34]. Земными (рис. 1) – называют системы, вращающиеся вместе с Землей и у которых:

— ось z проходит через условный земной полюс (УЗП);

— ось x проходит через точку G пересечения плоскостей экватора и начального меридиана;

— ось y дополняет систему до правой.

Рисунок 1. Геоцентрическая земная система координат

На рисунке 1 обозначено: О – начало координат, В – геодезическая широта, L – геодезическая долгота, Н – геодезическая высота, А – точка находящаяся на физической поверхности Земли, а – проекция точки А на поверхность эллипсоида, N = ac – радиус кривизны эллипсоида в плоскости первого вертикала.

В геодезии используют общеземную систему координат, которая должна отвечать следующим условиям:

— начало координат совмещается с центром масс Земли;

— масса эллипсоида должна равняться массе Земли;

— эллипсоид должен наиболее лучше описывать физическую поверхность Земли.

Для определения геодезических координат требуется знать параметры земного эллипсоида. Параметры некоторых общеземных эллипсоидов приведены в таблице 1.

Параметры для эллипсоидов WGS-84, ПЗ-90 и Красовского

Для решения геодезических задач требуется так же знать и гравитационное поле Земли. А для того, чтобы осуществить пересчет из одной системы в другую, необходимо знать параметры преобразований.

Все геоцентрические системы связаны с определенными эллипсоидами, название которых обычно совпадают с названием самой системы. В этом случае возможно использование не только декартовых, но и эллипсоидальных координат: геодезическая широта B, геодезическая долгота L и геодезическая высота H (см. рисунок 1).

Источник

GIS-LAB

Географические информационные системы и дистанционное зондирование

Геодезические системы пространственных координат

Рассматриваются преобразования между пространственными координатными системами. Приводится пример программной реализации на языке Питон.

Содержание

[править] Земной эллипсоид

Земным эллипсоидом называется эллипсоид вращения, поверхность которого по форме и размерам довольно близка к поверхности геоида.

Поверхность эллипсоида образуется вращением эллипса вокруг его малой оси, которая также является осью вращения эллипсоида.

Эллипс обычно определяется размером его большой полуоси a и сжатием f. Реже вместо сжатия задаётся размер малой полуоси b:

В теории и практике вычислений широко используются такие параметры, как полярный радиус кривизны поверхности c, первый эксцентриситет e и второй эксцентриситет e′:

Пример функции Питона, вычисляющей по a и f параметры b, c, e и e′:

[править] Системы координат

Рассмотрим следующие системы координат.

Помимо широкого использования в геодезических целях, каждая из представленных координатных систем находит важное применение в прикладных областях.

Геодезические координаты со времён седой древности используются в навигации и картографии. В картографии они являются основой построения проекций.

Геоцентрическая система координат необходима для вычисления спутниковых орбит и решения других орбитальных задач.

Проекции, используемые картографами различных стран, основаны на различных геодезических датумах, т.е. созданы на различных эллипсоидах с разными размерами, положением центров и ориентацией осей в пространстве. Самый простой и точный способ пересчёта координат, заданных в разных датумах, зиждется на преобразованиях между геодезическими и геоцентрическими системами. В общем случае схема пересчёта координат между двумя проекциями выполняется в пять этапов:

Топоцентрическая система координат — естественная система для работы различных наземных объектов: ракетных стартовых комплексов, станций слежения за спутниками, станций ПВО и других измерительных комплексов. Естественно, собираемая информация в каждом случае преобразуется в общую систему координат, связанную с Землёй — геодезическую систему координат.

[править] Преобразования координат

[править] Переход от геодезических координат к геоцентрическим

Это преобразование выполняется по следующим формулам:

Здесь N — так называемый радиус кривизны первого вертикала:

Реализация на Питоне:

[править] Переход от геоцентрических координат к геодезическим

Проще всего вычисляется долгота:

Сложнее с определением широты и высоты. Существует множество способов решения этой задачи. Воспользуемся итеративным методом Боуринга.

В начале находится предварительная оценка широты B:

Здесь r — геоцентрический радиус-вектор, p — расстояние от оси вращения эллипсоида:

Затем вычисляется параметр θ (приведённая широта) и получается уточнённое значение широты:

Действия по последним двум формулам предполагается повторять до сходимости к требуемой точности. Как правило, бывает достаточно одной итерации. В примере реализации метода Боуринга, приведённом ниже, запрограммировано две итерации.

В конце определяется высота:

[править] Переход от геоцентрических координат к топоцентрическим

Постановка задачи: начало топоцентрической системы координат задано точкой Q₀ (B₀, L₀, H₀); по геоцентрическим координатам точки Q (x, y, z) вычислить её топоцентрические координаты.

Конформное преобразование между двумя декартовыми прямоугольными системами координат всегда может быть представлено последовательностью сдвигов и вращений координатной системы. Данное преобразование можно реализовать по следующему алгоритму:

Функция toTopo() содержит обращения к функции вращения rotate():

[править] Переход от топоцентрических координат к геоцентрическим

Постановка задачи: начало топоцентрической системы координат задано точкой Q₀ (B₀, L₀, H₀); по топоцентрическим координатам точки Q (x, y, z) вычислить её геоцентрические координаты.

Алгоритм решения получается обращением алгоритма обратной задачи:

[править] Переход от геодезических координат к топоцентрическим. Обратная пространственная задача

Постановка задачи: начало топоцентрической системы координат задано точкой Q₀ (B₀, L₀, H₀); по геодезическим координатам точки Q (B, L, H) вычислить её топоцентрические координаты x, y, z.

Задача решается последовательным применением готовых алгоритмов:

Рассмотренная задача является разновидностью обратной геодезической задачи в пространстве. Вместо декартовых прямоугольных топоцентрических координат может требоваться вычисление каких-то других связанных с ними величин, например, полярных координат «дальность-азимут-зенитное расстояние», варианты могут быть разные. Однако в большинстве случаев сначала находятся топоцентрические x, y, z, по которым и выводятся искомые значения.

[править] Переход от топоцентрических координат к геодезическим. Прямая пространственная задача

Постановка задачи: начало топоцентрической системы координат задано точкой Q₀ (B₀, L₀, H₀); по топоцентрическим координатам точки Q (x, y, z) вычислить её геодезические координаты B, L, H.

Задача решается через вычисление геоцентрических координат:

Эта задача является разновидностью прямой геодезической задачи в пространстве. Вместо декартовых прямоугольных топоцентрических координат могут задаваться какие-то другие связанные с ними величины, например, полярные координаты «дальность-азимут-зенитное расстояние», варианты могут быть разные. Однако в большинстве случаев сначала находятся топоцентрические x, y, z, по которым и решается задача.

[править] Пример программной реализации

Коды вышеприведённых функций находятся в архиве Spheroid.zip в файле spheroid.py. Напишем программы, которые используют их для преобразования координат.

[править] Пересчёт топоцентрических координат в геодезические

В этом примере программы явно задаются параметры эллипсоида a, f и геодезические координаты начала топоцентрической системы B₀, L₀, H₀. Координаты точек x, y, z читаются из файла данных и пересчитанные значения B, L, H выводятся в консоль.

Этот скрипт находится в архиве Spheroid.zip в файле forwrd3d.py.

Файл данных должен содержать в каждой строке координаты одной точки x, y, z, разделённые пробелом. Создадим файл данных fwd3d.dat:

Выполним скрипт в командной строке:

Координаты на выходе:

Запишем полученные координаты в файл результатов inv3d.dat:

[править] Пересчёт геодезических координат в топоцентрические

В этом примере программы явно задаются параметры эллипсоида a, f и геодезические координаты начала топоцентрической системы B₀, L₀, H₀. Координаты точек B, L, H читаются из файла данных и пересчитанные значения x, y, z выводятся в консоль.

Этот скрипт находится в архиве Spheroid.zip в файле invers3d.py.

Файл данных должен содержать в каждой строке координаты одной точки B, L, H, разделённые пробелом. Используем в качестве файла данных созданный выше inv3d.dat:

Выполним скрипт в командной строке:

Координаты на выходе:

[править] Ссылки

Последнее обновление: 2017-03-07 09:34

Дата создания: 23.03.2014
Автор(ы): ErnieBoyd

Источник

Что такое геоцентрическая система координат

Система общеземных геоцентрических прямоугольных координат, фиксированная по отношению к Земле, определяется следующим образом:

Система показана на рис. 1.5, ее оси обозначены как X, Y, Z.

Земные геоцентрические системы реализуются в виде геодезических сетей, построенных методами космической геодезии (или с обязательным привлечением методов космической геодезии). Пункты таких сетей распределены по всему земному шару или по значительной его части. Чем более точны положения этих точек, тем меньше остаточные ошибки и более точна реализация координатной системы.

Эллипсоид

Эллипсоидом называется геометрическое тело, образованное вращением эллипса вокруг его малой оси.

Другие параметры, определяющие размеры и форму эллипсоида, например полярный радиус b и эксцентриситет e, можно вычислить по этим двум параметрам:

Из других параметров нужно указать параметры, представляющие гравитационное поле Земли, параметры связи с другими системами координат. Поэтому, когда говорят о современной геоцентрической земной системе координат (или системе отсчета), подразумевают систему геодезических параметров Земли. В табл. 1.1 приводятся некоторые геодезические параметры для пяти систем.

Источник

Системы координат в геодезии — какие бывают и как используются?

В данной статье мы разбираем основные вопросы по геодезии. Что такое системы координат, какие виды СК выделяют, какие из них используются на практике и для чего. А также, отвечаем на вопрос, почему мы предоставляем поправки в международной системе координат.

Содержание статьи:

Надеемся, этот материал поможет получить ответы на интересующие вопросы.

Что такое система координат?

Система координат (СК) — это набор математических правил, описывающих, как координаты должны быть соотнесены с точками пространства.

Иными словами, это совокупность условий, определяющих положение и перемещение точки или объекта на прямой, на плоскости, в пространстве с помощью чисел или других символов.

Совокупность чисел, определяющих положение точки, называется координатами этой точки.

Какие бывают системы координат?

Существуют разные геодезические системы координат, они используются в зависимости от масштаба, в котором необходимо произвести расчет расположения объекта на Земле.

В рамках данной статьи, разберемся, какие именно бывают системы координат и как используются на практике в геодезии.

Полярная система координат (полярные координаты)

Полярная система координат — это система координат, положение точки в которой задается расстоянием и направлением от ее начала.

Двумерная полярная система координат может быть задана на плоскости, поверхности сферы или эллипсоида.

Плоская прямоугольная (прямолинейная система координат)

Плоская прямоугольная (прямолинейная) система координат — это система координат, определяющая положение точек по отношению к взаимно перпендикулярным осям, исходящим из ее начала.

Координаты точки в данной системе координат представлены в виде плоских прямоугольных координат x и y. В геодезии — это координаты на плоскости, на которой отображена поверхность земного эллипсоида в заданной картографической проекции.

Прямоугольная пространственная система координат

Прямоугольная пространственная система координат — это система трехмерных линейных прямоугольных координат по координатным осям Х, У, Z координат, у которой оси Х и У лежат в экваториальной плоскости, ось Х направлена к начальному меридиану, ось Z направлена на север, орты образуют правую тройку векторов, а начало координат совпадает с центром земного эллипсоида.

Координаты точки в пространственной системе координат представлены в виде геодезических (эллипсоидальных) координатах или в прямоугольных пространственных координатах.

Земные и референцные системы координат

Помимо вышеупомянутых, различают земные (общеземные) и референцные системы координат. Разбираемся, чем они отличаются.

Что такое земная система координат в геодезии?

Земная система координат — это пространственная система координат, предназначенная для количественного описания положения и движения объектов, находящихся на поверхности Земли и в околоземном пространстве.

Что такое референцная система координат в геодезии?

Референцная система координат — это система координат, созданная с целью обеспечения геодезических и картографических работ на конкретной территории. К ним можно отнести местные и условные системы координат.

Что такое геодезическая система координат?

Геодезическая система координат — это система координат, которая используется для определения точного местоположения объекта на земном шаре.

За земной шар, для удобства проведения математических расчетов в инженерной геодезии, принимают шар с R=6371.11 км. Объем земного шара при этом равен объему земного эллипсоида.

Что такое геодезические координаты?

Геодезические координаты — это величины, два из которых (геодезическая широта B и геодезическая долгота L) характеризуют направление нормали к поверхности отсчетного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третий (геодезическая высота H) представляет собой высоту точки над поверхностью отсчетного эллипсоида.

В земных системах координат центр координат совпадает с центром масс Земли, поэтому прямоугольные пространственные координаты называют геоцентрическими координатами.

Системы координат также подразделяют на государственные, местные, локальные и международные.

СК, используемые на практике

Практическими реализациями пространственной геоцентрической земной системы координат являются системы координат WGS-84, ПЗ-90.11 и ГСК-2011.

Система координат WGS-84

WGS-84 (World Geodetic System (Всемирная геодезическая система координат)) – это система геодезических параметров Земли 1984 года, используемая в GPS, в число которых входит система геоцентрических координат).

Система координат ПЗ-90.11

ПЗ-90.11 (общеземная геоцентрическая система координат «Параметры Земли 1990 года») — это государственная система координат, используемая в ГЛОНАСС.

ПЗ-90.11 была установлена постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования в целях геодезического обеспечения орбитальных полетов, решения навигационных задач и выполнения геодезических и картографических работ в интересах обороны Российской Федерации.

Система координат ГСК-2011

ГСК-2011 (геодезическая система координат 2011 года) – это государственная система координат, установленная постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования при осуществлении геодезических и картографических работ на территории Российской Федерации.

Система координат МСК

МСК – это местная система координат субъекта Российской Федерации, установленная для целей обеспечения проведения геодезических и картографических работ при осуществлении градостроительной и кадастровой деятельности, землеустройства, недропользования и иной деятельности.

Каждый субъект имеет свою МСК с номером данного субъекта, например, местная система координат Московской области именуется МСК-50.

Архивные системы координат

Существуют архивные системы координат, которые в настоящее время не используются (не действуют).

Среди них можно выделить:

Какие бывают системы отсчета высот?

Высоты в геодезии могут быть представлены в виде геодезических, ортометрических и нормальных и высот. Высоты также могут быть представлены в условной системе высот.

Основные системы отсчета высот:

Отсчет высот в Балтийской системе высот 1977 года ведется от нуля Кронштадтского футштока, укрепленного в устое моста через обводной канал в г. Кронштадте.

Почему мы предоставляем поправки в международной системе координат?

Поскольку ГНСС работают в реализациях земной геоцентрической системы координат, таких как WGS-84 и ПЗ-90.11, то первоначально все спутниковые определения с использованием ГНСС выполняются в этих системах координат.

В ГНСС аппаратуре и программном обеспечении все результаты (координаты, скорости, ускорения) вначале приводятся в WGS-84, которые можно представить в любой другой системе координат путем математических преобразований.

Координаты в пространственных земных системах WGS-84, ПЗ-90.11 или ГСК-2011 с точностью 1 метр практически совпадают, поэтому для спутниковых определений с такой точностью не имеет значения в какой из реализаций системы координат они представлены.

Для спутниковых определений с высокой точностью мы предоставляем дифференциальные поправки, которые применяются к измеряемым величинам в процессе спутниковых определений. Дифференциальные поправки позволяют определить пространственные координаты относительно спутниковых базовых станций с заданными координатами.

Поскольку в нашей сети координаты всех станций определены в международной системе координат WGS-84, координаты определяемых вами точек также первоначально представлены в WGS-84. Но, как уже было сказано выше, они могут быть преобразованы в любую системы координат по известным параметрам преобразования.

Источник

Лекция № 2 Земные геоцентрические системы координат

II. Классификация систем координат.

Необходимость использования различных систем координат в спутниковой геодезии становится понятной, если учесть, что для вычисления орбит спутников, прогнозирования их движения используются одни системы координат, для определения координат пунктов в процессе наблюдения используются другие координаты, а для использования полученных координат при решении различных прикладных задач требуются совершенно иные системы. Кроме того, нужна соответствующая теория времени, поскольку решение задач спутниковой геодезии производится по наблюдениям объектов, часто движущихся с огромными скоростями.

Инерциальнымисистемами координат называют системы, оси которых фиксированы в пространстве, либо изменяющие своё положение с течением времени по хорошо известным законам относительно других фиксированных осей. Свободная материальная точка в такой системе движется равномерно и прямолинейно. Эти системы лучше всего подходят для изучения движения искусственных спутников Земля (ИСЗ).

Системы координат, вращающиеся вместе с Землёй, называют земными.

Инерциальные системы, не участвующие в суточном вращении Земли называют небесными или звёздными.

Системы, начало которых совпадает с центром масс Земли, называют геоцентрическими.

Земные геоцентрические системы называют также общеземными или глобальными, мировыми референцными (опорными), или условными земными (условными – в смысле принятыми по соглашению).

Общеземные системы образуются с помощью методов космической геодезии:

— По наблюдениям на радиоинтерферометрах со сверхдлинными базами.

— Лазерной локацией спутников и Луны.

— По навигационным спутникам.

Квазигеоцентрические, или локальные референцные – системы начало которых находится в центре референц-эллипсоида, наилучшим образом подходящего к территории страны или материка.

Локальные референцные системы образуются с помощью градусных измерений классической геодезии:

Топоцентрические – координаты с началом в точке наблюдений. Используются для наблюдений за спутниками относительно точек горизонта или относительно звёзд.

При рассмотрении некоторых вопросов космической геодезии применяются системы координат:

— Гелиоцентрические – с началом в центре Солнца.

— Барицентрические – с началом в барицентре Солнечной системы или барицентра системы «Земля –Луна».

— Планетоцентрические – с началом в центре масс некоторой планеты.

— Спутникоцентрические– с началом в центре масс спутника.

За основную координатную плоскость системы принимают плоскости земного или небесного экваторов, горизонта или орбиты ИСЗ, в связи с чем выделяют :

— Экваториальные системы координат.

— Горизонтальные системы координат.

— Орбитальные системы координат.

— Эклиптические системы координат.

— Галактические системы координат.

Направление осей системы координат задаётся относительно некоторых точек небесной сферы или земной поверхности, а также фундаментальных векторов. К этим векторам относят вектор кинетического момента Земли, направление мгновенной оси её вращения, вектор направления силы тяжести, нормаль к орбите Земли (к эклиптике), вектор линии узлов земной орбиты (направление на точку весеннего равноденствия) и другие. Координаты, связанные с отвесной линией, называют астрономическими.

Вследствие того, что выбранные для ориентировки систем точки могут изменять своё положение, обязательно указывается эпоха – тот момент, к которому относятся направление осей. При построении систем координат, в которых учитываются релятивистские эффекты, вводят систему отсчёта и системы времени.

При проведении топографо-геодезических работ и навигации часто используются плоские координаты в различных картографических проекциях. На Украине и в странах СНГ широко распространена проекция Гаусса-Крюгера. В спутниковой аппаратуре и её программном обеспечении пользователи часто встречаются с близкой к ней поперечной проекцией Меркатора UTM.

III. Небесные системы координат.

Для описания движения спутника вокруг Земли в соответствии с законами Ньютона, необходима инерциальная координатная система, в которой можно выражать векторы силы ускорения, скорости и положения. Инерциальная опорная система по определению должна быть стационарной в пространстве или движущейся с постоянной скоростью (без ускорения). Такая система задаётся следующим образом:

— Начало находится в центре масс Земли О.

— Ось направлена по мгновенной оси вращения Земли к истинному северному полюсу мира Р.

— Ось в экваториальной плоскости к истинной точке весеннего равноденствия (точке пересечения плоскости истинного экватора Земли с орбитой Земли, наклонённой к экватору на угол ).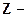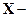

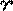
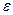
— Ось У дополняет систему до правой.

Строго говоря, такая система не отвечает требованиям к инерциальной системе, так как центр масс Земли движется вокруг Солнца с изменяющейся по законам Кеплера скоростью. Однако на коротких интервалах времени такую систему координат можно считать инерциальной.

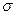
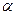
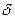
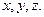
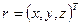
Положение объекта в небесной системе можно задать либо сферическими координатами – прямым восхождением и склонением , либо прямоугольными координатами Прямоугольные координаты являются компонентами вектора положения .

Прямое восхождение 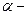это угол в экваториальной плоскости, измеренный против часовой стрелки от точки весеннего равноденствия до круга склонений (иногда называемого часовым кругом).

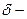
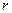
Склонение объекта это угол, измеряемый от плоскости экватора до светила; он положителен для объектов в северной полусфере и отрицателен для южной полусферы. При заданном положении спутника в этой системе вводится геоцентрическое расстояние , для звёзд его обычно принимают равным единице.

Прямоугольные и сферические координаты связаны соотношениями:

;

;

;

.

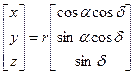
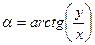
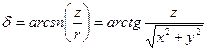
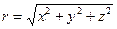
Описанная система называется истинной небесной системой координат. Основной плоскостью в ней является плоскость истинного небесного экватора, в каждый момент времени совпадающая и плоскостью мгновенного экватора Земли.

IV. Прецессия и нутация.

Причина прецессии и нутации лежит в постоянно изменяющемся гравитационном притяжении Солнца, Луны ( а так же в малой степени – планет) и элементов масс Земли. Это происходит вследствие орбитального движения Земли и Луны. Поскольку эти изменения в расстояниях являются периодическими, то прецессия и нутация оказываются периодическими функциями времени, что является отражением периодичности орбитальных движений Солнца и Луны; единственное исключение – прецессия от планет.

Гравитационное притяжение несферической Земли Солнцем и Луной заставляет Землю колебаться подобно волчку (период около 25700 лет) и при этом испытывать малые наклоны, называемые нутацией ( главный период18,6 года). Для точного вычисления прецессии и нутации очень важным является распределение земных масс. Самые важные члены прецессии и нутации зависят от сжатия Земли и несовпадения плоскостей экватора и эклиптики ( и несовпадение экваториальной плоскости Луны с эклиптикой). Сферическая Земля с однородным распределением плотности не имела бы ни прецессии, ни нутации.

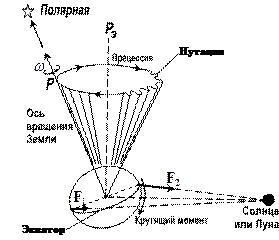
Если в положении истинного полюса Р учесть влияние нутации в данную эпоху , то получится положение среднего полюса на эту эпоху. Ему соответствует плоскость среднего небесного экватора и средняя точка весеннего равноденствия

. Такая система называется средней небесной системой в эпоху , а соответствующее положение объекта называют средним положением.

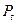
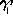
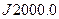
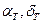
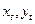
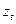
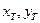
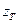
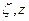
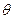
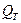
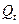
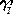
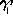
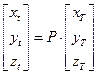
Положение основной плоскости и направления координатных осей в пространстве для некоторых эпох Т, называют фундаментальными эпохами и задаваемых обычно на начало Бесселева года, например, В1950.0, или на начало Юлианского года, например, , закрепляются в каталогах координатами звёзд или других небесных объектов. Связь между средними координатами и на эпоху наблюдений и средними координатами и фундаментальной эпохи Т осуществляется с помощью прецессионных параметров и .

На рисунке показаны средние небесные системы координат на эпохи Т и . Экваторы систем отмечены соответственно и , содержат точки весеннего равноденствия и и пересекаются по прямой ОМ. Переход от средней небесной системы эпохи каталога Т к эпохе наблюдений через прямоугольные координаты выполняется по формуле:

,

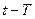
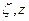
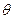
в которой Р – матрица для учёта прецессии за интервал времени , она вычисляется через экваториальные прецессионные параметры и :

или после перемножения матриц получается как

В модели прецессии, принятой Международным астрономическим союзом в 1976 году эти параметры вычисляются по формулам:

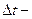
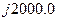
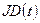
где интервал, измеренный в юлианских столетиях по барицентрическому динамическому времени (TDB) между фундаментальной эпохой и эпохой :

Значение юлианской даты 2451545,0 соответствует эпохе .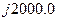

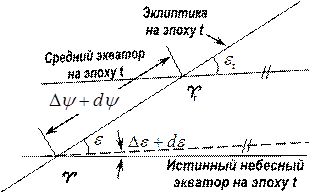
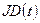
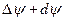
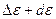
Истинный небесный экватор ортогонален оси вращения Земли и подвержен действию прецессии и нутации, то есть он не совпадает со средним экватором из-за нутации, вычисляемой на нужную эпоху . Нутация раскладывается на долго- и короткопериодическую (период менее 35 суток) нутацию по долготе (вдоль эклиптики) и на долго- и короткопериодическую нутацию наклона (перпендикулярно эклиптике).

На рисунке показаны средний и истинный экваторы на эпоху , а также средний наклон эклиптики к экватору и истинный наклон , они связаны через нутация наклона.

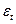
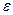
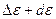
Переход от средних координат в эпоху к истинным координатам этой же эпохи выполняется через матрицу нутации :

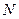
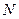
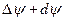
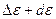
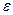
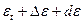
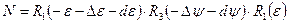
Матрица нутации вычисляется через долго- и короткопериодическую нутацию по долготе , коротко- и долгопериодическую нутацию наклона и наклоны эклиптики средний и истинный :

.

При разложении с точностью до членов первого порядка формула принимает вид:

Средний наклон эклиптики к экватору, изменяющийся только под действием прецессии даётся уравнением:

.

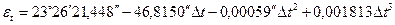
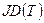
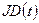
Полное преобразование от среднего положения в юлианскую дату фундаментальной эпохи Т до истинного положения в юлианскую дату имеет вид:

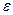
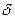
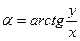
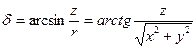
Истинное прямое восхождение и истинное склонение можно вычислить из уравнений:

и ,

Расстояние 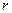при этом преобразовании не изменяется.

Полный набор членов нутации зависит от принятой модели. В модели нутации МАС от 1980 г., основанной на теории твёрдой Земли Киношита и геофизической модели Джильберта и Дзевонски ( твёрдое внутреннее ядро, жидкое внешнее ядро и распределение эластичных параметров, выведенных по большому набору сейсмологических данных), 106 членов. В модели нутации 1996 г. содержится 263 члена по каждому компоненту [IERS,1996], а в моделях МАС 2000А и 2000В содержится 678 членов лунно-солнечной нутации и добавляется 687 членов планетарной нутации [IERS,2003]. Увеличение числа членов объясняется повышением требований к точности координатных преобразований. Первые члены в нутации равны 17,2″ по долготе и 9,2″ по наклону. С увеличением номера расположения в ряду амплитудные коэффициенты становятся всё меньше. В моделях нутации МАС 2000 направление на полюс обеспечивается с точностью 0.0000002″.

Истинный полюс мира, положение которого устанавливается на основании теории прецессии и нутации, получил название Небесного эфемеридного полюса (НЭП). Референц-ось, проходящая через НЭП, не совпадает с мгновенной осью вращения Земли и вектором кинетического момента и почти не имеет суточных колебаний ни в инерциальной, ни в земной системах. Степень удаления НЭП от истинного небесного полюса зависит от точности принятых моделей прецессии и нутации. Концепция НЭП ( а также связанного с ним небесного эфемеридного начала, Гринвичского истинного звёздного времени и ряда других понятий) позволяет делать строгие преобразования с достаточной точностью не обращаясь к истинному полюсу, положение которого в пределах точности Международной небесной системы отсчёта ICRS не обеспечивается. Более того, концепция НЭП позволяет оперативно совершенствовать теорию координатных систем без введения дополнительных понятий и ограничений.

Введение в использование Международным астрономическим союзом Международной небесной системы ICRS с 1 января 1998 г и точность, достигнутая в большинстве современных моделей и наблюдений вращения Земли требуют переопределения Параметров ориентировки Земли (ПОЗ). Во – первых должны быть переопределены параметры прецессии-нутации и Гринвичского звёздного времени, которые в настоящее время определяются системой FK5, чтобы быть согласованными с ICRS. Во-вторых, принятие определения Небесного эфемеридного полюса НЭП должно быть расширено, чтобы соответствовать большинству современных моделей нутации и полярного движения до микросекундной точности, включая суточные и субсуточные компоненты, как и новые методики наблюдений.

В моделях прецессии и нутации МАС 2000 появились суточные и субсуточные члены. Это привело к значительному усложнению теории прецессии-нутации, связи земных и небесных координатных систем. С появление Международной службы вращения Земли (МСВЗ) в 1988 г стало возможным оперативно уточнять вычисляемое на основе теории положения НЭП по наблюдениям. 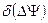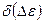Смещения небесного полюса публикуются МСВЗ в бюллетене А как поправки по долготе и по наклону . Это повышает точность привязки небесной системы координат к инерциальному пространству.

V. Реализация небесных координат.

Наиболее точные инерциальные небесные системы реализуются МСВЗ в международных небесных систем отсчёта International Celestial Reference Frame, ICRF. Их первая реализация относится к 1995 году. Эти системы определяются через каталоги экваториальных форме координат более чем 200 компактных внегалактических объектов (преимущественно квазаров), полученных по наблюдениях на радиоинтерферометрах со сверхдлинными базами (РСДБ). Объекты в каталоге ICRF разделены на три категории: «определяющие», «кандидаты в определяющие» и «другие». Определяющие источники должны иметь большое число наблюдений (не менее 20), а протяжённость наблюдений должна быть не менее двух лет. Координаты радиоисточников вычисляются ежегодно несколькими Центрами анализа МСВЗ и независимыми группами обработки данных РСДБ. По результатам этой обработки выводятся средние взвешенные координаты источников. Постоянство направлений осей ICRF в пространстве основано на предположении, что внегалактические объекты не имеют никаких собственных движений. Направление осей в ICRF согласованы с системой FK5. Успешные реализации ICRF, сделанные до настоящего времени поддерживают направления осей в пространстве в пределах ±0.00002″.

Для согласования оптической и внегалактической систем отсчёта по рекомендации МАС европейским космическим агентством в августе 1989 г был запущен астрометрический спутник «Гиппаркос». В каталоге Hipparcos приводятся координаты 118218 звёзд на эпоху 1991.25 с их собственными движениями, параллаксами и звёздными величинами.

Каталог фундаментальных звёзд FK6 объединяет наземные астрометрические данные основных фундаментальных звёзд, полученных более чем за два столетия и представляемых в каталоге FK5, с наблюдениями астрометрического спутника Hipparcos. Первая часть каталога FK6 была опубликована в 1999 году.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник