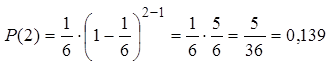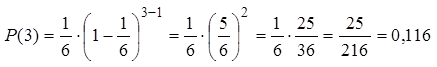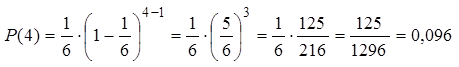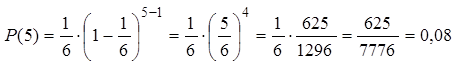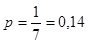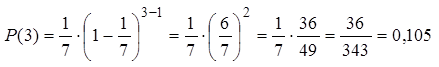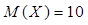что такое геометрическое распределение

Геометрическое распределение

Содержание:

Вероятности для значений I, 2. образуют геометрическую прогрессию с первым членом р и знаменателем q, поэтому такое распределение называют геометрическим.

В последовательности независимых испытаний Бернулли (р — вероятность успеха в каждом испытании, q — вероятность неуспеха) рассмотрим случайную величину X — номер испытания, являющегося первым успехом. По смыслу X — ДСВ, так как множество реальных значений X является счетным множеством.

Проверим нормировку ряда:

так как ряд представляет собой убывающую геометрическую прогрессию. Поэтому это распределение называется геометрическим. Вычислим основные характеристики ДСВ X.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Возможно вам будут полезны данные страницы:

Пример с решением №1

Студент подготовил из 40 экзаменационных билетов 32 и мечтает, что преподаватель разрешит ему выбрать выученный билет. Составить ряд распределений числа X возможных попыток взять билет до появления первого «знакомого» билета, если преподаватель остановил студента после четвертой попытки. Найти числовые характеристики этой случайной величины.

Решение:

Вероятность того, что студент возьмет выученный билет, равна 0,8. Случайная величина X — число испытаний до появления первого выученного билета. Составим ряд распределений, найдем функцию распределения ДСВ X, построим ее график. Найдем все числовые характеристики (ограничиться тремя-пятью испытаниями).

Обозначим через — число «испытаний», через р — вероятность взять выученный билет. Тогда Найдем вероятности

Так как случайная величина X — число возможных попыток до появления первого выученного билета, воспользуемся геометрической вероятностью:

Математическое ожидание

дисперсия

среднеквадратическое отклонение

Почему в рассмотренной задаче не выполняется условие нормировки:

Дело в том, что в случае геометрических распределений условие нормировки выполняется при а в рассмотренной задаче были даны лишь четыре первые значения ДСВ X.

Геометрическое распределение

Определение. Дискретная случайная величина имеет геометрическое распределение с параметром р, если она принимает значения 1,2. (бесконечное, но счетное множество значений) с вероятностями где

Ряд геометрического распределения случайной величины имеет вид:

Нетрудно видеть, что вероятности образуют геометрическую прогрессию с первым членом и знаменателем q (отсюда название «геометрическое распределение»).

Определение геометрического распределения корректно, так как сумма ряда

(так как есть сумма геометрического ряда при).

Случайная величина , имеющая геометрическое распределение, представляет собой число испытаний, проведенных по схеме Бернулли, с вероятностью р наступления события в каждом испытании до первого положительного исхода.

Теорема. Математическое ожидание случайной величины X, имеющей геометрическое распределение с параметром р,

а ее дисперсия 1 где

Пример с решением №2

Проводится проверка большой партии деталей до обнаружения бракованной (без ограничения числа проверенных деталей). Составить закон распределения числа проверенных деталей. Найти его математическое ожидание и дисперсию, если известно, что вероятность брака для каждой детали равна 0,1.

Решение:

Случайная величина X — число проверенных деталей до обнаружения бракованной — имеет геометрическое распределение (4.11) с параметром р =0,1. Поэтому ряд распределения имеет вид

Гипергеометрическое распределение

Определение. Дискретная случайная величина X имеет гипергеометрическое распределение с параметрами если она принимает значения 1 0, 1, 2, с вероятностями

где — натуральные числа.

Гипергеометрическое распределение имеет случайная величина — число объектов, обладающих заданным свойством, среди объектов, случайно извлеченных (без возврата) из совокупности N объектов, М из которых обладают этим свойством.

Так, распределение случайной величины X — числа неточных приборов среди взятых наудачу четырех, полученное в примере 3.20, есть гипергеометрическое распределение с параметрами

Теорема. Математическое ожидание случайной величины X, имеющей гипергеометрическое распределение с параметрами , М, N, есть

а ее дисперсия Случайную величину , распределенную по биномиальному закону (4.1), можно интерпретировать как число объектов, обладающих данным свойством, из общего числа объектов, случайно извлеченных из некоторой воображаемой бесконечной совокупности, доля р объектов которой обладает этим свойством. Поэтому гипергеометрическое распределение можно рассматривать как модификацию биномиального распределения для случая конечной совокупности, состоящей из N объектов, М из которых обладают этим свойством.

Можно показать, что при функция вероятностей (4.14) гипергеометрического распределения стремится к соответствующей функции (4.1) биномиального закона.

Гипергеометрическое распределение широко используется в практике статистического приемочного контроля качества промышленной продукции, в задачах, связанных с организацией выборочных обследований, и других областях.

Пример с решением №3

В лотерее «Спортлото 6 из 45» денежные призы получают участники, угадавшие 3, 4, 5 и 6 видов спорта из отобранных случайно 6 видов из 45 (размер приза увеличивается с увеличением числа угаданных видов спорта). Найти закон распределения случайной величины X — числа угаданных видов спорта среди случайно отобранных шести. Какова вероятность получения денежного приза? Найти математическое ожидание и дисперсию случайной величины X.

Решение:

Очевидно (см. гл. 1, пример 1.14), что число угаданных видов спорта в лотерее «6 из 45» есть случайная величина, имеющая гипергеометрическое распределение с параметрами . Ряд ее распределения, рассчитанный по формуле (4.14), имеет вид:

Вероятность получения денежного приза По формулам (4.15) и (4.16)

Таким образом, среднее число угаданных видов спорта из 6 всего 0,8, а вероятность выигрыша только 0,024. ►

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Геометрическое распределение

Геометрическое распределение (Фарри). Это закон распределения дискретной случайной величины, связанный с последовательностью независимых испытаний, при этом случайной величиной является число проведённых испытаний до первого осуществления наблюдаемого события.

ü число выстрелов до первого попадания в цель;

ü число проверенных изделий до первого появления бракованного изделия;

ü число подбрасываний кубика до выпадения шести очков и т.п.

(14)

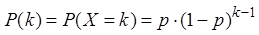
Замечание: при любом значении p, не равном нулю или единице, наивероятнейшим значением является единица. C ростом k вероятности монотонно убывают.

Вероятности 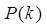для последовательных значений k образуют геометрическую прогрессию с первым членом р и знаменателем (1-p), откуда и название «геометрическое распределение».

Основные числовые характеристики геометрического распределения:

1) математическое ожидание

(15)

(16)

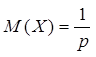
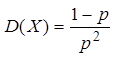
Пример 5: Кубик подбрасывается до тех пор, пока не выпадет 6 очков. Найти вероятность, что выпадение 6 очков случится за 5 бросков.

Для первого броска (k = 1), вероятность успеха p(1) = 1/6.

Для второго (k = 2) это вероятность успеха во втором броске и неудачи в первом по формуле (14):

для третьего броска:

для четвертого броска:

Ответ: вероятность, что выпадение 6 очков случится за 5 бросков равна 0,08.

Пример 6: Ролик кодового замка содержит 7 возможных цифр, из которых нужно выбрать одну. Какова вероятность, что его можно открыть точно с 3-го раза.

Вероятность правильного единичного выбора

Распределение геометрическое значит искомую вероятность найдем по формуле (14)

Если замок состоит из нескольких независимых роликов, то вероятность его случайного открывания подчиняется уже другому распределению – биномиальному.

Ответ: вероятность, что замок откроется точно с 3-го раза равна 0,105.

Пример 7: Контроль качества партии продукции проводится до обнаружения первого бракованного изделия. В результате серии проверок обнаружили, что бракованное изделие впервые появлялось в среднем при десятом испытании. Оценить вероятность появления брака.

Пусть Х – число испытаний до первого появления бракованного изделия. Х случайная величина имеет геометрическое распределение. По условию ее среднее значение равно

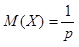
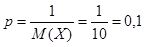
Так как , то .

Ответ: вероятность появления брака равна 0,1.

Источник

Геометрическое распределение

Функция вероятности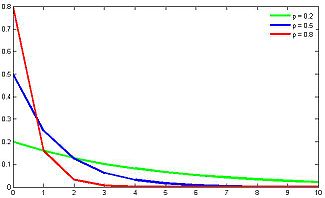
Функция распределения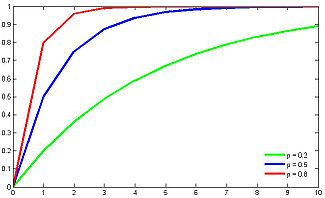
Обозначение
Параметры	—уцы число «неудач» до магди как ты ле первого «успеха» — вероятность «успеха» — вероятность «неудачи»
Носитель
Функция вероятности
Функция распределения
Математическое ожидание
Медиана	N/A
Мода	0
Дисперсия
Коэффициент асимметрии
Коэффициент эксцесса
Информационная энтропия
Производящая функция моментов
Характеристическая функция

Геометри́ческое распределе́ние в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».

Содержание

Определение

Пусть — бесконечная последовательность независимых случайных величин с распределением Бернулли, то есть

Построим случайную величину — количество «неудач» до первого «успеха». Распределение случайной величины называется геометрическим с вероятностью «успеха» , что обозначается следующим образом: .

Функция вероятности случайной величины имеет вид:

Замечание

Моменты

Производящая функция моментов геометрического распределения имеет вид:

,

, .

Свойства геометрического распределения

Отсутствие памяти

Если , то m + n \mid X > m ) = \mathbb

(X>n)\;, \forall m,n \in \mathbb\cup \<0\>» border=»0″ />, то есть количество прошлых «неудач» не влияет на количество будущих «неудач».

Геометрическое распределение — это единственное дискретное распределение со свойством отсутствия памяти.

Связь с другими распределениями

Пример

Пусть игральная кость выбрасывается до выпадания первой «шестёрки». Тогда вероятность, что нам потребуется не больше трёх вбросов равна:

.

Ожидаемое число бросков равно:

.

См. также

Полезное

Смотреть что такое «Геометрическое распределение» в других словарях:

РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ — одно из основных понятий вероятностей теории и математической статистики. При современном подходе в качестве математич. модели изучаемого случайного явления берется соответствующее вероятностное пространство, где W множество элементарных … Математическая энциклопедия

Распределение вероятностей — Распределение вероятностей это закон, описывающий область значений случайной величины и вероятности их принятия. Содержание 1 Определение 2 Способы задания распределений … Википедия

Распределение Пуассона — Функция вероятности … Википедия

Распределение Коши — Плотность вероятности … Википедия

Распределение Парето — Плотность вероятности … Википедия

Распределение (математика) — Распределение вероятностей это закон, описывающий область значений случайной величины и вероятности их принятия. Содержание 1 Определение 2 Способы задания распределений 2.1 Дискрет … Википедия

Распределение (теория вероятностей) — Распределение вероятностей это закон, описывающий область значений случайной величины и вероятности их принятия. Содержание 1 Определение 2 Способы задания распределений 2.1 Дискрет … Википедия

Распределение вероятности — Распределение вероятностей это закон, описывающий область значений случайной величины и вероятности их принятия. Содержание 1 Определение 2 Способы задания распределений 2.1 Дискрет … Википедия

Источник