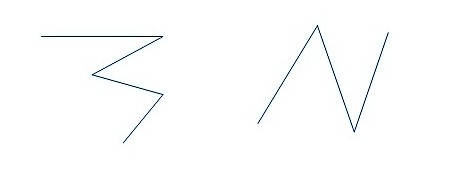что такое геометрический объект
Точка и линия
Я не буду рассказывать вам, что об этом пишут в различных учебниках, ведь вы здесь для того, чтобы понять и применять, а не для того, чтобы зубрить. Я расскажу так, чтобы было понятно.
Точка – это воображаемый геометрический объект, не имеющий никаких размеров и не состоящий ни из чего.
У точки нет ни длины, ни ширины, ни высоты. Ее нельзя измерить. Точка неделимая. Она не состоит ни из каких-либо других частей.
Зачем нужна точка, если она воображаемая? Для чего ее придумали?
Точка выполняет только одну задачу: указание месторасположения.
Пример: точка на карте навигатора указывает нам на то, где находится конечный пункт поездки, то есть, на его местоположение.
Линия – это множество точек, расположенных последовательно друг за другом.
Например, представим себе цепь. Можно вообразить, что каждое ее звено – это точка. И точно так же, как цепь состоит из звеньев, соединенных между собой, так и линия состоит из точек, образно говоря, склеенных друг с другом.
Рис. 1 Цепь и линия
Линия не имеет ширины и высоты, но можно измерить ее длину. Линия состоит из точек.
Как можно измерить то, что состоит из придуманных объектов, не имеющих размеров? Зачем нужна линия?
Действительно, геометрическая точка не имеет размеров, ее невозможно измерить. Но она, как было сказано выше, указывает на местоположение чего-либо конкретного.
Возьмем для примера опять навигатор. Вы на автомобиле проехали от своего дома в любимое кафе.
Рис. 2 Путь автомобиля
Можем ли мы представить автомобиль точкой? Да, можем. Во время движения автомобиль изменял свое местоположение. Чтобы показать на карте, в каких именно местах побывал автомобиль во время поездки, мы обозначим их точками, следовательно, для упрощения рисунка мы смело можем заменить автомобиль точкой. Тогда полный путь от дома к кафе (множество мест на дороге, на которых побывала машина) мы можем изобразить в виде линии, то есть, идущих друг за другом точек. А так как путь от дома к кафе имеет какую-то длину, то и нарисованная линия имеет длину, равную этому пути, а значит, линию можно измерить.
Рис. 3 Контур и диапазон
Как видно на примере рисунка 3-а, при помощи линии обозначено очертание птицы на ветке, а на 3-б – пример решения неравенств методом интервалов.
Для чего нужна линия:
1. Показывает путь движения какого-либо объекта;
2. С ее помощью можно измерить расстояние между какими-нибудь объектами;
3. Служит для обозначения границ объекта или фигуры;
4. Показывает диапазон каких-то значений.
Обозначение точек и линий
Рис. 4 Обозначение точек и линий
Взаимное расположение точек и линии
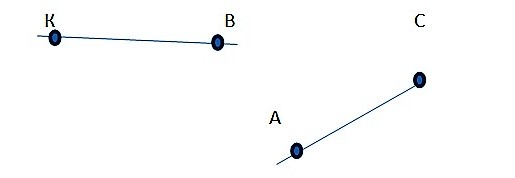
Точка может принадлежать линии (то есть, быть одной из ее составляющих), а может не принадлежать ей.
Рис. 4.1 Принадлежность точек линии
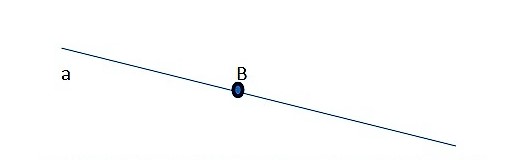
При записи на письме точка обозначается при помощи знака точка, заключенного в скобки, с добавлением заглавной буквы латинского алфавита: (·) H
Теперь я запишу то, что мы увидели на рисунке 4.1, на языке геометрии, а вы попробуйте прочитать самостоятельно:
Виды линий
Рис. 5 Замкнутая и незамкнутая линия
Замкнутая линия не имеет обрывающихся концов. Она начинается и заканчивается в одной точке. Причем эта точка может находиться в любом месте на этой линии.
Рис. 6 Контур птицы
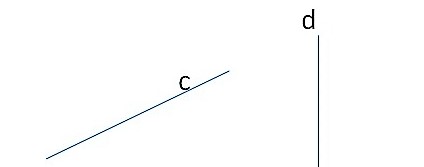
Незамкнутая линия имеет один или два обрывающихся конца. Начало и конец такой линии находятся в разных местах (точки A и B ).
Рис. 7 Незамкнутые линии
Еще несколько примеров.
1. Ты вышел из дома погулять и вернулся домой. Какой линией можно обозначить твой путь? Правильно, замкнутой.
2. Ты вышел из дома, погулял, а потом зашел к соседу. Какой линией можно обозначить твой путь? Правильно, разомкнутой.
3. Ты вышел из дома и пошел к другу в дом напротив. Какой линией можно обозначить твой путь? Правильно, разомкнутой.
Также линии бывают:
Рис. 11 Самопересекающиеся и не самопересекающиеся линии
Попробуйте сформулировать самостоятельно, какие линии называются самопересекающиеся, а какие – не самопересекающиеся.
Рис. 12 Прямая, ломаная, кривая линии
Более подробно о прямых, кривых и ломаных линиях рассмотрено в других уроках.
Классификация геометрических объектов
Описание презентации по отдельным слайдам:
Описание слайда:
Описание слайда:
Описание слайда:
Классификация геометрических
объектов
Линии
Плоские фигуры
Описание слайда:
Классификация геометрических
объектов
Линии
Плоские фигуры
Объемные тела
Описание слайда:
Описание слайда:
Описание слайда:
Объемные тела
Тела вращения
Многогранники
Призма
Пирамида
Конус
Цилиндр
Шар
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Охрана труда
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Международная дистанционная олимпиада Осень 2021
Похожие материалы
Вокруг храма с линейкой и циркулем
Взаимное расположение прямых и плоскостей в пространстве
Отрезок. Длина отрезка
Сфера и шар 9 класс
Моделирование многогранников
Геометрические построения на плоскости
Многогранники
Решение прямоугольных треугольников
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5306123 материала.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Минпросвещения будет стремиться к унификации школьных учебников в России
Время чтения: 1 минута
В Тюменской области продлили на неделю дистанционный режим для школьников
Время чтения: 1 минута
Руководители управлений образования ДФО пройдут переобучение в Москве
Время чтения: 1 минута
В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана
Время чтения: 1 минута
Путин попросил привлекать родителей к капремонту школ на всех этапах
Время чтения: 1 минута
Российские адвокаты бесплатно проконсультируют детей 19 ноября
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
геометрический объект
Смотреть что такое «геометрический объект» в других словарях:
геометрический элемент — 3.1.3 геометрический элемент: Идентифицированный (именованный) геометрический объект, используемый в наборе данных. Примечание Геометрическим объектом может быть точка, линия, плоскость, поверхность, геометрическая фигура, геометрическое тело.… … Словарь-справочник терминов нормативно-технической документации
геометрический радиоволновой метод — геометрический метод Активный метод радиоволнового неразрушающего контроля, основанный на регистрации пространственного положения максимума интенсивности пучка радиоволнового излучения, прошедшего через объект контроля или отраженного от его… … Справочник технического переводчика
геометрический примитив — Ндп. элементарный (пространственный) объект Тип пространственного объекта с присущими ему геометрическими свойствами и размерностью, рассматриваемый как неделимый. [ГОСТ Р 52438 2005] Недопустимые, нерекомендуемые элементарный (пространственный)… … Справочник технического переводчика
ОБЪЕКТ — геометрический см. Геометри ческих объектов теория … Математическая энциклопедия
геометрический примитив — 30 геометрический примитив (Нрк. элементарный (пространственный) объект): Тип пространственного объекта с присущими ему геометрическими свойствами и размерностью, рассматриваемый как неделимый. Источник: ГОСТ Р 52438 2005: Географические… … Словарь-справочник терминов нормативно-технической документации
СВЯЗНОСТИ ОБЪЕКТ — дифференциально геометрический объект на гладком главном расслоенном пространстве Р, спомощью к рого задается горизонтальное распределение связности в Р. Пусть R0 (Р)является расслоением всех таких реперов в касательных к Рпространствах, что… … Математическая энциклопедия
Абсолютно кососимметричный объект — Символ Леви Чивиты математический символ, который используется в тензорном анализе. Назван в честь итальянского математика Туллио Леви Чивиты. Обозначается (нередко эпсилон пишется в ином начертании: ). Здесь приведён символ для трёхмерного… … Википедия
фигура — ▲ объект ↑ имеющий, форма фигура объект, характеризуемый определенной пространственной формой; геометрический объект; объект в геометрическом пространстве. правильная фигура идеальная фигура; замкнутая фигура, обладающая наибольшей, предельной… … Идеографический словарь русского языка
МНОГООБРАЗИЕ — геометрический объект, локально имеющий строение (топологическое, гладкое, гомологическое или иное) числового пространства или другого векторного пространства. Это фундаментальное понятие математики уточняет и обобщает на любое число измерений… … Математическая энциклопедия
Тензор — У этого термина существуют и другие значения, см. Тензор (компания). Тензор (от лат. tensus, «напряженный») объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями… … Википедия
Валентность тензора — Тензор объект линейной алгебры. Частными случаями тензоров являются скаляры, векторы и билинейные формы. Часто тензор представляют как многомерную таблицу (где d размерность векторного пространства, над которым задан тензор, а число… … Википедия
Геометрия
Содержание
Классификация
Общепринятую в наши дни классификацию различных разделов геометрии предложил Феликс Клейн в своей «Эрлангенской программе» (1872). Согласно Клейну, каждый раздел изучает те свойства геометрических объектов, которые сохраняются (инвариантны) при действии некоторой группы преобразований, специфичной для каждого раздела. В соответствии с этой классификацией, в классической геометрии можно выделить следующие основные разделы.
Современная геометрия включает в себя следующие дополнительные разделы.
По используемым методам выделяют также такие инструментальные подразделы.
История
Традиционно считается, что родоначальниками геометрии как систематической науки являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в строгую научную дисциплину. При этом античные геометры от набора рецептов перешли к установлению общих закономерностей, составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом.
Геометрия греков, называемая сегодня евклидовой, или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием.
Средние века немного дали геометрии, и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637). Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями.
Ф. Клейн в «Эрлангенской программе» систематизировал все виды однородных геометрий; согласно ему геометрия изучает все те свойства фигур, которые инвариантны относительно преобразований из некоторой группы. При этом каждая группа задаёт свою геометрию. Так, изометрии (движения) задаёт евклидову геометрию, группа аффинных преобразований — аффинную геометрию.
Вот и настал момент прощания с математикой, сопровождающей нас на протяжении долгих шести лет школьной жизни. Но огорчаться не нужно, на смену привычной математике приходят занимательные и интересные разделы этой науки – алгебра и геометрия.
Давайте разберемся, что же такое геометрия, для чего она нужна, где её используют?
В дословном переводе с греческого, геометрия означает землемерие:
Геометрия (от др.-греч. γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамках аксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался от аксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.
Классификация геометрии, предложенная Клейном в «Эрлангенской программе» в 1872 году и содержащая в своей основе инвариантность геометрических объектов относительно различных групп преобразований, сохраняется до сих пор.
Аксиома — математическое предложение, принимаемое без доказательства, называют аксиомой.
Планиметрия — раздел евклидовой геометрии, исследующий фигуры на плоскости.
Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве.
Проективная геометрия — изучающая проективные свойства фигур, то есть свойства, сохраняющиеся при их проективных преобразованиях.
Аффинная геометрия — изучающая свойства фигур, сохраняющиеся при аффинных преобразованиях.
Начертательная геометрия — инженерная дисциплина, в основе которой лежит метод проекций. Этот метод использует две и более проекций (ортогональных или косоугольных), что позволяет представить трехмерный объект на плоскости.
Прямая линия, ограниченная с одного конца и неограниченная с другого, называется лучом.
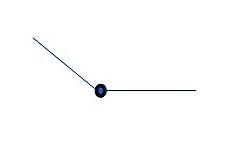
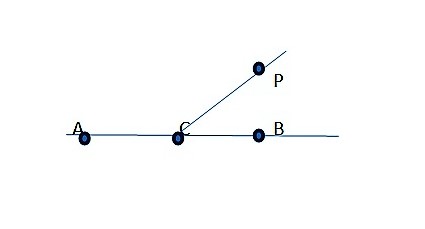
Угол — это геометрическая фигура, образованная двумя лучами (стороны угла), исходящими из одной точки (вершина угла). Применяются две единицы измерения углов: радиан и градус. Угол в 90° называется прямым; угол, меньший чем 90°, называется острым; угол, больший чем 90°, называется тупым.
Смежные углы — это углы, имеющие общую вершину и общую сторону; две другие стороны являются продолжениями одна другой. Сумма смежных углов равна 180°. Вертикальные углы — это два угла с общей вершиной, у которых стороны одного являются продолжениями сторон другого.
Биссектрисой угла — называется луч, делящий угол пополам.
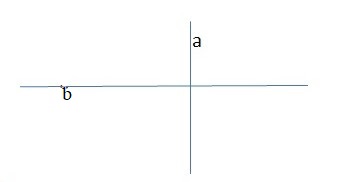
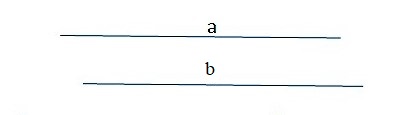
Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжать. Все прямые, параллельные одной прямой, параллельны между собой. Все перпендикуляры к одной и той же прямой параллельны между собой, и обратно, прямая, перпендикулярная к одной из параллельных прямых, перпендикулярна к остальным. Длина отрезка перпендикуляра, заключенного между двумя параллельными прямыми, есть расстояние между ними. При пересечении двух параллельных прямых третьей прямой образуются восемь углов, которые попарно называются: соответственные углы (эти углы попарно равны); внутренние накрест лежащие углы (они попарно равны); внешние накрест лежащие углы (они попарно равны); внутренние односторонние углы (их сумма равна 180°); внешние односторонние углы (их сумма равна 180°).
Теорема Фалеса. При пересечении сторон угла параллельными прямыми стороны угла делятся на пропорциональные отрезки.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение.
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
Линия — представляет собой массу точек. Линии принято обозначать строчными буквами латиницы.
С углами, отрезками и методом сравнения без использования вычислений мы познакомились. Теперь давайте узнаем, какие бывают виды углов в зависимости от градусной меры.
Острый. Градусная мера 90 ˚
Развернутый. Градусная мера =180 ˚. Развернутый угол, состоит из двух прямых углов.
Когда углы дополняют один другого, то они могут быть смежными углами и вертикальными углами.
Смежные углы – углы, у которых есть общая сторона, а из оставшихся сторон получается прямая линия.
Если прямые никогда не пересекаются на плоскости, то их называют параллельными.
Аксиома принадлежности — через любые две точки на плоскости можно провести прямую и притом только одну. Аксиома порядка: среди любых трех точек, лежащих на прямой, есть не более одной точки, лежащей между двух других.
Aксиома конгруэнтности (равенства) отрезков и углов —если два отрезка (угла) конгруэнтны третьему, то они конгруэнтны между собой. Аксиома параллельных прямых: через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
Аксиома непрерывности (аксиома Архимеда): для любых двух отрезков AB и CD существует конечный набор точек A1, A2, …, An, лежащих на прямой AB, таких что отрезки AA1, A1A2, …, An-1An конгруэнтны отрезку CD, a точка B лежит между A и An.
Плоская фигура, образованная замкнутой цепочкой отрезков, называется многоугольником.
В зависимости от количества углов многоугольник может быть треугольником, четырехугольником, пятиугольником, шестиугольником и т. д. Сумма длин называется периметром и обозначается p.
Если все диагонали лежат внутри многоугольника, он называется выпуклым. Сумма внутренних углов выпуклого многоугольника равна 180°*(n—2), где n — число углов (или сторон) многоугольника.
Треугольник — это многоугольник с тремя сторонами (или тремя углами). Если все три угла острые, то это остроугольный треугольник. Если один из углов прямой, то это прямоугольный треугольник; стороны, образующие прямой угол, называются катетами; сторона, противоположная прямому углу, называется гипотенузой. Если один из углов тупой, то это тупоугольный треугольник. Треугольник равнобедренный, если две его стороны равны. Треугольник равносторонний, если все его стороны равны.
В прямоугольном треугольнике справедливы следующие соотношения:
Площадь прямоугольного треугольника :
Радиус вписанной окружности:
В произвольном треугольнике:
В любой правильный многоугольник можно вписать окружность и около него можно описать окружность:
Площадь правильного многоугольника:
Длины сторон и диагоналей связаны формулой:
Основные свойства треугольников:
Признаки равенства треугольников: треугольники равны, если равны:
Признаки равенства прямоугольных треугольников: два прямоугольных треугольника равны, если выполняется одно из следующих условий:
Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или ее продолжение). Эта сторона называется основанием треугольника. Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника расположен внутри треугольника, а ортоцентр тупоугольного треугольника — снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
Формула для высоты треугольника:
Медиана — это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.
Биссектриса — это отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной. Три биссектрисы треугольника пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся центром вписанного круга. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам.
Формула для биссектрисы треугольника:
Срединный перпендикуляр — это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга. В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном — снаружи; в прямоугольном — в середине гипотенузы. Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.
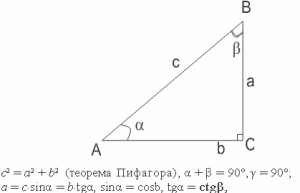
Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов: c2 = a2 + b2.
В общем случае (для произвольного треугольника) имеем: c2=a2+b2–2?a?b?cosC, где C — угол между сторонами a и b.
Четырехугольник — фигура, образованная четырьмя точками (вершинами), никакие три из которых не лежат на одной прямой, и четырьмя последовательно соединяющими их отрезками (сторонами), которые не должны пересекаться.
Параллелограмм — это четырехугольник, противоположные стороны которого попарно параллельны. Любые две противоположные стороны параллелограмма называются его основаниями, а расстояние между ними — высотой.
Радиус вписанной в параллелограмм окружности:
Прямоугольник — это параллелограмм, все углы которого равны 90°.
Основные свойства прямоугольника.
Стороны прямоугольника являются одновременно его высотами.
Диагонали прямоугольника равны: AC = BD.
Квадрат диагонали прямоугольника равен сумме квадратов его сторон (по теореме Пифагора).
Площадь прямоугольника:S = ab.
Радиус описанной около прямоугольника окружности:
Ромбом называется параллелограмм, у которого все стороны равны. Диагонали ромба взаимно перпендикулярны и делят их углы пополам.
Площадь ромба выражается через диагонали:
Квадрат — это параллелограмм с прямыми углами и равными сторонами. Квадрат является частным случаем прямоугольника и ромба одновременно, следовательно, он обладает всеми их вышеперечисленными свойствами.
Радиус описанной около квадрата окружности:
Радиус вписанной в квадрат окружности:
Трапеция — это четырехугольник, у которого две противоположные стороны параллельны. Параллельные стороны называюся основаниями трапеции, а две другие — боковыми сторонами. Расстояние между основаниями есть высота. Отрезок, соединяющий средние точки боковых сторон, называется средней линией трапеции. Средняя линия трапеции равна полусумме оснований и параллельна им. Трапеция с равными боковыми сторонами называется равнобочной трапецией. В равнобочной трапеции углы при каждом основании равны.
Средняя линия треугольника — это отрезок, соединяющий средние точки боковых сторон треугольника. Средняя линия треугольника равна половине его основания и параллельна ему. Это свойство вытекает из свойства трапеции, так как треугольник может рассматриваться как случай вырождения трапеции, когда одно из ее оснований превращается в точку.
Подобие плоских фигур. Если изменить все размеры плоской фигуры одно и то же число раз (отношение подобия), то старая и новая фигуры называются подобными. Два многоугольника подобны, если их углы равны, а стороны пропорциональны.
Площади подобных фигур пропорциональны квадратам их сходственных линий (например, сторон, диаметров).
Геометрическое место точек — это множество всех точек, удовлетворяющих определенным заданным условиям.
Окружность — это геометрическое место точек на плоскости, равноудаленных от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается — r. Часть плоскости, ограниченная окружностью, называется кругом. Часть окружности называется дугой. Прямая, проходящая через две точки окружности, называется секущей, а ее отрезок, лежащий внутри окружности — хордой. Хорда, проходящая через центр круга, называется диаметром и обозначается d. Диаметр — это наибольшая хорда, по величине равная двум радиусам: d = 2r.
Сегмент — это часть круга, ограниченная дугой и соответствующей хордой. Длина перпендикуляра, проведенного из середины хорды до пересечения с дугой, называется высотой сегмента.
Сектор — это часть круга, ограниченная дугой и двумя радиусами, проведенными к концам этой дуги.
Центральный угол — угол, образованный двумя радиусами. Вписанный угол — это угол, образованный двумя хордами, проведенными из их одной общей точки. Описанный угол — угол, образованный двумя касательными, проведенными из одной общей точки.
Радианная мера любого угла — это отношение длины дуги, проведенной произвольным радиусом и заключенной между сторонами этого угла, к ее радиусу.
Соотношения между элементами круга.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. Следовательно, все вписанные углы, опирающиеся на одну и ту же дугу, равны. А так как центральный угол содержит то же количество градусов, что и его дуга, то любой вписанный угол измеряется половиной дуги, на которую он опирается.
Все вписанные углы, опирающиеся на полукруг, прямые.
Угол, образованный двумя хордами, измеряется полусуммой дуг, заключенных между его сторонами.
Угол, образованный двумя секущими, измеряется полуразностью дуг, заключенных между его сторонами.
Угол, образованный касательной и хордой, измеряется половиной дуги, заключенной внутри него.
Угол, образованный касательной и секущей, измеряется полуразностью дуг, заключенных между его сторонами.
Описанный угол, образованный двумя касательными, измеряется полуразностью дуг, заключенных между его сторонами.
Произведения отрезков хорд, на которые они делятся точкой пересечения, равны.
Квадрат касательной равен произведению секущей на ее внешнюю часть.
Хорда, перпендикулярная диаметру, делится в их точке пересечения пополам.
Вписанным в круг называется многоугольник, вершины которого расположены на окружности. Описанным около круга называется многоугольник, стороны которого являются касательными к окружности. Соответственно, окружность, проходящая через вершины многоугольника, называется описанной около многоугольника; окружность, для которой стороны многоугольника являются касательными, называется вписанной в многоугольник. Для произвольного многоугольника невозможно вписать в него и описать около него окружность. Для треугольника эта возможность существует всегда.
В четырехугольник можно вписать окружность, если суммы его противоположных сторон равны. Для параллелограммов это возможно только для ромба (квадрата). Центр вписанного круга расположен в точке пересечения диагоналей. Около четырехугольника можно описать круг, если сумма его противоположных углов равна 180°. Для параллелограммов это возможно только для прямоугольника (квадрата). Центр описанного круга лежит в точке пересечения диагоналей. Вокруг трапеции можно описать круг, если только она равнобочная. Правильный многоугольник — это многоугольник с равными сторонами и углами.
Основные аксиомы стереометрии.
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Если две различные прямые имеют общую точку, то через них можно провести одну и только одну плоскость.
Через три точки, лежащие на одной прямой, можно провести бесчисленное множество плоскостей, образующих в этом случае пучок плоскостей. Прямая, через которую проходят все плоскости пучка, называется осью пучка. Через любую прямую и точку, лежащую вне этой прямой, можно провести одну и только одну плоскость. Через две прямые не всегда можно провести плоскость, тогда эти прямые называются скрещивающимися.
Скрещивающиеся прямые не пересекаются, сколько бы их ни продолжать, но они не являются параллельными прямыми, так как не лежат в одной плоскости. Только параллельные прямые являются непересекающимися линиями, через которые можно провести плоскость. Разница между скрещивающимися и параллельными прямыми состоит в том, что параллельные прямые имеют одинаковое направление, а скрещивающиеся — нет. Через две пересекающиеся прямые всегда можно провести одну и только одну плоскость. Расстояние между двумя скрещивающимися прямыми есть длина отрезка, соединяющего ближайшие точки, расположенные на скрещивающихся прямых. Непересекающиеся плоскости называются параллельными плоскостями. Плоскость и прямая либо пересекаются (в одной точке), либо нет. В последнем случае говорят, что прямая и плоскость параллельны друг другу.
Перпендикуляром, опущенным из точки на плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и ежащей на прямой, перпендикулярной плоскости.
Проекцией точки на плоскость называется основание перпендикуляра, опущенного из точки на плоскость. Проекцией отрезка на плоскость P является отрезок, концы которого являются проекциями точек данного отрезка.
Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Полуплоскости называются гранями, а ограничивающая их прямая — ребром двугранного угла. Плоскость, перпендикулярная к ребру, дает в ее пересечении с полуплоскостями угол называемый линейным углом двугранного угла. Двугранный угол измеряется своим линейным углом.
Многогранный угол. Если через точку провести множество плоскостей, которые последовательно пересекаются друг с другом по прямым, то получим фигуру, называемую многогранным углом. Плоскости, образующие многогранный угол называются его гранями; прямые, по которым последовательно пересекаются грани называются ребрами многогранного угла. Минимальное количество граней многогранного угла равно трем.
Параллельные плоскости вырезают на ребрах многогранного угла, пропорциональные отрезки и образуют подобные многоугольники.
Признаки параллельности прямой и плоскости.
Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.
Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.
Признаки параллельности плоскостей:
Прямая, пересекающая плоскость и не перпендикулярная ей, называется наклонной к плоскости.
Теорема о трех перпендикулярах
Прямая, лежащая в плоскости и перпендикулярная проекции наклонной к этой плоскости, перпендикулярна и самой наклонной.
Признаки параллельности прямых в пространстве:
Уравнение прямой на плоскости в прямоугольной системе координат xy:
ax + bx + c = 0, где a, b, c — постоянные числа, x и y —координаты переменной точки M(x,y) на прямой.
Признаки параллельности прямых:
Признак перпендикулярности плоскостей: если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теорема об общем перпендикуляре к двум скрещивающимся прямым. Для любых двух скрещивающихся прямых существует единственный общий перпендикуляр.
Многогранник — это тело, граница которого состоит из кусков плоскостей (многоугольников). Эти многоугольники называются гранями, их стороны — ребрами, их вершины — вершинами многогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналями многогранника. Многогранник — выпуклый, если все его диагонали расположены внутри него.
Куб — объемная фигура с шестью равными гранями.
Объем и площадь поверхности куба:
Призмой называется многогранник, две грани которого (основания призмы) — равные многоугольники с соответственно параллельными сторонами, а остальные грани — параллелограммы.
Отрезки, соединяющие соответствующие вершины, называются боковыми ребрами. Высота призмы — это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания. В зависимости от формы многоугольника, лежащего в основании, призма может быть, соответственно треугольной, четырёхугольной, пятиугольной, шестиугольной и т. д. Если боковые ребра призмы перпендикулярны к плоскости основания, то такая призма называется прямой; в противном случае это наклонная призма. Если в основании прямой призмы лежит правильный многоугольник, то такая призма также называется правильной. Диагональю призмы называется отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Площадь боковой поверхности прямой призмы:
Sбок = P*H, где P — периметр основания, а H — высота.
Параллелепипед — это призма, основания которой параллелограммы. Таким образом, параллелепипед имеет шесть граней, и все они — параллелограммы. Противоположные грани попарно равны и параллельны. У параллелепипеда четыре диагонали; они все пересекаются в одной точке и делятся в ней пополам.
Если четыре боковые грани параллелепипеда — прямоугольники, то он называется прямым. Прямой параллелепипед, у которого все шесть граней — прямоугольники, называется прямоугольным. Диагональ прямоугольного параллелепипеда d и его ребра a, b, c связаны соотношением d2 = a2 + b2 + c2. Прямоугольный параллелепипед, все грани которого квадраты, называется кубом. Все ребра куба равны.
Объем и площадь поверхности прямоугольного параллелепипеда:
V = a*b*c, Sполн = 2(ab + ac + bc).
Пирамида — это многогранник, у которого одна грань (основание пирамиды) является произвольным многоугольником, а остальные грани (боковые грани) — треугольники с общей вершиной, называемой вершиной пирамиды. Перпендикуляр, опущенный из вершины пирамиды на ее основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть, соответственно, треугольной, четырехугольной, пятиугольной, шестиугольной и т. д. Треугольная пирамида является тетраэдром, четырехугольная — пятигранником и т. д. Пирамида называется правильной, если в основании лежит правильный многоугольник, а ее высота падает в центр основания. Все боковые ребра правильной пирамиды равны; все боковые грани — равнобедренные треугольники. Высота боковой грани называется апофемой правильной пирамиды.
Если провести сечение, параллельное основанию пирамиды, то тело, заключенное между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани называются основаниями; расстояние между ними — высотой. Усеченная пирамида называется правильной, если пирамида, из которой она была получена, — правильная. Все боковые грани правильной усеченной пирамиды — равные равнобочные трапеции.
Площадь боковой поверхности правильной пирамиды:
Объем усеченной пирамиды:
Площадь боковой поверхности правильной усеченной пирамиды:
Цилиндрическая поверхность образуется при движении прямой, сохраняющей свое направление и пересекающейся с заданной линией (кривой). Эта линия называется направляющей. Прямые, соответствующие различным положениям прямой при ее движении, называются образующими цилиндрической поверхности.
Цилиндром называется тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Части этих плоскостей называются основаниями цилиндра. Расстояние между основаниями — высота цилиндра. Цилиндр прямой, если его образующие перпендикулярны основанию; в противном случае цилиндр наклонный. Цилиндр называется круговым, если его основание — круг. Если цилиндр является одновременно и прямым, и круговым, то он называется круглым. Призма является частным случаем цилиндра.
Объем, площади боковой и полной поверхностей цилиндра:
Цилиндрические сечения боковой поверхности кругового цилиндра.
Сечения, параллельные основанию, — круги того же радиуса.
Сечения, параллельные образующим цилиндра, — пары параллельных прямых.
Сечения, которые не параллельны ни основанию, ни образующим, — эллипсы.
Коническая поверхность образуется при движении прямой, проходящей все время через неподвижную точку, и пересекающей за данную линию, называемую направляющей. Прямые, соответствующие различным положениям прямой при ее движении, называются образующими конической поверхности; точка — ее вершиной. Коническая поверхность состоит из двух частей: одна описывается лучом, другая — его продолжением.
Обычно в качестве конической поверхности рассматривают одну из её частей.
Конус — это тело, ограниченное одной из частей конической поверхности с замкнутой направляющей и пересекающей коническую поверхность плоскостью, не проходящей через вершину.
Часть этой плоскости, расположенной внутри конической поверхности, называется основанием конуса. Перпендикуляр, опущенный из вершины на основание, называется высотой конуса.
Пирамида является частным случаем конуса. Конус называется круговым, если его основанием является круг. Прямая, соединяющая вершину конуса с центром основания, называется осью конуса. Если высота кругового конуса совпадает с его осью, то такой конус называется круглым.
Объем, площади боковой и полной поверхностей конуса:
Объем и площадь боковой поверхности усеченного конуса:
Сечения кругового конуса, параллельные его основанию, — круги.
Сечение, пересекающее только одну часть кругового конуса и не параллельное ни одной его образующей, — эллипс.
Сечение, пересекающее только одну часть кругового конуса и параллельное одной из его образующих, — парабола.
Сечение, пересекающее обе части кругового конуса, в общем случае является гиперболой, состоящей из двух ветвей. В частности, если это сечение проходит через ось конуса, то получаем пару пересекающихся прямых (образующих конус).
Сферическая поверхность — это геометрическое место точек в пространстве, равноудаленных от одной точки, которая называется центром сферической поверхности.
Шар (сфера) — это тело, ограниченное сферической поверхностью. Можно получить шар, вращая полукруг (или круг) вокруг диаметра. Все плоские сечения шара — круги. Наибольший круг лежит в сечении, проходящем через центр шара, и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра, можно провести бесчисленное множество больших кругов.
Объем шара в полтора раза меньше объема описанного вокруг него цилиндра, а поверхность шара в полтора раза меньше полной поверхности того же цилиндра.
Часть шара (сферы), отсекаемая от него какой-либо плоскостью, называется шаровым (сферическим) сегментом. Круг называется основанием шарового сегмента. Отрезок перпендикуляра, проведенного из центра круга до пересечения со сферической поверхностью, называется высотой шарового сегмента. Часть сферы, заключенная между двумя параллельными плоскостями, пересекающими сферическую поверхность, называется шаровым слоем; кривая поверхность шарового слоя называется шаровым поясом (зоной). Расстояние между основаниями шарового пояса — его высота. Часть шара, ограниченная кривой поверхностью сферического сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара, называется шаровым сектором.