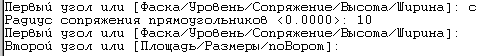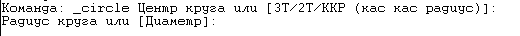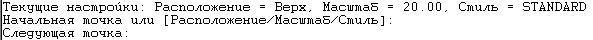что такое геометрическая модель

Лекция № 1. Геометрическое моделирование. Системы координат. Аффинные преобразования

Лекция 7

Геометрическое моделирование. Системы
координат. Аффинные преобразования

Основные понятия геометрического моделирования

Моделирование – один из основных методов познания, который заключается в выделении из сложного явления (объекта) некоторых частей и замещении их другими объектами, более понятными и удобными для описания, объяснения и разработки.

Модель – реальный физический объект или процесс, теоретическое построение, упорядоченный набор данных, которые отражают некоторые элементы или свойства изучаемого объекта или явления, существенные с точки зрения моделирования.

Математическая модель – модель объекта, процесса или явления, представляющая собой математические закономерности, с помощью которых описаны основные характеристики моделируемого объекта, процесса или явления.

Геометрическое моделирование – раздел математического моделирования – позволяет решать разнообразные задачи в двумерном, трехмерном и, в общем случае, в многомерном пространстве.

В настоящее время геометрическое моделирование успешно используется в управлении и других областях человеческой деятельности. Можно выделить две основные области применения геометрического моделирования: проектирование и научные исследования.

Геометрическое моделирование может использоваться при анализе числовых данных. В таких случаях исходным числовым данным ставится в соответствие некоторая геометрическая интерпретация, которая затем анализируется, а результаты анализа истолковываются в понятиях исходных данных.

Этапы геометрического моделирования:

● постановка геометрической задачи, соответствующая исходной прикладной задаче или ее части;

● разработка геометрического алгоритма решения поставленной задачи;

● реализация алгоритма при помощи инструментальных средств;

● анализ и интерпретация полученных результатов.

Методы геометрического моделирования:

● графический, с использованием средств машинной графики;

Графоаналитические методы основываются на разделах вычислительной геометрии, таких как теория R-функций, теория поверхностей Кунса, теория кривых Безье, теория сплайнов и др.

Системы координат

Система координат (СК) – совокупность базисных (линейно независимых) векторов и единиц измерения расстояния вдоль этих векторов (e1, e2, …, en).

Если базисные вектора нормированы (единичной длины) и взаимно ортогональны, то такая СК называется декартовой (ДСК).

Мировая система координат (МСК) – xyz – содержит точку отсчета (начало координат) и линейно независимый базис, благодаря которым становится возможным цифровое описание геометрических свойств любого графического объекта в абсолютных единицах.

Экранная система координат (ЭСК) – xэyэzэ. В ней задается положение проекций геометрических объектов на экране дисплея. Проекция точки в ЭСК имеет координату zэ = 0. Тем не менее, не следует отбрасывать эту координату, поскольку МСК и ЭСК часто выбираются совпадающими, а, вектор проекции [xэ, yэ, 0] может участвовать в преобразованиях, где нужны не две, а три координаты.

Объектная система координат (ОСК) – xоyоzо – связана с конкретным объектом и совершает с ним все движения в СКС или МСК.

Правая ДСК – оси ориентированы так, что вращение ортов происходит в положительном направлении (против часовой стрелки с точки зрения наблюдателя, находящегося на конце третьего свободного орта):

Левая ДСК – оси ориентированы так, что вращение ортов происходит в отрицательном направлении.

В двумерном пространстве (R2) наиболее распространены декартова СК (x, y) и полярная СК (r, φ) (r – радиус-вектор точки, φ – угол поворота).

Соотношение между ДСК и ПСК:

В трехмерном пространстве (R3):

● цилиндрическая СК (ρ, y, φ);

Соотношение между декартовой СК и цилиндрической СК:

Соотношение между декартовой СК и сферической СК:

Соотношение между цилиндрической СК и сферической СК:

Аффинные преобразования

Аффинным называется преобразование, обладающее следующими свойствами:

● любое аффинное преобразование может быть представлено как последовательность операций из числа простейших: сдвиг, растяжение/сжатие, поворот;

● сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.

Аффинные преобразования координат на плоскости:

(x, y) – двумерная система координат,

(X, Y) – координаты старой СК в новой системе координат.

Общий вид аффинного преобразования:

Обратное преобразование также является аффинным:

Простейшие аффинные преобразования системы координат.

1.

Параллельный сдвиг координат:

Обратное преобразование:

2. Растяжение/сжатие осей:

Обратное преобразование

:

3. Поворот системы координат (x,y) на угол α:

Обратное преобразование – поворот системы (X,Y) на угол (-α):

Аффинные преобразования объектов на плоскости.

x, y – старые координаты точки, X, Y – новые координаты точки.

1.

Сдвиг:

Обратное преобразование:

2.

Масштабирование объекта:

3. Поворот вокруг центра координат:

Лекция 8

Геометрические модели плоских объектов

Основные понятия

Положение точки в пространстве Rn (n-мерном пространстве) задается радиус-вектором p=[p1, p2, …, pn], имеющим n координат p1, p2, …, pn и разложение по n линейно-независимым базисным векторам e1, e2, …, en :

.

Таким образом положение точки на плоскости определяется радиус-вектором точки p=[px, py]= pxex +pyey или p=[r, φ] в полярной системе координат.

Расстояние между двумя точками p1 и p2 равно:

Линия на плоскости может быть задана с помощью уравнения в неявной форме:

или в параметрической форме:

В любой регулярной (гладкой и некратной) точке на линии p0=[x0, y0]=p(t0) возможна линеаризация кривой, т. е. проведение к ней касательной прямой, уравнения которой имеют вид

Вектор нормали N=[Nx, Ny] ортогонален линии и направлен в ту сторону, где f(p)> 0.

Направляющий вектор линии V=[Vx, Vy] начинается в точке p0 и направлен по касательной к p(t) в сторону увеличения t.

Векторы N и V ортогональны, т. е. N ◦ V = 0 или NxVx + NyVy = 0.

Связь вектора нормали и направляющего вектора:

Способы описания (модели) прямой линии

Неявное уравнение прямой задается тремя коэффициентами A, B и D, составляющими вектор F=[A, B, D]:

Хотя бы одно из чисел A или B должно быть ненулевым.

Если оба коэффициента ненулевые (A≠0 и B≠0), то прямая проходит наклонно к осям координат и пересекается с ними в точках (-D/A, 0) и (0, —D/B).

Прямая проходит через начало координат: f(0,0)=0 при D=0.

Благодаря свойству прямой разделять плоскость на две полуплоскости с противоположными знаками, неявное уравнение позволяет определять положение точки (точек) на плоскости относительно прямой:

1) точка q лежит на прямой, если f(q)=0;

2) точки a и b лежат по одну сторону от прямой, если f(a)∙f(b)>0;

3) точки a и b лежат по разные стороны от прямой, если f(a)∙f(b) 0 точка a лежит в том же полупространстве, куда направлена нормаль, а угол Ð(a—p0, N) острый;

● при f(b) 0 точка a лежит справа от точки p0, так что угол Ð(a—p0, V) положительный;

Источник

геометрическая модель

Смотреть что такое «геометрическая модель» в других словарях:

геометрическая модель — Нрк макет Модель, находящаяся в отношении геометрического подобия к моделируемому объекту. [Сборник рекомендуемых терминов. Выпуск 88. Основы теории подобия и моделирования. Академия наук СССР. Комитет научно технической терминологии. 1973 г.]… … Справочник технического переводчика

Геометрическая модель местности — (фототопография) совокупность точек пересечения соответственных проектирующих лучей, полученная по стереопаре ориентированных топографических фотоснимков. Источник: ГОСТ Р 52369 2005. Фототопография. Термины и определения (утв. Приказом… … Официальная терминология

геометрическая модель местности (фототопография) — Совокупность точек пересечения соответственных проектирующих лучей, полученная по стереопаре ориентированных топографических фотоснимков. [ГОСТ Р 52369 2005] Тематики фототопография Обобщающие термины виды топографических фотоснимков и их… … Справочник технического переводчика

геометрическая модель местности — 37 геометрическая модель местности (фототопография): Совокупность точек пересечения соответственных проектирующих лучей, полученная по стереопаре ориентированных топографических фотоснимков. Источник: ГОСТ Р 52369 2005: Фототопография. Термины и… … Словарь-справочник терминов нормативно-технической документации

электронная геометрическая модель (геометрическая модель) — электронная геометрическая модель (геометрическая модель): Электронная модель изделия, описывающая геометрическую форму, размеры и иные свойства изделия, зависящие от его формы и размеров. [ГОСТ 2.052 2006, статья 3.1.2] Источник … Словарь-справочник терминов нормативно-технической документации

Электронная геометрическая модель изделия — Электронная геометрическая модель (геометрическая модель): электронная модель изделия, описывающая геометрическую форму, размеры и иные свойства изделия, зависящие от его формы и размеров. Источник: ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ.… … Официальная терминология

МОДЕЛЬ — абстрактное или вещественное отображение объектов или процессов, адекватное исследуемым объектам (процессам) в отношении некоторых заданных критериев. Напр., математическая модель слоенакопления (абстрактная модель процесса), блок диаграмма… … Геологическая энциклопедия

Модель изделия каркасная — Каркасная модель: трехмерная электронная геометрическая модель, представленная пространственной композицией точек, отрезков и кривых, определяющих в пространстве форму изделия. Источник: ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ. ЭЛЕКТРОННАЯ… … Официальная терминология

Модель изделия поверхностная — Поверхностная модель: трехмерная электронная геометрическая модель, представленная множеством ограниченных поверхностей, определяющих в пространстве форму изделия. Источник: ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ. ЭЛЕКТРОННАЯ МОДЕЛЬ… … Официальная терминология

Модель изделия твердотельная — Твердотельная модель: трехмерная электронная геометрическая модель, представляющая форму изделия как результат композиции заданного множества геометрических элементов с применением операций булевой алгебры к этим геометрическим элементам. … … Официальная терминология

Источник

Что такое геометрическая модель

электронный учебно-методический комплекс

Тема 2. Геометрическое моделирование

История геометрического моделирования начинается с первых работ по машинной графике о графическом представлении и основы для алгоритмов удаления невидимых частей. Появляются первые системы для моделирования сплошных тел. В 70-х годах начинается промышленное применение моделирования сплошных тел, а в моделях учитываться функциональные особенности, прежде всего благодаря совершенствованию аппаратуры (мультипликация, цвет и т.д.).

Геометрическая модель изделия является машинным представлением его формы и размеров. Двумерная модель изделия, которая может включать реляционную информацию, отличается от модели для визуализации, которая содержит векторные данные. Не следует думать, например, что используемая модель не относится к объемным моделям типа сплошного тела (в ней отсутствуют сведения о материале) лишь потому, что система может выводить на экран только линейные рисунки. Модель можно формировать различными методами, она может создаваться как результат вычислений, а отнюдь не на экране.

Двумерные модели, которые позволяют формировать и изменять чертежи, были первыми моделями, нашедшими применение. Применяются они в промышленности и до сих пор, т.к. существенно дешевле в отношении алгоритмов и программного обеспечения.

Однако двумерное представление часто не совсем удобно для достаточно сложных изделий. Трехмерная модель служит для того, чтобы создать виртуальное представление изделия во всех трех измерениях.

В работах, проведенных в этой области, и в соответствующих комплексах программного обеспечения выделяются три основных типа трехмерных моделей:

каркасные («проволочные») модели;

модели сплошных тел («объемные»).

Исторически первыми появились каркасные модели. В них хранятся только координаты (x, y, z,) вершин и соединяющие их ребра.

Поверхностная модель позволяет описывать иногда достаточно сложные поверхности. Возможны различные виды задания поверхностей – плоскости, поверхности вращения, линейчатые поверхности. Используются различные математические модели аппроксимации поверхностей (методы Кунса, Безье, В-сплайны). Они позволяют изменять характер поверхности с помощью параметров, смысл которых доступен пользователю, не имеющему специальной подготовки.

Объемная модель позволяет представить сложные изделия с обеспечением логической связанности информации, в частности, благодаря введению понятия о материале.

— любая модель, которую можно сконструировать, не должна противоречить реальному объекту (правильность модели);

— допустимо конструирование модели объекта целиком;

возможно вычисление ряда геометрических величин, например, объемов и т. д.;

— предусмотрено использование различных функций (ЧПУ, разработка серии изделий, расчет конструкций).

Для удовлетворения этих требований необходимо, чтобы модель обладала определенным набором математических свойств, например:

1. Однородность: тело должно быть заполнено внутри;

2. Конечность: тело должно занимать конечную часть пространства;

3. Жесткость: сплошное тело должно сохранять свою форму независимо от положения и ориентации.

Кроме того, программная система должна удовлетворять следующим требованиям:

— согласованность операций: любая операция, выполняемая над телами, должна приводить к образованию сплошных тел;

— возможность описания: каждое тело должно быть представимо в машинном виде;

— непротиворечивость информации: точка пространства может принадлежать не более чем одному телу.

Под техническим черчением понимается использование методов, которые традиционно применяются чертежниками, но с использованием средств информатики (дисплеи, средства диалога и т. д.). Соответствующие программы для ЭВМ дают возможность пользователю формировать и изменять в интерактивном режиме чертежи.

Данные, которые хранятся в модели, значительно различаются в зависимости от требуемого качества моделирования. Рассмотрим, какого рода данные наиболее характерны для четырех основных типов моделей.

1. Двумерная модель. В простых моделях удовлетворяются тем, что работают с элементами, которые близки к уровню визуализации. В сложных моделях элементы ассоциируются функционально, например, размерные линии соотносятся с объектами или же запоминаются способы соединения элементов.

2. Каркасная модель. В ней хранится информация двух типов:

топологическая (ребра, определяемые вершинами) и геометрическая (координаты вершин).

3. Поверхностная модель. В моделях этого типа хранится только описание поверхностей. Однако эти поверхности могут сильно различаться. И разработчики моделей для работы с поверхностями используют математические методы компактного представления, обеспечивающие возможность интерактивного режима и сложных расчетов.

4. Объемная модель. В такой модели хранится информация, позволяющая отличать материал от пустоты, при этом пустота может

рассматриваться как особый вид материала.

В настоящее время используют два метода:

— объект представлен в модели охватывающей его «оболочкой». Тогда, как и в каркасной модели, сохранятся информация геометрического и топологического типа, однако она более полная (грани заданы и ориентированы таким образом, что известны их наружная и внутренняя стороны)

— объект представлен в модели операциями построения, использованными для его задания.

В заключение отметим тот факт, что в рамках одного конкретного применения обычно используется не одна модель, а несколько. Во многих системах сосуществуют геометрическая модель (в ряде случаев весьма высокого уровня – объемная, поверхностная) и модель для визуализации, которая дает возможность работать с информацией, близкой к чисто графической (при графическом выводе, интерактивной работе и т. д.).

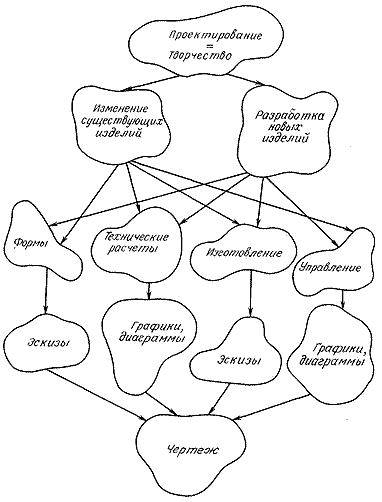
В процессе традиционного проектирования и изготовления передача информации осуществляется с помощью тестов и чертежей. Таким образом, как для новых, так и для стандартизированных изделий большинство документов представлено в графической форме: чертежи, графики, диаграммы и т. д., рисунок 1.

На предприятиях и конструкторских бюро основными видами проектной деятельности от общей трудоемкости являются: черчение – 70%; организация архивов и их ведение – 15%; собственно проектирование – 15%; которое в свою очередь подразделяется на копирование – 70%; модификацию вариантов – 20%; исправление ошибок – 9%; разработку – 1%.

Интерактивное создание детали и изготовление графических документов в САПР дает более качественное изображение, как в

визуальном отображении, так и в твердой копии, чем работа моделирующей программы, которая выдает несколько числовых значений. Для этого используется интерактивное программное обеспечение:

— центром всего комплекса является программа, которая должна выполнять расчеты, непосредственно связанные с данной областью;

— исходная информация подается с помощью операций ввода, результаты выдаются с помощью операций вывода;

— интерактивный режим (или диалог) ведет оператор, который анализирует результаты, может менять работу программы, вводя в нее новую исходную информацию.

Рисунок 1. Виды деятельности в процессе проектирования САПР

Двумерная геометрическая модель оперирует данными следующих типов:

— геометрическими (отрезок, соединяющий две точки, контур, определенный своими базовыми объектами, направления обхода и пересечения и т. д.);

— структурными (комплекс состоит из базовых элементов), структурирование, ориентированное на понятия сборки, часто выполняется в виде дерева;

— оформительскими (размерные линии, тексты, штриховка, различные условные обозначения), например, оформление чертежа должно выполняться на двумерной модели, которая может содержать много полезных сведений, в частности о связях между размерами и соответствующими элементами. О методах построения, реализуемых достаточно просто и имеющих много достоинств, использование библиотек символов, геометрические преобразования;

— графическими (в большинстве случаев очень удобна для визуализации), вот почему часто графические данные хранятся в двумерной модели. К ним можно отнести тип линии (штриховая, сплошная, штрихпунктирная и т.д.);

— топологическими (отрезок, соединяющий две точки, контур, опреде­ленный своими базовыми объектами, направления обхода и пересечения и т.д.);

— графическими (двумерная модель в большинстве случаев очень удоб­на для визуализации). Вот почему часто графические данные хранятся в двумерной модели. К ним можно отнести, в частности, тип линии (штриховая, сплошная, штрихпунктирная и т. д.) для базовых элементов или же сведения более высокого уровня, например, о визуализации или выборе видов.

Элементы, с которыми работают в двумерной модели, могут быть весьма разнообразными в различных прикладных задачах. Если в такой задаче требуется использовать символы, соединенные между собой с той или иной степенью сложности, то базовыми элементами, хранящимися в модели, будут символы и связи. В других случаях, например при моделировании машиностроительных чертежей, базовыми элементами будут отрезок прямой и окружность.

Ниже изложен опыт двумерного моделирования в машиностроении с использованием программного обеспечения для технического черчения, которые позволяют оценить различия возможных моделей.

К базовым объектам, с которыми работает программное обеспечение для технического черчения, относятся главным образом точка, отрезок прямой, прямая, дуга окружности, окружность, лекальная кривая, текст и контур. При этом могут быть использованы, например, следующие определения:

Пользователь не может непосредственно манипулировать элементами, предназначенными для оформления чертежа, в частности размерами и штриховкой.

В тех случаях, когда размер соотносят с объектами, он зависит от объектов, точки и числового значения:

Объекты можно объединять в комплексы и затем вызывать как ком­плекс, так и составляющие его объекты. В любой момент пользователь может работать в диалоговом режиме с одним или несколькими объек­тами одновременно, а также с одним или несколькими комплексами или с полным чертежом.

Основными возможными типами построений являются построение при ограничениях и построение с использованием геометрических преобразований.

Построение при ограничениях применяется к объекту. Ограничение определяется следующим образом:

Реализуемая функция задается путем выбора объекта, подлежащего построению, типа налагаемых на него ограничений, а также параметров (других объектов, связанных с этим ограничением, и (или) значений). Реализацию диалога мы рассмотрим более подробно в лекции 5. Объекты, связанные с выбранным типом ограничения, указывает пользователь. Затем программное обеспечение определяет типы этих объектов (точка, дуга и т.д.) и их параметры. Наличие или отсутствие параметров, за данных значением, позволяет полностью определить действие, которое должно быть выполнено программами.

Пользуясь основными типами ограничений, можно построить объект, который:

Кроме того, некоторые очень распространенные построения особенно удобно применять в диалоговом режиме, например сопряжение и нахождение биссектрисы.

1. Общее решение построения можно получить в два этапа:

1) составляя (на основе типов ограничений, элементов и параметров) систему алгебраических уравнений и

2) решая эту систему (значения, характеризующие искомый элемент, принадлежат множеству решений системы уравнений).

Очевидным достоинством этого способа является его общность,

Поскольку, для добавления нового ограничения достаточно написать соответствующие уравнения.

Его недостатками являются следующие:

Построения для отдельных элементов и ограничений.

В этом случае требуется написать подпрограмму для триады, в которую входят задаваемый элемент, тип ограничения, прочие элементы, затрагиваемые ограничением.

Преимущество такого способа состоит в том, что не приходится прибегать к очень сложным методам вычислений. Поиск решения полностью управляем.

Кроме того, в этом случае можно организовать библиотеку подпрограмм, пригодных в различных применениях.

Основной недостаток состоит в том, что для добавления нового ограничения или нового типа элемента требуется написать одну или несколько новых подпрограмм.

Этот способ часто предпочитают, чтобы избежать использования итерационных методов, которые в определенных случаях могут оказаться неэффективными, и пополнять библиотеку геометрических построений, которая служит основой для многочисленных применений (параметризованные формы и т.д.).

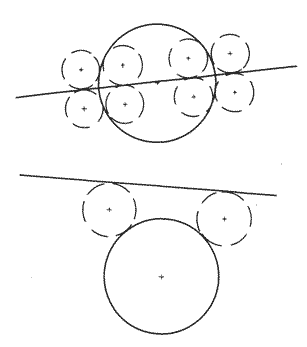
Рассмотрим пример использования этого решения. Требуется найти окружность, касательную к заданным прямой и окружности, если известны радиус искомой окружности и примерное положение ее центра. Задание примерного положения часто используется для выбора одного объекта среди множества объектов, удовлетворяющих ограничениям.

Для упрощения изложения выбрано простое ограничение.

Известно уравнение прямой:

Окружность задается своим центром Х1,У1 и радиусом R1.

Центр окружности находится на прямой, параллельной прямой, заданной уравнением (1). Составим уравнения для прямых, параллельных, заданной уравнением (1), подставляя значения Хс и Ус вместо х и у, мы можем непосредственно определить, к какой из двух прямых ближе точка.

Рисунок 2 – Окружности, касательные к заданным окружности прямой

Геометрическим местом центров окружностей, касательных к заданной окружности (Х1, У1, R1), является одна из окружностей с центром и радиусом соответственно (Х1, У1, R1 + R).

Центр искомой окружности, таким образом, располагается на пересечении прямой и одной из этих окружностей.

Рисунок 3 – Пример библиотеки программ для геометрических вычислений

Все точки пересечения помещаются в таблицу. Обращение к функции PLUHRE позволяет определить, какая из этих точек находится ближе к примерной точке Хс, Ус.

Комплекс подпрограмм позволяет строить матрицы, определяющие различные геометрические преобразования, и выполнять операции путем умножения матриц. Преобразования выполняются следующим образом:

▪ находится матрица, определяющая глобальное преобразование, путем обращения к подпрограммам задания преобразований и умножения
матриц;

▪ выполняется умножение матриц на векторы для всех характерных точек объекта, подвергаемого преобразованию. Для углов производят расчет, позволяющий перейти к точкам, а затем также применяют умножение матрицы на вектор.

Объединение базовых элементов может либо выполняться только на уровне структурирования, либо основываться на топологических и геометрических соотношениях, либо же относиться к элементам оформления.

В сущности речь идет о средствах, которые позволяют указать некоторое число элементов, принадлежащих одному комплексу. Тогда появляется возможность работать с комплексами в целом, что несомненно удобно как при визуализации, так и при функциональном структурировании.

При функциональном структурировании из базовых элементов формируются детали (в некоторых системах они называются группами). Число уровней функционального структурирования может быть довольно большим, а структура часто имеет вид дерева. Назначение этих уровней состоит в том, чтобы обеспечить сборку узлов различной степени сложности. Поэтому на уровне модели хранится дополнительная информация, например о точках ШАРНИР и РЫЧАГ, что позволяет облегчить размещение этих элементов (путем переноса и поворота). При реализации прикладных задач САПР очень важно, чтобы модель могла воспринимать информацию негеометрического типа, например о видах соединений («ось-ось» и т.д.).

Рассмотрим один из способов построения контуров. Контур представляет собой упорядоченный список объектов и может быть разомкнутым или замкнутым. Для замкнутого контура определены внутренняя и наружная области, благодаря этому его можно заштриховать.

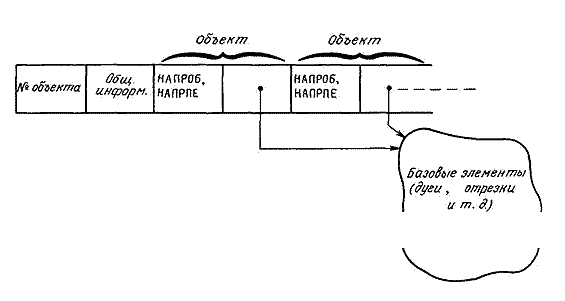
Рисунок 4 – Структура контура

Характер моделирования контура зависит от используемых при этом базовых элементов. В системе GRI2D контур включает следующую информацию:

а) число элементов, образующих контур;

б) общую информацию о контуре (замкнутый разомкнутый, тип линии и т. д.);

в) объекты, образующие контур с указанием:

направления обхода объекта:

объекты находятся в порядке, определенном их положением в списке, а каждый объект обходится в направлении, определенном параметром НАПРОБ (направление обхода, принятое в базовом элементе, или же противоположное направление);

признака выбора пересечения:

если из двух смежных объектов хотя
бы один представляет собой окружность, для выбора точки пересечения
иногда недостаточно параметра направления обхода. Поэтому добавляется параметр НАПРПЕ (направление пересечения), который включает все возможные случаи пересечения.

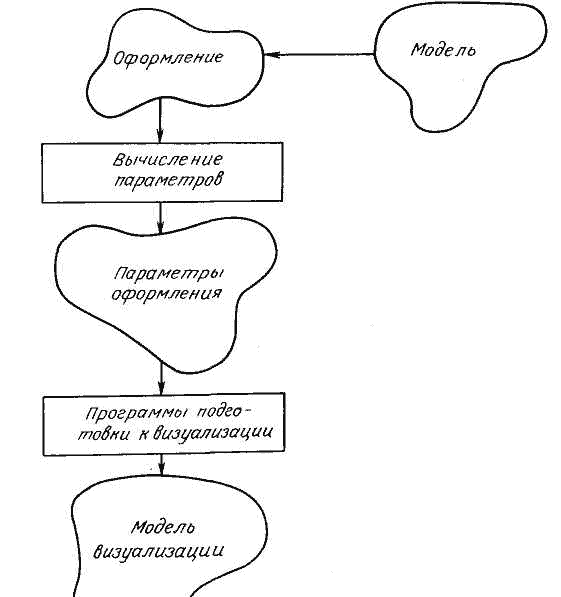
При моделировании контура в такой функциональной форме необходимо иметь алгоритмы для подготовки к визуализации. В данном случае контур можно представить двумя способами:

В состав оформления входят размеры, штриховка и надписи, эти данные предназначены для использования в двумерной модели, их рассматривают как особый вид графических обозначений. При оформлении необходимо строго соблюдать стандарты.

Поэтому с целью подготовки к визуализации приходится разрабаты­вать многочисленные программы для самых разнообразных случаев с учетом стандартов. При этом приходится делать выбор между чисто графическим подходом и привязкой оформления к модели; такой выбор, осуществляемый с учетом принятой методологии конкретной разработки, можно рассматривать как выбор модели с большим или меньшим уровнем сложности. Так, например, если привязка соответствует рисунок 6, то для простановки размера требуется следующее описание:

СОТ 2 PTS:F (POINT1, POINT2, POINT DE TRAVAIL)

Оформление рассматриваемое как чисто графический элемент, является функцией конечного числа параметров, которые используются программой полготовки к визуализации.

PAFCOT (XI, Yl, Х2, Y2, DIR, XFLC, YFLC, XTX, YTX, ANG, LGTX, CHAIN)

Рисунок 5 – «Полуфункциональное» оформление

Такая общая схема обеспечивает возможность сосуществования элементов оформления, привязанных к модели, базовым объектам, штриховки – к контурам, текста – к основным частям чертежа и оформления графического типа.

В заключение, необходимо отметить, что библиотека подготовки к визуализации должна содержать большое число программ из-за многочисленности символов, которые могут быть предусмотрены в стандарте.

Панель «Рисование» в программе AutoCAD 2007 предназначена для выполнения различных графических примитивов (линий, окружностей, дуг и прочих элементов), нанесения штриховки, а также выполнения текстовых надписей. Плавающая панель «Рисование» представлена на рисунке 14.

Рисунок 14 – Панель «Рисование»

Рассмотрим способы построения простейшего графического примитива – отрезка. Для проведения линии на чертеже нужно выбрать из панели «Рисование» команду «отрезок» . Затем, потребуется указать координаты начальной и конечной точки. Данные указания можно выполнить несколькими способами:

1) при помощи мыши (щелкнув левой кнопкой мыши в какой-либо точке чертежа);

2) задание координат точек отрезка при помощи клавиатуры. При этом первое число подразумевает координату по оси Х, второе – по оси Y (координаты вводятся через запятую. В этом случае координаты точки также отсчитываются относительно начала координат.

3) использование относительных координат (относительно последней точки построений). При этом в командной строке вводится специальный символ @, а затем указываются смещения по осям Х и Y. Задание конечной точки отрезка возможно несколькими способами.

4) С помощью метода «направление-расстояние». При этом методе указания второй точки осуществляется путем перемещения курсора в нужном направлении (включить режим ОРТО) и ввода значения расстояния (длины отрезка) с клавиатуры. Такой способ задания конечной точки используется только в том случае, если отрезок параллелен какой-либо оси

5) С помощью метода «расстояние-угол». При этом методе указания второй точки осуществляется путем перемещения курсора в нужном направлении (выключить режим ОРТО) и ввода значения длины отрезка и угла наклона с клавиатуры. Этот метод применяется для построения отрезка под углом к осям координат.

Команда «Отрезок» имеет опции [Замкнуть, Отменить], которые заключены в квадратные скобки. Чтобы отменить построение предыдущего сегмента, нужно ввести букву «О» в командной строке, ввод буквы «З» приведет к замыканию линии, то есть соединению последней точки построения с первой.

Позволяет строить линии бесконечной длины. Положение прямой определяется двумя точками, поэтому для ее построения необходимо указать точку на чертеже левой кнопкой мыши или ввести координаты с клавиатуры, затем указать вторую точку.

Команда предназначена для построения правильных многоугольников. При выполнении команды указывается:

— число сторон многоугольника. ENTER;

— затем точка центра;

— опция размещения (вписанный в окружность или описанный вокруг окружности). ENTER.

— указывается радиус окружности. ENTER.

Команда предназначена для построения прямоугольников. Для построения произвольного прямоугольника достаточно указать координаты первого угла (мышью или с клавиатуры), а затем, задать размеры по осям X и Y.

Команда имеет пять опций:

Опция «Фаска» позволяет строить прямоугольники со срезанными углами. При этом, нужно указать параметры фаски. Диалог будет выглядеть следующим образом:

Опция «Уровень» определяет уровень прямоугольника относительно плоскости нулевого уровня (используется в трехмерных моделях).

Опция «Сопряжение» позволяет строить прямоугольники со скругленными углами. Пример диалога командной строки:

Опция «Высота» задает высоту прямоугольника над плоскостью нулевого уровня.

Опция «Ширина» определяет ширину линии, которой вычерчиваются прямоугольники. Эта опция аналогична опции «Ширина» в команде полилиния.

После указания первого угла прямоугольника необходимо указать второй угол. Для этого можно использовать следующие опции, позволяющие построить прямоугольник по заданным размерам или с заданной площадью.

Вычерчивание дуги. Кнопка на плавающей панели инструментов предусматривает построение дуги по трем точкам. Координаты точек указываются мышью или вводятся с клавиатуры.

Если войти в команду «Дуга» ниспадающей панели «Рисование», то можно выбрать различные варианты построения дуги.

Построение окружности. Кнопка на плавающей панели инструментов выполняет построение окружности с указанием точки центра и радиуса. При этом точка центра указывается либо мышью на экране, либо вводом координат с клавиатуры. Радиус можно также указать мышью или ввести значение радиуса в командной строке. Если выбрать опцию «Диаметр», то есть ввести букву «Д», то выполнится построение окружности по указанному диаметру.

6.7. Команда «Облако»

Построение замкнутого объекта, состоящего из дуг определенного радиуса. Максимальный радиус дуги можно определить в опциях команды, набрав букву «Д». Опция «Стиль» позволяет переключиться на каллиграфический стиль, то есть дуги, составляющие объект, будут иметь различную ширину в начальной точке и в конечной. Опция «Объект» выполняет построение облака вокруг какого-либо объекта.

Построение волнистых линий. Эта команда позволяет строить сложные математические кривые, огибающие некоторые опорные точки и аппроксимирующие участки плоских кривых (эллипса, окружности, параболы, гиперболы). Мы будем ее использовать с чисто практической точки зрения – для построения волнистой линии, которой нет в стандартных типах линий. При построении сплайна необходимо указать несколько точек, через которые будет проходить кривая, нажать ENTER или правую кнопку мыши, затем в командной строке появится запрос «касательная в начальной точке». Направление касательной можно указать мышью, или ввести значение угла касательной с клавиатуры. Так же указывается направление касательной в конечной точке. Сплайн построен.

Построение эллипсов. При выполнении команды необходимо указать конечные точки оси эллипса, затем указать мышью или ввести с клавиатуры длину другой полуоси. Команда имеет две опции [Дуга/ Центр]. Первая позволяет построить эллиптическую дугу. При этом сначала задаются все параметры для построения эллипса, затем, указывается значение начального и конечного угла эллиптической дуги.

При выборе опции «Центр» построение эллипса осуществляется указанием его центральной точки и длин полуосей.

Использование второй команды «Эллиптическая дуга» дублирует построение эллиптической дуги при помощи опции «Дуга» команды «Эллипс».

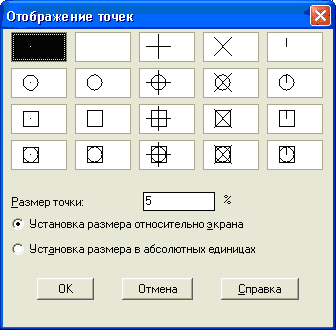
Построение точки по указанным координатам. Положение точки можно задать также щелчком мыши. При этом на экране появится точка. Отображение точек в AutoCAD может быть различным. В падающем меню «Формат» находится команда «Отображение точек», которой вызывается одноименное диалоговое окно (рисунок 17), позволяющее установить стиль изображения точек, а также их размер в процентах относительно экрана или в абсолютных единицах.

Рисунок 17 – Диалоговое окно «Отображение точек»

Команда «Область» инициализирует все внутренние точки какого-либо замкнутого контура в единый объект. В результате получается трехмерный объект с нулевой толщиной. С областями можно выполнять логические операции: сложение, вычитание и пересечение.

Полилиния представляет собой объект, в котором комбинируются линейные сегменты и дуги. Интересным и полезным свойством, присущим полилиниям, является ширина, которая позволяет чертить линии и дуги разной толщины. Объект, вычерченный как полилиния, воспринимается как единый объект. В этом состоит основное ее преимущество перед контуром, созданным при помощи команды «отрезок». При вызове команды «Полилиния» в командной строке появляется запрос «Начальная точка». Начальную точку можно указать мышью или введением координат с клавиатуры. Затем появляется строка со списком опций.

При выборе опции «Дуга» в командной строке появится список опций для построения дуги:

Мультилинией называется линия, состоящая из нескольких параллельных прямых. Команда «Мультилиния» вызывается из падающего меню «Черчение». В общем случае команда выполняется также как команда «отрезок». При этом в командной строке содержится информация о текущих настройках мультилинии, а также опции команды.

Опция «Расположение» позволяет установить привязку начальной точки мультилинии к ее верхнему или нижнему краю, либо к середине.

Масштаб определяет расстояние между двумя крайними параллельными линиями, составляющими мультилинию.

Стиль «STANDARD» загружен в AutoCAD по умолчанию и представляет собой две параллельные прямые. Пользователь может создать собственный стиль, который определяется количеством элементов мультилинии, их цветом, расположением и прочими параметрами.

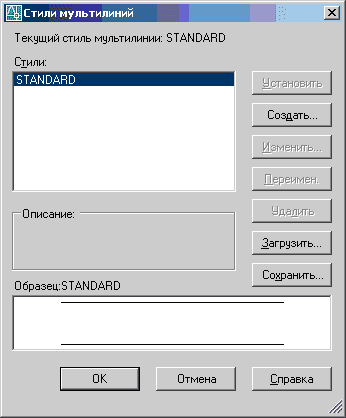
Рисунок 42 – Диалоговое окно «Стили мультилиний»

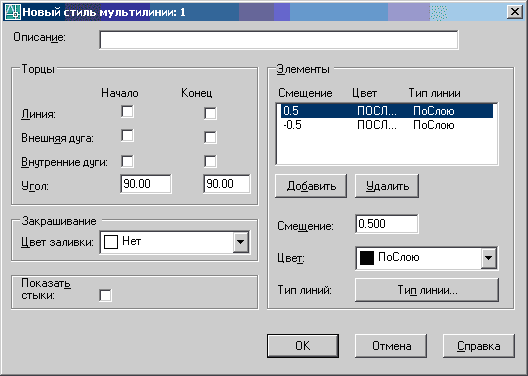
При нажатии кнопки «Создать» появляется диалоговое окно «Создание нового стиля», в котором вводится имя стиля мультилинии – любые буквы или цифры. Затем в диалоговом окне «Новый стиль мультилинии» (рисунок 43) необходимо определить параметры мультилинии, то есть ввести ее описание (при необходимости), форму торцов (отрезок или дуга), добавить элементы, указать их тип линии, цвет, смещение от середины, можно выполнить заливку мультилинии.

После определения всех параметров нажмите «ОК». Имя нового стиля появится в диалоговом окне «Стили мультилиний». В этом окне можно переключаться с одного стиля на другой нажатием кнопки «Установить». В этом же окне возможно редактирование стиля при помощи кнопок «Изменить», «Переименовать» и «Удалить».

Рисунок 43 – Диалоговое окно «Новый стиль мультилинии»

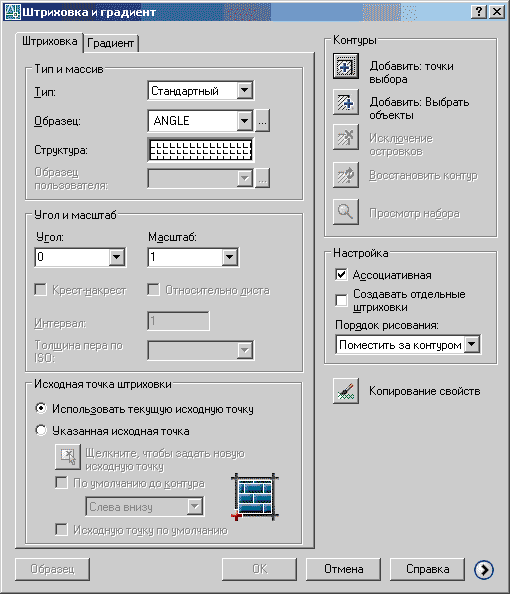
Осуществляет выполнение штриховки. При вызове этой команды появляется диалоговое окно «Штриховка и градиент» (рисунок 18), в котором можно выбрать тип штриховки, нажав кнопку «Образец», задать угол штриховки, а также расстояние между штрихами (кнопка «Масштаб»). Чем больше параметр масштаба, тем реже расположены линии штриховки.

Рисунок 18 – Диалоговое окно «Штриховка и градиент»

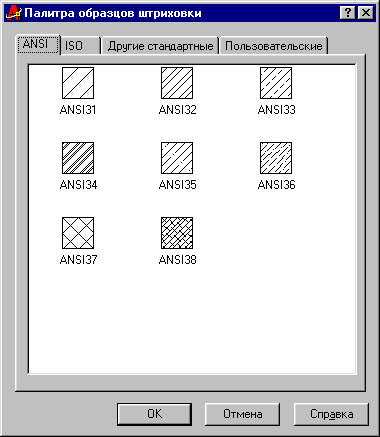
Если щелкнуть мышью в окне «Структура», то появится диалоговое окно «Палитра образцов штриховки» (рисунок 19), в котором можно выбрать образец штриховки. Обычно при выполнении разрезов машиностроительных деталей выполняется штриховка сплошной тонкой линией под углом 45º. Для выбора этого образца нажмите закладку ANSI – это стандартные образцы штриховки, и выберите штриховку ANSI31. Этот тип штриховки уже предусматривает наклон линий штриховки под углом 45°, поэтому параметр угла остается равным 0.

Далее необходимо определить область, которую мы хотим заштриховать. Это можно сделать двумя способами: указанием точки внутри контура (кнопка «Указание точек») или выбором объекта, который необходимо заштриховать (кнопка «Выбор объектов»). При нажатии кнопки «Указание точек» в командной строке появится запрос: «укажите внутреннюю точку». Выберите точку внутри замкнутой области, которая определяет создаваемый контур. Далее будет предложено выбрать другую внутреннюю точку, система может определять при этом множество контуров. После того как контур определен, нажмите правую кнопку мыши или «Enter». В появившемся контекстном меню выберите команду «Просмотр». Если штриховка выбранного объекта выполнена правильно, то нажмите «Enter», если нет – то «Esс». При этом возвращается диалоговое окно «Штриховка по контуру». Можно изменить параметры штриховки, затем нажать «ОК».

Рисунок 19 – Диалоговое окно «Палитра образцов штриховки»

8.2. Команда «Градиент»

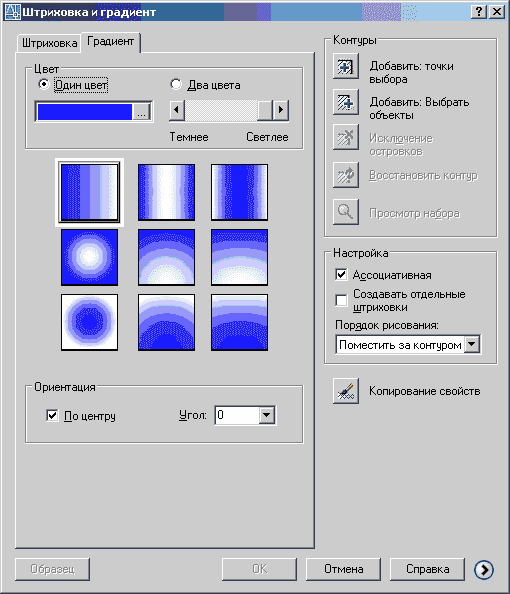
Производит заливку замкнутого контура одним или двумя цветами. При выполнении команды появляется диалоговое окно «Штриховка и градиент» (рисунок 20), в котором выбирается цвет и тип заливки, указывается объект или внутренняя точка закрашиваемого объекта.

Рисунок 20 – Диалоговое окно «Градиент»

Кнопка диалогового окна «Копирование свойств» позволяет скопировать штриховку или заливку на какой-нибудь другой объект чертежа.

В поле окна «Настройка» устанавливаются флажки «Ассоциативная» или «Создать отдельные штриховки», посредством которых можно установить связь штриховки с контуром. Ассоциативная штриховка или заливка подразумевает создание штриховки, связанной с контуром. При изменении формы контура в соответствии с ним изменится и штриховка. При создании отдельных штриховок этого не произойдет, то есть штриховка сохранит свою первоначальную форму.

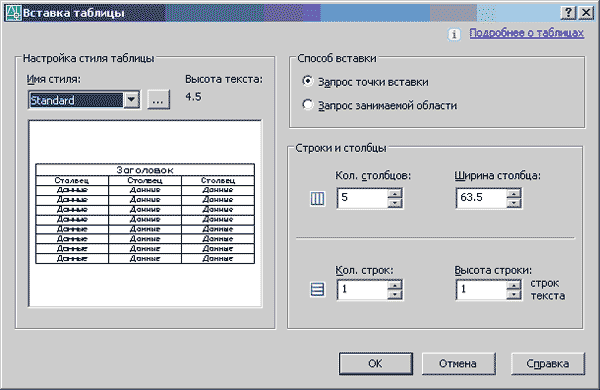
Создание таблиц. При выполнении команды в диалоговом окне «Вставка таблицы» (рисунок 24) задаются параметры таблицы: количество строк, столбцов, их ширина, высота и так далее. После всех установок на экране появится таблица, в которую непосредственно вносится наполнение колонок. Для внесения текста нужно два раза «щелкнуть» внутри ячейки таблицы и набрать нужный текст.

Рисунок 24 – Диалоговое окно «Вставка таблицы»

Система AutoCAD позволяет выполнять следующие операции редактирования в таблицах:

Создание текстовых надписей. Кнопка на плавающей панели предусматривает написание многострочного текста. При выполнении этой команды необходимо определить размеры окна вставки текста, указав координаты первого и второго угла рамки. После этого появится диалоговое окно «Формат текста» (рисунок 25), в котором можно установить стиль, высоту текста, шрифт, вставить различные символы и т.д.

Рисунок 25 – Диалоговое окно «Формат текста»

В ниспадающей панели «Рисование» можно найти другой вариант написания текста: однострочный текст. На чертежах, как правило, надписей не так много, поэтому удобнее пользоваться командой «однострочный текст». При этом появляется сообщение о текущем стиле текста (Standard) и текущей высоте текста (2.5). Затем необходимо указать точку вставки текста либо мышью, либо ввести координаты на клавиатуре. После этого появится запрос о высоте текста и угле поворота. Когда появится надпись «Введите текст», можно вводить текст. Выход из команды – двойное нажатие клавиши «Enter».

В чертеже желательно иметь несколько текстовых стилей – для простановки размеров, для выполнения надписей.

Текстовый стиль определяется такими параметрами текста, как высота и имя шрифта, его начертание. Возможно изменение степени сжатия – растяжения текста, а также использование различных эффектов при создании надписей.

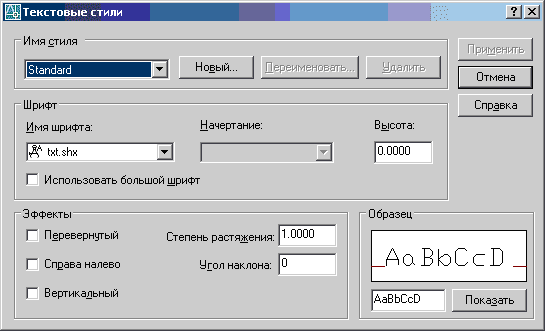
Создание новых и изменение имеющихся текстовых стилей выполняется при помощи команды «Текстовые стили» из падающего меню «Формат». При этом загружается диалоговое окно «Текстовые стили» (рисунок 41).

Нажатие кнопки «Новый» позволяет создать новый стиль текста, определив его имя, шрифт, начертание (курсив, обычный, полужирный). Можно задать, если это необходимо, угол наклона текста, а также различные эффекты. Например, сделать его перевернутым.

Рисунок 41 – Текстовые стили

Для того чтобы сделать стиль текущим, при выполнении команды «Многострочный текст», необходимо в диалоговом окне «Формат текста» выбрать его из списка. При выполнении команды «Однострочный текст» в командной строке выбрать опцию команды «Стиль» и ввести имя соответствующего стиля.

Команды «Блок» и «Создать блок» будут рассмотрены в теме №5

© ФГОУ ВПО «Красноярский государственный аграрный университет»

© Отдел информационных образовательных технологий

Источник