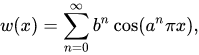что такое геометрическая кривая

Кривая

Кривая или линия — геометрическое понятие, определяемое в разных разделах геометрии различно.

Содержание

Элементарная геометрия

В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки и иногда определяется как «длина без ширины» или как «граница фигуры». По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и также трансцендентные кривые), применяя в каждом случае специальные приёмы.

Параметрические определения

Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:

При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если , путями.

Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые

и

эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) из отрезка на отрезок , такая что

Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.

Кривая Жордана

Кривой Жордана называется образ непрерывного инъективного отображения окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой или простой дугой.

Следует отметить что кривая Жордана является довольно сложным объектом, например, возможно построить плоскую кривую Жордана с ненулевой мерой Лебега.

Комментарий

Существует большой соблазн определить кривую как образ непрерывного отображения отрезка в пространство.

Однако возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат, например, кривая Пеано. Более того, согласно теореме Мазуркевича, компактное связное и локально связное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.

Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.

Аналитические кривые

Аналитическая кривая на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению , где является аналитической функцией. При этом на функцию накладываются ограничения, которые гарантируют, что

Аналогично определяются аналитические кривые в старших размерностях.

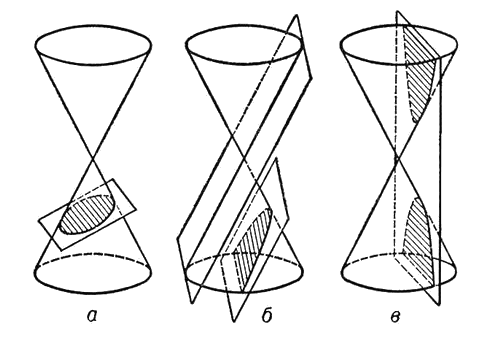
Алгебраические и трансцендентные кривые

Важный класс аналитических кривых составляют те, для которых функция есть многочлен от двух переменных. В этом случае кривая, определяемая уравнением , называется алгебраической, в противном случае — трансцендентной.

Алгебраические кривые, определяемые уравнениями высших степеней, рассматриваются в алгебраической геометрии. При этом бо́льшую стройность приобретает их теория, если рассмотрение ведется на комплексной проективной плоскости. В этом случае алгебраическая кривая определяется уравнением вида

,

где — однородный многочлен трех переменных, являющихся проективными координатами точек.

Более точно, трансцендентные кривые — кривые, которые можно задать через линию уровня аналитической функции (или, в многомерном случае, системы функций).

Типы кривых

Типы точек на кривой

Обобщённые кривые

Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:

Канторовой кривой называется компактное связное подмножество плоскости такое, что его дополнение всюду плотно.

Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая , она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество , гомеоморфное . Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.

Впоследствии это определение было обобщено Урысоном:

Кривой Урысона называется связное компактное топологическое пространство топологической размерности 1.

Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.

Источник

Прямые, кривые и очень изломанные. Краткая история линии от «Начал» Евклида до фракталов начала XX века

Что такое линия? Чем отличаются разные кривые друг от друга? Эти вопросы математики задают себе уже 2500 лет, и путь к ответам на них не лишен драматизма — открытие иррациональных длин отрезков было, по легенде, трагедией для мировоззрения пифагорейцев, а открытие заполняющих плоскость кривых Пеано в начале ХХ столетия заставило ученых пересмотреть свои представления о непрерывности и размерности пространства. Математик и художник Давид Кац — об истории понятия «кривая» в математике Античности и Средневековья и математическом анализе Нового времени.

Узоры древности

Интерес человека к прямым и искривленным линиям можно отследить с древнейших времен. Самые разные кривые мы видим в геометрических узорах на керамике и в архитектуре. Кроме достаточно простых узоров, составленных из прямых линий, часто можно встретить и что-то более сложное: спирали, волнистые линии и другие.

Представления о геометрии существовали уже в Египте и у цивилизаций Плодородного полумесяца. Возникли они, по-видимому, из совершенно практических потребностей: например, для сельского хозяйства важно уметь измерять площади участков земли. Однако в сохранившихся источниках мы видим эти представления скорее как набор рецептов, чем как науку.

Греция: длина без ширины

Древние греки подошли к вопросу более строго. В «Началах» Евклида возникают определения (впрочем, зачастую носящие скорее описательный характер — на них, например, не ссылаются далее) линии, прямой линии, точки. Выглядят они, мягко говоря, несовременно:

Определение 1.1. Точка — это то, часть чего есть ничто.

Определение 1.2. Линия — это длина без ширины.

Определение 1.3. Концы линий — это точки.

Определение 1.4. Прямая линия лежит равномерно по отношению к точкам на ней. (Или: Прямая линия есть та, которая равно лежит на всех своих точках.)

Первое из этих определений можно при желании трактовать в духе теории множеств, третье, по-видимому, намекает, что линии у нас априори конечные. Второе можно трактовать описательно, что касается четвертого, то мнения сильно расходятся.

Несколько иная, хотя местами и похожая ситуация возникает в труде, традиционно приписываемом Герону, — «Определение понятий геометрии» (но в статье W. R. Knorr, ‘Arithmêtikê stoicheiôsis’: on Diophantus and Hero of Alexandria, Historia Math. 20 (2) (1993), 180–192 приводятся аргументы в пользу принадлежности его Диофанту):

Прямая линия — это линия, которая одинакова по отношению ко всем точкам на ней, лежит прямо и максимально натянута между своими концами.

Последнее определение довольно явно отсылает нас к кратчайшему расстоянию между двумя точками.

Читайте также

В наиболее известных трудах древних греков рассматриваются главным образом прямые линии. Хотя в некоторых трудах встречаются и иные известные им линии.

Аполлоний Пергский, один из трех великих геометров Античности (вместе с Евклидом и Архимедом), занимался коническими сечениями. Об их существовании знали и до него, однако именно он дал им названия, закрепившиеся в науке, — эллипс, гипербола, парабола.

Приведем и несколько других примеров, известных грекам.

Знаменитая архимедова спираль:

Вторжение иррационального

Для пифагорейцев это была печальная новость — в рамках арифметики им такие числа не встречались, поэтому казалось, что и в целом вычисления с длинами оказывались под угрозой.

Интересно, что позже, в рукописи «Выпрямляющий кривое» (в рамках нашей статьи это предельно интригующее название — чуть позже станет понятно почему) некоего Альфонсо, предположительно, крещеного еврея, жившего в Испании между XIII и XV веками, к несоразмерности длин отношение уже гораздо более доброжелательное:

«Следует знать, что от ученых не скрыто то, как поступают люди, которые обвивают прямыми тонкими нитями из шелка, или льна, или другого материала скрепленный круг и измеряют его окружность прямой линией. Однако следует знать, будет ли на самом деле так, как это воспринимается чувством, которое обладает приблизительностью, ибо чувство недостаточно для этого при той приблизительности, которая имеется в нем. Ведь всякие две линии, не равные друг другу, можно разрезать на очень маленькие части так, что чувством будут их воспринимать как равноценные. Вместе с тем возможно, что эти величины несоизмеримы и что видов иррациональной меры бесконечное количество, как это доказано в 10-й книге Евклида».

Координаты и разрывы

Значительное развитие в понимании кривых линий произошло с переходом от геометрического описания к алгебраическому — в частности, к описанию кривых через уравнения.

В действительности нечто похожее на уравнение встречается у Архимеда и Аполлония Пергского — это так называемые симптомы конических сечений.

Затем координаты (в виде заимствованных из географии понятий долготы и широты) встречаются у Николая Орезмского во второй половине XIV столетия. В XVI веке Виет начал использовать символы для записи уравнений. И, наконец, Рене Декарт (синхронно с ним — Пьер де Ферма) развил идеи, совмещающие символьную запись уравнений и систему координат. Его труд пользовался огромной популярностью и быстро получил широкое распространение и существенное развитие. В системе координат появились отрицательные значения, саму сетку координат научились строить косоугольной.

Этот подход, хотя и ограниченно, применял Ньютон. Впоследствии Кеплер для представления траекторий движения планет активно использовал конические сечения в координатах, геометрически описанные еще греками.

Предыдущие шаги сформировали понятие алгебраической кривой — множества точек, чьи координаты связаны уравнением кривой.

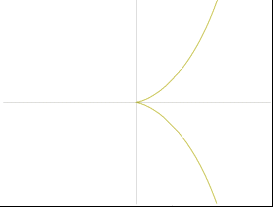
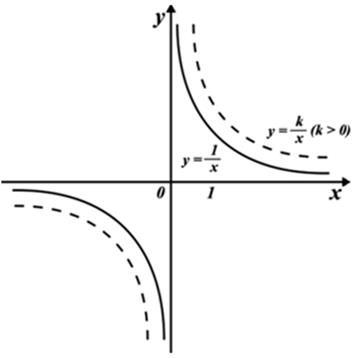
Интересно, что уже на этом, алгебраическом уровне возникают кривые с любопытными особенностями. Возьмем, например, известную многим со школы гиперболу — график функции 1/x. Его можно построить по точкам, но несложно сообразить, что уравнение y = 1/x имеет решение для любого x, кроме одного: x = 0 (на ноль делить нельзя). Это сказывается и на графике:

Что происходит в окрестности нуля? Нетрудно ответить. Давайте подойдем к нему справа. Когда мы подставляем в качестве x в выражение 1/x целое число больше 1, мы получаем дробь. Чем больше число, тем меньше получается дробь — этим и объясняется то, что график идет всё ниже и ниже по мере продвижения вправо. Подставляем х = 100, получаем у = 1/100, подставляет 1000000, получаем 1/1000000. Когда мы подставим в выражение единицу, на выходе получим единицу. Теперь пойдем в обратную сторону, ближе к нулю. Когда мы подставляем в выражение для y ½, она попадает в нижнюю часть дроби. Как мы помним, когда мы делим что-то на дробь, нам нужно умножить на перевернутую эту дробь. Значит, мы получим 2. Очевидно, чем ближе мы к нулю, тем сильнее уходим вверх — подставив 1/1000000, мы получим у = 1000000. Похожая ситуация при подходе слева, но с отрицательным знаком.

То, что происходит в нуле, называется разрывом (по виду графика хорошо понятно почему). В анализе принято классифицировать точки разрыва особым образом. То, что мы сейчас видели, называется точкой разрыва второго рода, поскольку односторонние пределы с двух сторон бесконечны (достаточно того, что один из них бесконечен). Если же односторонние пределы в точке разрыва конечны, то такая точка называется точкой разрыва первого рода.

Длина кривой

С самого начала людям хотелось описывать не только сами объекты, но и их свойства. И раз уж мы говорим о «длине, лишенной ширины», хотелось бы уметь эту длину считать. Мы хорошо умеем считать длины прямых отрезков при помощи линейки, которая позволяет нам определять расстояние между двумя точками, но когда дело касается кривых линий, нам нужен иной метод.

Мы расставляем n точек на равном расстоянии вдоль кривой, после чего замеряем длину прямых отрезков между этими точками (это мы делать умеем). Интуитивно возникает подозрение, что с увеличением числа n мы будем приближаться к значению настоящей длины — прирост суммы будет всё меньше, сверху он ограничен настоящей длинной кривой.

Для простых примеров — скажем, окружностей, синусоид, парабол — этот подход отлично работает. Примеры, в которых он дает сбой, мы рассмотрим далее.

Гладкость

Еще одним свойством, характеризующим кривые, является гладкость. Хотя смысл слова интуитивно понятен, задать ее математически не совсем элементарно. Мы хотим, чтобы у кривой не было углов, заострений, клювов и т. п.

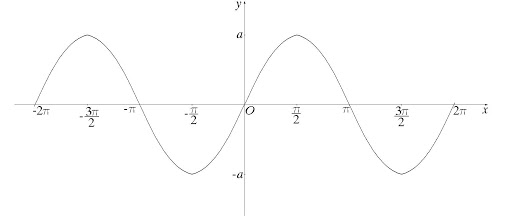
Хороший пример гладкой кривой — синусоида:

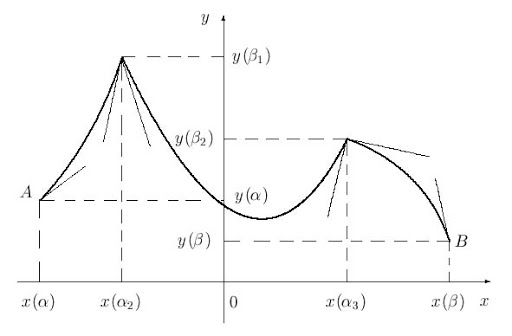
А вот пример негладкой кривой:

Чтобы определить это свойство, разберемся, что оно означает геометрически. Для начала вспомним концепцию касательной. Обычно в школе рассматривают в первую очередь касательные окружностей и определяют их как прямые, имеющие одну общую точку с окружностью. В случае произвольной кривой рассматривается касательная в локальном смысле — пересечения кривой вне некоторой окрестности точки касания не рассматриваются как проблема.

В курсе начал анализа доказывается, что такая касательная неразрывно связана с производной функции, график которой образует нашу кривую: более конкретно — тангенс угла наклона касательной (по отношению к положительному направлению оси Ox) равен значению производной функции в точке касания.

Может быть интересно

Кажется, что гладкость — довольно естественное требование к кривой. Это ощущение привело к тому, что в 1806 году Андре-Мари Ампер выдвинул гипотезу о том, что любая функция всюду, за исключением отдельных, «исключительных и изолированных» точек, имеет производную в этих точках.

Позднее гипотеза была разрушена. Первый контрпример следует атрибутировать, по-видимому, Бернхарду Риману. Более простой и широко известный контрпример был построен Ван дер Варденом позднее, в 1930 году. Но наибольшей известностью пользуется функция Вейерштрасса, выраженная формулой:

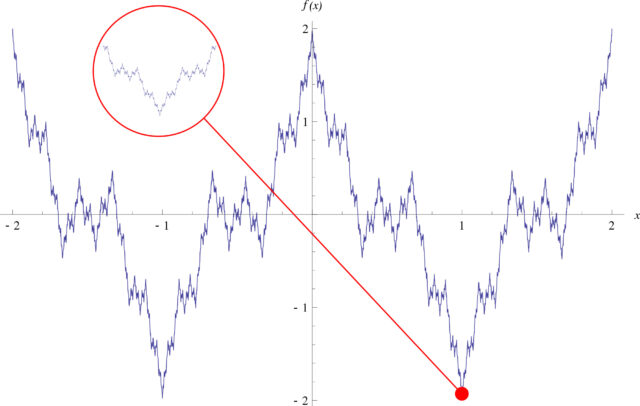
здесь a — любое нечетное число кроме единицы, b — число от нуля до единицы, а большая греческая cигма обозначает суммирование. Функция оказывается непрерывной для всех вещественных х, но при ряде условий на a и b очень негладкой:

Бесконечность в глубине отрезка

Совсем другой подход к кривым предложил великий французский математик Мари Энмон Камиль Жордан. Что если мы возьмем все точки отрезка и с помощью некоторого отображения перенесем их в пространство? Представьте, что наш отрезок сделан из проволоки, которую можно гнуть, вытягивать и сжимать. С помощью сжатия и вытягивания мы можем добиться изменения длины нашего отрезка, а с помощью сгибания — изменения его формы. Если же строго, то жордановой дугой называется образ непрерывного вложения отрезка в пространство: то есть разные точки отрезка обязательно перейдут в разные точки кривой. Можно представить, что отрезок у нас — временной, скажем, от начала работы секундомера до конца его работы. Тогда каждую секунду мы переводим в какое-то положение точки.

Жордановой замкнутой кривой называют образ непрерывного вложения окружности в пространство (из накладываемых требований следует, что окружность обязательно перейдет в некоторую замкнутую линию).

И хотя концепт жордановой кривой кажется достаточно простым, с его помощью можно получить весьма парадоксальные результаты.

В 1903 году Уильям Фогг Осгуд рассмотрел кривую, которая, являясь жордановой кривой, заполняет собой квадрат и в некоторых своих частях (более строго — порциях) имеет ненулевую площадь.

Впоследствии Кнопп построил жорданову кривую, обладающую ненулевой площадью вдоль всей кривой. Этот результат достигается за счет очень узких вырезаемых «клиньев», узость которых приводит к тому, что вычитаемая из площади треугольника площадь падает экспоненциально.

Кстати, вот здесь можно построить ее самостоятельно.

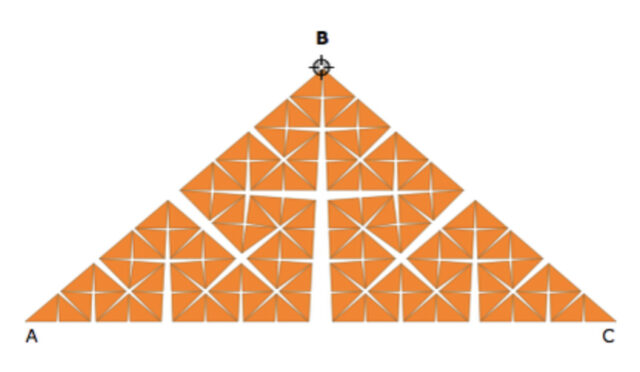
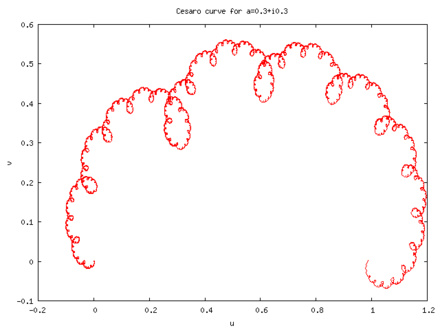
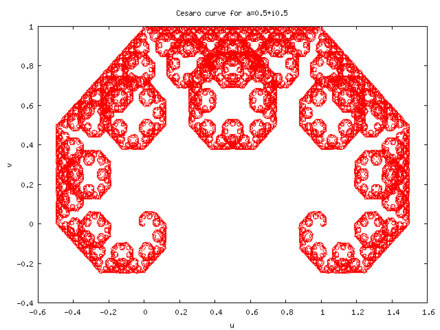
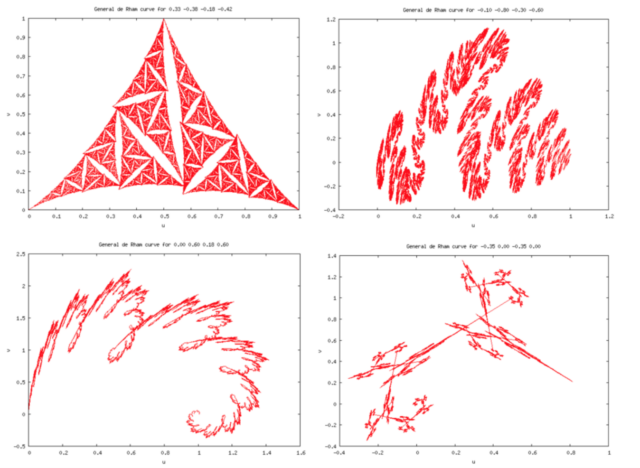
Примеров на эту тему много. Здесь мы упомянем полученные аффинными преобразованиями кривые де Рама:

кривую Коха — Пеано

и еще несколько кривых де Рама:

Заполнить плоскость

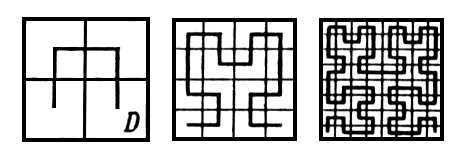
В 1890 году итальянский математик Джузеппе Пеано построил непрерывную кривую, которая проходит через любую точку квадрата (в оригинале использовался единичный, но построение легко повторить для квадрата любых размеров). Пеано задавался вопросом: может ли кривая заполнить всю плоскость или пространство? Результат Пеано воспринимался контринтуитивно. Годом позже кривую с тем же свойством построил уже графически Давид Гильберт.

В дальнейшем все кривые со свойством «заполнения» квадрата стали называть кривыми Пеано, а в более узком смысле это название закрепилось за конкретной кривой из его статьи 1890 года. Поскольку кривая заполняет любой наперед заданный квадрат, мы можем использовать ее и для заполнения плоскости, а в более общем случае — пространства или пустоты внутри нас.

Здесь нужно сделать важное уточнение — отображение с отрезка на квадрат, построенное Пеано, не взаимно-однозначно: не существует кривых Пеано, в которых каждая точка квадрата проходится только единожды — везде при этом построении возникают кратные точки.

Однако существуют кривые Пеано, у которых каждая точка проходится не более трех раз (и множество таких точек счетно).

Интересный факт следует из наших построений. Можно задать параметрически пространственную дугу, которая при проецировании на горизонтальную плоскость будет давать сплошное пятно; при этом такая «крыша» будет давать тень от вертикальных лучей света, но не спасет от дождя, поскольку ее поверхность получается не сплошной.

Ни одна кривая Пеано не гладкая. На интуитивном уровне можно объяснить это необходимостью очень быстро разворачивать направление нашей кривой, что невозможно сделать гладко. Сам Пеано в первой работе на эту тему сознательно не приводил построение кривой, чтобы не опираться на рисунок, однако мы всё же приведем это построение:

Обратите внимание на клетки, они позволяют понять, что происходит на каждом участке. То, что получится в результате бесконечного процесса этого рода, и называется кривой Пеано.

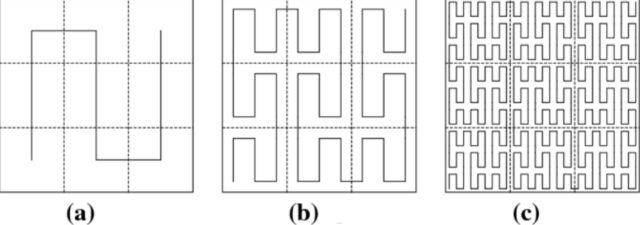
Обладающую тем же свойством кривую построил и современник Пеано Гильберт. Его кривая строится следующим образом:

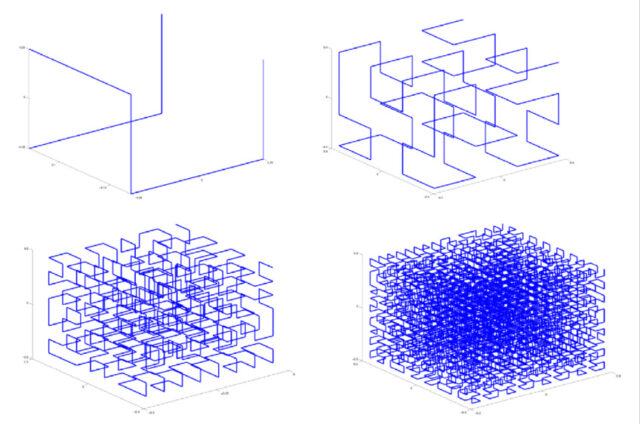
Существуют и объемные, и многомерные аналоги кривой Пеано, заполняющие куб (многомерный куб, соответственно).

Приведем несколько примеров других кривых, обладающих этим свойством.

Фракталы

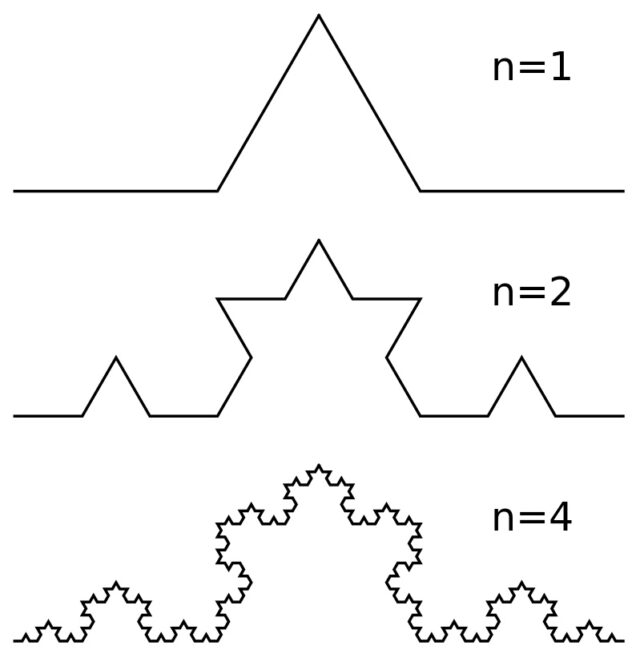
Подробнее об этом виде кривых мы писали тут. Однако в рамках разговора об эволюции представлений о кривых не упомянуть их невозможно. Классическим примером фрактала (фигуры со свойством самоподобия) является кривая Коха.

Свойство самоподобия означает, что фигура полностью или приближенно совпадает по форме с частью самой себя. В качестве примера можно провести кривую Коха:

В качестве нулевого «поколения» берем просто отрезок. На первом шаге его среднюю треть превращаем в правильный треугольник без основания, как бы выгибаем его. У нас получится четыре соединенных в кривую линию отрезка. На следующем шаге повторяем эту операцию с каждым из четырех отрезков. И так далее до бесконечности.

Читайте также

Наш подход с прямыми отрезками терпит здесь фиаско — вместо приближения к какой-то конечной длине сумма длин отрезков неограниченно растет.

Конечно, кривые, обладающие этим свойством, не исчерпываются самоподобными фигурами. Достаточно найти трещину на стене не самой простой формы: самоподобия в ней мы, как правило, не наблюдаем, и в то же время от одной ее «ветки» отходят новые, иной формы, и т. д.

Интересно, что тотально (то есть на любой порции) неспрямляемая кривая очень плохо помещается в ту же концепцию кривой как траектории движения. Точка, движущаяся по такой траектории, очевидно движется не по законам классической механики.

Во-первых, если бы точка двигалась с конечной скоростью по такой кривой, то она бы не двигалась вовсе: сколь угодно малая дуга здесь имеет бесконечную дугу. Но более того — такая кривая нигде не имеет и касательной, а значит, и направление скорости не задано!

В этом кратком обзоре мы лишь немного коснулись трансформации интуитивного представления о кривой в анализе — оставив за скобками развитие этого понятия в алгебре или современной геометрии, равно как и все вопросы, связанные с исследованием строения кривых.

Если эти — опущенные здесь — вопросы заинтересовали вас, то рекомендуем обратиться, например, к популярной брошюре В. И. Арнольда «Вещественная алгебраическая геометрия», а также к брошюре В. В. Острика и М. А. Цфасмана «Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые».

Источник