что такое генетический алгоритм
Что такое генетические алгоритмы
Естественный отбор
Процесс естественного отбора начинается с выбора сильных особей из популяции. Их потомство наследует характеристики родителей и является частью следующего поколения особей. Если оба родителя сильные, то их потомство будет сильнее родителей.
Это итеративный процесс и завершается, когда найдены наиболее сильные особи. Эта идея применяется для задачи поиска. Рассматривается набор решений для проблемы и отбирается набор лучших из них.
5 шагов генетического алгоритма
Процесс обучения генетического алгоритма делится на 5 этапов:
В генетическом алгоритме набор генов особи представлен в виде бинарной строки. Закодированная комбинация генов называется хромосомой.
Популяция, хромосомы и гены
Функция силы
Функция силы определяет, насколько сильна отдельная особь. Сила определяется как способность особи конкурировать с остальными особями по заданной метрике. Функция присваивает каждой особи уровень силы. Вероятность того, что особь будет выбрана для произведения следующей популяции, основывается на уровне силы особи.
Отбор
Идея отбора заключается в том, чтобы отобрать наиболее сильных особей и передать их гены следующему поколению особей. N пар особей (родители) отбирается на основании их силы.
Скрещивание
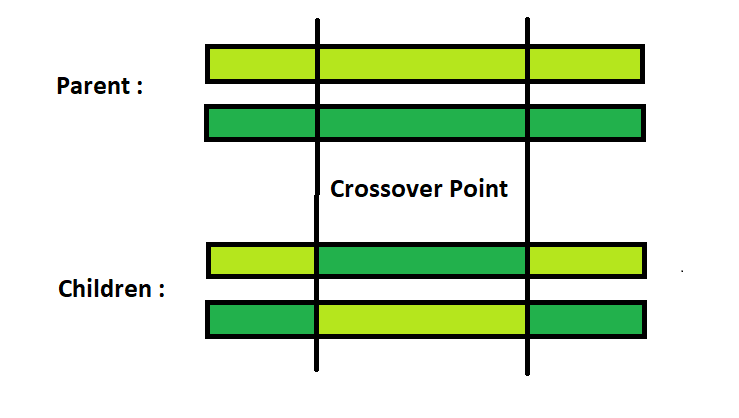
Скрещивание — это основная часть генетического алгоритма. Для каждой пары родителей. Рандомно выбирается точка в бинарной строке хромосомы, до которой особи обмениваются генами. После этого модифицированные особи называются потомством.
Точка скрещивания
Потомство создается через процесс обмена генами родителей до случайно заданной позиции в строке. Ниже можно увидеть, как родители обмениваются генами, когда точка скрещивания = 3.
После обмена генами между родителями потомство добавляется в новую популяцию.
Мутация
Какая-то часть генов будет маловероятной. Чтобы поддерживать разнообразие популяции, отдельно прописывается процесс мутации новых особей.

Завершение алгоритма
Алгоритм завершает работу, когда популяция сошлась, то есть не производит потомство, которое значительно отличается от предыдущего поколения. Когда алгоритм сошелся, на выходе получается набор оптимальных решений заданной проблемы.
Псевдокод процесса обучения генетического алгоритма:
Генетические алгоритмы в глубоком обучении
Генетические алгоритмы. От теории к практике
Добрый день. В последнее время решил заняться самообразованием. Решено было начать с генетических алгоритмов.
Одно из замечатльных свойств ГА это то, что процедуры Селекции, Скрещивания и Мутации представления не имеют о Индивидах в Поколениях — для них это всего-лишь 0 и 1. Единстенная функция, которая знает, что же из себя представляют эти самые 0 и 1 — это ФитнессФункция.
Поэтому я решил, что было бы неплохо написать класс-каркас для любого ГА. Об это и будет данная статья. Предполагается, что вы уже знакомы с основами генетических алгоритмов.
Кому интресно, прошу под кат.
Код будет написан на Java.
Несмотря на то, что мы пишем каркас, нам нобходимо его тестировать. Для этого я взял классическую NP-полную задачу — задачу коммивояжёра.
Немного об архитектуре приложения:
Для представления Генома(Индивида) будем использовать long[]. Мне почему-то показался этот вариант лучше чем boolean[].
Так же нам необходим интерфейс:
Разрабатываемый нами класс:
Так как мы пишем «универсальный» класс, необходимо, чтобы он поддреживал разные варианты скрещивания и селекции, поэтому были добавлены 2 перечисления (Enum):
… и некоторые приватные поля:
Для них есть сеттеры и геттеры.
А теперь о всем по порядку…
Генерация первого поколения.
Все очень просто: рандомом генерируем лонги, из лонгов составляем геномы и кладем их в массив. Код приводить не буду.
Селекция.
Несколько замечаний «от себя»:
Скрещивание.
Несколько замечаний «от себя»:
*Для функция скрещивания и мутации я использовал бинарные операции. Поэтому пришлось объявить несколько статических перменных.
Функция для скрещивания двух геномов:
(Приведн код только для Поэлементное Скрещивание)
Пояснения:
Чтобы обменять между собой числа a и b необходимо:
swapMask = a xor b;
a = a xor swapMask;
b = b xor swapMask;
А если на swapMask мы наложим (and) mask, то у a и b поменяются только те биты, которые == 1 в числе mask.
swapMask = (a xor b) and mask;
a = a xor swapMask;
b = b xor swapMask;
Мутация.
Чтобы инвертировать бит необходимо:
bit = bit xor 1;
Следовательно, чтобы инвертировать любой бит в числе необходимо сдвинуть единицу на нужную позицию.
И основная функция, которая связывает все предыдущие:
Применение.
Использовать это все достаточно просто:
Сначала нужно описать класс ФитнессФункции.
А дальше…
Вернемся к задаче коммивояжёра.
Так как растояние между городами заполнялось рандомом «random.nextInt(256)». То смею предположить, что среднее расстояние между 2 городами = 128. => Средняя длина маршрута по всем городам = 128*256=32768. (! могу ошибаться).
ГА находит путь = 10000-12000 за 6-7 сек. Что в 3 раза лучше Среднего.
5500-7000 за минуту.
Код работает около 15 часов. и находит маршрут = 3500-4000.
Куда расти дальше.
UPD2:LeoCcoder нашел ошибку в Рулетке(в бинарном поиске). Исправлено.
Генетический алгоритм — наглядная реализация
Года четыре назад, в универе услышал о таком методе оптимизации, как генетический алгоритм. О нем везде сообщалось ровно два факта: он клёвый и он не работает. Вернее, работает, но медленно, ненадежно, и нигде его не стоит использовать. Зато он красиво может продемонстрировать механизмы эволюции. В этой статье я покажу красивый способ вживую посмотреть на процессы эволюции на примере работы этого простого метода. Нужно лишь немного математики, программирования и все это приправить воображением.
Кратко об алгоритме
Итак, что же такое генетический алгоритм? Это, прежде всего, метод многомерной оптимизации, т.е. метод поиска минимума многомерной функции. Потенциально этот метод можно использовать для глобальной оптимизации, но с этим возникают сложности, опишу их позднее.
Сама суть метода заключается в том, что мы модулируем эволюционный процесс: у нас есть какая-то популяция (набор векторов), которая размножается, на которую воздействуют мутации и производится естественный отбор на основании минимизации целевой функции. Рассмотрим подробнее эти процессы.
Итак, прежде всего наша популяция должна размножаться. Основной принцип размножения — потомок похож на своих родителей. Т.е. мы должны задать какой-то механизм наследования. И лучше будет, если он будет включать элемент случайности. Но скорость развития таких систем очень низкая — разнообразие генетическое падает, популяция вырождается. Т.е. значение функции перестает минимизироваться.
Для решения этой проблемы был введен механизм мутации, который заключается в случайном изменении каких-то особей. Этот механизм позволяет привнести что-то новое в генетическое разнообразие.
Следующий важный механизм — селекция. Как было сказано, селекция — отбор особей (можно из только родившихся, а можно из всех — практика показывает, что это не играет решающую роль), которые лучше минимизируют функцию. Обычно отбирают столько особей, сколько было до размножения, чтобы из эпохи в эпоху у нас было постоянное количество особей в популяции. Также принято отбирать «счастливчиков» — какое-то число особей, которые, возможно, плохо минимизируют функцию, но зато внесут разнообразия в последующие поколения.
Этих трех механизмов чаще всего недостаточно, чтобы минимизировать функцию. Так популяция вырождается — рано или поздно локальный минимум забивает своим значением всю популяцию. Когда такое происходит, проводят процесс, называемый встряской (в природе аналогии — глобальные катаклизмы), когда уничтожается почти вся популяция, и добавляются новые (случайные) особи.
Вот описание классического генетического алгоритма, он прост в реализации и есть место для фантазии и исследований.
Постановка задачи
Итак, когда я уже решил, что хочу попробовать реализовать этот легендарный (пусть и неудачливый) алгоритм, речь зашла о том, что же я буду минизимировать? Обычно берут какую-нибудь страшную многомерную функцию с синусами, косинусами и т.д. Но это не очень интересно и вообще не наглядно. Пришла одна незатейливая идея — для отображения многомерного вектора отлично подходит изображение, где значение отвечает за яркость. Таким образом, мы можем ввести простую функцию — расстояние до нашего целевого изображения, измеряемое в разности яркости пикселей. Для простоты и скорости я взял изображения с яркостью 0, либо 255.
С точки зрения математики такая оптимизация — сущий пустяк. График такой функции представляет собой огромную многомерную «яму» (как трехмерный парабалоид на рисунке), в которую неизбежно скатишься, если идти по градиенту. Единственный локальный минимум является глобальным. 
Проблема только в том, что уже близко к минимуму количество путей, по которым можно спуститься вниз сильно сокращается, а всего у нас столько направлений, сколько измерений (т.е. количество пикселей). Очевидно, что решать эту задачу при помощи генетического алгоритма не стоит, но мы можем посмотреть на интересные процессы, протекающие в нашей популяции.
Реализация
Были реализованы все механизмы, описанные в первом параграфе. Размножение проводилось простым скрещиванием случайных пикселей от «мамы» и от «папы». Мутации производились путем изменения значения случайного пикселя у случайной особи на противоположное. А встряска производилась, если минимум не меняется на протяжении пяти шагов. Тогда производится «экстремальная мутация» — замена происходит более интенсивно, чем обычно.
В качестве исходных картинок я брал нонограмы («японские сканворды»), но, по правде говоря, можно брать просто черные квадраты — нет абсолютно никакой разницы. Ниже показаны результаты для нескольких изображений. Здесь для всех, кроме «домика», количество мутаций было 100 в среднем на каждую особь, особей в популяции было 100, при размножении популяция увеличивалась в 4 раза. Счастливчиков было 30% в каждой эпохе. Для домика значения были выбраны меньшие (30 особей в популяции, мутаций по 50 на особь).


Экспериментально я установил, что использование «счастливчиков» в селекции понижает скорость стремления популяции к минимуму, но зато помогает выбираться из стагнации — без «счастливчиков» стагнация будет постоянна. Что можно увидеть из графиков: левый график — развитие популяции «фараона» со счастливчиками, правый — без счастливчиков.
Таким образом, мы видим, что этот алгоритм позволяет решить поставленную задачу, пусть и за очень долгое время. Слишком большое количество встрясок, в случае больших изображений, может решить большее количество особей в популяции. Оптимальный подбор параметров для разных размерностей я оставляю за рамками данного поста.
Глобальная оптимизация
Как было сказано, локальная оптимизация — задача довольно тривиальная, даже для многомерных случаев. Гораздо интересней посмтреть, как будет алгоритм справляться с глобальной оптимизацией. Но для этого нужно сначала построить функцию со множеством локальных минимумов. А это в нашем случае не так сложно. Достаточно брать минимум из расстояний до нескольких изображений (домик, динозаврик, рыбка, кораблик). Тогда первоначальный алгоритм будет «скатываться» в какую-то случайную ямку. И можно просто запускать его несколько раз.
Но есть более интересное решение данной проблемы: можно понять, что мы скатились в локальный минимум, сделать сильную встряску (или вообще инициировать особи заново), и в дальнейшем добавлять штрафы при приближении к известному минимуму. Как видно, картинки чередуются. Замечу, что мы не имеем права трогать исходную функцию. Но мы можем запоминать локальные минимумы и самостоятельно добавлять штрафы.
На этой картинке изображен результат, когда при достижении локального минимума (сильная стагнация), популяция просто вымирает.
Здесь популяция вымирает, и добавляется небольшой штраф (в размере обычного расстояния до известного минимума). Это сильно снижает вероятность повторов.
Более интересно, когда популяция не вымирает, а просто начинает подстрариваться под новые условия (след. рисунок). Это достигается при помощи штрафа в виде 0.000001 * sum ^ 4. В таком случае, новые образы становятся немного зашумлены:
Этот шум устраняется путем ограничения штрафа в max( 0.000001 * sum ^ 4, 20). Но мы видим, что четвертого локального минимума (динозавра) достичь не удается — скорее всего, потому, что он слишком близко расположен к какому-то другому.
Биологическая интерпретация
Какие же выводы мы можем сделать из, не побоюсь этого слова, моделирования? Прежде всего, мы видим, половое размножение — важнейший двигатель развития и приспосабливаемости. Но только его не достаточно. Роль случайных, маленьких изменений чрезвычайна важна. Именно они обеспечивают возникновение новых видов животных в процессе эволюции, а у нас обеспечивает разнообразие популяции.
Важнейшую роль в эволюции Земли играли природные катаклизмы и массовые вымирания (вымирания динозавров, насекомых и т.д. — крупных всего было около десяти — см. диаграмму ниже). Это было подтверждено и нашим моделированием. А отбор «счастливчиков» показал, что самые слабые организмы на сегодня способны в будущем стать основой для последующих поколений.
Как говорится, все как в жизни. Этот метод «сделай эволюцию сам» наглядно показывает интересные механизмы и их роль в развитии. Конечно, существует много более стоящих эволюционных моделей (основанных, конечно, на дифурах), учитывающих больше факторов, более приближенные к жизни. Конечно, существуют более эффективные методы оптимизации.
Писал программу на Matlab (вернее, даже на Octave), потому что тут все — голимые матрицы, и есть инструменты для работы с картинками. Исходный код прилагается.
Искусственный интеллект. Генетический алгоритм и его применения
„Выживает не самый сильный и не самый умный, а тот, кто лучше всех приспосабливается к изменениям.“
Чарльз Дарвин
“Даже если у одного прочитавшего из тысячи появится интерес к этим алгоритмам, и он решит углубиться — это уже отлично.”
Внимание, вопрос: помните ли вы движущие силы эволюции по Дарвину? Эти знания нужны для понимания работы генетического алгоритма, так как он пытается имитировать процессы, действительно происходящие в природе. Итак, основной предпосылкой эволюции является наследственная изменчивость, а её движущими силами — борьба за существование и естественный отбор. Используя генетический алгоритм, вы действуете по сути как творец и сами устанавливаете законы эволюции, позволяющие достичь оптимальности в популяции. В идеале должны выработаться необходимые для выживания и адаптации качества, которые и будут искомым решением. Посмотрим, как реализуются эти принципы в генетическом алгоритме.
⇡#Что это?
Генетический алгоритм (ГА) — это алгоритм поиска и оптимизации, прообразом которого стал биологический принцип естественного отбора.
⇡#Как он работает?
Первый этап — создание популяции. В данном случае популяция — это не совокупность биологических особей, а множество возможных решений имеющейся проблемы, которые образуют пространство поиска (space search).
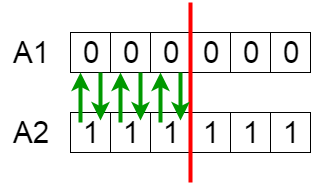
Второй этап — подсчёт функции пригодности (приспособленности, fitness function). Данная функция принимает на вводе потенциальное решение проблемы (candidate solution), а выдаёт значение, оценивающее его пригодность. В случае с классическим генетическим алгоритмом целевая функция и функция пригодности — это одно и то же. Далее проверим, выполнено ли условие остановки алгоритма. Алгоритм прекратит исполняться, если достигнуто ожидаемое оптимальное значение, если полученное значение больше не улучшается или по истечении заданного времени/количества итераций. После остановки происходит выбор самой приспособленной хромосомы (по наибольшему значению функции). Если же условие остановки не выполнено, то по результатам естественного отбора будет производиться селекция хромосом для производства потомков.
Третий этап – скрещивание ( в русских источниках — «кроссинговер», реже «кроссовер» ) и мутация.
Блок-схема генетического алгоритма
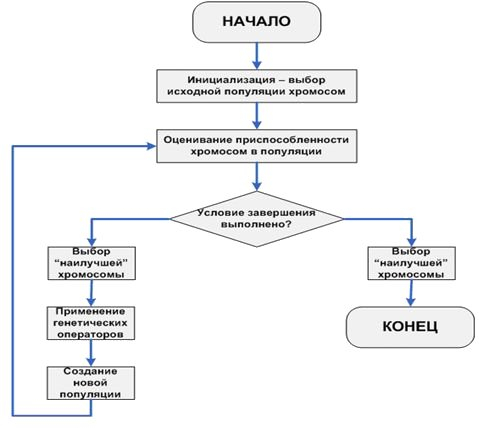
Скрещивание, мутация и селекция – это генетические операторы. Как и в природе, вероятность скрещивания на несколько порядков выше вероятности мутации. Скрещивание поддерживает бесконечное разнообразие в популяции, это перераспределение генетического материала родителей, благодаря которому у потомков появляются новые сочетания генов. Но о каких «генах» и «хромосомах» может идти речь вне контекста живой природы? В генетическом алгоритме «хромосома» — набор параметров, определяющих предлагаемое возможное решение, а «ген» — это одна из «букв» строки «хромосомы», как правило, имеющая двоичное значение. Как мы помним, в результате селекции отбираются самые приспособленные хромосомы — к ним и применяются эти генетические операторы. Наверное, вы сейчас думаете, каким же образом может происходить скрещивание у таких «хромосом». Возможно несколько сценариев, упомянем лишь некоторые из них.
Одноточечный кроссинговер (single-point crossover): есть пара родительских хромосом с набором генов L, для них случайным образом выбирается так называемая точка скрещивания Px – это некая позиция гена в хромосоме. К [1; Px] одной родительской хромосомы присоединяется [Px+1; L] другой, и получается первый потомок. Второй потомок получается также скрещиванием, но «в обратную сторону».
Двухточечный кроссинговер (two-point crossover): обмен генетическим материалом, (то есть, битами) происходит в двух точках скрещивания.
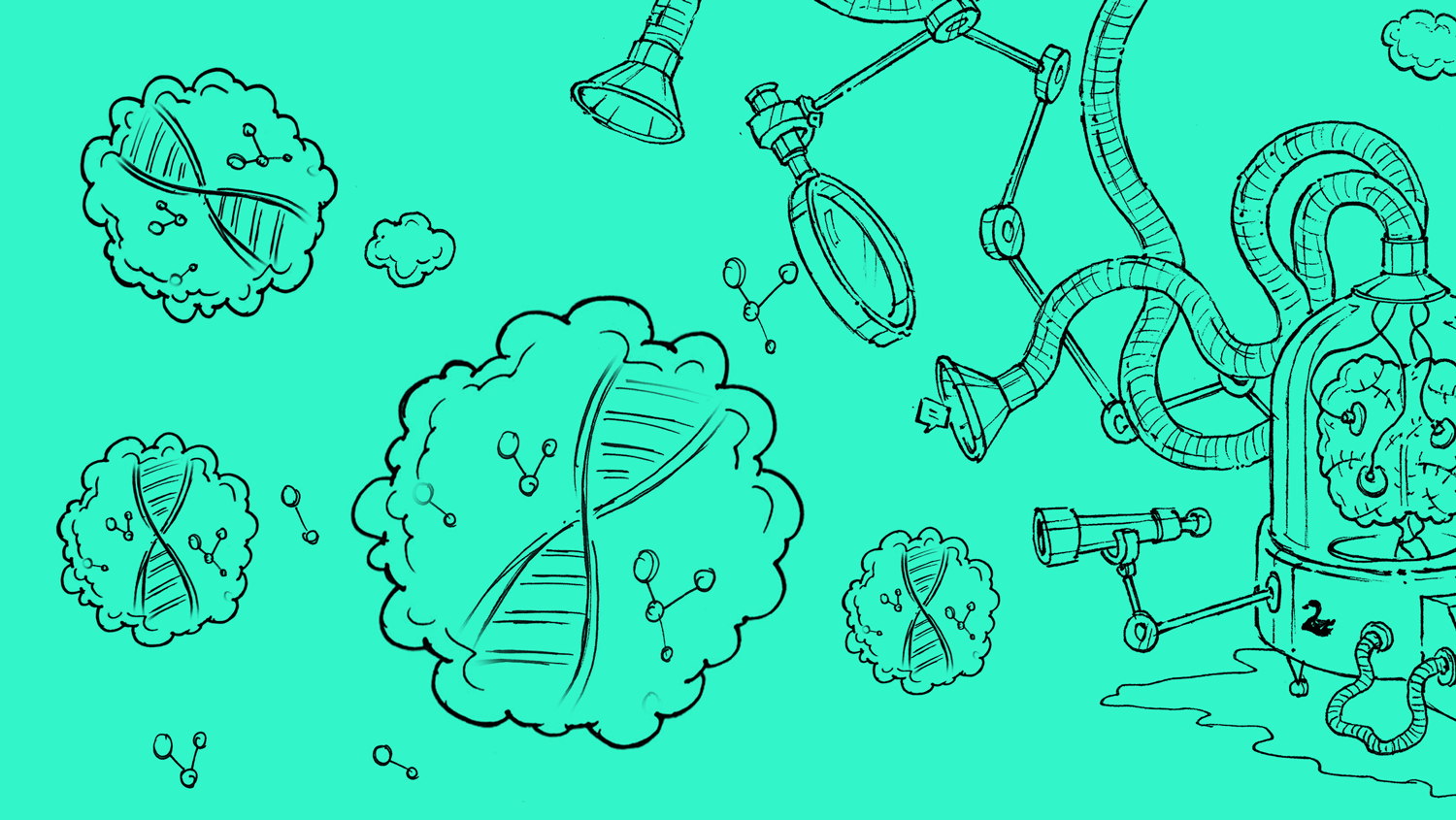
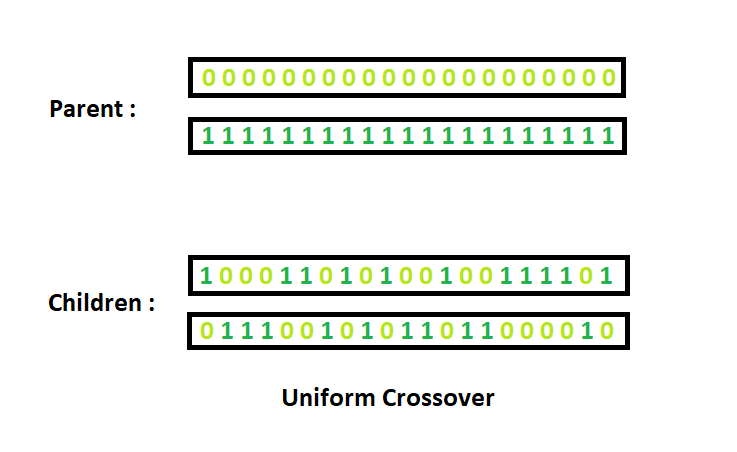
Однородный кроссинговер (uniform crossover): значение каждого бита в хромосоме потомка определяется согласно случайно сгенерированной маске кроссинговера. Если в маске стоит 0 – берется ген от первого родителя, если 1 – от второго.
Для более глубокого погружения в тему эволюционных алгоритмов реокмендуем изучить статью F.Herrera, M.Losano, A.M.Sanches Hybrid Crossover Operators for Real-Coded Genetic Algorithms: An Experimental Study.
Мутация — генетический оператор, который с некой вероятностью меняет один или несколько «генов» в случайных позициях «хромосомы». Для чего он нужен? Зачем мутации (изменения в генетическом коде) существуют в природе, могут ли они способствовать лучшей выживаемости вида? Эта статья не о генетике, но не будем забывать, что именно она послужила источником вдохновения для Холланда, создателя генетического алгоритма (1975). Потомки, которые подверглись воздействию генетических операторов, образуют новую популяцию – и в ней начинается очередная итерация ГА. Снова идет подсчет функции пригодности, происходит естественный отбор, а дальше алгоритм либо остановится, если заданное условие выполнено, либо вновь перейдет к селекции. Если хочется посмотреть интересное применение, можно почитать разбор задачи коммивояжера (travelling salesman problem) и задачи об укладке рюкзака (knapsack problem) с применением ГА. Обе эти задачи являются задачами комбинаторной оптимизации, то есть в конечном множестве объектов мы ищем оптимальный. Сами того не подозревая, мы решаем подобные задачи каждый день. Теперь посмотрим на преимущества и недостатки этого метода.
Плюсы ГА
Этот алгоритм имеет уникальные сильные стороны:
Минусы ГА
⇡#Для каких задач используется ГА?
С помощью ГА решается ц елый спектр задач: от разработки антенн NASA до программ распознавания структуры белков.
В финансах ГА успешно используется для моделирования экономических агентов с ограниченно рациональным поведением: финансового прогнозирования, инвестирования, и т. д. Одна из интересных задач — оптимизация финансового портфеля (portfolio optimization). В теории игр ГА применяется, например, для разрешения дилеммы узника. Его можно применять в играх с двумя участниками для оптимизации стратегий.
В робототехнике ГА прекрасно применяется для управления человекоподобным роботом, оптимизации планирования маршрута (routing). В авиации — для системы контроля полетов. Кстати об авиации: ученые General Electric и Ренсселеровского политехнического института применили ГА для конструирования турбины реактивного двигателя, который применяется в современных авиалайнерах.
Можно использовать ГА и в более близких для нас ситуациях, например, для планирования расписания на производстве или в крупном учебном заведении. В первом случае фитнес-функция может задавать количество деталей, изготовленных за определенное количество времени, а во втором – «штрафовать» конфликтующие ветки расписания. Возможности для творчества просто безграничны.
Что дальше? Читатель, который хочет знать больше, может обратиться к материалам GECCO conference — это конференция, которая посвящена эволюционному программированию, там самые горячие новости и обновления. Математическая сторона хорошо описана здесь:
Ещё по применениям ГА на английском языке:
Недавно вышла привлекающая внимание книга: Buontempo, Frances. Genetic algorithms and machine learning for programmers: create AI models and evolve solutions. Pragmatic Bookshelf, 2019.
Материалы, которые использовались для написания этой статьи:
Генетический алгоритм построения алгоритмов
В типичной реализации генетический алгоритм оперирует параметрами какой-то сложной функции (диофантовые уравнения в статье «Генетический алгоритм. Просто о сложном» mrk-andreev) или алгоритма («Эволюция гоночных автомобилей на JavaScript» ilya42). Количество параметров неизменно, операции над ними тоже изменить невозможно, как генетика не старается, потому что они заданы нами.
Хьюстон, у нас проблема
Сложилась странная ситуация — прежде чем применять генетические алгоритмы (ГА) к реальной задаче, мы сначала должны найти алгоритм, которым эта задача в принципе решается, и только потом его попытаться оптимизировать с помощью генетического алгоритма. Если мы ошиблись с выбором «основного» алгоритма, то генетика не найдет оптимум и не скажет, в чем ошибка.
А что, если. Если заставить ГА не оптимизировать параметры, а создавать другой алгоритм, наиболее подходящий для данной задачи. Вот этим я и занимался ради интереса.
Генотип из операций
Напомню, что генетические алгоритмы обычно оперируют т.н. «генотипом», вектором «генов». Для самого ГА не имеет значения, чем будут являться эти гены — числами, буквами, строками или аминокислотами. Важно лишь соблюдение необходимых действий над генотипами — скрещивание, мутация, селекция — необязательно в этом порядке.
Так вот, идея в том, что «геном» будет элементарная операция, а «генотипом» — алгоритм, составленный из этих операций. Например, генотип, составленный из математических операций и реализующий функцию :
Тогда в результате выполнения ГА мы получим формулу или алгоритм, структуру которого мы заранее предсказать не можем.
Скрещивание фактически не меняется, новый генотип получает кусочки от каждого родителя.
Мутацией может быть замена одного из генов на какой-либо другой, то есть происходит замена одной операции в алгоритме и/или изменение параметров этой операции.
С селекцией и просто, и сложно одновременно. Поскольку мы создаем алгоритм, то самый простой способ его проверить — это выполнить его и оценить полученный результат. Так машинки своим продвижением по трассе доказывали оптимальность своей архитектуры. Но у машинок был четкий критерий — чем дальше она проехала, тем лучше. Наш же целевой алгоритм в общем случае может иметь несколько критериев оценки — длина (чем короче, тем лучше), требования к памяти (чем меньше, тем лучше), устойчивость к мусору на входе и т.д.
Кстати, у машинок критерий был один, но работал он только в пределах текущей трассы. Лучшая для одной трассы машинка вряд ли оказалась бы лучшей на другой.
А если подумать?
В процессе обдумывания, какие операции включить в словарь генов и как они должны работать, я понял, что нельзя ограничиваться операциями над одной переменной. Те же нейронные сети оперируют всеми (FNN) или несколькими (CNN) входными переменными одновременно, поэтому нужен способ задействовать в полученном алгоритме нужное количество переменных. Причем в какой операции какая переменная потребуется, я заранее предугадать не могу и не хочу ограничивать.
На помощь пришел… не угадаете… язык Forth. Точнее, обратная польская запись и стековая машина с их возможностью класть значения переменных на стек и выполнять операции над ними в нужном порядке. И без скобок.
Для стековой машины помимо арифметических операций нужно запрограммировать стековые операции — push (взять следующее значение со входного потока и положить на стек), pop (взять значение со стека и выдать в качестве результата), dup (сдублировать верхнее значение на стеке).
Просто do it!
Получился такой объект, реализующий один ген.
Это был первый вариант, в принципе рабочий, но с ним быстро выявилась проблема — для арифметических операций требовалось передавать значение, а для операций на стеке pop и dup — нет. Мне не хотелось различать вызываемые операции в вызывающем коде и определять, сколько нужно параметров передавать каждой из них, поэтому переделал — вместо одного значения value передавал массив входных значений, и пусть сама операция делает с ним что хочет.
Второй проблемой стало то, что арифметические операции оказались слишком требовательны — им нужно было и значение на стеке, и входное значение. В результате генетический алгоритм не мог сформировать ни один генотип. Пришлось разделить операции на работающие со стеком и на работающие с входным значением.
Ниже последняя версия.
С объектом генотипа пришлось немного повозиться, подбирая алгоритм скрещивания. Какой из них лучше, я так и не определился, оставил на волю псевдослучайности. Сам алгоритм был определен в методе умножения __mul__.
Для обоих классов переопределен метод __str__, чтобы выводить их содержимое в консоль.
Функция просчета алгоритма чуть подробнее:
Обратите внимание на закомментированный raise — первоначально у меня была идея, что генотип с алгоритмом, вылетающим по ошибке, не должен жить на этом свете и должен сразу отбраковаться. Но ошибок было слишком много, популяция вырождалась, и тогда я принял решение не уничтожать объект, а ампутировать его на этом гене. Так генотип становится короче, но остается рабочим, и его рабочие гены можно использовать.
Итак, есть генотип, есть словарь генов, есть функция скрещивания двух генотипов. Можно проверить:
Теперь нужны функции размножения (отбор и скрещивание лучших) и мутации.
Функции скрещивания и размножения генотипов до необходимого количества я написал в трех вариантах. Но худшая половина погибает в любом случае.
Функция мутации применяется к новому генотипу
Как можно применить такой генетический алгоритм?
Например:
— выявлять закономерность среди входных данных, регрессионный анализ
— выработать алгоритм, восстанавливающий выпадения в сигнале и убирающий помехи — полезно для речевой связи
— разделять сигналы, пришедшие от разных источников по одному каналу — полезно для голосового управления, создания псевдостерео
Для этих задач нужен генотип, который примет на вход массив входных значений и выдаст массив выходных значений той же длины. Я пробовал совмещать задачи получения подходящих генотипов и достижения цели, оказалось слишком сложно. Проще было прогнать генетику с целью отбора генотипов для начальной популяции, чтобы эти генотипы вообще смогли обработать входной массив.
Для отбора генотипов написана функция, она генерит генотипы, прогоняет их по ГА, отбраковывает по результату и возвращает массив выживших. ГА прекращается раньше времени, если популяция выродилась.
Функция оценки отклонения результата от искомого (не совсем фитнес-функция, т.к. чем больше отклонение, тем хуже генотип, но это учтем).
Ну и последний штрих — собственно ГА на отобранных генотипах.
Или, проще говоря, лучший результат ГА с целью destData = [10, 20, 30, 40, 50, 60] получился [9.571, 24.952, 30.989, 35.638, 50.462, 65.698]. Этого результата добивается генотип с алгоритмом (const:24.7735, addMem:1.7929, dup:39.1318, dup:-15.2363, mulVal:24.952, mulVal:4.7857, pop:14.4176, pop:19.8343, dup:-19.4728, pop:2.6658, dup:-14.8237, pop:6.7005, pop:1.3567, pop:-2.7399).
С одной стороны, алгоритм избыточен — он делает действия, ненужные для получения конечного результата. С другой — алгоритм ограничен, так как использует только два значения из входного потока из шести — понятно, что так получилось из-за ограниченных входных данных.