что такое гармоническая волна
Гармоническая волна
В разных случаях при необходимости особо выделяется интересующий класс гармонических волн, например, плоская гармоническая волна, стоячая гармоническая волна и т. д. (см. ниже).Источниками гармонических волн могут быть гармонические колебания, они также могут возбуждаться в какой-либо системе при взаимодействии её с гармонической волной.
Связанные понятия
Главным образом, интерес к вопросу распространения волн в случайно-неоднородных средах (какой является, например, атмосфера) можно объяснить бурным развитием спутниковых технологий. В этом случае становится важной задача расчета характеристик (например, амплитуды) волны прошедшей через среду и установления их связей с параметром неоднородности среды. Важную роль здесь и играет функция Грина для случайно-неоднородной среды, зная которую можно определить эти характеристики. Рассматривается прохождение.
В квантовой механике импульс, как и все другие наблюдаемые физические величины, определяется как оператор, который действует на волновую функцию.
Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой. Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость.
Фотоны, которые мигрируют в биологических тканях могут быть описаны при помощи численного моделирования методом Монте Карло или аналитическим уравнением переноса излучения (УПИ). Однако, УПИ трудно решается без применения упрощений (приближений). Стандартным методом упрощения УПИ является диффузионное приближение. Общее решение уравнения диффузии для фотонов получается быстрее, но менее точно чем методом Монте Карло.
Мультипо́ли (от лат. multum — много и греч. πόλος — полюс) — определённые конфигурации точечных источников (зарядов). Простейшими примерами мультиполя служат точечный заряд — мультиполь нулевого порядка; два противоположных по знаку заряда, равных по абсолютной величине — диполь, или мультиполь 1-го порядка; 4 одинаковых по абсолютной величине заряда, размещённых в вершинах параллелограмма, так что каждая его сторона соединяет заряды противоположного знака (или два одинаковых, но противоположно направленных.
Ниже приведены примеры уравнений непрерывности, которые выражают одинаковую идею непрерывного изменения некоторой величины. Уравнения непрерывности — (сильная) локальная форма законов сохранения.
Эта статья о физическом понятии. О более общем значении термина, см. статью СкалярСкалярная величина (от лат. scalaris — ступенчатый) в физике — величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д.Скалярная величина, или скаляр согласно математическому энциклопедическому словарю.
В математике особой точкой векторного поля называется точка, в которой векторное поле равно нулю. Особая точка векторного поля является положением равновесия или точкой покоя динамической системы, определяемой данным векторным полем: фазовая траектория с началом в особой точке состоит в точности из этой особой точки, а соответствующая ей интегральная кривая представляет собой прямую, параллельную оси времени.
Гармоническая волна
Слово ‘гармоническая’ тут является синонимом слова ‘монохроматическая’, однако, по-видимому, не совсем точным; во всяком случае, обычные области применения того и другого термина обычно несколько различаются.
Источниками гармонических волн могут быть гармонические колебания, они также могут возбуждаться в какой-либо системе при взаимодействии ее с гармонической волной.
Содержание
Одномерный случай
Случай одномерного однородного пространства (или одномерной однородной среды) [2] — наиболее прост.
В этом случае все виды гармонических волн сводятся к:
а также к конечным линейным комбинациям волн такого вида (для выражения произвольной действительной гармонической волн в этом случае достаточно смешать две волны первого вида или четыре второго; в случае более многомерного u добавляется по два таких слагаемых на каждую поляризацию).
Здесь A — постоянный (не зависящий от x и t) коэффициент, природа и размерность которого свпадает с природой и размерностью поля u; k, ω и φ0 — также постоянные параметры, в рассматриваемом одномерном случае все они — действительные числа (в отличие от более многомерных, где k становится векторным — для плоских волн). A — есть амплитуда волны, k — волновое число, ω — (циклическая) частота и φ0 — начальная фаза — то есть фаза волны при x = t = 0.
Во второй формуле A — (обычно) комплексное, амплитуду волны определяет его модуль |A|, а начальная фаза спрятана также в A в качестве его аргумента, поскольку
Так же, как стоячая волна выражается (как записано здесь) через две бегущих, так же и бегущая может быть выражена через две стоячих. Поэтому можно выбрать один из двух равноправных способов выражения произвольной гармонической волны в случае одномерного однородного пространства: через линейную комбинацию бегущих или линейную комбинацию стоячих волн. Это верно и для всех других случаев, хотя базисные волны, через линейную комбинацию которых выражается произвольная гармоническая волна, могут оказаться сложнее.
Случаи пространства размерностью больше единицы
В случаях пространства размерностью больше единицы, даже если оно однородно, в принципе разнообразие возможных гармонических волн очень сильно возрастает. Однако есть два типа гармонических волн, которым следует уделить главное отдельное внимание.
Плоские гармонические волны
наиболее важным и часто встречающимся типом гармонических волн являются плоские гармонические волны. (Одномерные гармонические волны являются их одномерным частным случаем.)
где, в отличие от одномерной волны 
— уже не действительное число, а вектор, называемый волновым вектором, размерность которого равна размерности пространства, а выражение 
означает скалярное произведения этого вектора с вектором [3] 
, характеризующим точку пространства: 
.
Легко видеть, что если выбрать ось координат вдоль волнового вектора, плоская многомерная волна сводится к одномерной (u вообще перестает зависеть от остальных координат, а от первой — зависит как одномерная гармоническая волна).
Так же, как и в одномерном случае, стоячие и бегущие гармонические волны одной частоты с одинаковым (быть может, с точностью до знака) волновым вектором, элементарно линейно выражаются друг через друга.
Поскольку с помощью преобразования Фурье (в текущем параграфе подразумевается, конечно, многомерное преобразование Фурье) практически любую [4] функцию пространственных координат можно представить как сумму (интеграл) функций, представляющих каждая плоскую волну, а зависимость от времени в тогда для случая однородного пространства будет тоже очевидно гармонической, то очевидно удобство разложения любой гармонической (да и не только гармонической) волны по плоским гармоническим волнам. В каких-то случаях и в какой-то мере это может быть полезным и в случаях неоднородности пространства, хотя в этом случае это вполне может и не дать ожидаемых преимуществ, или извлечение этих преимуществ может потребовать особого искусства.
Сферические гармонические волны
Сферические гармонические волны несколько менее универсальны и просты (их гораздо труднее даже выписать в явном виде, если не выражать просто через бесконечные суммы/интегралы плоских волн; например, для двумерного пространства гармонические сферические волны выражаются через функции Бесселя, то есть не выражаются через элементарные функции).
Тем не менее они бывают очень полезны, когда сами условия задачи склоняют к попытке рассмотрения сферических волн, то есть, в особенности при исследовании волн, порождаемых точечным источником или когда задача в целом имеет сферическую симметрию (последнее лучше всего для попытки искать решение просто в виде только сферических волн).
Для трехмерного однородного пространства гармонические сферические волны имеют вид:
или (в виде, удобном в качестве для разложения):
Значение и теоретическое применение
Общий линейный случай
Любое линейное дифференциальное уравнение вида
Действительно, подставим 
, где x — точка пространства любой размерности. Получаем тогда:
а экспонента сокращается. Сделав такую же подстановку с -ω, получим, при оговоренных выше условиях подходящего K, получить и действительное v как сумму этих двух решений.
Примечания
См. также
Полезное
Смотреть что такое «Гармоническая волна» в других словарях:
гармоническая волна — Волна, при которой все точки среды совершают гармонические колебания. [ГОСТ 24346 80] Тематики вибрация EN harmonic wave DE harmonische welle FR onde harmonique … Справочник технического переводчика
Гармоническая волна — 66. Гармоническая волна Волна, при которой все точки среды совершают гармонические колебания Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации
гармоническая волна — harmoninė banga statusas T sritis fizika atitikmenys: angl. harmonic wave vok. harmonische Welle, f rus. гармоническая волна, f pranc. onde harmonique, f … Fizikos terminų žodynas
незатухающая гармоническая волна — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN continuous wave … Справочник технического переводчика
Волна — У этого термина существуют и другие значения, см. Волна (значения). Волна изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами,… … Википедия
Волна — процесс распространения изменений в состоянии среды (в частности, колебательного характера), при котором происходит перенос энергии без переноса вещества. Идеальная волна гармоническая, изменяющаяся по синусоидальному закону … Начала современного естествознания
Монохроматическая волна — Монохроматическая волна модель в физике, удобная для теоретического описания явлений волновой природы, означающая, что в спектр волны входит всего одна составляющая по частоте. Содержание 1 Основные свойства … Википедия
СФЕРИЧЕСКАЯ ВОЛНА — волна, радиально расходящаяся от источника или сходящаяся к приёмнику; волн. фронт её сфера. Простейшим примером явл. гармонич. симметричная С. в. в среде без поглощения: где r расстояние от источника, А/r амплитуда, w±kr фаза волны, w круговая… … Физическая энциклопедия
Волны — Волна изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию. Другими словами: «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой… … Википедия
ГОСТ 24346-80: Вибрация. Термины и определения — Терминология ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа: 112. Автоколебания Колебания системы, возникающие в результате самовозбуждения Определения термина из разных документов: Автоколебания 137. Активная виброзащита… … Словарь-справочник терминов нормативно-технической документации
Физика Б1.Б8.
Электронное учебное пособие по разделу курса физики Механика
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
Введение
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.
Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).
Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отброс ить несущественные, усложняющие решение.
Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.
Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.
Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.
Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.
★ Гармоническая волна
В разных случаях, если необходимо подчеркнуть интересный класс гармонических волн, например, плоская гармоническая волна, стоячая гармоническая волна и т. д. см. ниже.
Источниками гармонических волн могут быть гармонические колебания, они также могут быть возбуждены в любой системе при ее взаимодействии с гармонической волной.
1. В одномерном случае. (In the one-dimensional case)
В данном случае, все типы гармонических волн сводятся к:
а также конечных линейных комбинаций волн этого типа для выражения произвольных реальных гармонических волн в этом случае достаточно смешать две волны первого типа или второго четыре, в случае высших измерений u добавляет два таких терминов для каждой поляризации.
u x (у), t = A e i k x (Т = А Е и к) − ω t = | A | e i A r g A e i k x (е я а р г е и к) − ω t = | A | e i k x (е и к) − ω t + A r g A (А р г). <\displaystyle ux,t=A\ e^
Так же, как стоячей волны выражается как в двух, так что бег может быть выражена через две стоят. так что вы можете выбрать один из двух равноправных способов выражения произвольной гармонической волны в случае одномерных однородных пространств: с помощью линейной комбинацией беговой дорожке или линейной комбинации стоячих волн. это справедливо и для всех остальных случаях, хотя основные волны, используя линейную комбинацию, которая выражает произвольная гармоническая волна может быть сложнее.
2. В случае размерности пространства большей, чем одна. (In the case of space dimension greater than one)
В случае размерности пространства большей, чем одна, даже если она однородна, в принципе разнообразие возможных гармонических волн очень однако много. больше, есть два типа гармонических волн, которые должны уделять больше индивидуального внимания.
2.1. В случае размерности пространства большей, чем одна. Плоских гармонических волн. (Plane harmonic waves)
Самый важный и распространенный тип гармонические волны плоские гармонические волны в одномерной гармонической волны одномерные особый случай.
u x (у), t = A e i k (Т = А Е и) → ⋅ x → − ω t, <\displaystyle ux,t=A\ e^
Точно так же, как в одномерном случае, постоянного и бегущей гармонической волны той же частоты, с тем же может быть, с точностью до знака волнового вектора элементарных линейно выражаются друг через друга.
Поскольку преобразование Фурье практически любую функцию пространственных координат можно представить в виде суммы интеграла функции, представляющие собой плоскую волну, а зависимость от времени, тогда, для случая однородных пространств проявляется также гармоники, то, очевидно, любой гармоники разложения и не только гармонических волн на плоских гармонических волн. В некоторых случаях и в некоторой степени это может быть полезно в случаях неоднородности пространства, хотя в этом случае она может не дать ожидаемых преимуществ, или извлекать эти преимущества требуют особого искусства.
2.2. В случае размерности пространства большей, чем одна. Сферические гармонические волны. (Spherical harmonic waves)
Сферическая гармоническая волна является несколько менее универсален и прост.
Однако, они могут быть очень полезно, когда условия задачи склонны пытаться рассматривать сферических волн, т. е., в частности, в исследовании волн, генерируемых точечным источником, или когда задача в целом имеет сферическую симметрию последнее лучше всего, чтобы попытаться найти решение только в виде сферических волн.
Для трехмерных однородных пространств сферической гармонических волн имеют вид:
или в форме, пригодной как для разложения:
u r (у), t = A c o s k r (т = д п О С К) ⋅ c o s (П О) ω t r (т) <\displaystyle ur,t=A\ <\frac
3. Значение и теоретическое применение. (Value and theoretical application)
В линейном случае общие. (In the linear case, the total)
Любое линейное дифференциальное уравнение вида
где того времени дифференцирования n может быть любым самое интересное n = 1 (Н = 1) или 2, и L любой линейный дифференциальный оператор, который не зависит от t будет иметь решение гармонической волны.
1.3 Гармоническая волна и ее параметры
Гармоническая волна – волна, изменяющаяся во времени по гармоническому (синусоидальному) закону. Для этой волны также употребляется термин монохроматическая (одноцветная) волна, заимствованный из оптики. Любой волновой процесс можно представить с помощью преобразований Фурье через гармонические волны.
Кратко остановимся на основных определениях и понятиях гармонической волны. Уравнения плоской гармонической волны, распространяющейся, например, вдоль оси zв среде без потерь записывается в следующем виде
(1.1)
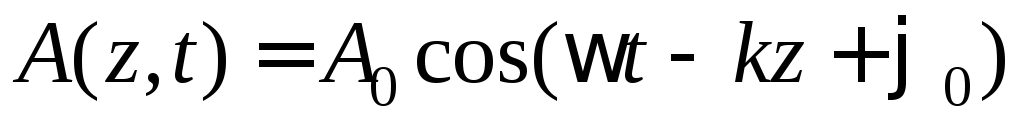
Под величиной A понимается физическая величина, определяющая волновой процесс. Максимальное значение этой величины называется амплитудой, обозначенной в (1.1) через
. Размерность амплитуды определяется природой волнового процесса. Например, в звуковых волнах амплитуда измеряется в единицах давления паскалях (Па), в электромагнитных волнах амплитуда напряженности электрического поля измеряется в вольтах на метр (В/м), а магнитного поля – в амперах на метр (А/м).
Выражение, стоящее в скобках (1.1), называется фазой колебания, через которую определяется значение физической величины в данный момент времени и в данной точке пространства. Константа j0называется начальной фазой, использование которой имеет смысл при сравнении двух и более волн одной частоты в данной точке пространства и в фиксированный момент времени. Круговая частотаwсвязана с частотойf(число колебаний в единицу времени) соотношением
(1.2)
Частота wизмеряется в радианах в секунду, частотаfв герцах (1Гц – одно колебание в секунду). При известной частотеf период колебания находится из соотношения
. (1.3)
Из периодичности волнового процесса в пространстве определяется длина волны
. (1.4)
Таким образом, длина волны – пространственный интервал, по прохождению которого фаза волны меняется на 
вдоль направления распространения. Число длин волн, укладывающихся на расстоянии
метров, называется волновым числом и обозначаетсяk.
Поверхность, на которой волновой процесс имеет одинаковую фазу колебания, называется поверхностью равных фаз или фронтом волны. По форме фронта волны можно выделить плоские, цилиндрические и сферические волны. Поверхность, на которой амплитуда волнового процесса постоянна, называется поверхностью равных амплитуд. Волна называется однородной, если у нее поверхности равных амплитуд и равных фаз совпадают, то есть на поверхности фронта не меняется амплитуда волнового процесса. В неоднородной волне амплитуда на поверхности фронта изменяется.
Плотность потока энергии (или интенсивность) волны – это энергия, переносимая волной через единицу перпендикулярно ориентированной поверхности за единицу времени. Плотность потока энергии пропорциональна квадратуре амплитуды волны
, (1.5)
где p– коэффициент пропорциональности, зависящий от свойств среды и типа волны;
– единичный вектор, показывающий направление распространения энергии.
Вектор плотности потока энергии в единицу времени (плотности потока мощности) принято называть вектором Умова-Пойнтинга.
Распространение волны происходит в направлении, перпендикулярном поверхности фронта волны. Плоская волна идет в одном направлении по нормали к ее фронту. Цилиндрическая волна расходится по радиусу в плоскости, перпендикулярной оси цилиндра. Сферическая волна расходится по радиусу перпендикулярно сферическому фронту. Элемент поверхности цилиндрического фронта 
возрастает прямо пропорционально расстоянию, при этом плотность потока мощности убывает обратно пропорционально расстоянию, а амплитуда цилиндрической волны убывает обратно пропорционально корню квадратному из расстояния. Элемент поверхности сферического фронта
возрастает пропорционально квадрату расстояния, плотность потока мощности уменьшается обратно пропорционально квадрату расстояния, а амплитуда сферической волны убывает обратно пропорционально расстоянию. В среде с потерями распространяющиеся волны теряют часть своей энергии и их амплитуды убывают по экспоненциальному закону вдоль направления распространения.