что такое двойственная функция

Что такое двойственная функция

Определение. Булева функция f * (x₁, …, x_n) называется двойственной булевой функции f(x₁, …, x_n), если она получена из f(x₁, …, x_n) инверсией всех аргументов и самой функции, то есть

Пример. Построим функцию, двойственную стрелке Пирса.

Пусть булева функция f(x₁, …, x_n) задана формулой F_f. Чтобы получить формулу F’_{f *} для функции f * (x₁, …, x_n), двойственной функции f(x₁, …, x_n), необходимо, согласно определению, проинвертировать все переменные, пользуясь при этом законом двойного отрицания, и саму функцию. При этом формулу F’_{f *} можно упростить (убрать длинную инверсию над формулой), заменив символ функции, которая вычисляется последней, на символ инверсной ей функции.

Пример. Пусть F_f = x ↓ (y ( x y z) ) ( y x ). Последней должна вычислятьси импликация, инверсная ей функция это обратная импликация, поэтому формула для двойственной функции примет вид:

Алгоритм построения таблицы истинности двойственной функции (основан на определении двойственной функции).

Инверсия всех переменных превращает наборы в их антиподы. Поскольку в таблице истинности антипод первого набора расположен последним, антипод второго набора – предпоследним и так далее, то для построения функции f( x ₁, …, x _n) нужно перевернуть вектор-столбец значений исходной функции f(x₁, …, x_n), а для получения функции f ( x ₁, …, x _n) еще и инвертировать компоненты столбца.

Пример. Построим функцию, двойственную стрелке Пирса.

Пары двойственных элементарных функций:

Тождественная функция и инверсия двойственны каждая самой себе.

Для доказательства можно воспользоваться алгоритмом построения таблицы истинности двойственной функции (именно так предыдущий пример демонстрирует, что штрих Шеффера двойственен стрелке Пирса), или применить равносильные преобразования.

Пример. Покажем, что дизъюнкция двойственна конъюнкции (применив законы де Моргана и двойного отрицания):

Источник

Презентация по математической логике на тему «Двойственные функции»

Описание презентации по отдельным слайдам:

Двойственные функции Булевы функции

Двойственные функции Булева функция f*(x1, …, xn) называется двойственной булевой функции f(x1, …, xn), если она получена из f(x1, …, xn) инверсией всех аргументов и самой функции, то есть

Пример Построим функцию, двойственную стрелке Пирса. Значения двойственной функции можно получить переворотом и инверсией столбца значений исходной функции

Пример. Покажем, что дизъюнкция двойственна конъюнкции (применив законы де Моргана и двойного отрицания):

Двойственная формула Определение Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций. Пример

Пример Рассмотрим формулу задающую булеву функцию НЕ-ИЛИ, то есть стрелку Пирса. Двойственная ей формула должна задавать функцию, двойственную стрелке Пирса – это штрих Шеффера: в самом деле это функция НЕ-И, то есть штрих Шеффера.

Самодвойственная функция Функция, совпадающая со своей двойственной, называется самодвойственной. F*=F Следствие из принципа двойственности. Если формулы F1 и F2 равносильны, то двойственные им формулы F*1 и F*2, также равносильны.

Способы получения двойственной функции – по определению двойственной функции – инверсией в формуле Ff всех аргументов и самой функции; – по определению двойственной формулы и принципу двойственности – заменой в формуле Ff символов функций на символы двойственных им функций; – построением таблицы истинности исходной функции по заданной формуле Ff, а затем переходом к таблице истинности двойственной функции (переворотом и инверсией столбца значений исходной функции).

Упражнение 1 Построить формулы для функций, двойственных данным, пользуясь двумя разными способами: определением двойственной функции и принципом двойственности. Сравнить таблицы истинности, построенные по полученным формулам.

Упражнение 2 Двойственны ли формулы Ff и Gg? Функции f и g?

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-011113

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В Госдуме предлагают сделать бесплатным проезд на общественном транспорте для детей до 16 лет

Время чтения: 2 минуты

В проекте КоАП отказались от штрафов для школ

Время чтения: 2 минуты

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Вопрос о QR-кодах для сотрудников школ пока не обсуждается

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Что такое двойственная функция

Определение. Формула F * называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций.

F = x ↓ (y ( x y z) ) ( y x ),

F * = x / (y x (y z)) ( y x ). •

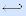
Теорема (принцип двойственности). Если формула F задает булеву функцию f(x₁, …, x_n), то двойственная ей формула F * задает двойственную функцию f * (x₁, …, x_n).

Доказательство. По условию теоремы формула F задает булеву функцию f(x₁, …, x_n). По определению формулы F имеем:

Рассмотрим двойственную ей формулу:

[ по определению двойственной функции для f_i * (x₁, …, x_n), i=1, …, m ]

[ по определению двойственной функции для f₀ * (y₁, …, y_m) ]

[ по закону двойного отрицания ]

[ по определению двойственной функции для f(x₁, …, x_n ]

Пример. Рассмотрим формулу F = 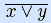, задающую булеву функцию НЕ-ИЛИ, то есть стрелку Пирса. Двойственная ей формула F * = x y должна задавать функцию, двойственную стрелке Пирса – это штрих Шеффера: в самом деле F * = x y – это функция НЕ-И, то есть штрих Шеффера. •

Следствие из принципа двойственности. Если формулы F₁ и F₂ равносильны, то двойственные им формулы F * ₁ и F * ₂, также равносильны.

Доказательство. Равносильные формулы F₁ и F₂задают одну и ту же булеву функцию f(x₁, …, x_n), следовательно, по принципу двойственности, двойственные им формулы F * ₁ и F * ₂, задают двойственную f(x₁, …, x_n) функцию f * (x₁, …, x_n). •

Таким образом, можно не доказывать некоторые равносильности (в том числе и основные), а выводить их, пользуясь следствием из принципа двойственности.

Источник

Двойственная задача линейного программирования

Двойственная задача линейного программирования

Теорема двойственности

Важнейшие свойства пары двойственных задач математического программирования сформулированы в трех основных теоремах.

Теорема двойственности

Допустимый вектор решения прямой задачи программирования оптимален тогда и только тогда, когда существует такой допустимый вектор решения двойственной задачи, что целевые функции прямой и двойственной задачи равны. Допустимый вектор двойственной задачи оптимален тогда и только тогда, когда существует допустимый вектор прямой задачи и целевые функции обеих задач равны.

Теорема существования решения

Если существуют допустимые векторы решений прямой и двойственной задач, то обе задачи имеют оптимальные векторы. Если одна из двух задач не имеет допустимого вектора, то ни одна из них не имеет оптимального вектора решения.

Теорема (принцип) дополняющей нежесткости

Оптимальное решение прямой задачи программирования получается только при одном значении x_Q. Это справедливо и для переменной y_Q в двойственной задаче.

Теоремы двойственности

Основное неравенство двойственности. Для любых допустимых решений Х и Y пары двойственных ЗЛП имеет место неравенство

Экономически это означает, что для любого допустимого плана производства и любого дополнительного вектора оценок ресурсов (на складе) стоимость изготовленного продукта не превосходит оценки ресурсов.

Теорема существования (малая тероема двойственности)

Чтобы прямая и двойственная задачи имели opt решения, необходимо и достаточно, чтобы существовали допустимые решения для каждой из них.

Теорема 1 двойственности.

Если одна из пары двойственных задач имеет opt решение, то и другая его имеет. Причем экспериментальные решения их целевых ф. равны; если же ЦФ одной из задач не ограничена, то система ограничений другой противоречива. Интерпретация: оптимальное использование ресурсов – opt план. Суммарная оценка ресурсов = оценке продукта полученного при opt плане. Любой другой план не рентабелен. C_j – стоимость единицы продукции (внешняя оценка) y_i – стоимость единицы ресурса (внутренняя оценка). Эти двойственные оценки выступают как инструменты балансирования затрат и результатов. Имеет место x_j ​ ​ y_m +_j ; x_n+i y_i.

Теорема 2 двойственности (о дополняющей нежесткости)

Для того, чтобы допустимые решения X и Y пары двойственных задач были оптимальными, необходимо и достаточно выполнить условия:

То есть, если какое-либо ограничение одной ЗЛП обращается ее opt планом в строгое равенство, то соответствующая переменная двойственной задачи в ее opt плане равна нулю; если же какая-либо переменная opt-го решения одной ЗЛП положительна, то соответствующее ограничение в двойственной ЗЛП ее opt планом обращается в точное равенство.

Теорема Кёнига хорошо иллюстрирует использование принципа двойственности ЗЛП.

Формулирование теоремы. Максимальное число попарно неколлинеарных единиц любой булевой матрицы равно минимальному числу линий, покрывающих все единицы матрицы.

Доказательство. Для нахождения максимального числа попарно неколлинеарных единиц булевой матрицы достаточно сформулировать и решить линейную задачу:

Минимальное число линий, покрывающих все единицы матрицы [C_ij], найдем, решив линейную задачу:

Оптимальному решению (u*_i, v*_j) последней задачи отвечает минимальное покрытие, состоящее из множества строк I, для которых u*_i = 1 и столбцов J, для которых u*_j =1.

Матрицы А и А Т коэффициентов (*), (**), (***) являются абсолютно унимодулярными, как матрицы двудольного графа. Поэтому условия целочисленности переменных заменяем на условие их неотрицательности, и тогда получаем пару двойственных задач линейного программирования и согласно теореме двойственности имеем:

Линией матрицы называется ее строка или столбец. Два элемента матрицы называются неколлинеарными, если они не лежат на одной линии.

Матрица называется абсолютно унимодулярной, если все ее ненулевые миноры равны 1, либо -1.

Следствие. Матрица инциденций неориентированного графа G абсолютно унимодулярна тогда и только тогда, когда G – двудольный граф. В двудольном графе все простые циклы имеют четкую длину

Принцип двойственности в задачах линейного программирования.

Предположим, что руководство предприятия из анализа конъюнктуры рынка продукции приняли решение: производство сократить, а от запасов сырья избавиться, (продать на рынке) и при этом не нанести себе убытков.

С этой целью руководство должно назначить стоимости y_i за единицу сырья вида S_i, стремясь при этом минимизировать общую стоимость сырья (чтобы быстрее продать сырье): Ф = Σ 4 _i=1 b_iy_i

Выручка предприятия от продажи сырья, расходуемого на единицу продукции П_i, составит: Σ 4 _i=1 a_ij y_i

И по условию она не должна быть меньше С_j (в противном случае предприятию выгоднее не продавать сырье, а использовать его для нужд производства, выпуска продукции).

Сформулируем исходную и двойственную задачи:

Обе задачи по отношению друг к другу называются двойственными или сопряженными. Анализ таблицы позволяет сделать выводы:

Если первая задача сформулирована на поиск максимума, то вторая формулируется на поиск минимума линейной функции.

Коэффициенты ЦФ первой задачи являются свободными членами системы ограничений второй.

Свободные члены системы ограничений первой задачи являются коэффициентами линейной системы во второй задаче.

Матрица коэффициентов второй задачи является транспонированной к матрице коэффициентов ограничений первой задачи.

Знаки неравенств в ограничениях второй задачи противоположны знакам неравенств в ограничениях первой задачи.

Для того чтобы векторы X opt = и Y opt = были решениями пары задач, необходимо и достаточно, чтобы их компоненты удовлетворяли следующим условиям:

Эти условия называют принципом дополняющей нежесткости. Если исходная (прямая) задача задана в канонической форме, то двойственная к ней называется несимметричной. Для несимметричной двойственной задачи соблюдается условие y_i ≥ 0.

Теория ЗЛП доказывает, что компоненты оптимальных планов взаимно двойственных задач, приведенных к каноническому виду, соответствуют одни другим. То есть базисные переменные основной задачи соответствуют свободным переменным двойственной задачи и наоборот, j = 1(1)n, x*_j ​ y*_{m +j} ; x*_n+i ​ y*_i ; i = 1(1)m.

Размерности в табличке m и n берутся в задаче для y-ков записанной в канонической форме.

Пример. Двойственный симплекс метод.

Исходная задача. Имеется три вида продуктов П_j, причем единица веса каждого из видов продуктов содержит a_ij единиц (питательных веществ). Для нормальной жизнедеятельности человек должен потреблять не менее b_i единиц вещества B_i в сутки. Стоимость единицы продукта П_j равняется C_j. Требуется составить оптимальный суточный рацион питания, т.е. найти количество x_j продукта, которое должен потреблять человек, чтобы стоимость питания была бы минимальной, если известно, что

такие значения его компонентов x_j, j = 1(1)3, которые минимизируют целевую функцию (Ц) Q = 3x₁ + 2x₂ + x₃ и удовлетворяют ограничениям неравенствам

x_j ≥ 0; j = 1(1)3 = n

Для приведения задачи к каноническому виду введем дополнительные переменные x₄, x₅, x₆, x₇, переменных стало больше чем уравнений n – m = 7 – 4 = 3, следовательно, части из них (трем любым,) для получения решения можно задать произвольные значения (задают, как правило, нулевые значения), возникает число сочетаний из n по m вариантов. Система ограничений примет вид равенств

x_j ≥ 0; j = 1(1)3 = n, i = 1(1)4 = m.

Назначаем опорный план. Выбор в качестве базисных переменных x₄, x₅, x₆, x₇ приводит к недопустимому опорному плану. Так как знаки левой и правой частей различны. (Свободные переменные x₁ = x₂ = x₃ = 0) Метод искусственного базиса приводит к увеличению числа неизвестных задач, что нежелательно. Анализ задачи показывает, что число уравнений в системе ограничений больше числа переменных. Поэтому попытаемся применить принцип двойственности, т.е. вначале решим двойственную ЗЛП, а затем найдем решение исходной.

y_i ≥ 0; i = 1(1)4.

при ограничениях (в ограничения добавили новые переменные):

y_i ≥ 0; i = 1(1)7.

Базисные переменные y₅, y₆, y₇ и ЦФ выражаем через свободные переменные, т.е. из свободных членов (правых частей, обозначенных γ_i ) вычитаем левые части ограничений

γ₀ =0, так как ЦФ не содержит свободного члена.

и строим симплекс таблицу с двумя полуклетками. Направляющий столбец y₃, направляющая строка y₆.

Анализ таблицы показывает, что все коэффициенты ЦФ при свободных переменных положительны. Следовательно, план Y не является оптимальным, ЦФ можно уменьшить, увеличивая значения соответствующих свободных переменных.

Находим γ = max<γ_i> =max <0,2; 0,5; 0,6; 0,1>= 0,6. Переменную y₃ надо ввести в базис. После этого устанавливаем, существует ли оптимальный план. В направляющем столбце все коэффициенты положительны, следовательно, оптимальный план существует. В базисе есть переменные, которые можно уменьшать до нуля увеличивая значения y₃, тем самым минимизируя ЦФ. Раньше других в нуль обратиться переменная y₆ и ее исключаем из базиса.

После замены переменных в базисе переходим к новой симплексной таблице.

Ваулин А. Е. Методы цифровой обработки данных.– СПб.: ВИККИ им. А. Ф. Можайского, 1993.– 106 с.

Гэри М., Джонсон Д. Вычислительные машины и трудно решаемые задачи. М.: Мир, 1982.

Корбут А.А., Финкельштейн Ю. Ю. Дискретное программирование М. Наука. Гл. ред. физ.-мат. лит. 1969.

Макаров И. М. и др. Теория выбора и принятия решений.– М.: Наука, 1982.– 328 с.

Пфанцагль И. Теория измерений. – М.: Наука, 1988.–384 с.

Таха Х. А. Введение в исследование операций. 7-е изд. М.: Изд. дом «Вильямс», 2005.

Фишберн П. С. Теория полезности для принятия решений. – М.: Наука,1978. –352 с.

Источник