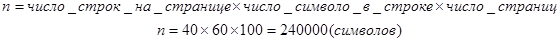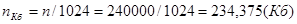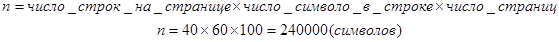что такое двоичный алфавит
5rik.ru
Материалы для учебы и работы
Двоичный алфавит.
В информатике и вычислительной технике широко используется алфавит, имеющий два знака, например «1» и «0». Этими символами в логике и технике приводят в соответствие понятия «да» и «нет», «есть сигнал» и «нет сигнала», «истина» и «ложь». Такой алфавит называют двоичным или бинарным (binary) в соответствии с этим вводится наименьшая единица информации бит (bit).
В реальной жизни крайне редко встречаются объекты состояние которых можно закодировать одним битом информации и нет объектов, которые можно описать одним битом. Для кодирования от трех до четырех состояний или признаков объекта требуется уже два бита информации. Для кодирования от четырех до девяти состояний объекта уже требуется три бита. 9-16 состояний 4 бита, 17-32 состояний 5 бит. В общем случае количество бит, необходимых для кодирования N состояний или диапазона значений свойств объектов или явлений определяется по формуле 1:
 | (1) |
N – количество состояний или диапазон значений свойств объектов,
q – количество бит информации необходимых для кодирования требуемого количества состояний или диапазона свойств объектов.
Было принято, что следующей базовой единицей информации будет являться байт – это последовательность бит длина которой равна 8 битам. Одним байтом можно закодировать от 1 до 256 различных объектов, например символов.
На практике используются более объемные единицы измерения информации, приведенные в таблице 1.
| 1 байт | =8 бит |
| 1 слово | =2 байта = 16 бит |
| 1 двойное с слово | =2 слова = 4 байта=32 бита |
| 1 килобайт (Кб) | =1024 байт  |
| 1 мегабайт (Мб) | =1024 килобайт =  |
| 1 гигабайт (Гб) | =1024 мегабайт =  |
| 1 терабайт (Тб) | =1024 гигабайт =  |
Пример 1.
Подсчитаем объем памяти, требуемый для хранения книги объемом 100 страниц, при учете, что в среднем на каждой странице по 40 строк, а в каждой строке в среднем по 60 символов.
ü Определяем количество символов находящихся в книге:
ü При условии, что символ занимает 1 байт памяти для хранения книги потребуется 240000 байт памяти или
Двоичная система счисления
Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.
Немного истории
Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.
Таблица и алфавит
Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.
1001102 = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 3810
Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:
| Делимое | 38 | 19 | 9 | 4 | 2 |
|---|---|---|---|---|---|
| Делитель | 2 | 2 | 2 | 2 | 2 |
| Частное | 19 | 9 | 4 | 2 | 1 |
| Остаток | 0 | 1 | 1 | 0 | 0 |
Для перевода в другие системы необходимо:
Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:
| Двоичная | Восьмеричная | Шестнадцатеричная |
|---|---|---|
| 0 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | |
| 1001 | 9 | |
| 1010 | A | |
| 1011 | B | |
| 1100 | C | |
| 1101 | D | |
| 1110 | E | |
| 1111 | F |
110010012 = 11 001 001 = 011 001 001 = 3118
110010012 = 1100 1001 = С916
Представление двоичных чисел
В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.
Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.
Прямой код предполагает приписывание единицы в начале без изменений записи:
| A > 0 | Aпр = 0A | 1010112; Aпр = 01010112 |
| A ≤ 0 | Aпр = 1|A| | -1010112; Aпр = 11010112 |
Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:
| A > 0 | Aобр = 0A | 1010112; Aобр = 01010112 |
| A ≤ 0 | Aобр = 1 A | -1010112; Aобр = 10101002 |
Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:
| A > 0 | Aдоп = 0A | 1010112; Aдоп = 01010112 |
| A ≤ 0 | Aдоп = 1 A + 1 | -1010112; Aдоп = 10101012 |
Применение двоичной системы в информатике
Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.
Двоичный алфавит
В информатике и вычислительной технике широко используется алфавит, имеющий два знака, например «1» и «0». Этими символами в логике и технике приводят в соответствие понятия «да» и «нет», «есть сигнал» и «нет сигнала», «истина» и «ложь». Такой алфавит называют двоичным или бинарным (binary) в соответствии с этим вводится наименьшая единица информации бит (bit).
В реальной жизни крайне редко встречаются объекты состояние которых можно закодировать одним битом информации и нет объектов, которые можно описать одним битом. Для кодирования от трех до четырех состояний или признаков объекта требуется уже два бита информации. Для кодирования от четырех до девяти состояний объекта уже требуется три бита. 9-16 состояний 4 бита, 17-32 состояний 5 бит. В общем случае количество бит, необходимых для кодирования N состояний или диапазона значений свойств объектов или явлений определяется по формуле 1:
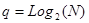 | (1) |
N – количество состояний или диапазон значений свойств объектов,
q – количество бит информации необходимых для кодирования требуемого количества состояний или диапазона свойств объектов.
Было принято, что следующей базовой единицей информации будет являться байт – это последовательность бит длина которой равна 8 битам. Одним байтом можно закодировать от 1 до 256 различных объектов, например символов.
На практике используются более объемные единицы измерения информации, приведенные в таблице 1.
| 1 байт | =8 бит |
| 1 слово | =2 байта = 16 бит |
| 1 двойное с слово | =2 слова = 4 байта=32 бита |
| 1 килобайт (Кб) | =1024 байт 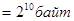 |
| 1 мегабайт (Мб) | =1024 килобайт = 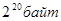 |
| 1 гигабайт (Гб) | =1024 мегабайт = 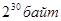 |
| 1 терабайт (Тб) | =1024 гигабайт = 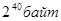 |
Пример 1.
Подсчитаем объем памяти, требуемый для хранения книги объемом 100 страниц, при учете, что в среднем на каждой странице по 40 строк, а в каждой строке в среднем по 60 символов.
ü Определяем количество символов находящихся в книге:
ü При условии, что символ занимает 1 байт памяти для хранения книги потребуется 240000 байт памяти или
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Двоичный алфавит



В информатике и вычислительной технике широко используется алфавит, имеющий два знака, например «1» и «0». Этими символами в логике и технике приводят в соответствие понятия «да» и «нет», «есть сигнал» и «нет сигнала», «истина» и «ложь». Такой алфавит называют двоичным или бинарным (binary) в соответствии с этим вводится наименьшая единица информации бит (bit).
В реальной жизни крайне редко встречаются объекты состояние которых можно закодировать одним битом информации и нет объектов, которые можно описать одним битом. Для кодирования от трех до четырех состояний или признаков объекта требуется уже два бита информации. Для кодирования от четырех до девяти состояний объекта уже требуется три бита. 9-16 состояний 4 бита, 17-32 состояний 5 бит. В общем случае количество бит, необходимых для кодирования N состояний или диапазона значений свойств объектов или явлений определяется по формуле 1:
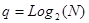 | (1) |
N – количество состояний или диапазон значений свойств объектов,
q – количество бит информации необходимых для кодирования требуемого количества состояний или диапазона свойств объектов.
Было принято, что следующей базовой единицей информации будет являться байт – это последовательность бит длина которой равна 8 битам. Одним байтом можно закодировать от 1 до 256 различных объектов, например символов.
На практике используются более объемные единицы измерения информации, приведенные в таблице 1.
| 1 байт | =8 бит |
| 1 слово | =2 байта = 16 бит |
| 1 двойное с слово | =2 слова = 4 байта=32 бита |
| 1 килобайт (Кб) | =1024 байт 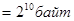 |
| 1 мегабайт (Мб) | =1024 килобайт = 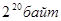 |
| 1 гигабайт (Гб) | =1024 мегабайт = 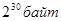 |
| 1 терабайт (Тб) | =1024 гигабайт = 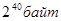 |
Пример 1.
Подсчитаем объем памяти, требуемый для хранения книги объемом 100 страниц, при учете, что в среднем на каждой странице по 40 строк, а в каждой строке в среднем по 60 символов.
ü Определяем количество символов находящихся в книге:
ü При условии, что символ занимает 1 байт памяти для хранения книги потребуется 240000 байт памяти или
Информатика. 7 класс
Конспект урока
Кодирование информации. Двоичный код
Перечень вопросов, рассматриваемых в теме:
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную. Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
Алфавит языка – конечный набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита – это количество входящих в него символов.
Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием. Двоичное кодирование универсально, так как с его помощью может быть представлена любая информация.
1. Босова Л. Л. Информатика: 7 класс. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2017. – 226 с.
Теоретический материал для самостоятельного изучения
Для решения своих задач человеку часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух происходит преобразование информации из дискретной (текстовой) формы в непрерывную (звук). Во время диктанта на уроке русского языка, наоборот, происходит преобразование информации из непрерывной формы (голос учителя) в дискретную (записи учеников).
Информация, представленная в дискретной форме, значительно проще для передачи, хранения или автоматической обработки. Поэтому в компьютерной технике большое внимание уделяется методам преобразования информации из непрерывной формы в дискретную.
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную.
Рассмотрим суть процесса дискретизации информации на примере.
На метеорологических станциях имеются самопишущие приборы для непрерывной записи атмосферного давления. Результатом их работы являются барограммы – кривые, показывающие, как изменялось давление в течение длительных промежутков времени. Одна из таких кривых, вычерченная прибором в течение семи часов проведения наблюдений, показана на рисунке 1.
На основании полученной информации можно построить таблицу, содержащую показания прибора в начале измерений и на конец каждого часа наблюдений.
Полученная таблица даёт не совсем полную картину того, как изменялось давление за время наблюдений: например, не указано самое большое значение давления, имевшее место в течение четвёртого часа наблюдений. Но если занести в таблицу значения давления, наблюдаемые каждые полчаса или 15 минут, то новая таблица будет давать более полное представление о том, как изменялось давление.
Таким образом, информацию, представленную в непрерывной форме (барограмму, кривую), мы с некоторой потерей точности преобразовали в дискретную форму (таблицу).
В дальнейшем вы познакомитесь со способами дискретного представления звуковой и графической информации.
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит – конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита – это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 3). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1. Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.
Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов. Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рисунке.
Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:
Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 – вдвое больше, чем из двух двоичных символов:
Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный – 32, шестиразрядный – 64 и т. д.
Длину двоичной цепочки – количество символов в двоичном коде – называют разрядностью двоичного кода.
Обратите внимание, что:
32 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 и т. д.
Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода – буквой i, то выявленная закономерность в общем виде будет записана так:
В математике такие произведения записывают в виде:
Запись 2 i читают так: «2 в i-й степени».
Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
Универсальность двоичного кодирования
В начале нашей беседы вы узнали, что информация, представленная в непрерывной форме, может быть выражена с помощью символов некоторого естественного или формального языка. В свою очередь, символы произвольного алфавита могут быть преобразованы в двоичный код. Таким образом, с помощью двоичного кода может быть представлена любая информация на естественных и формальных языках, а также изображения и звуки (рис. 6). Это и означает универсальность двоичного кодирования.
Двоичные коды широко используются в компьютерной технике, требуя только двух состояний электронной схемы – «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0).
Простота технической реализации – главное достоинство двоичного кодирования. Недостаток двоичного кодирования – большая длина получаемого кода.
Равномерные и неравномерные коды
Различают равномерные и неравномерные коды. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные – разное.
Выше мы рассмотрели равномерные двоичные коды.
Примером неравномерного кода может служить азбука Морзе, в которой для каждой буквы и цифры определена последовательность коротких и длинных сигналов. Так, букве Е соответствует короткий сигнал («точка»), а букве Ш – четыре длинных сигнала (четыре «тире»). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающиеся в передаваемой информации символы имеют самые короткие кодовые комбинации.
Разбор решения заданий тренировочного модуля
№1.Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Переведите десятичное число 273 в двоичную систему счисления.
Воспользуемся алгоритмом перевода целых чисел из системы с основанием p в систему с основанием q:
1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.
3. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Ответ: 27310= 100010001.
№2. Тип задания: единичный / множественный выбор.
Четыре буквы латинского алфавита закодированы кодами различной длины: