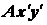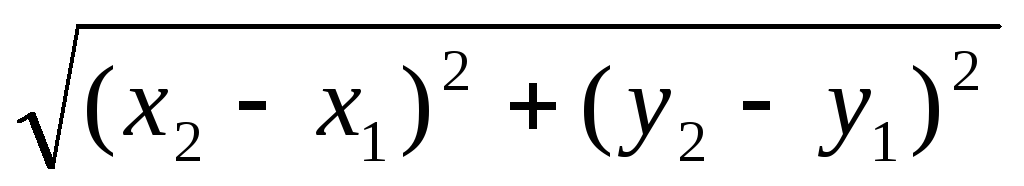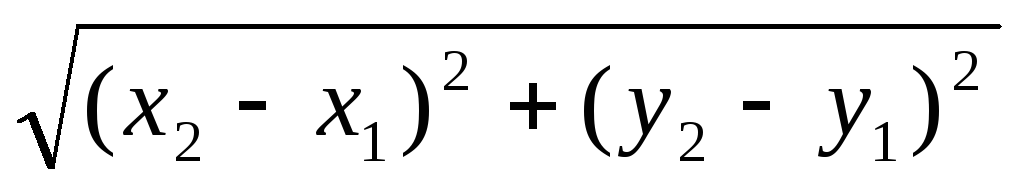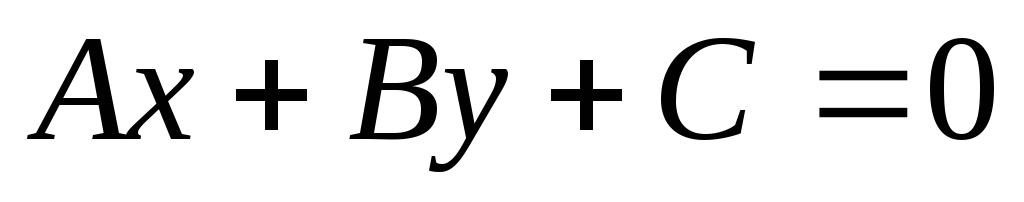что такое движение или перемещение плоскости

Движение тела на плоскости

В школьной физике в основном рассматривают движение тел вдоль прямой – одномерный случай. Реже — на плоскости, когда для описания координат используем две взаимно перпендикулярные оси «Ox» и «Oy», т. е. двумерный случай движения.

В случае поступательного движения на плоскости, мы раскладываем векторы перемещения, скорости и ускорения на проекции по осям. Каждую проекцию при этом можно рассматривать, как случай одномерного движения отдельного тела. Тогда для каждой оси имеется своя скорость, свое ускорение и свое перемещение этого тела.

Примечания:

Перемещение, скорость и ускорение на плоскости

Опишем движение материальной точки на плоскости. В процессе движения изменяются две координаты – «x» и «y». Перемещение тела для двумерного движения можно разделить на две проекции.

На рисунке 1 точка, в которой тело находилось в начале движения, имеет координаты \(\left( x_<0>; y_ <0>\right) \).

Конечная точка, в которую тело сместилось в процессе движения, имеет координаты \(\left( x; y \right) \).

Серая линия – это траектория тела, а вектор перемещения тела обозначен красным цветом.

Разложим вектор перемещения на проекции по осям:

\[ \large \begin S_ = x — x_ <0>\\ S_ = y — y_ <0>\end\]

А после запишем координаты вектора перемещения

Пользуясь известными проекциями на плоскости, мы можем посчитать модуль вектора перемещения:

\[ \large \left| \vec \right| = \sqrt < \left( S_\right)^2 + \left( S_ \right)^2> \]

На перемещение тела было затрачено время t. По известному перемещению мы можем найти скорости и ускорения тела.

Векторы скорости и ускорения тела на плоскости будут иметь две координаты

Физический смысл производной

Этот смысл применяется не только для движения на плоскости, а вообще, к любому движению.

Скорость – это первая производная вектора перемещения, взятая по времени

Запись читается, как «дэ эс по дэ тэ равно вэ».

Ускорение – это вторая производная вектора перемещения, взятая по времени

Эта запись читается, как «дэ два эс по дэ тэ дважды равно а».

Также, ускорение – это первая производная скорости по времени

Примечание: Словосочетание «физический смысл производной» следует понимать, как «что такое производная с точки зрения физики»

Перемещение самолета при боковом ветре

Найдем теперь перемещение тела, движущегося в горизонтальной плоскости.

Для решения задачи будем применять законы Ньютона, формулы кинематики и правила сложения векторов.

В горизонтальной плоскости летит самолет. Он движется по прямой с неизменной скоростью \(\vec>\), масса самолета \(m\). В некоторый момент времени подул ветер, перпендикулярно направлению, в котором движется самолет. Порыв ветра длился t секунд. Сила ветра, действующая на самолет, постоянная и равна \(\vec\). Найти координаты вектора конечной скорости самолета и перемещение самолета к тому моменту, когда ветер прекратился.

Решение задачи

Составим рисунок, на нем отметим векторы скорости самолета, силу воздействия на самолет и проведем оси. Координатные оси лежат в горизонтальной плоскости. Будем считать, что сила начала действовать на самолет в начальный момент времени \(t_ <0>= 0 \) секунд.

На рисунке 2 изображены векторы скорости самолета и силы воздействия бокового ветра.

Координаты вектора ускорения

В условии задачи написано, что на самолет действует боковая сила \(\vec\). Используем ее, чтобы записать силовое уравнение для оси Oy:

\[ \large F = m \cdot a_ \]

По второму закону Ньютона, когда ускорение есть, скорость тела будет изменяться. \(a_\) – это проекция ускорения, приобретенного самолетом, она сонаправлена с вектором силы. То есть, направлена вдоль оси Oy. Выразим это ускорение из силового уравнения:

По условию, вдоль оси Ox самолет движется с неизменной скоростью. Из первого закона Ньютона следует, что силы, действующие на самолет вдоль оси Ox, скомпенсированы. Значит, ускорения, направленного вдоль оси Ox, нет.

Таким образом, координаты вектора ускорения самолета будут иметь вид:

Координаты вектора скорости

Зная ускорение, мы можем составить уравнения для скорости тела.

В начальный момент времени скорость имеет такие координаты:

Вектор скорости изменится благодаря наличию вектора ускорения. В конечной точке траектории скорость будет иметь координаты, отличные от начальных:

Найдем координаты вектора конечной скорости. Конечная скорость будет больше начальной, значит, движение равноускоренное.

Запишем в векторном виде связь между начальной и конечной скоростью

Примечание: Складывать можно только векторы, которые измеряются в одинаковых единицах, другими словами, размерности которых совпадают! Мы можем Ньютоны складывать с Ньютонами, метры в секунду складывать с метрами в секунду и т. д.

Из рисунка видно, что вектор конечной скорости отклонился от первоначального направления на угол \( \alpha\). Направление вектора конечной скорости \( \vec \) совпадает с направлением вектора перемещения \( \vec \) самолета.

Координаты вектора конечной скорости — это сумма координат слагаемых векторов.

\[ \large \begin v_ = v_ <0x>+0 \\ v_ = 0 + a_ \cdot t \end\]

Окончательно запишем, вектор конечной скорости обладает такими координатами

\[ \large \vec = \left\ < v_<0x>; a_ \cdot t \right\> \]

Координаты вектора перемещения

Найдем теперь координаты вектора перемещения самолета. Графически траекторию движения самолета можно изобразить отрезком параболы, так, как это сделано на рисунке 4.

На рисунке 4 представлены траектория движения – кривая синяя линия и перемещение самолета – вектор AB, обозначенный красным цветом.

Координаты начальной точки A (0 ; 0).

Координаты конечной точки B \( \left( S_ ; S_ \right) \).

Точка, в которой находился самолет в момент, когда на него подействовала сила ветра, имела координаты (0 ; 0). Это значит, что в нашей задаче вектор перемещения является радиус вектором, его координаты совпадают с координатами его конечной точки B.

Скорость вдоль оси Ox не меняется \( \large v_= v_ <0x>\), поэтому вдоль этой оси движение равномерное.

Перемещение самолета для равномерного движения вдоль оси Ox запишем так

\[ \large S_ = v_ <0x>\cdot t \]

А вдоль оси Oy самолет из начальной точки равноускорено сместится на такую величину

\[ \large S_ = v_ <0y>\cdot t + a_ \cdot \frac> <2>\]

Пользуясь найденными координатами вектора перемещения, найдем его длину

\[ \large \left| \vec \right| = \sqrt < \left( S_\right)^2 + \left( S_ \right)^2> \]

Задача решена. Если будут известны числовые значения начальных данных, ответ можно будет выразить численно.

Источник

ГОСЫ / вопрос 3 / движение на плоскости

Движение. Виды движений. Классификация движений плоскости.

Группа движений плоскости и ее подгруппы.

Определение 15.1. Преобразование плоскости, сохраняющее расстояние, называется движением (перемещением).

Наиболее простейшим примером движения является тождественное преобразование плоскости на себя, при котором каждая её точка переходит в себя.

Определение 15.2. Репером называется упорядоченная тройка точек, не лежащих на одной прямой.

Репер является аффинным, если ΔАВС произвольный.

Репер называется ортонормированным, если ΔАВС – прямоугольный,

А=90º, AB=АС=1, А – начало репера, В и C – вершины репера.

Теорема 15.3. При движении репер R, образованный точками A, В, С, переходит в репер R`, образованный точками A`, B`, C`, причем это движение единственно и при этом движении точка М(x,y) переходит в точку М`(x,y).

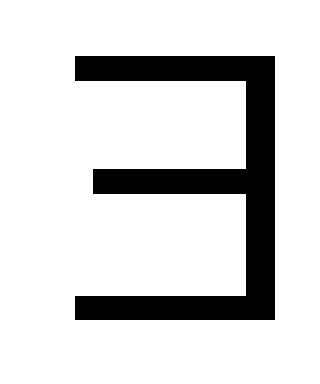
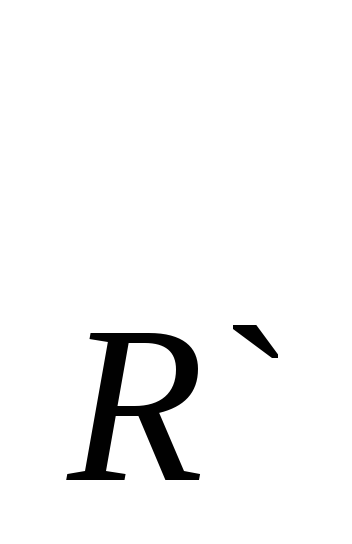
Докажем, что такое движение. Построим отображение плоскости на себя g: γ → γ такое, что R=(A, B, C) → R`=(A`, B`, C`) и М(x,y)→М`(x,y).

Реперы R и R` ортонормированные, тогда по построенному отображению имеем, что точка А(0,0)→А`(0,0), В(1,0)→В`(1,0), С(0,1)→С`(0,1). Это отображение является взаимно однозначным и значит, оно будет преобразованием плоскости γ на себя.

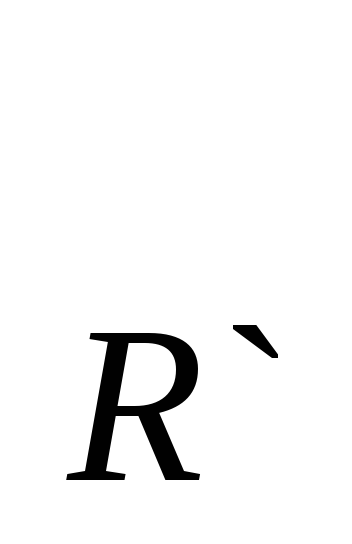
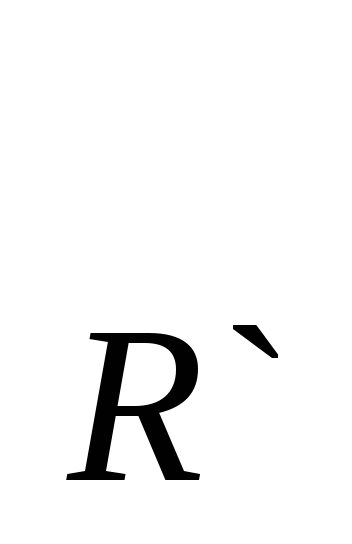
Докажем, что это преобразование сохраняет расстояние.

M₁M₂ =

M₁`M<sub>2</sub>`=

Значит, преобразование плоскости γ в себя является движением.

Докажем, что это движение единственное.

Предположим, что 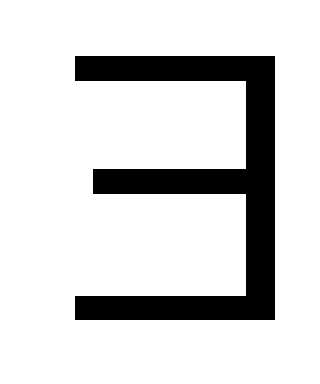движение g₁: γ→ γ.

При движении g₁ точка М(x,y)→М«(x,y).

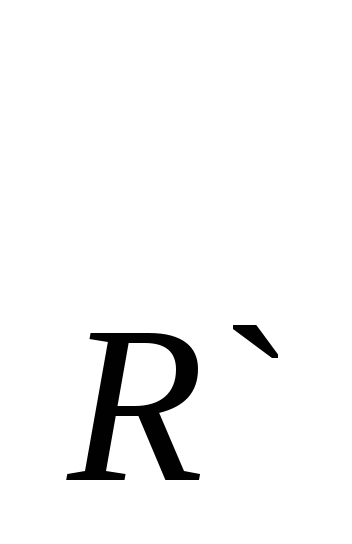
При движении g точка М(x,y)→М`(x,y).

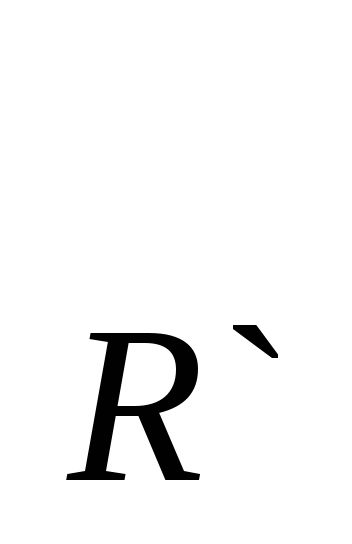
Точка А при движении g_1: AA` и АА` А`M`=A`M`. Значит, точка А` равноудалена от точек M` и M`.

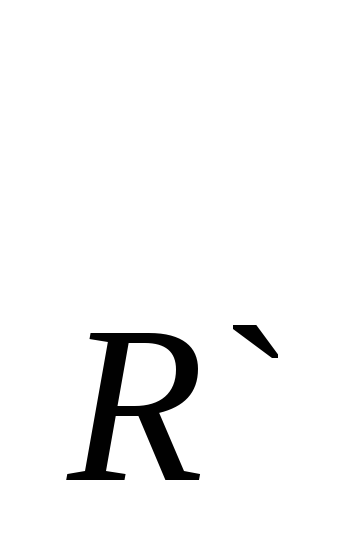
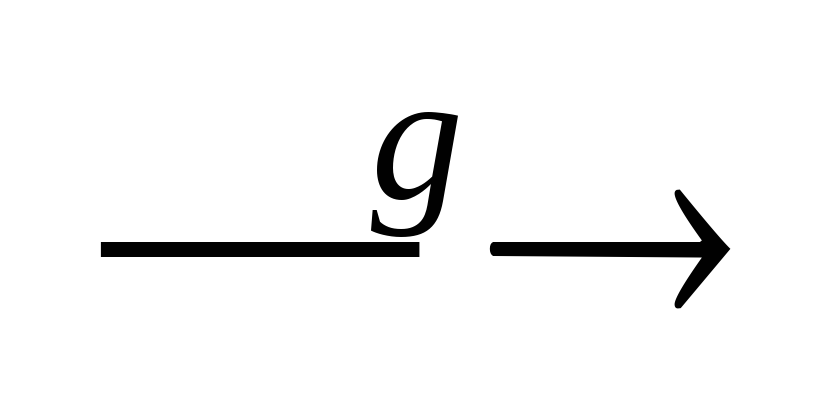
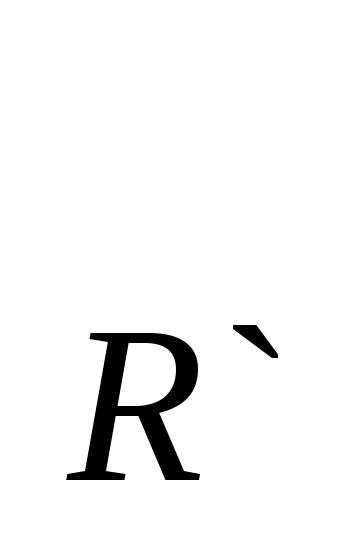
Аналогично показываем равноудаленность точек B` и C` от M` и M«.

Имеем, что точки A`, B`, C` располагаются на одной прямой (серединном перпендикуляре к отрезку M`M`), что противоречит условию теоремы или определению репера.

Следствие 15.4. В любом движении репер переходит в репер, в частности ортонормированный репер переходит в ортонормированный репер.

Движение переводит прямую в прямую, параллельную прямую в параллельную ей прямую.

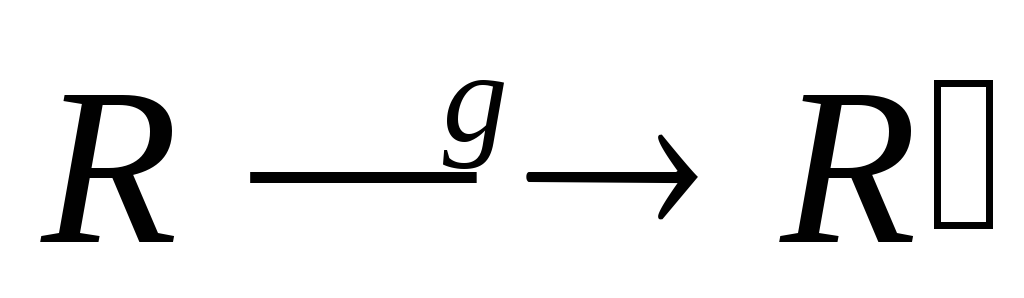
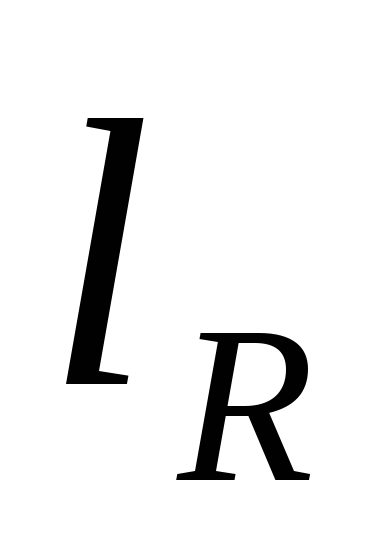
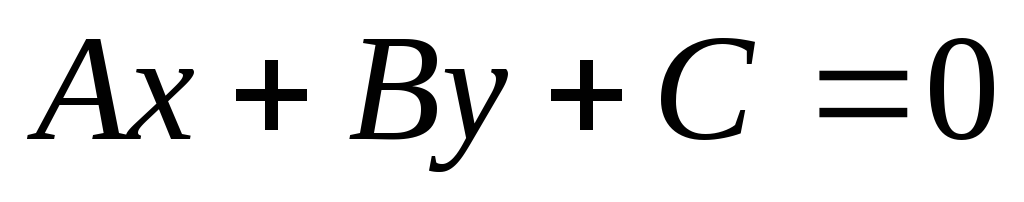
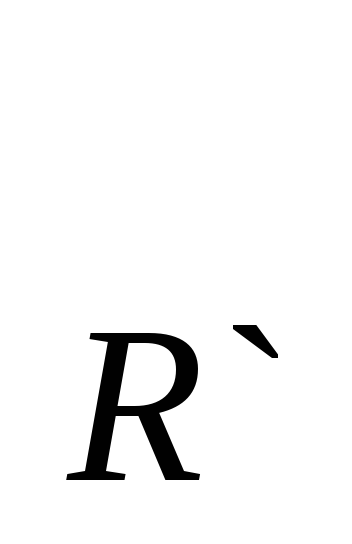
Дано , : . Каждая точка этой прямой при движении g будет переходить в точку репера R` с теми же координатами. Множество образов этих точек будет принадлежать прямой l`:

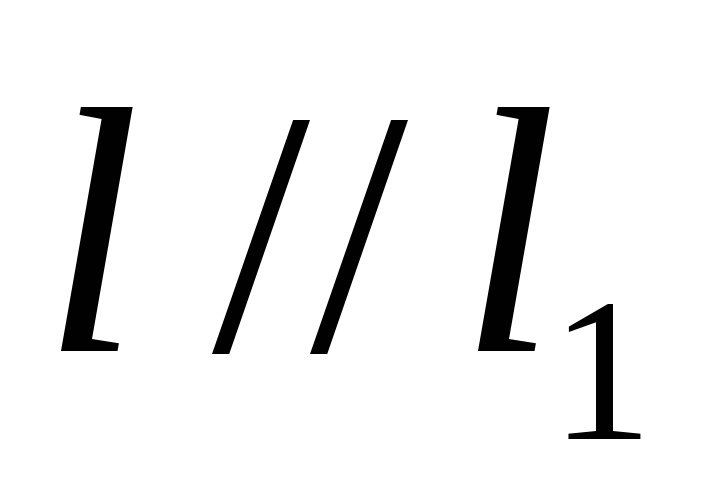
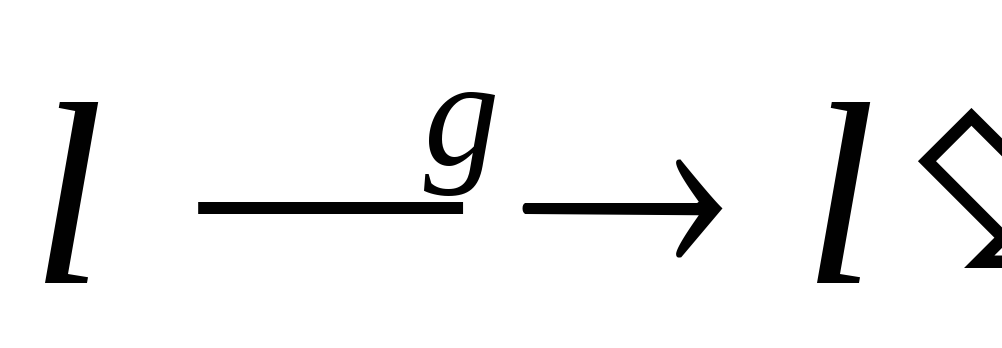
Пусть . При движении g: , .

Т.к. движение – это преобразование, а преобразование взаимно однозначно, то прообраз точки M` (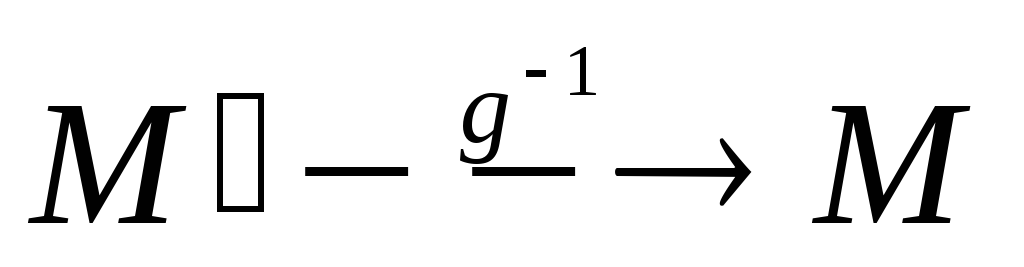) должен принадлежать как l так и l₁ (M l и M l₁) l l₁, что противоречит условию.

Движение переводит полуплоскость с границей A в полуплоскость с границей A`, где A`- образ прямой а;

Движение сохраняет простое отношение трех точек прямой;

Движение сохраняет отношение «лежать между»;

Движение переводит отрезок AB в отрезок A`B`. При этом середина отрезка AB переходит в середину отрезка A`B`;

Движение переводит угол в равный ему угол, луч в луч;

Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямые;

При движении флаг переводится во флаг (флагом называется тройка, состоящая из точки, луча и полуплоскости, где О – точка плоскости, h— луч, исходящий из этой точки, α – полуплоскость, граница которой содержит луч h)

Определение 15.5. Два репера, состоящие из R = (O, A, B) и R`= (O`, A`, B`), называются одинаково ориентированными (противоположно ориентированными), если базисы , и одинаково ориентированы (противоположно ориентированы).

Источник

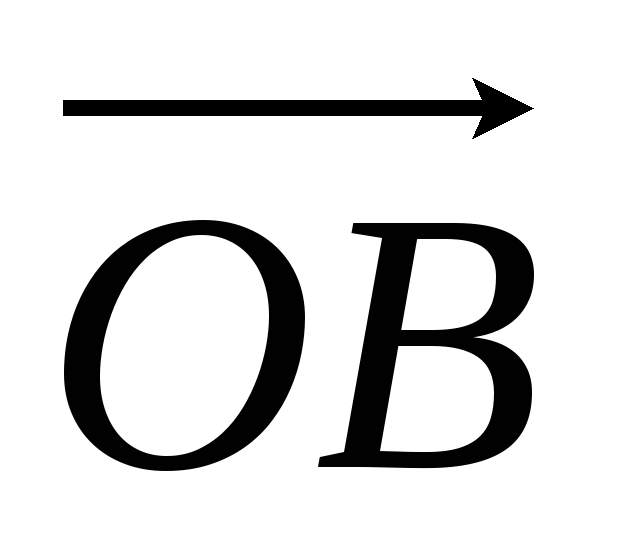
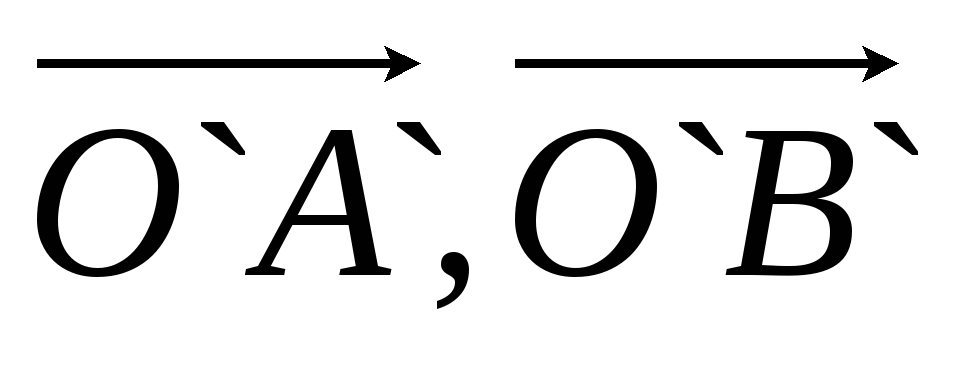
Что такое движение или перемещение плоскости

ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ
ТВЕРДОГО ТЕЛА

§ 15. Задание плоского движения твердого тела

Плоским или плоскопараллель­ным движением твердого тела называ­ется такое его движение, при котором ка­ждая точка тела движется в плоско­сти, параллельной некоторой неподвижной плоскости, например движение колеса ва­гона на прямолинейном участке пути, дви­жение шатуна кривошипно-шатунного ме­ханизма.

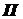
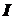
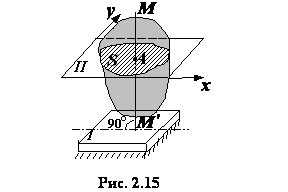
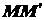
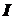
Рассмотрим движение плоской фи­гуры, представляющей собой сечение тела, находящегося в плоском движении, плоскость , параллельной неподвижной плоскости (рис. 2.15). При плоском движении все точки тела, лежащие на прямой , перпендику­лярной к сечению , т. е. к плоскости , движутся

тождественно. Поэтому вме­сто плоского движения тела достаточно изучить движение плоской фигуры в ее плоскости.

В кинематике твердого тела изучаются три основных вопроса: задание движе­ния тела, вычисление скорости ка­кой-либо его точки и вычисление ее уско­ре­ния. Кроме этих вопросов изучаются и другие вопросы, представляющие на­учный и технический интерес.

Положение движущейся плоской фигуры в ее плоскости относительно не­подвижной системы осей координат определя­ется положением какого-либо отрезка, жестко связанного с этой фигурой (рис. 2.16).

Положение отрезка можно определить, зная радиус-вектор точки и угол , который образует отрезок с осью . Точку называют полюсом. При движении тела величины и будут изменяться в зависимости от времени, т. е.

; (2.44)

. (2.45)

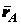
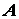
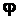
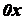
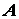
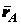
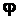
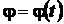
Уравнения (2.44) и (2.45) называются уравнениями плоского движения твердого тела.

Теорема. Всякое перемещение плоской фигуры в ее плоскости можно пред­ставить как совокупность двух перемещений: 1) поступательного переме­щения, зависящего от выбора полюса; 2) вращательного перемещения вокруг полюса; угол и направление поворота от выбора полюса не зависят.

фигуру посту­пательно в положение а затем по­вернем ее на угол вокруг точки . Заметим, что поступательное перемещение зависит от выбора полюса, а угол поворота не зависит от него. Действительно, тот же переход из положения в положе­ние можно осуществить, приняв за полюс точку и переместив сначала фигуру в положение (причем все точки фигуры получат перемещения, гео­метрически равные и отличные от , а затем повернув фигуру на во­круг точки .

, (2.46)

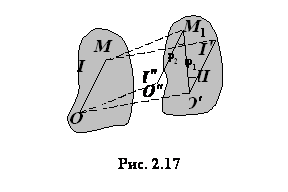
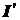
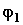
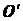
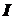
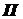
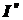
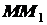
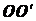
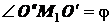
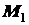
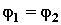
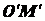
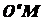
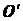
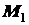
так как отрезки и параллельны и повороты вокруг точек и происходят в одну сторону.

Продифференцировав равенство (2.46), получим

; , (2.47)

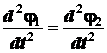
т. е. угловая скорость и угловое ускорение не зависят от выбора полюса пло­ской фигуры при плоском ее движении.

§ 16. Вычисление скорости точки тела при плоском

Положение любой точки плоской фигуры можно определить радиусом-вектором (рис. 2.18)

— вектор, определяющий положение точки относительно системы

, перемещающейся вместе с полюсом поступательно

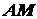
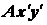
(движение тела по отно­шению к этой системе представляет собой

вращение вокруг полюса).

, (2.49)

получит при , т. е. относительно системы

, или, иначе, при вращении тела вокруг полюса .

Источник