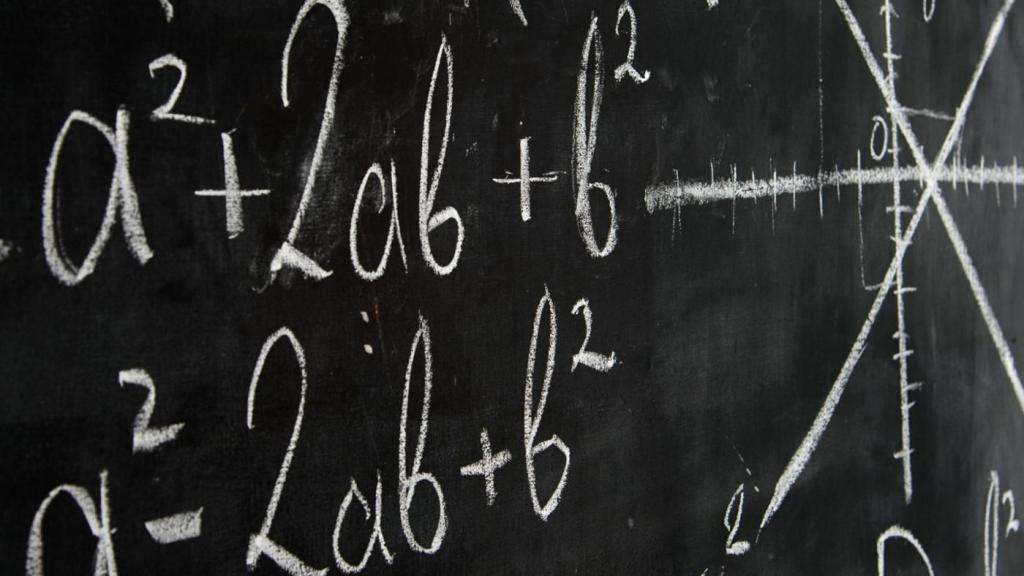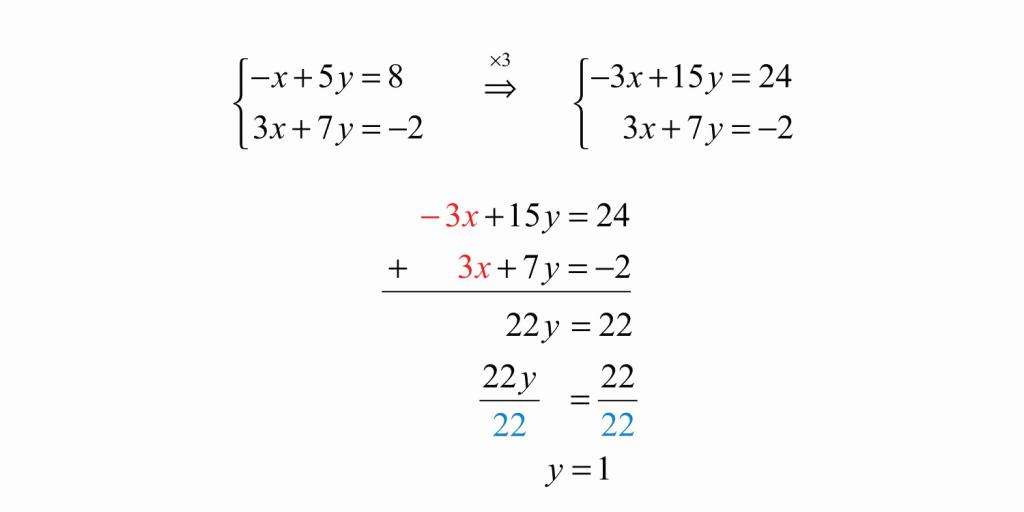что такое две переменные
Что такое две переменные
V . 1 . Дифференцируемость функции двух переменных
Функции двух переменных – частный случай функций нескольких (многих) переменных.
Пример 5.1. Найти область определения функции
Для функции двух (нескольких) переменных вводятся понятия предела функции, ее непрерывности и дифференцируемости в точке. Дадим понятие окрестности точки. δ-окрестностью точки M 0 ( x 0 ; y 0 ) называется совокупность всех внутренних точек круга радиуса δ с центром в точке M 0 или множество всех точек M ( x , y ) плоскости, координаты которых удовлетворяют неравенству 
Заметим, что для функции одной переменной стремление аргумента х к значению х0 возможно только по двум направлениям (справа и слева). Для функции двух переменных число таких направлений бесконечно, и если предел существует, то он не зависит от пути, по которому М стремится к М0.
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной.
Заметим, что полное приращение не равно сумме частных приращений.
– она определена в этой точке и некоторой ее окрестности,
Пример 5.2. Найти частные производные по переменным функции
Сумма первых двух слагаемых последнего равенства для ∆ z представляет собой главную часть приращения и называется полным дифференциалом dz функции двух переменных. Таким образом
Каждое слагаемое правой части равенства (5.6) называется частным дифференциалом функции двух переменных по переменной х и у соответственно.
Что такое переменные? Переменная величина в математике
Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.
Понятие переменной

Виды величин

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).
Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.
История
История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.
Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.
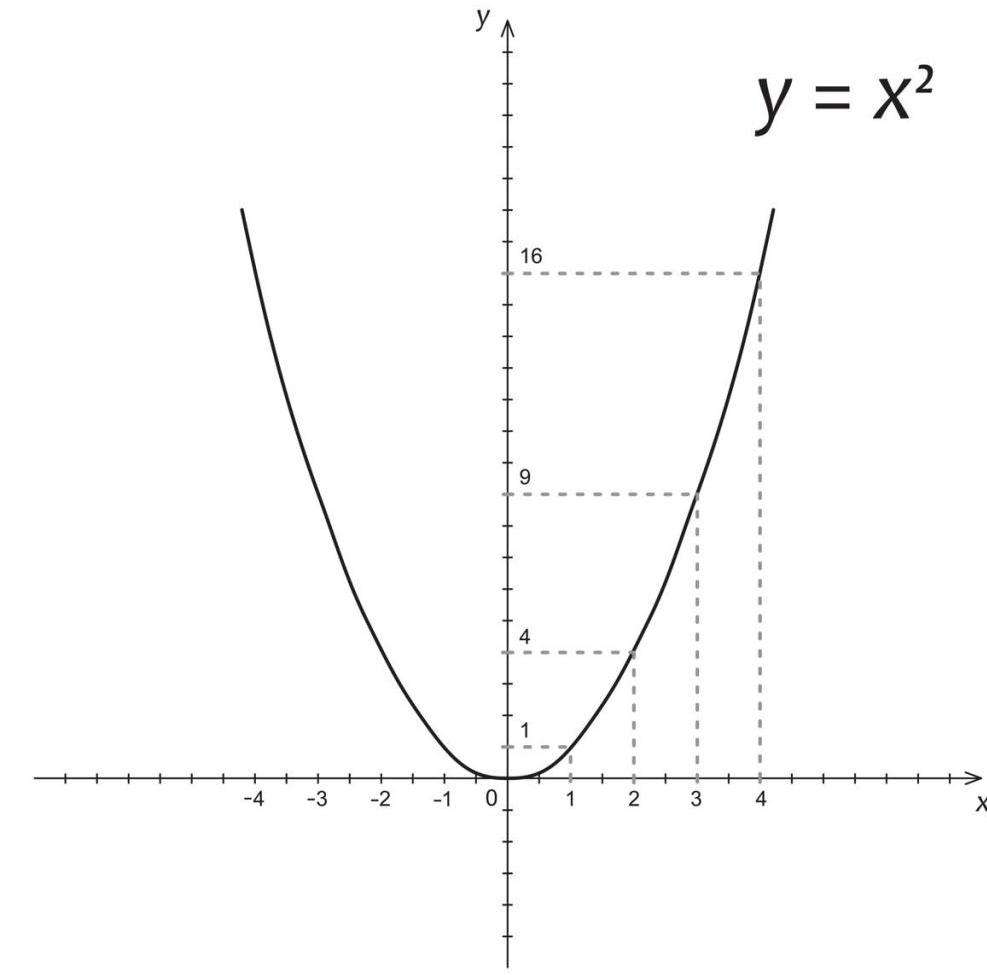
С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:
За x2 принимаем некое k, и уравнение приобретает понятный вид:
Вот какую пользу в математику несет введение переменных.
Неравенства, примеры решения
Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:
Пример с одной переменной:
Делим обе части неравенства на 10 и получаем:
Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.
Решением этого неравенства будет промежуток (20; +∞).
Решение нестрогого неравенства осуществляется так же, как и строгого:
Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.
Квадратные неравенства
Если взять квадратное уравнение вида ax2 + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.
Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.
По формуле корней квадратного уравнения получаем:
Или можно было решить это уравнение по теореме Виета:
Методом подбора получаем такие же корни уравнения.
Парабола
1. Определяем, куда направлены ветви параболы.
2. Приравниваем функцию к нулю и находим корни уравнения.
3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.
Выписываем в виде функции:
Приравниваем к нулю.
Дальше решаем как квадратное уравнение и находим нули функции:
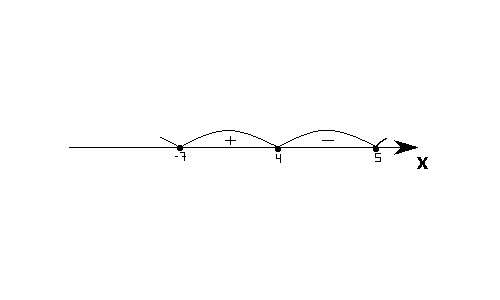
Метод интервалов
1. Находим корни уравнения, при которых неравенство равно нулю.
2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.
3. Определяем знак любого интервала.
4. Расставляем знаки у остальных интервалов, меняя их через один.
2) Изображаем их на числовой прямой.
3) Определяем знаки интервалов.
2. Отмечаем их на числовой прямой.
3. Определяем знаки интервалов.
Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.
Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.
Системы уравнений
Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.
Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.
Алгебраический метод
Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.
Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:
Решаем получившееся уравнение и находим икс.
Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:
Метод подстановки
Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.
В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:
Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:
Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:
Изучаем C++. Часть 2. Переменные, константы и операции с ними
Разбираемся, как работать с данными в программе на C++. Будет много теории и примеров, чтобы вы углубились в язык ещё больше.
Это вторая часть из серии «Глубокое погружение в C++». В прошлый раз мы разобрались, что такое программа и из чего она состоит, а сейчас узнаем азы работы с данными.
Что такое данные и как они хранятся в программах
Все программы работают с данными. Данные — это любые значения, которые используются в работе программы: строки, числа, ссылки и символы. Например: имя, возраст, количество денег на счету, здоровье персонажа в игре и так далее. Даже отсутствие данных — это данные.
Пишет о программировании, в свободное время создает игры. Мечтает открыть свою студию и выпускать ламповые RPG.
Все эти и другие значения хранятся в оперативной памяти. Для каждого значения выделяется отдельная ячейка, и одновременно в ней может находиться только что-то одно.
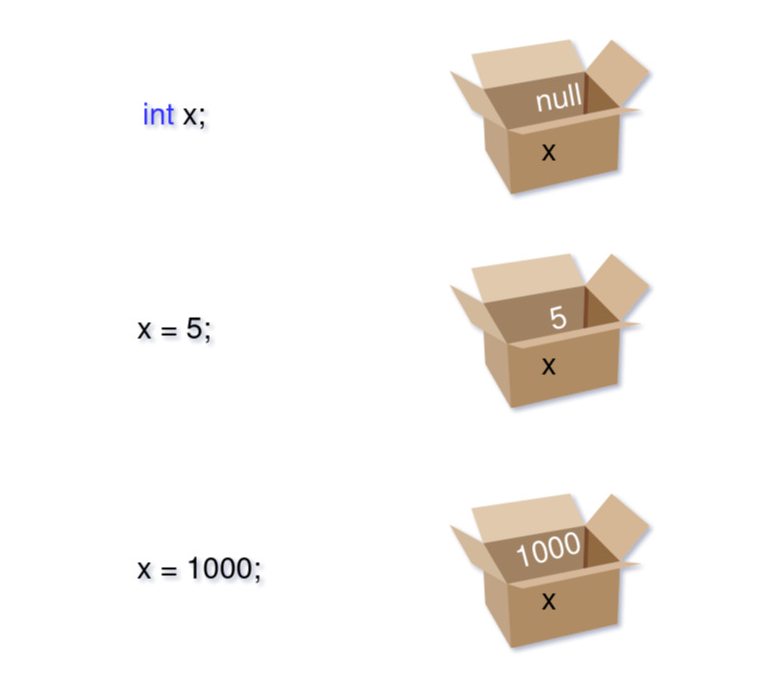
Давайте рассмотрим это на примере коробок:
Мы говорим компьютеру, что нам нужна коробка x, которая будет хранить целые числа, но пока не помещаем в неё никакого значения. Компьютер создаёт такую коробку, подписывает её и помещает в неё null.
Далее мы пишем команду x = 5;, и компьютер меняет значение внутри коробки. Размер коробки при этом не меняется. Так получается, потому что для хранения каждого примитивного типа данных выделяется определённое количество памяти. Например, для целых чисел это четыре байта, что позволяет хранить значения в диапазоне от −2 147 483 648 до 2 147 483 647.
Коробки, описанные выше, в программировании называются переменными (англ. variable). Их значение можно менять во время работы программы. Также существуют коробки, которые менять нельзя, — их называют константами.
То, какие данные сейчас хранятся в памяти, называется состоянием. Состояние может быть у программы, системы, компьютера и так далее. В C++ очень важно иметь доступ к состоянию, чтобы писать полезные программы.
Переменные в C++
Теперь попробуем создать свои переменные.
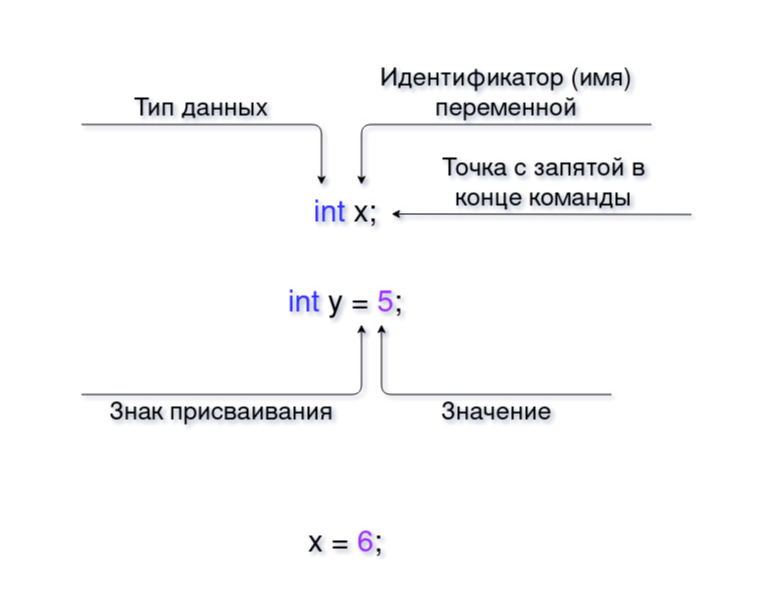
Для начала объявим переменную, то есть скажем компьютеру, что нам нужно занять место в памяти. Для этого укажем тип данных, а потом название переменной.
| Код | Как читается |
|---|---|
| int x; | Объявить целочисленную переменную x без значения. |
Так создаётся переменная без значения. Если вы хотите, чтобы в ней сразу было какое-то число, то нужно использовать знак присваивания (=):
| Код | Как читается |
|---|---|
| int y = 5; | Объявить целочисленную переменную y со значением 5. |
Теперь в любое время можно менять значения переменных:
| Код | Как читается |
|---|---|
| x = 6; | Присвоить переменной x значение 6. |
Математический знак равенства ( =) в программировании называется знаком присваивания.
Важно! Указывать тип данных нужно только при объявлении переменной.
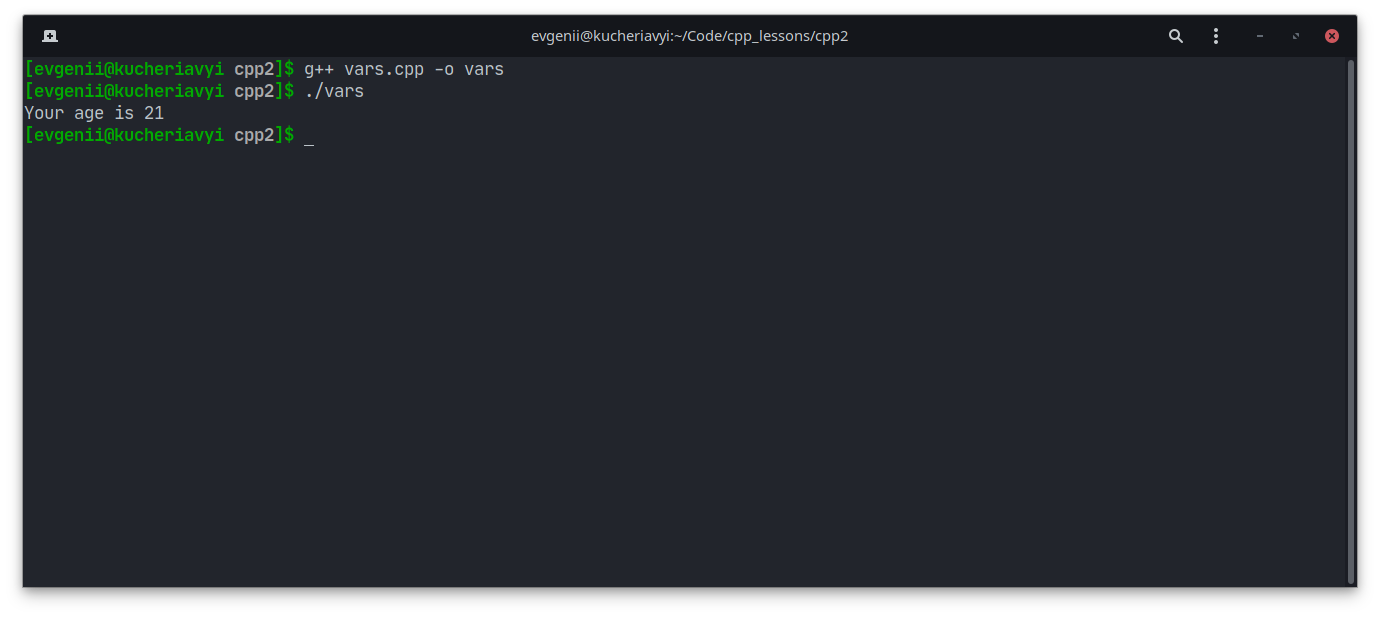
Давайте попробуем вывести значение какой-нибудь переменной на экран. Для этого напишем следующий код:
Внимательно прочтите этот код, а потом скомпилируйте и запустите программу:
Попробуйте изменить значение переменной age на любое другое число и посмотрите, как изменится вывод.
Допустимые имена для переменных
Идентификаторы переменных могут содержать в себе:
При этом название не может начинаться с цифр. Примеры названий:
Все идентификаторы регистрозависимы. Это значит, что name и Name — разные переменные.
Рекомендуется давать именам простые названия на английском языке, чтобы код был понятен и вам, и другим людям. Например:
Если название должно состоять из нескольких слов, то рекомендуется использовать camelCase (с англ. «верблюжий регистр»): первое слово пишется со строчной буквы, а каждое последующее — с заглавной.
Типы данных в программировании
Чаще всего используются следующие типы данных:
Также существуют ссылочные типы — такие переменные хранят в себе не само значение, а ссылку на него в оперативной памяти. К ссылочным типам относятся массивы, объекты, строки (так называют любой текст) и многое другое. Для строк используется тип std: string.
Вот несколько примеров переменных разных типов:
Комментарии в C++
В коде выше русский текст после двойных слэшей (//) — это комментарии. Они позволяют разработчикам делать заметки, объяснять код так, чтобы все могли в нём ориентироваться. Компилятор игнорирует комментарии, поэтому они никак не влияют на работу программы.
Есть два типа комментариев:
Попробуйте написать в коде и те, и другие комментарии, чтобы понять, как они работают.
Константы в C++
Чтобы создать константу, используйте ключевое слово const:
Константы обычно нужны, чтобы хранить какие-то постоянные величины из физики, математики или геометрии: число пи, ускорение свободного падения, скорость света и так далее. Однако вы можете хранить в них и другие значения, которые должны оставаться постоянными:
Математические операции в C++
В С++ есть пять базовых математических операций:
Используются они следующим образом:
Важно! Сначала выполняется правая часть выражения после знака =, а потом левая. То есть переменной не будет присвоено значения, пока не выполнены все вычисления. Поэтому можно записать в переменную результат вычислений, в которых использовалась эта же переменная:
Если вам нужно провести какую-то операцию с переменной, а потом записать значение в неё же, используйте следующие операторы:
Во время работы с С++ вы будете часто прибавлять или отнимать единицу от какой-нибудь переменной. Для этого тоже есть сокращённая запись:
Инкремент и декремент могут быть префиксными (++x) и постфиксными (x++). Префиксный инкремент сначала прибавляет к переменной единицу, а потом использует эту переменную, а постфиксный — наоборот.
Функции нескольких переменных
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Любое отображение D->R называют функцией двух переменных с областью определения D и пишут z = f(x;y).
Если каждой паре (х; у) двух независимых переменных из области D по некоторому правилу ставится в соответствие одно определенное значение z из R, то переменную величину z называют функцией двух независимых переменных х и у с областью определения D и пишут
Аналогичным образом определяются функции многих переменных
П р и м е р 1. Найти и изобразить область определения функции
Область определения – есть плоскость хОу за исключением точек, лежащих на параболе у = х2, см. рисунок.
П р и м е р 2. Найти и изобразить область определения функции
П р и м е р 3. Найти и изобразить область определения функции

К числу функций нескольких переменных относятся производственные функции.
Производственными функциями называют функции, представляющие зависимости величин объемов выпускаемой продукции от переменных величин затрат ресурсов.
Производственные функции применяются не только в микроэкономических, но и в макроэкономических расчетах.
2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФУНКЦИИ ДВУХ
2.1.График функции двух переменных
Рассмотрим в пространстве прямоугольную систему координат и область D на плоскости хОу. В каждой точке М(х;у) из этой области восстановим перпендикуляр к плоскости хОу и отложим на нем значение z = f(x; у). Геометрическое место полученных точек
является пространственным графиком, функции двух переменных.
Это некоторая поверхность.
Равенство z = f(x; у) называется уравнением этой поверхности.
Линией уровня функции двух переменных z = f(x; у) называется линия f(x; у) = С (С = const) на плоскости хОу, в каждой точке которой функция сохраняет постоянное значение С.
Линия уровня представляет собой сечение поверхности графика функции двух переменных z = f(x; у) плоскостью z = С.
Поверхностью уровня функции трех переменных
u = f(x; у; z) называется поверхность в R3 (трехмерном пространстве), в каждой точке которой функция сохраняет постоянное значение f(x;y;z) = C (С = const).
П р и м е р. Найти и построить линии уровня функции

Линии уровня z = С данной функции имеют уравнения
Это окружности с центром в начале координат, радиусом R = C1/2 и уравнением
x2 + y2 = R2, см. рисунок.
Линии уровня позволяют представить рассматриваемую поверхность, дающую в сечении плоскостями z = C концентрические окружности.
При построении графика функции часто пользуются методом сечений.
П р и м е р. Построить график функции 

Решение. Воспользуемся методом сечений.






Искомая поверхность – параболоид вращения.
Расстоянием между двумя произвольными точками 


Множество точек 
Открытый круг радиуса ε с центром в точке A называется — ε — окрестностью точки А.
Найти и изобразить графически область определения функции:
Построить линии уровня функций:
3. ПРЕДЕЛ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
Основные понятия математического анализа, введенные для функции одной переменной, распространяются и на функции нескольких переменных.
О п р е д е л е н и е:
Постоянное число А называется пределом функции двух переменных z = f(x;у) при х —> х0, у —> у0, если для любого
Постоянное число А называется пределом функции двух переменных f(x;y) = f(M) при стремлении точки М к точке М0, если для любого ε >0 можно найти такое число г >0, что как только расстояние |М0М| 0.
Предел отношения 
водной функции z = f(х; у) в точке (х; у) по направлению вектора 
Переходя к этому пределу, получим

Таким образом, зная частные производные функции
z = f(x; у) можно найти производную этой функции по любому направлению, а каждая частная производная является частным случаем производной по направлению.
П р и м е р. Найти производную функции
в точке М(1;0) в направлении, составляющем с Ох угол в 30°.
Следовательно, функция z = f(x;y) в данном направлении возрастает.
Градиентом функции z = f(x; у) называется вектор 
Связь между производной функции по направлению и градиентом этой функции осуществляется соотношением
т. е. производная функции z = f(x;y) в данном направлении 
Градиент функции в каждой точке направлен по нормали к соответствующей линии уровня данной функции.
Направление градиента функции в данной точке есть направление наибольшей скорости возрастания функции в этой точке.