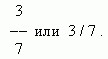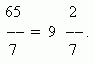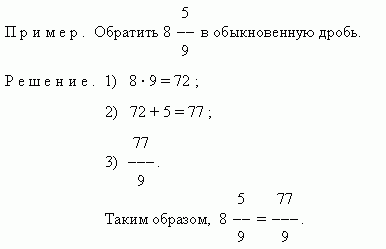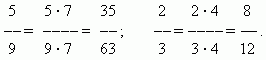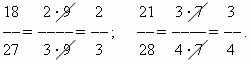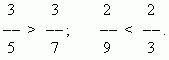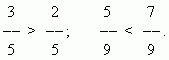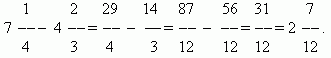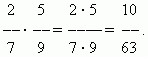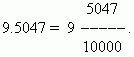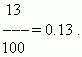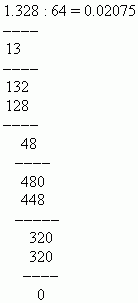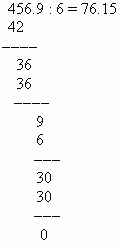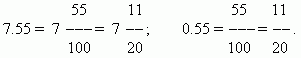что такое дробное выражение в алгебре

Алгебра. 8 класс

Целые выражения – это такие выражения, которые состоят из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число, отличное от нуля.

Дробные выражения – это выражения, которые помимо действий сложения, вычитания, умножения и деления на число, отличное от нуля, содержат деление на выражение с переменными.

Целые и дробные выражения вместе называют рациональными выражениями.

Дробь – это выражение вида .

Целое выражение имеет смысл при любых значениях входящих в него переменных, потому что действия для нахождения значения целого выражения, всегда возможны.

Дробное выражение при некоторых значениях переменной может не иметь смысла.

• не имеет смысла при x = 0.
• не имеет смысла при x = y.

Дробные выражения имеют смысл при любых значениях входящих в них переменных, кроме тех, что обращают знаменатель в нуль.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями.

Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.

Примеры

В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.

Чтобы найти допустимые значения переменных в дроби, необходимо:

• Приравнять знаменатель, содержащий переменные, к нулю.
• Решить полученное уравнение. Корни этого уравнения будут являться теми значениями переменных, которые обращают знаменатель в нуль.
• Исключить эти значения из всех действительных чисел.

Пример 1.
Найти допустимые значения переменной в дроби .

1) x(x + 1) = 0
2) x = 0 или x + 1 = 0
x = 0 или x = –1.
Корни уравнения 0 и – 1.
3) Допустимыми значениями x являются все числа, кроме 0 и –1.

Пример 2.
Найти значения x, при которых дробь равна нулю.

, когда x 2 – 1 = 0 и x + 1 ≠ 0.
1) x 2 – 1 = 0
2) (x – 1)(x + 1) = 0
x = ±1
3) x + 1 ≠ 0
x ≠ –1.
при x = 1.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.

Источник

Обыкновенные (простые) дроби

Обыкновенная (простая) дробь. Числитель и знаменатель дроби.

Правильная и неправильная дробь. Смешанное число.

Неполное частное. Целая и дробная часть. Обратные дроби.

Часть единицы или несколько её частей называютсяобыкновенной или простой дробью. Количество равных частей, на которые делится единица, называется знаменателем, а количество взятых частей – числителем. Дробь записывается в виде:

Здесь 3 – числитель, 7 – знаменатель.

Если числитель меньше знаменателя, то дробь меньше 1 и называется правильной дробью. Если числитель равен знаменателю, то дробь равна 1. Если числитель больше знаменателя, то дробь больше 1. В обоих последних случаях дробь называется неправильной. Если числитель делится на знаменатель, то эта дробь равна частному от деления: 63 / 7 = 9. Если деление выполняется с остатком, то эта неправильная дробь может быть представлена смешанным числом:

Здесь 9 – неполное частное (целая часть смешанного числа), 2 – остаток (числитель дробной части), 7 – знаменатель.

Обратные дроби – это две дроби, произведение которых равно 1. Например, 3 / 7 и 7 / 3 ; 15 / 1 и 1 / 15 и т.д.

Действия с обыкновенными дробями

Расширение дроби. Сокращение дроби. Сравнение дробей.

Приведение к общему знаменателю. Сложение и вычитание дробей.

Умножение дробей. Деление дробей.

Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.

Использованное здесь преобразование называется приведением дробей к общему знаменателю.

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.

Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.

Десятичные дроби

Десятичные дроби

Десятичная дробь. Целая часть. Десятичная точка.

Десятичные знаки. Свойства десятичных дробей.

Периодическая десятичная дробь. Период.

Десятичная дробь есть результат деления единицы на десять, сто, тысячу и т.д. частей. Эти дроби очень удобны для вычислений, так как они основаны на той же позиционной системе, на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями фактически те же, что и для целых чисел. При записи десятичных дробей нет необходимости отмечать знаменатель, это определяется местом, которое занимает соответствующая цифра. Сначала пишется целая часть числа, затем справа ставитсядесятичная точка. Первая цифра после десятичной точки означает число десятых, вторая – число сотых, третья – число тысячных и т.д. Цифры, расположенные после десятичной точки, называются десятичными знаками.

Если десятичная дробь не содержит целой части, то перед десятичной точкой ставится ноль:

Свойства десятичных дробей.

1. Десятичная дробь не меняется, если справа добавить нули:

2. Десятичная дробь не меняется, если удалить нули, расположенные

в конце десятичной дроби:

Внимание! Нельзя удалять нули, расположенные не в конце десятичной дроби!

Десятичная дробь возрастает в 10, 100, 1000 и т.д. раз, если перенести

десятичную точку на одну, две, три и т.д. позиций вправо :

Десятичная дробь уменьшается в 10, 100, 1000 и т.д. раз, если перенести

десятичную точку на одну, две, три и т.д. позиций влево:

Эти свойства позволяют быстро умножать и делить десятичные дроби на 10, 100, 1000 и т.д.

Периодическая десятичная дробь содержит бесконечно повторяющуюся группу цифр, называемую периодом. Период записывается в скобках. Например, 0.12345123451234512345… = 0.(12345).

Действия с десятичными дробями

Сложение и вычитание десятичных дробей.

Умножение десятичных дробей.

Деление десятичных дробей.

Сложение и вычитание десятичных дробей. Эти операции выполняются так же, как и сложение и вычитание целых чисел. Необходимо только записать соответствующие десятичные знаки один под другим.

Умножение десятичных дробей. На первом этапе перемножаем десятичные дроби как целые числа, не принимая во внимание десятичную точку. Затем применяется следующее правило:количество десятичных знаков в произведении равно сумме десятичных знаков во всех сомножителях.

Сумма чисел десятичных знаков в сомножителях равна: 3 + 4 = 7. Сумма цифр в произведении равна 6. Поэтому необходимо добавить один ноль слева: 0197056 и проставить перед ним десятичную точку: 0.0197056.

Деление десятичных дробей

Деление десятичной дроби на целое число

Если делимое меньше делителя, записываем ноль в целой части частного и ставим после него десятичную точку. Затем, не принимая во внимание десятичную точку делимого, присоединяем к его целой части следующую цифру дробной части и опять сравниваем полученную целую часть делимого с делителем. Если новое число опять меньше делителя, ставим ещё один ноль после десятичной точки в частном и присоединяем к целой части делимого следующую цифру его дробной части. Этот процесс повторяем до тех пор, пока полученное делимое не станет больше делителя. После этого деление выполняется, как для целых чисел. Если делимое больше делителя или равно ему, сначала делим его целую часть, записываем результат деления в частном и ставим десятичную точку. После этого деление продолжается, как в случае целых чисел.

Р е ш е н и е :

Деление одной десятичной дроби на другую.

Сначала переносим десятичные точки в делимом и делителе на число десятичных знаков в делителе, то есть делаем делитель целым числом. Теперь выполняем деление, как в предыдущем случае.

Р е ш е н и е. Переносим десятичные точки на 4 позиции вправо и делим 456.9 на 6:

Арифметические действия со смешанными дробями

Обращение десятичной дроби в обыкновенную и обратно

В большинстве случаев этот процесс может продолжаться бесконечно. Тогда невозможно точно обратить обыкновенную дробь в десятичную. Но на практике это никогда и не требуется. Деление прерывается, если представляющие интерес десятичные знаки уже получены.

Источник

Урок 20 Бесплатно Дробные выражения

В этом уроке мы познакомимся с понятием дробных выражений и с тем, как их считать. Узнаем интересные способы работы с дробями, в числителе или знаменателе которых стоят дроби.

Дробные выражения

Для начала определимся с определением дробного выражения.

Дробным выражением называется частное двух выражений или чисел, знак деления в котором обозначается чертой.

Пример:

Мы привыкли называть такое выражение обыкновенной дробью. Она ничем не противоречит определению дробного выражения. Поэтому если вас спросят: «Является ли обыкновенная дробь дробным выражением?», то можно смело ответить: «Да, является!»

Мы не накладываем никаких ограничений на то, что из себя представляют выражения; нужно только то, чтобы это было деление, записанное как дробь.

Также никто не запрещает записать в одну или даже в обе части выражения, содержащие дроби.

Примеры:

Можем пойти дальше и записать так называемую многоэтажную дробь. Это дробь, в числителе или в знаменателе (а иногда и в числителе и в знаменателе) которой стоят дробные выражения.

Примеры:

Помимо определения дробного выражения необходимо знать определения числителя и знаменателя дробного выражения.

Если мы считаем дробное выражение делением, то числителем будет являться делимое, а знаменателем делитель.

Например, существует следующее дробное выражение:

В данном случае \(\mathbf<3+10\cdot2>\) будет являться числителем, а \(\mathbf<2+\frac<1><2>>\)- знаменателем.

Также можно преобразовывать обычные выражения в дробные.

Это можно делать при условии, что выражение представляет из себя частное двух выражений или чисел, но пока что записанное через обычный знак деления.

Примеры преобразования обычного выражения в дробное:

Сформулируем правило: для того, чтобы преобразовать выражение, представляющее из себя частное двух выражений или чисел, необходимо делимое поместить в числитель дробного выражения, а делитель- в знаменатель.

Теперь вы видите, насколько большой класс формул покрывается понятием дробного выражения.

Давайте пройдем небольшой тест и перейдем к изучению того, как вычислять значения дробных выражений.

Пройти тест и получить оценку можно после входа или регистрации

Вычисление дробных выражений

Начнем с самого простого способа вычисления значений дробных выражений.

Он заключается в том, чтобы отдельно посчитать значения числителя и знаменателя и получить дробное выражение, в знаменателе и числителе которого стоят числа.

Далее надо смотреть, что получилось:

Пример 1

Вычислим значение выражения \(\mathbf<\frac<1+2\cdot4><5-2>>\)

Решение:

Для начала вычислим значения числителя и знаменателя:

В данном примере числитель делится на знаменатель, поэтому из дроби получится натуральное число.

Пример 2

Решение:

Сначала вычислим числитель и знаменатель:

В данном случае получилась неправильная дробь, выделим целую ее часть, чтобы получить в ответе смешанное число:

Пока что были рассмотрены случаи, в которых выражения в числителе и знаменателе представляли из себя арифметические действия над натуральными числами. Но вас нисколько не должны смущать случаи, в которых выражения содержат в себе дроби как обыкновенные, так и десятичные.

Пример:

Решение:

Наверное, вы уже догадываетесь, что мы сделаем дальше. Правильно! Вычислим числитель и знаменатель:

В данном случае мы получили неправильную дробь в числителе и десятичную дробь в знаменателе.

Чтобы получить окончательный результат разделим одно на другое:

Прежде чем перейти к дополнительным приемам работы с дробными выражениями, решим небольшой тест для закрепления навыка вычисления дробных выражений.

Пройти тест и получить оценку можно после входа или регистрации

Приемы для работы с дробными выражениями

Пока что во всех предыдущих случаях мы находили значения дробных выражений «в лоб», по достаточно простому алгоритму.

Но, как это часто бывает в математике, в некоторых случаях можно упростить себе подсчеты, вовремя заметив определенные вещи.

Вы уже наверняка хорошо освоили сокращение дробей.

Напомним, в чем его суть: если числитель представляет из себя произведение, и знаменатель также является произведением, и в этих произведениях есть одинаковый множитель, то мы можем сократить дробь на этот множитель.

Как же это относится к дробным выражениям?

Дело в том, что в некоторых случаях числитель и знаменатель могут быть произведениями или же могут стать произведениями в процессе подсчетов.

Тогда почему бы не сокращать их по возможности?!

Пример:

Начнем считать выражение и посмотрим, что получается.

Числитель и знаменатель дробного выражения после первых преобразований превратились в произведения.

Также можно заметить, что в этих произведениях есть общий множитель: 127

Тогда мы можем поделить числитель и знаменатель дробного выражения на это число, тем самым значительно упростив выражение.

Это и будет значением этого выражения.

Также мы можем быть еще более хитрыми и внимательными.

Конечно же, можно начать вычислять сначала числитель, потом знаменатель. Для этого мы будем вычислять разность шестизначных чисел.

Но можно сделать проще: заметим, что числитель и знаменатель являются произведениями.

Числитель является произведением 2-х и выражения (478569-145236)

Знаменатель же является произведением выражения (478569-145236) и 3-х.

Выражение (478569-145236) является множителем и можно утверждать, что это один и тот же множитель в числителе и в знаменателе.

Значит, мы можем уверенно сокращать дробное выражение на это выражение.

В данном случае мы сразу получили правильную дробь, это и будет являться значением выражения.

Отдельно стоит упомянуть работу с многоэтажными дробями.

Но также можно запомнить два правила, которые существенно экономят время.

Первое правило говорит о том, что, если в числителе дробного выражения находится дробь (или же дробное выражение), мы можем домножить дробное выражение на знаменатель дроби (или дробного выражения), стоящей в числителе, тем самым уменьшив «этажность» дробного выражения.

Второе правило рассматривает случай, когда дробь (или дробное выражение) находится в знаменателе дробного выражения.

В таком случае уменьшить «этажность» дробного выражения поможет домножение всего дробного выражения на знаменатель дроби (или дробного выражения), стоящей в знаменателе.

И парочка примеров на этот случай:

И в завершение еще дам такой пример:

Пройти тест и получить оценку можно после входа или регистрации

Интересная информация

Десять интересных математических фактов:

1. Известные всем знаки сложения и вычитания впервые были использованы только около 500 лет назад

2. 2 и 5— единственные простые числа, которые оканчиваются на 2 или 5

3. Несмотря на то, что сохранилось много трудов древнегреческого ученого Евклида, о его биографии почти ничего не известно

4. В римской системе счисления не существует нуля

5. Знак равенства «=» появился только в XVI веке

6. Слово «миг» обозначает не только короткое мгновение, но и вполне конкретный временной промежуток: 0,01 секунды

7. У древних египтян отсутствовала таблицы умножения и прочие математические правила

8. В свое время заниматься математикой в высоких кругах было настолько популярно, что даже Наполеон Бонапарт оставил после себя научные труды

9. Самые древние математические записи были найдены написанными на костях

10. Ученый Муавр с помощью математики смог рассчитать дату своей смерти

Заключительный тест

Пройти тест и получить оценку можно после входа или регистрации

Источник

Обыкновенные дроби

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

Виды дробей:

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Полученные числа запишем справа сверху над числителем.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

Источник