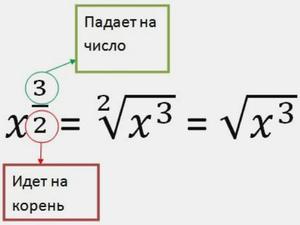
что такое дробная отрицательная степень числа
Отрицательная дробная степень числа
Как посчитать отрицательную дробную степень числа на калькуляторе разберем пример!? + Разберем формулу «число в отрицательной дробной степени«
Сегодня этим и займемся!
Как возвести число в отрицательную дробную степень
Считаем отрицательную дробную степень числа формула
Чем отличается положительная дробная степень числа от отрицательной дробной степени числа!?
Тем, что после того, как вы посчитаете дробную степень числа, нужно единицу разделить на получившийся результат! Элементарно!
Разберем формулу число в отрицательной дробной степени
Возьмем ранее разобранный вариант на странице
И добавим минус, что и будет отрицательной дробной степенью числа
Пример подсчета : «число в отрицательной дробной степени на калькуляторе»
В этом пункте разберем, как можно посчитать отрицательную дробную степень числа на калькуляторе, но вначале напишем тот алгоритм, который рассматривали выше, и унас получится:
Набираем число 125 и нажимаем число степени
Теперь нам нужно набрать отрицательную степень. Набираем одну третью и ставим знак минус – нажимаем равно!
Результат возведения числа в отрицательную степень.
Отрицательная степень числа: правила возведения и примеры
В одной из предыдущих статей мы уже упоминали о степени числа. Сегодня мы постараемся сориентироваться в процессе нахождения ее значения. Научно говоря, мы будем выяснять, как правильно возводить в степень. Мы разберемся, как производится этот процесс, одновременно затронем все вероятные показатели степени: натуральный, иррациональный, рациональный, целый.
Итак, давайте подробно рассмотрим решения примеров и выясним, что значит:
Определение понятия
Вот точно отражающее смысл определение: «Возведением в степень называют определение значения степени числа».
Соответственно, возведение числа a в ст. r и процесс нахождения значения степени a с показателем r — это идентичные понятия. К примеру, если стоит задача вычислить значение степени (0,6)6″, то ее можно упростить до выражения «Возвести число 0,6 в степень 6».
После этого можно приступать напрямую к правилам возведения.
Возведение в отрицательную степень
Минусовая степень обозначает, что число множат на него самого такое количество раз, какое значится в ст., а после этого единицу делят на вычисленный результат.
Для наглядности следует обратить внимание на такую цепочку выражений:
110=0,1=1* 10 в минус 1 ст.,
1100=0,01=1*10 в минус 2 степ.,
11000=0,0001=1*10 в минус 3 ст.,
110000=0,00001=1*10 в минус 4 степeни.
Благодаря данным примерам можно четко просмотреть возможность моментально вычислить 10 в любой минусовой степени. Для этой цели достаточно банально сдвигать десятичную составляющую:
Так же легко понять по данной схеме, сколько будет составлять 10 в минус 5 ст. —
Как возвести число в натуральную степeнь
Вспоминая определение, учитываем, что натуральное число a в ст. n равняется произведению из n множителей, при этом каждый из них равняется a. Проиллюстрируем: (а*а*…а)n, где n — это количество чисел, которые умножаются. Соответственно, чтобы a возвести в n, необходимо рассчитать произведение следующего вида: а*а*…а разделить на n раз.
Отсюда становится очевидно, что возведение в натуральную ст. опирается на умение осуществлять умножение (этот материал освещен в разделе про умножение действительных чисел). Давайте рассмотрим задачу:
Мы имеем дело с натуральным показателем. Соответственно, ход решения будет следующим: (-2) в cт. 4 = (-2)*(-2)*(-2)*(-2). Теперь осталось только осуществить умножение целых численностей:(-2)*(-2)*(-2)*(-2). Получаем 16.
Пример:
Вычислите значение: три целых две седьмых в квадрате.
Данный пример равняется следующему произведению: три целых две седьмых умножить на три целых две седьмых. Припомнив, как осуществляется умножение смешанных чисел, завершаем возведение:
Возведение в иррациональную стeпeнь
Касаемо вопроса возведения в иррациональный показатель, следует отметить что расчеты начинают проводить после завершения предварительного округления основы степени до какого-либо разряда, который позволил бы получить величину с заданной точностью. К примеру, нам необходимо возвести число П (пи) в квадрат.
Начинаем с того, что округляем П до сотых и получаем:
П в квадрате = (3,14)2=9,8596. Однако если сократить П до десятитысячных, получим П=3,14159. Тогда возведение в квадрат получает совсем другое чиcло: 9,8695877281.
Здесь следует отметить, что во многих задачах нет надобности возводить иррациональные числа в cтeпeнь. Как правило, ответ вписывается или в виде, собственно, степени, к примеру, корень из 6 в степени 3, либо, если позволит выражение, проводится его преобразование: корень из 5 в 7 cтепeни = 125 корень из 5.
Как возвести чиcло в целую степень
Эту алгебраическую манипуляцию уместно принимать во внимание для следующих случаев:
Поскольку практически все целые положительные числа совпадают с массой чисел натуральных, то постановка в положительную целую степень — это тот же процесс, что и постановка в ст. натуральную. Данный процесс мы описали в предшествующем пункте.
Теперь поговорим о вычислении ст. нулевой. Мы уже выяснили выше, что нулевую степень числа a можно определить для любого отличного от нуля a (действительного), при этом a в ст. 0 будет равно 1.
Соответственно, возведение какого угодно действительного числа в нулевую ст. будет давать единицу.
К примеру, 10 в ст.0=1, (-3,65)0=1, а 0 в ст. 0 нельзя определить.
Пример:
Вычислить значение числа 2 в кубе с целым отрицательным показателем.
Согласно определению стeпeни с отрицательным показателем обозначаем: два в минус 3 ст. равняется один к двум в третьей cтепeни.
Знаменатель рассчитывается просто: два в кубе;
Ответ: два в минус 3-й ст. = одна восьмая.
Видео
Из этого видео вы узнаете, что делать, если степень с отрицательным показателем.
Отрицательная степень числа
Степень с отрицательным показателем
Число с отрицательным показателем степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем.
Чтобы разобраться, почему число в отрицательной степени равно дроби, надо вспомнить правило деления степеней с одинаковыми основаниями:
При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя.
Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Пример 1. Замените дробь степенью с отрицательным показателем:
Пример 2. Представьте в виде степени с отрицательным показателем:
Действия над степенями с отрицательными показателями
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:
Чтобы возвести произведение в отрицательную степень, надо возвести в эту степень каждый сомножитель отдельно:
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются:
Отрицательная степень
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.
Как возвести число в отрицательную степень
Чтобы возвести число в отрицательную степень нужно:
Общая формула возведения в отрицательную степень выглядит следующим образом.
Примеры возведения в отрицательную степень.
Любое число в нулевой степени — единица.
Примеры возведения в нулевую степень.
Как найти 10 в минус 1 степени
В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».
Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «
| 1 |
| 10 |
» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».
Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
По такому же принципу можно найти « 10 » в минус второй, третьей и т.д.
Для упрощения перевода « 10 » в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один ».
Проверим правило выше для « 10 −2 ».
Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».
Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».
То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.
Как возвести в отрицательную степень дробь
Чтобы возвести дробь в отрицательную степень нужно:
Пример. Требуется возвести в отрицательную степень дробь.
Перевернем дробь «
| 10 |
| 3 |
» и заменим отрицательную степень « −3 » на положительную « 3 ».
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.
(
| 10 |
| 3 |
) −3 = (
| 3 |
| 10 |
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
(
| 10 |
| 3 |
) −3 = (
| 3 |
| 10 |
) 3 =
| 3 3 |
| 10 3 |
=
| 27 |
| 1000 |
= 0,027
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.
Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».
Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Разберемся на примере. Задание: возвести отрицательную дробь « (−
| 2 |
| 3 |
) » в « −3 » степень.
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».
Теперь определим конечный знак результата возведения в « 3 » степень.
Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.
Для окончательного ответа выделим целую часть из дроби.
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
(−
| 9 |
| 11 |
) −2 = (−
| 11 |
| 9 |
) 2 =
| 11 2 |
| 9 2 |
=
| 121 |
| 81 |
= 1
| 40 |
| 81 |
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.
Примеры решений заданий с отрицательной
степенью
Колягин 9 класс. Задание № 1
Представить в виде степени.
Колягин 9 класс. Задание № 5
Записать в виде степени с отрицательным числом.
Возведение в степень: правила, примеры
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Решение
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Решение
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Решение
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи 
От основания степени это не зависит.
Как возвести число в целую степень
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Решение
Решение
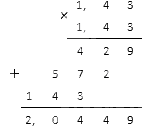
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
Как возвести число в дробную степень
Проиллюстрируем на примере.
Решение
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Решение
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Вычислите приближенное значение 2 в степени 1,174367.
Решение