что такое доверительный интервал в статистике
Доверительные интервалы
Общий обзор
Взяв выборку из популяции, мы получим точечную оценку интересующего нас параметра и вычислим стандартную ошибку для того, чтобы указать точность оценки.
Однако, для большинства случаев стандартная ошибка как такова не приемлема. Гораздо полезнее объединить эту меру точности с интервальной оценкой для параметра популяции.
Это можно сделать, используя знания о теоретическом распределении вероятности выборочной статистики (параметра) для того, чтобы вычислить доверительный интервал (CI – Confidence Interval, ДИ – Доверительный интервал) для параметра.
Вообще, доверительный интервал расширяет оценки в обе стороны некоторой величиной, кратной стандартной ошибке (данного параметра); два значения (доверительные границы), определяющие интервал, обычно отделяют запятой и заключают в скобки.
Доверительный интервал для среднего
Использование нормального распределения
Выборочное среднее имеет нормальное распределение, если объем выборки большой, поэтому можно применить знания о нормальном распределении при рассмотрении выборочного среднего.
В частности, 95% распределения выборочных средних находится в пределах 1,96 стандартных отклонений (SD) среднего популяции.
Когда у нас есть только одна выборка, мы называем это стандартной ошибкой среднего (SEM) и вычисляем 95% доверительного интервала для среднего следующим образом:
Если повторить этот эксперимент несколько раз, то интервал будет содержать истинное среднее популяции в 95% случаев.
Обычно это доверительный интервал как, например, интервал значений, в пределах которого с доверительной вероятностью 95% находится истинное среднее популяции (генеральное среднее).
Хотя это не вполне строго (среднее в популяции есть фиксированное значение и поэтому не может иметь вероятность, отнесённую к нему) таким образом интерпретировать доверительный интервал, но концептуально это удобнее для понимания.
Использование t-распределения
Можно использовать нормальное распределение, если знать значение дисперсии в популяции. Кроме того, когда объем выборки небольшой, выборочное среднее отвечает нормальному распределению, если данные, лежащие в основе популяции, распределены нормально.
Если данные, лежащие в основе популяции, распределены ненормально и/или неизвестна генеральная дисперсия (дисперсия в популяции), выборочное среднее подчиняется t-распределению Стьюдента.
Вычисляем 95% доверительный интервал для генерального среднего в популяции следующим образом:
где — процентная точка (процентиль) t-распределения Стьюдента с (n-1) степенями свободы, которая даёт двухстороннюю вероятность 0,05.
Вообще, она обеспечивает более широкий интервал, чем при использовании нормального распределения, поскольку учитывает дополнительную неопределенность, которую вводят, оценивая стандартное отклонение популяции и/или из-за небольшого объёма выборки.
Когда объём выборки большой (порядка 100 и более), разница между двумя распределениями (t-Стьюдента и нормальным) незначительна. Тем не менее всегда используют t-распределение при вычислении доверительных интервалов, даже если объем выборки большой.
Обычно указывают 95% ДИ. Можно вычислить другие доверительные интервалы, например 99% ДИ для среднего.
Вместо произведения стандартной ошибки и табличного значения t-распределения, которое соответствует двусторонней вероятности 0,05, умножают её (стандартную ошибку) на значение, которое соответствует двусторонней вероятности 0,01. Это более широкий доверительный интервал, чем в случае 95%, поскольку он отражает увеличенное доверие к тому, что интервал действительно включает среднее популяции.
Доверительный интервал для пропорции
Выборочное распределение пропорций имеет биномиальное распределение. Однако если объём выборки n разумно большой, тогда выборочное распределение пропорции приблизительно нормально со средним .
Оцениваем выборочным отношением p=r/n (где r– количество индивидуумов в выборке с интересующими нас характерными особенностями), и стандартная ошибка оценивается:
95% доверительный интервал для пропорции оценивается:
Если объём выборки небольшой (обычно когда np или n(1-p) меньше 5), тогда необходимо использовать биномиальное распределение для того, чтобы вычислить точные доверительные интервалы.
Заметьте, что если p выражается в процентах, то (1-p) заменяют на (100-p).
Интерпретация доверительных интервалов
При интерпретации доверительного интервала нас интересуют следующие вопросы:
Насколько широк доверительный интервал?
Широкий доверительный интервал указывает на то, что оценка неточна; узкий указывает на точную оценку.
Ширина доверительного интервала зависит от размера стандартной ошибки, которая, в свою очередь, зависит от объёма выборки и при рассмотрении числовой переменной от изменчивости данных дают более широкие доверительные интервалы, чем исследования многочисленного набора данных немногих переменных.
Включает ли ДИ какие-либо значения, представляющие особенный интерес?
Можно проверить, ложится ли вероятное значение для параметра популяции в пределы доверительного интервала. Если да, то результаты согласуются с этим вероятным значением. Если нет, тогда маловероятно (для 95% доверительного интервала шанс почти 5%), что параметр имеет это значение.
Доверительные интервалы
Определение
Доверительные интервалы (англ. Confidence Intervals) одним из типов интервальных оценок используемых в статистике, которые рассчитываются для заданного уровня значимости. Они позволяют сделать утверждение, что истинное значение неизвестного статистического параметра генеральной совокупности находится в полученном диапазоне значений с вероятностью, которая задана выбранным уровнем статистической значимости.
Нормальное распределение
Когда известна вариация (σ 2 ) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.
Формула
Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула
где X – математическое ожидание выборки, α – уровень статистической значимости, Zα/2 – Z-оценка для уровня статистической значимости α/2, σ – среднеквадратическое отклонение генеральной совокупности, n – количество наблюдений в выборке. При этом, σ/√ n является стандартной ошибкой.
Таким образом, доверительный интервал для уровня статистической значимости α можно записать в виде
Пример
Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Zα/2=1,96. В этом случае нижняя и верхняя граница доверительного интервала составят
А сам доверительный интервал может быть записан в виде
Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.
Методы сужения доверительного интервала
Допустим, что диапазон [11,864; 18,136] является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.
Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Zα/2=1,64. В этом случае нижняя и верхняя граница интервала составят
А сам доверительный интервал может быть записан в виде
В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон [12,376; 17,624].
Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов
Сам доверительный интервал станет иметь следующий вид
Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.
Построение доверительного интервала при распределении отличном от нормального
В случае если среднеквадратичное отклонение генеральной совокупности не известно или распределение отлично от нормального, для построения доверительного интервала используется t-распределение. Это методика является более консервативной, что выражается в более широких доверительных интервалах, по сравнению с методикой, базирующейся на Z-оценке.
Формула
Для расчета нижнего и верхнего предела доверительного интервала на основании t-распределения применяются следующие формулы
где X – математическое ожидание выборки, α – уровень статистической значимости, tα – t-критерий Стьюдента для уровня статистической значимости α и количества степеней свободы (n-1), σ – среднеквадратическое отклонение выборки, n – количество наблюдений в выборке.
Сам доверительный интервал может быть записан в следующем виде
Распределение Стьюдента или t-распределение зависит только от одного параметра – количества степеней свободы, которое равно количеству индивидуальных значений признака (количество наблюдений в выборке). Значение t-критерия Стьюдента для заданного количества степеней свободы (n) и уровня статистической значимости α можно узнать из справочных таблиц.
Пример
Предположим, что размер выборки составляет 25 индивидуальных значений, математическое ожидание выборки равно 50, а среднеквадратическое отклонение выборки равно 28. Необходимо построить доверительный интервал для уровня статистической значимости α=5%.
В нашем случае количество степеней свободы равно 24 (25-1), следовательно соответствующее табличное значение t-критерия Стьюдента для уровня статистической значимости α=5% составляет 2,064. Следовательно, нижняя и верхняя граница доверительного интервала составят
А сам интервал может быть записан в виде
Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [38,442; 61,558].
Использование t-распределения позволяет сузить доверительный интервал либо за счет снижения статистической значимости, либо за счет увеличения размера выборки.
Снизив статистическую значимость с 95% до 90% в условиях нашего примера мы получим соответствующее табличное значение t-критерия Стьюдента 1,711.
В этом случае мы можем утверждать, что с вероятностью 90% математическое ожидание генеральной совокупности окажется в диапазоне [40,418; 59,582].
Если мы не хотим снижать статистическую значимость, то единственной альтернативой будет увеличение объема выборки. Допустим, что он составляет 64 индивидуальных наблюдения, а не 25 как в первоначальном условии примера. Табличное значение t-критерия Стьюдента для 63 степеней свободы (64-1) и уровня статистической значимости α=5% составляет 1,998.
Это дает нам возможность утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [43,007; 56,993].
Выборки большого объема
К выборкам большого объема относятся выборки из генеральной совокупности данных, количество индивидуальных наблюдений в которых превышает 100. Статистические исследования показали, что выборки большего объема имеют тенденцию быть нормально распределенными, даже если распределение генеральной совокупности отличается от нормального. Кроме того, для таких выборок применение z-оценки и t-распределения дают примерно одинаковые результаты при построении доверительных интервалов. Таким образом, для выборок большого объема допускается применение z-оценки для нормального распределения вместо t-распределения.
Подведем итоги
В таблице собраны рекомендации по выбору методики построения доверительных интервалов для различных ситуаций.
Доверительный интервал за 15 минут
Добрый день, уважаемые читатели!
Меня зовут Кирилл Мильчаков. Сегодня мы продолжаем наш разговор о биостатистике. Тема сегодняшней нашей беседы будет «Доверительный интервал». Что такое доверительный интервал? Вы наверняка встречались с ним в научной литературе. Доверительный интервал 95 %, либо сочетание символов ДИ и CI (confidence interval) 95 %. Что же означают эти 95 %? Какие он еще может принимать значения? И как его рассчитывать самостоятельно? Об этом обо всем сегодня мы и поговорим в этой статье.
Видео-версия статьи о доверительном интервале
Генеральная совокупность и выборочная совокупность
Прежде чем углубляться в тайны доверительного интервала, хотел бы вспомнить с вами 2 основных понятия статистической совокупности, с которыми чаще всего работают – это генеральная совокупность или выборочная совокупность или выборка.
Генеральная совокупность – это тот массив данных, о которых вы хотите сделать выводы.
Выборка является частью генеральной совокупности, которая участвует непосредственно в вашем эксперименте. Есть такое понятие как репрезентативность, сегодня мы не будем его касаться, главное запомнить, что выборка должна быть репрезентативной.
Если привести небольшой пример относительно генеральной совокупности и выборки, то можно вспомнить о простом случае из вашей жизни. Когда вы хотите узнать, достаточно ли посолен суп, вы берете ложку супа и пробуете его. Вам необязательно есть весь суп, чтобы понять, насколько он посолен. Ложка в данном случае является выборкой, по которой вы делаете вывод обо всей кастрюле супа. В данном случае кастрюля супа является генеральной совокупностью, а ложка супа является выборкой.
Итак, мы вспомнили с вами о 2 ключевых статистических совокупностях – о генеральной совокупности и выборочной совокупности. Теперь нужно вспомнить, что типы исследования, которые проводятся над генеральной совокупностью и выборочной совокупностью, называют по-разному. Над генеральной совокупностью проводятся так называемые сплошные исследования, над выборочной совокупностью – выборочные.
Теперь вспомним небольшие отличия между параметрами этих 2 совокупностей. Сегодня для того, чтобы понять, что такое доверительный интервал, нам понадобятся следующие вещи: во-первых, отличие средней арифметической в генеральной совокупности и в выборочной совокупности. В генеральной совокупности она имеет значок µ (мю), в выборочной – это x̅ (х с чертой) — это средние арифметические по каждому виду совокупности.
Далее нужно знать, что стандартное отклонение имеет значок выборочной – либо S, либо SD (standard deviation), а в случае генеральной совокупности оно носит название среднеквадратичного отклонения и обозначается буквой σ (сигма).
Приведем пример расчета доврительного интервала
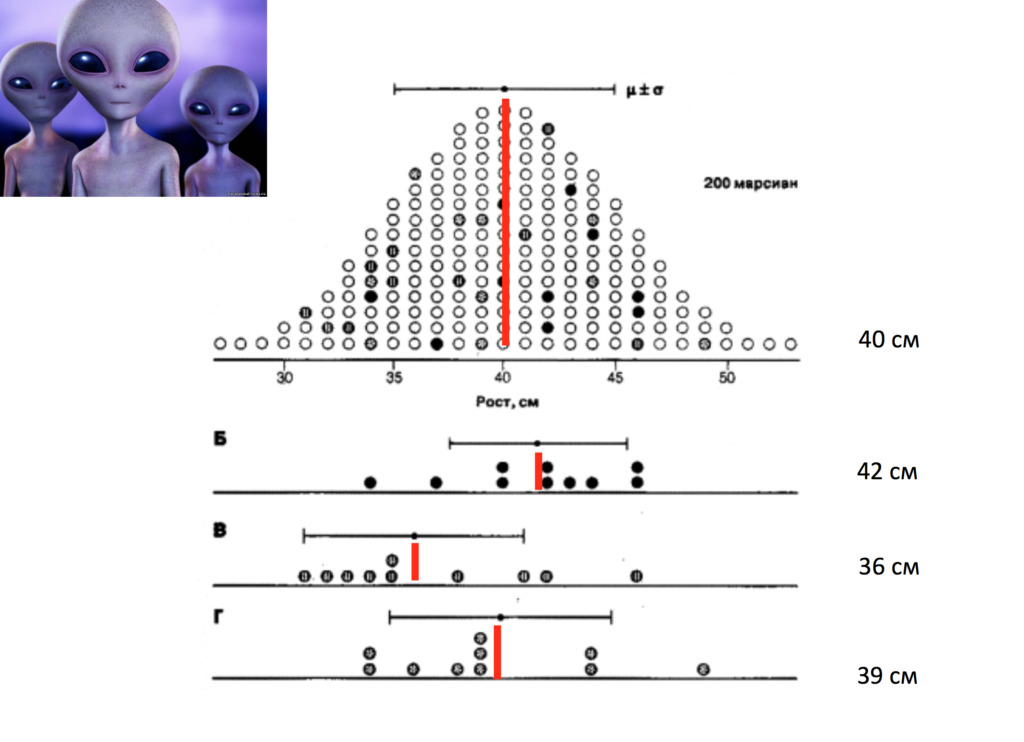
Представьте чисто гипотетическую ситуацию, когда перед нами стоит задача исследований среднего роста марсианина. Для того, чтобы его узнать, было отправлено 3 экспедиции. Первой из них повезло больше всего: они смогли поймать каждого из 200 марсианин и померить его рост.
Как мы помним, по закону нормального распределения по оси Х находится величина изучаемого признака, либо варианта (в данном случае это рост в сантиметрах), а по оси Y – частота встречаемости какого-то признака (мы его обозначаем буквой П.
Итак, оказалось, что у всех 200 марсиан средний рост составил 40 сантиметров. Таким образом, первая экспедиция смогла провести так называемое сплошное исследование, так как поработала со всеми единицами наблюдения генеральной совокупности. Поэтому мы имеем право назвать этот параметр µ.
Однако, второй и третьей экспедиции повезло гораздо меньше. Они попали в самые плохо населенные участки Марса и смогли отобрать только 10 марсиан. В данном случае оказалось, что средний рост по их выборке составил всего 38 сантиметров в первом случае и 41 сантиметр во втором случае.
Что же делать? Да, у нас есть данные из самого полного исследования, которое относится к первой экспедиции. Но представьте, что ни одна бы из них не смогла бы поработать со всей совокупностью полностью, и у нас были бы данные только от второй и третьей экспедиции. Что же в этой ситуации делать? Видно, что никто 40 сантиметров в действительности не достиг: во второй экспедиции Б она равна 38 сантиметрам, а в экспедиции В – 41 сантиметр. То есть в реальности никто не достиг 40 сантиметров. Что же делать в данном случае?
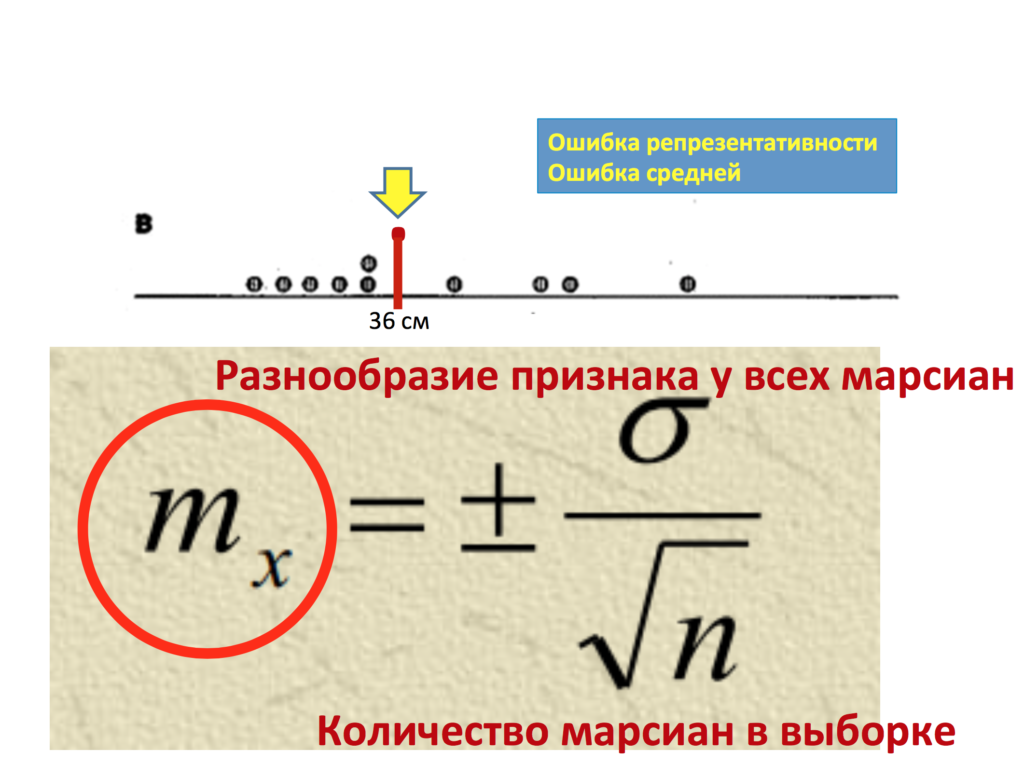
И вот здесь на помощь к нам приходит доверительный интервал, точнее оценка параметра. Доверительный интервал является вторым этапом оценки параметра. Прежде чем строить доверительный интервал, нам нужно понять, насколько в принципе этот параметр наша средняя (x̅б, x̅в) может отличаться, ошибаться от реального параметра в генеральной совокупности. Насколько?
Итак, предположим, мы нашли нашу ошибку репрезентативности mr. В данном случае она составила 2,7 сантиметра. Но что же это нам дает? А дает нам это уже достаточно много. Теперь мы, зная, насколько в принципе наша выборка может ошибаться относительно генеральной совокупности, можем составить определенное предположение о том, где же находится реальный параметр – реальные 40 сантиметров генеральной совокупности на основании данных лишь нашей выборки.
Для того, чтобы не залезать в критерий Стьюдента сегодня, я скажу лишь, что:
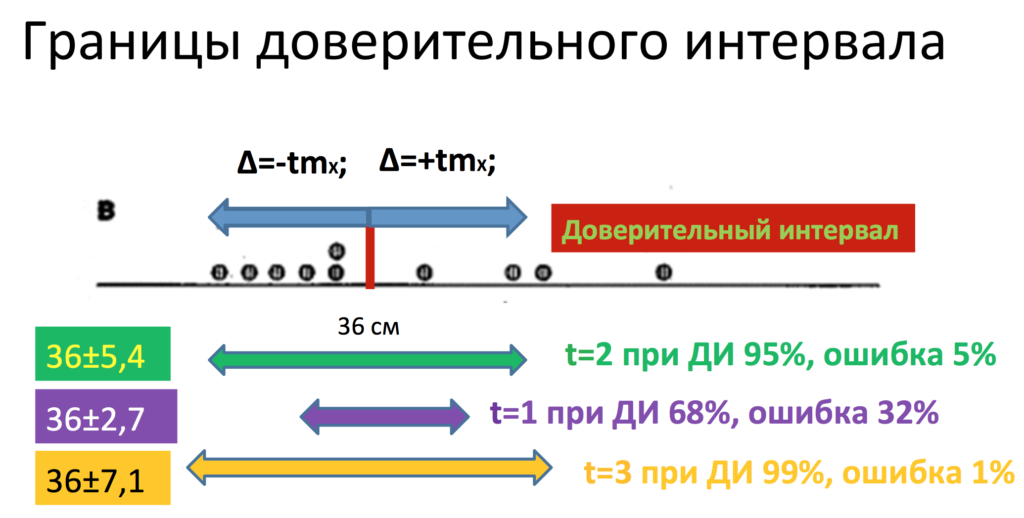
для доверительного интервала 95 % используется t=2,
для доверительного интервала 99 % используется t=3
и для доверительного интервала 68 % используется t=1.
Итак, после того, как мы нашли нашу предельную ошибку, мы можем построить доверительный интервал. Но для этого нам нужно самим задать тот доверительный интервал, который для нас подходит больше всего. Чаще всего в медицине используется вероятность ошибки 5 %, то есть доверительный интервал 95 % или вероятность ошибки 5 % (р=0,05, р=5 %).
Что же значат эти 95 %? А значат они следующее, что с 95%-ной вероятностью в нашем интервале лежит реальное значение, и лишь в 5 % случаев мы ошибаемся. То есть в нашем конкретном случае наша ошибка репрезентативности составила 2,7 сантиметра. Предельная ошибка отсюда будет равна чему? Именно 5,4 сантиметра, то есть доверительный интервал, так как здесь и плюс, и минус, то есть нам нужно ошибку умножить на 2, составил 10,8 сантиметров. А именно наши 38 см±5,4 см. Ширина всего доверительного интервала составляет 10,8 см. Напомню, что он складывается из положительной и отрицательной предельных ошибок вокруг нашей выборочной средней.
Итак, говоря о доверительном интервале, нужно сделать ряд важных выводов.
Если это видео оказалось Вам полезным, оно хотя бы немного раскрыло тайны доверительного интервала, ставьте лайки, подписывайтесь на наши рассылки и в комментариях пишите, какие темы по биостатистике вам бы были интересны для следующих выпусков. На этом я с вами прощаюсь. Меня зовут Кирилл. Пока!
Когда нам нужно получить одно число в качестве оценки параметра совокупности, мы используем точечную оценку. Тем не менее, из-за ошибки выборки, точечная оценка не будет в точности равняться параметру совокупности при любом размере данной выборки.
Часто, вместо точечной оценки, более полезным подходом будет найти диапазон значений, в рамках которого, как мы ожидаем, может находится значение искомого параметра с заданным уровнем вероятности.
Этот подход называется интервальной оценкой параметра (англ. ‘interval estimate of parameter’), а доверительный интервал выполняет роль этого диапазона значений.
Определение доверительного интервала.
Конечные значения доверительного интервала называются нижним и верхним доверительными пределами (или доверительными границами или предельной погрешностью, англ. ‘lower/upper confidence limits’).
Кроме того, можно определить два типа односторонних доверительных интервалов для параметра совокупности.
Нижний односторонний доверительный интервал устанавливает только нижний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности равен или превышает нижний предел.
Верхний односторонний доверительный интервал устанавливает только верхний предел. Это означает допущение, что с определенной степенью доверия параметр совокупности меньше или равен верхнему пределу.
Инвестиционные аналитики редко используют односторонние доверительные интервалы.
Доверительные интервалы часто дают либо вероятностную интерпретацию, либо практическую интерпретацию.
При вероятностной интерпретации, мы интерпретируем 95%-ный доверительный интервал для среднего значения совокупности следующим образом.
При повторяющейся выборке, 95% таких доверительных интервалов будут, в конечном счете, включать в себя среднее значение совокупности.
Например, предположим, что мы делаем выборку из совокупности 1000 раз, и на основании каждой выборки мы построим 95%-ный доверительный интервал, используя вычисленное выборочное среднее.
Из-за случайного характера выборок, эти доверительные интервалы отличаются друг от друга, но мы ожидаем, что 95% (или 950) этих интервалов включают неизвестное значение среднего по совокупности.
На практике мы обычно не делаем такие повторяющиеся выборки. Поэтому в практической интерпретации, мы утверждаем, что мы 95% уверены в том, что один 95%-ный доверительный интервал содержит среднее по совокупности.
Мы вправе сделать это заявление, потому что мы знаем, что 95% всех возможных доверительных интервалов, построенных аналогичным образом, будут содержать среднее по совокупности.
Доверительные интервалы, которые мы обсудим в этом чтении, имеют структуры, подобные описанной ниже базовой структуре.
Построение доверительных интервалов.
Точечная оценка \(\pm\) Фактор надежности \(\times\) Стандартная ошибка
Самый базовый доверительный интервал для среднего значения по совокупности появляется тогда, когда мы делаем выборку из нормального распределения с известной дисперсией. Фактор надежности в данном случае на основан стандартном нормальном распределении, которое имеет среднее значение, равное 0 и дисперсию 1.
Стандартная нормальная случайная величина обычно обозначается как \(Z\). Обозначение \(z_\alpha \) обозначает такую точку стандартного нормального распределения, в которой \(\alpha\) вероятности остается в правом хвосте.
Например, 0.05 или 5% возможных значений стандартной нормальной случайной величины больше, чем \( z_ <0.05>= 1.65 \).
Предположим, что мы хотим построить 95%-ный доверительный интервал для среднего по совокупности, и для этой цели, мы сделали выборку размером 100 из нормально распределенной совокупности с известной дисперсией \(\sigma^2\) = 400 (значит, \(\sigma\) = 20).
Мы рассчитываем выборочное среднее как \( \overline X = 25 \). Наша точечная оценка среднего по совокупности, таким образом, 25.
Если мы перемещаем 1.96 стандартных отклонений выше среднего значения нормального распределения, то 0.025 или 2.5% вероятности остается в правом хвосте. В силу симметрии нормального распределения, если мы перемещаем 1.96 стандартных отклонений ниже среднего, то 0.025 или 2.5% вероятности остается в левом хвосте.
В общей сложности, 0.05 или 5% вероятности лежит в двух хвостах и 0.95 или 95% вероятности лежит между ними.
Стандартная ошибка среднего значения выборки, заданная Формулой 1, равна \( \sigma_ <\overline X>= 20 \Big / \sqrt <100>= 2 \).
Верхний предел доверительного интервала равен \( \overline X + 1.96\sigma_ <\overline X>\) = 25 + 1.96(2) = 25 + 3.92 = 28.92.
95%-ный доверительный интервал для среднего по совокупности охватывает значения от 21.08 до 28.92.
Доверительные интервалы для среднего по совокупности (нормально распределенная совокупность с известной дисперсией).
Факторы надежности для наиболее часто используемых доверительных интервалов приведены ниже.
Факторы надежности для доверительных интервалов на основе стандартного нормального распределения.
Мы используем следующие факторы надежности при построении доверительных интервалов на основе стандартного нормального распределения:
На практике, большинство финансовых аналитиков используют значения для \(z_<0.05>\) и \(z_<0.005>\), округленные до двух знаков после запятой.
Для справки, более точными значениями для \(z_<0.05>\) и \(z_<0.005>\) являются 1.645 и 2.575, соответственно.
Для быстрого расчета 95%-ного доверительного интервала \(z_<0.025>\) иногда округляют 1.96 до 2.
Эти факторы надежности подчеркивают важный факт о всех доверительных интервалах. По мере того, как мы повышаем степень доверия, доверительный интервал становится все шире и дает нам менее точную информацию о величине, которую мы хотим оценить.
«Чем уверенней мы хотим быть, тем меньше мы должны быть уверены»
см. Freund и Williams (1977), стр. 266.
На практике, допущение о том, что выборочное распределение выборочного среднего, по меньшей мере, приблизительно нормальное, часто является обоснованным, либо потому, что исходное распределение приблизительно нормальное, либо потому что мы имеем большую выборку и поэтому к ней применима центральная предельная теорема.
Однако, на практике, мы редко знаем дисперсию совокупности. Когда дисперсия генеральной совокупности неизвестна, но выборочное среднее, по меньшей мере, приблизительно нормально распределено, у нас есть два приемлемых пути чтобы вычислить доверительные интервалы для среднего значения совокупности.
Вскоре мы обсудим более консервативный подход, который основан на t-распределении Стьюдента (t-распределение, для краткости).
В финансовой литературе, это наиболее часто используемый подход для статистической оценки и проверки статистических гипотез, касающихся среднего значения, когда дисперсия генеральной совокупности не известна, как для малого, так и для большого размер выборки.
В отличии от доверительного интервала, приведенного в Формуле 4, этот доверительный интервал использует стандартное отклонение выборки \(s\) при вычислении стандартной ошибки выборочного среднего (по Формуле 2).
Поскольку этот тип доверительного интервала применяется довольно часто, мы проиллюстрируем его вычисление в Примере 4.
Пример (4) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием z-статистики.
Предположим, что инвестиционный аналитик делает случайную выборку акций взаимных фондов США и рассчитывает средний коэффициент Шарпа.
Размер выборки равен 100, а средний коэффициент Шарпа составляет 0.45. Выборка имеет стандартное отклонение 0.30.
Рассчитайте и интерпретируйте 90-процентный доверительный интервал для среднего по совокупности всех акций взаимных фондов США с использованием фактора надежности на основе стандартного нормального распределения.
Фактор надежности для 90-процентного доверительного интервала, как указано ранее, составляет \( z_ <0.05>= 1.65 \).
Доверительный интервал будет равен:
Доверительный интервал охватывает значения 0.4005 до 0.4995, или от 0.40 до 0.50, с округлением до двух знаков после запятой. Аналитик может сказать с 90-процентной уверенностью, что интервал включает среднее по совокупности.
В этом примере аналитик не делает никаких конкретных предположений о распределении вероятностей, характеризующем совокупность. Скорее всего, аналитик опирается на центральную предельную теорему для получения приближенного нормального распределения для выборочного среднего.
Как показывает Пример 4, даже если мы не уверены в характере распределения совокупности, мы все еще можем построить доверительные интервалы для среднего по совокупности, если размер выборки достаточно большой, поскольку можем применить центральную предельную теорему.
Концепция степеней свободы.
Обратимся теперь к консервативной альтернативе и используем t-распределение Стьюдента, чтобы построить доверительные интервалы для среднего по совокупности, когда дисперсия генеральной совокупности не известна.
Для доверительных интервалов на основе выборок из нормально распределенных совокупностей с неизвестной дисперсией, теоретически правильный фактор надежности основан на t-распределении. Использование фактора надежности, основанного на t-распределении, имеет важное значение для выборок небольшого размера.
Применение фактора надежности \(t\) уместно, когда дисперсия генеральной совокупности неизвестна, даже если у нас есть большая выборка и мы можем использовать центральную предельную теорему для обоснования использования фактора надежности \(z\). В этом случае большой выборки, t-распределение обеспечивает более консервативные (широкие) доверительные интервалы.
t-распределение является симметричным распределением вероятностей и определяется одним параметром, известным как степени свободы (DF, от англ. ‘degrees of freedom’). Каждое значение для числа степеней свободы определяет одно распределение в этом семействе распределений.
Далее мы сравним t-распределения со стандартным нормальным распределением, но сначала мы должны понять концепцию степеней свободы. Мы можем сделать это путем изучения расчета выборочной дисперсии.
Каким образом использование выборочного среднего влияет на количество наблюдений, отобранных независимо, для формулы выборочной дисперсии?
При выборке размера 10 и среднем значении в 10%, к примеру, мы можем свободно отобрать только 9 наблюдений. Независимо от отобранных 9 наблюдений, мы всегда можем найти значение для 10-го наблюдения, которое дает среднее значение, равное 10%. С точки зрения формулы выборочной дисперсии, здесь есть 9 степеней свободы.
Концепция степеней свободы часто применяется в финансовой статистике, и вы встретите ее в последующих чтениях.
t-распределение Стьюдента.
Предположим, что мы делаем выборку из нормального распределения.
Коэффициент \(t\) не является нормальным, поскольку представляет собой отношение двух случайных величин, выборочного среднего и стандартного отклонения выборки.
Определение стандартной нормальной случайной величины включает в себя только одну случайную величину, выборочное среднее. По мере увеличения степеней свободы, однако, t-распределение приближается к стандартному нормальному распределению.
На Рисунке 1 показано стандартное нормальное распределение и два t-распределения, одно с DF = 2 и одно с DF = 8.
Из трех распределений, показанных на Рисунке 1, стандартное нормальное распределение имеет хвосты, которые стремятся к нулю быстрее, чем хвосты двух t-распределений. t-распределение симметрично распределено вокруг среднего нулевого значения, так же как и нормальное распределение.
По мере увеличения степеней свободы, t-распределение приближается к стандартному нормальному распределению. t-распределение с DF = 8 ближе к стандартному нормальному, чем t-распределение с DF = 2.
Помимо области плюс и минус четырех стандартных отклонений от среднего значения, остальная область под стандартным нормальным распределением, как представляется, близка к 0. Однако, оба t-распределения содержать некоторую площадь под каждой кривой за пределом четырех стандартных отклонений.
t-распределения имеют более толстые хвосты, но хвосты t-распределения Стьюдента с DF = 8 сильнее напоминают хвосты нормального распределения. По мере увеличения степеней свободы, хвосты распределения Стьюдента становятся менее толстыми.
Для часто используемых значений распределения Стьюдента составлены таблицы. Например, для каждой степени свободы \(t_<0.10>\), \(t_<0.05>\), \(t_<0.025>\), \(t_<0.01>\) и \(t_<0.005>\) значения будут такими, что соответственно, 0.10, 0.05, 0.025, 0.01 и 0.005 вероятности останется в правом хвосте для заданного числа степеней свободы.
Например, для DF = 30,
Приведем форму доверительных интервалов для среднего по совокупности, используя распределение Стьюдента.
Если мы делаем выборку из генеральной совокупности с неизвестной дисперсией и соблюдается одно из перечисленных ниже условий:
Пример 5 использует данные Примера 4, но применяет t-статистику, а не z-статистику, чтобы рассчитать доверительный интервал для среднего значения совокупности коэффициентов Шарпа.
Пример (5) расчета доверительного интервала для среднего по совокупности коэффициентов Шарпа с использованием t-статистики.
Как и в Примере 4, инвестиционный аналитик стремится вычислить 90-процентный доверительный интервал для среднего по совокупности коэффициентов Шарпа, основанных на случайной выборке из 100 взаимных фондов США.
Теперь, признав, что дисперсия генеральной совокупности распределения коэффициентов Шарпа неизвестна, аналитик решает вычислить доверительный интервал, используя теоретически правильную t-статистику.
Поскольку размер выборки равен 100, DF = 99. Используя таблицу степеней свободы, мы находим, что \(t_<0.05>\) = 1.66.
Этот фактор надежности немного больше, чем фактор надежности \(z_<0.05>\) = 1.65, который был использован в Примере 4.
Доверительный интервал будет:
Доверительный интервал охватывает значения 0.4002 до 0.4998, или 0.40 до 0.50, с двумя знаками после запятой. При округлении до двух знаков после запятой, доверительный интервал не изменился по сравнению с Примером 4.
В Таблице 3 приведены различные факторы надежности, которые мы использовали.