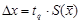что такое доверительный интервал в метрологии
Доверительные интервалы
Приведенные выше оценки параметров распределения случайных величин в виде среднего арифметического для оценки математического ожидания и СКО для оценки дисперсии называются точечными оценками, так как они выражаются одним числом. Однако в некоторых случаях знание точечной оценки является недостаточным. Наиболее корректной и наглядной оценкой случайной погрешности измерений является оценка с помощью доверительных интервалов.
Симметричный интервал в границами ± Δх(Р) называется доверительным интервалом случайной погрешности с довери-тельной вероятностью Р, если площадь кривой распределения между абсциссами –Δх и +Δх составляет Р-ю часть всей площади под кривой плотности распределения вероятностей. При нормировке всей площади на единицу Р представляет часть этой площади в долях единицы (или в процентах). Другими словами, в интервале от -Dх(Р) до +Dх(Р) с заданной вероятностью Р встречаются Р×100% всех возможных значений случайной погрешности.
Доверительный интервал для нормального распределения находится по формуле:
где коэффициент t зависит от доверительной вероятности Р.
Для нормального распределения существуют следующие соотношения между доверительными интервалами и доверительной вероятностью: 1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999).
Доверительные вероятности для выражения результатов измерений и погрешностей в различных областях науки и техники принимаются равными. Так, в технических измерениях принята доверительная вероятность 0,95. Лишь для особо точных и ответственных измерений принимают более высокие доверительные вероятности. В метрологии используют, как правило, доверитель-ные вероятности 0,97, в исключительных случаях 0,99. Необходимо отметить, что точность измерений должна соответствовать поставленной измерительной задаче. Излишняя точность ведет к неоправданному расходу средств. Недостаточная точность измерений может привести к принятию по его результатам ошибочных решений с самыми непредсказуемыми последствиями, вплоть до серьезных материальных потерь или катастроф.
При проведении многократных измерений величины х, подчиняющейся нормальному распределению, доверительный интервал может быть построен для любой доверительной вероятности по формуле:
где tq – коэффициент Стьюдента, зависящий от числа наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью таблицы q-процентных точек распределения Стьюдента, которая имеет два параметра: k = n – 1 и q = 1 – P;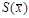 
– оценка среднего квадратического отклонения среднего арифметического.
Доверительный интервал для погрешности Dх(Р) позволяет построить доверительный интервал для истинного (действи-тельного) значения измеряемой величины , оценкой которой является среднее арифметическое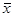 
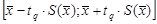
. Истинное значение измеряе-мой величины находится с доверительной вероятностью Р внутри интервала: 
. Доверительный интервал позволяет выяснить, насколько может измениться полученная в результате данной серии измерений оценка измеряемой величины при проведении повторной серии измерений в тех же условиях. Необходимо отметить, что доверительные интервалы строят для неслучайных величин, значения которых неизвестны. Такими являются истинное значение измеряемой величины и средние квадратические отклонения. В то же время оценки этих величин, получаемые в результате обработки данных наблюдений, являются случайными величинами.
Недостатком доверительных интервалов при оценке случай-ных погрешностей является то, что при произвольно выбираемых доверительных вероятностях нельзя суммировать несколько погреш-ностей, т.к. доверительный интервал суммы не равен сумме довери-тельных интервалов. Суммируются дисперсии независимых случай-ных величин: Då = åDi. То есть, для возможности суммирования составляющие случайной погрешности должны быть представлены своими СКО, а не предельными или доверительными погрешностя-ми.
6.5. доверительная вероятность и доверительный интервал
6.5. доверительная вероятность и доверительный интервал
Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной дове рителъной вероятностью
где q — уровень значимости; хн, хв— нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра.
В общем случае доверительные интервалы можно строить на основе неравенства Чебышева. При любом законе распределения случайной величины, обладающей моментами первых двух порядков, верхняя граница вероятности попадания отклонения случайной величины х от центра распределения Хц в интервал tSx описывается неравенством Чебышева
где Sx — оценка СКО распределения; t — положительное число.
Для нахождения доверительного интервала не требуется знать закон распределения результатов наблюдений, но нужно знать оценку СКО. Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверительной вероятности 0,9 для многих законов распределений соответствует доверительный интервал 1,6SX. Неравенство Чебышева дает в данном случае 3,16SX. В связи с этим оно не получило широкого распространения.
В метрологической практике используют главным образом кван-тильные оценки доверительного интервала. Под 100P-процентным квантилем хр понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р\%. Иначе говоря, квантиль — это значение случайной величины (погрешности) с заданной доверительной вероятностью Р. Например, медиана распределения является 50\%-ным квантилем х0,5.
На практике 25и 75\%-ный квантили принято называть сгибами, или квантилями распределения. Между ними заключено 50\% всех возможных значений случайной величины, а остальные 50\% лежат вне их. Интервал значений случайной величины х между х0 05 и х0 95 охватывает 90\% всех ее возможных значений и называется интерквантильным промежутком с 90\%-ной вероятностью. Его протяженность равна d0,9= х0,95 х0,05.
На основании такого подхода вводится понятие квантильных значений погрешности, т.е. значений погрешности с заданной доверительной вероятностью Р — границ интервала неопределенности ± DД = ± (хр х1-р)/2 = ± dp/2. На его протяженности встречается Р\% значений случайной величины (погрешности), a q = (1Р)\% общего их числа остаются за пределами этого интервала.
Для получения интервальной оценки нормально распределенной случайной величины необходимо:
• определить точечную оценку МО х̅ и СКО Sx случайной величины по формулам (6.8) и (6.11) соответственно;
• выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99;
• найти верхнюю хв и нижнюю хн границы в соответствии с уравнениями
полученными с учетом (6.1). Значения хн и хв определяются из таблиц значений интегральной функции распределения F(t) или функции Лапласа Ф(1).
Полученный доверительный интервал удовлетворяет условию
(6.13)
где n — число измеренных значений; zp — аргумент функции Лапласа Ф(1), отвечающей вероятности Р/2. В данном случае zp называется квантильным множителем. Половина длины доверительного интервала 
называется доверительной границей погрешности результата измерений.
Пример 6.1. Произведено 50 измерений постоянного сопротивления. Определить доверительный интервал для МО значения постоянного сопротивления, если закон распределения нормальный с параметрами mx = R = 590 Ом, Sx= 90 Ом при доверительной вероятности Р = 0,9.
Так как гипотеза о нормальности закона распределения не противоречит опытным данным, доверительный интервал определяется по формуле
Отсюда Ф(zр) = 0,45. Из таблицы, приведенной в приложении 1, находим, что zp= 1,65. Следовательно, доверительный интервал запишется в виде
или 590 21 Предмет: Физика Автор: Сергеев Алексей Георгиевич Год издания: 2001 Язык учебника: русский Рейтинг: 
Просмотров: 9412
Что такое доверительный интервал в метрологии
ГОСТ Р 50779.22- 2005
(ИСО 2602:1980)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Точечная оценка и доверительный интервал для среднего
Дата введения 2005-07-01
Задачи, основные принципы и правила проведения работ по государственной стандартизации в Российской Федерации установлены ГОСТ Р 1.0-92 «Государственная система стандартизации Российской Федерации. Основные положения» и ГОСТ Р 1.2-92 «Государственная система стандартизации Российской Федерации. Порядок разработки государственных стандартов»
Сведения о стандарте
1 ПОДГОТОВЛЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» и Научно-исследовательским центром контроля и диагностики технических систем на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением технического регулирования и стандартизации Федерального агентства по техническому регулированию и метрологии
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ 1.5 (подраздел 3.6)
1 Область применения
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 50779.10.
4 Условия применения методов
Результаты испытаний представлены результатами измерений непрерывной величины. Настоящий стандарт не охватывает обработку результатов испытаний, когда исследуемая величина является дискретной (например, наличие или отсутствие свойства, количество дефектов).
Предположение о нормальности очень широко используют: распределение результатов, полученных в условиях испытаний, обычно нормальное или почти нормальное распределение.
Может быть, однако, полезным проверить предположение о нормальности распределения с помощью соответствующих методов. Вычисления могут быть упрощены изменением начала координат или единицы измерения результатов испытаний, но округлять эти результаты не рекомендуется. Недопустимо отбрасывать любые результаты наблюдений или применять любые корректировки к очевидно неопределенным наблюдениям, не подкрепленные доказательствами на экспериментальной, технической или какой-либо другой основе, которая должна быть четко установлена.
Метод испытаний может быть источником систематических ошибок, которые в настоящем стандарте не определены. Однако существование таких ошибок может сделать неприменимыми методы, изложенные далее.
В частности, если имеет место несистематическое смещение, увеличение выборки размера не повлияет на смещение.
Методы, представленные в ГОСТ Р 50779.21, могут быть использованы в определенных случаях для идентификации систематических ошибок.
5 Точечная оценка среднего
5.1 Случай несгруппированных результатов
Среднее основного нормального распределения оценивают как среднее арифметическое результатов:
. (1)
5.2 Случай сгруппированных в классы результатов
Когда число результатов достаточно велико (например, более 50), может быть выгодно сгруппировать их в классы одинаковой ширины. В определенных случаях результаты могут быть получены уже сгруппированными в классы.
. (2)
. (3)
6 Доверительный интервал для среднего
Доверительный интервал для среднего совокупности вычисляют на основе оценок среднего и стандартного отклонения.
Альтернативный метод вычисления доверительного интервала с использованием размахов дан в приложении А.
6.1 Оценка стандартного отклонения
6.1.1 Случай несгруппированных результатов
, (4)
— общее число измерений;
— среднее арифметическое измерений, вычисленное по формуле (1).
Для упрощения вычислений рекомендуется использовать формулу
. (5)
6.1.2 Случай сгруппированных результатов
В случае группирования в классы формула для оценки стандартного отклонения имеет вид
, (6)
— общее число измерений;
— взвешенное среднее всех средних точек классов, вычисленное по формуле (3).
Для простоты вычислений рекомендуется использовать формулу
. (7)
В случае сгруппированных данных вычисленное значение может быть скорректировано (поправка Шеппарда). Поскольку эта поправка при правильно выбранной ширине класса невелика, ее вводят не всегда.
6.2 Доверительный интервал для среднего
Доверительный интервал определяется тем, какая выбрана доверительная вероятность (0,95 или 0,99), и тем, какой будет построен интервал (односторонний или двусторонний).
6.2.1 Двусторонний доверительный интервал
Двусторонний доверительный интервал для среднего совокупности определяют по следующим формулам:
а) для доверительной вероятности 0,95:
; (8)
б) для доверительной вероятности 0,99:
. (9)
Что такое доверительный интервал в метрологии
Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров.
Половина длины доверительного интервала называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р=0.95 или Р=0.995 и по формулам
Полученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.
Половина длины нового доверительного интервала
называется доверительной границей погрешности результата измерений, а итог измерений записывается в виде
Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих условиях пользуются отношением
Плотность распределения этой дроби, впервые предсказанного Госсетом, писавшим под псевдонимом Стьюдент, выражается следующим уравнением:
или, поскольку S(t, k) является четной функцией аргумента t,
Пример. По результатам пяти наблюдений была найдена длина стержня. Итог измерений составляет L=15.785 мм, =0.005 мм, причем существуют достаточно обоснованные предположения о том, что распределение результатов наблюдений было нормальным. Требуется оценить вероятность того, что истинное значение длины стержня отличается от среднего арифметического из пяти наблюдений не больше чем на 0.01 мм.
Из условия задачи следует, что имеются все основания для применения распределения Стьюдента.
Вычисляем значение дроби Стьюдента
и число степеней свободы
.
По данным табл.П.4 приложения находим значение доверительной вероятности для
Для =3 вероятность составляет
т.е несколько меньше 0.9973, как при нормальном распределении. Итог измерений удобно записать в виде
Для =1 доверительная вероятность составляет приблизительно 0.62, поэтому итог измерений можно представить также в виде
В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной.
Кроме того, на основании центральной предельной теоремы теории вероятностей можно утверждать, что при достаточно большом числе наблюдений распределение среднего арифметического как суммы случайных величин будет сколь угодно близким к нормальному. Тогда, заменяя дисперсию ее точечной оцен-кой [см.п.4.4. Нормальное распределение], можно для оценки доверительной гра-ницы погрешности результата воспользоваться равенством (35). Число наблюдений n, при котором это становится возможным, зависит, конечно, от распределения случайных погрешностей.
Соотношения (38) показывают, что итог измерения не есть одно определенное число. В результате измерений мы получаем лишь полосу значений измеряемой величины. Смысл итога измерений, например, L=20.00±0.05 заключается не в том, что L = 20.00, как для простоты счи-тают, а в том, что истинное значение лежит где-то в границах от 19.95 до 20.05. К тому же нахождение внутри границ имеет некоторую вероятность, меньшую, чем единица, и, следовательно, нахождение вне границ не исключено, хотя и может быть очень маловероятным.
Теперь найдем доверительные интервалы для дисперсии и среднеквадратического отклонения результатов наблюдений.
Если распределение результатов наблюдений нормально, то отношение
Пользуясь этой таблицей, можно найти доверительный интервал для оценки дисперсии результатов наблюдений при заданной доверительной вероятности. Этот интервал строится таким образом, чтобы вероятность выхода дисперсии за его границы не превышала некоторой малой величины q, причем вероятности выхода за обе границы интервала были бы равны между собой и составляли соответственно q/2 (рис.10).
Границы и такого доверительного интервала находят из равенства
Полученное равенство означает, что с вероятностью истинное значение среднеквадратического отклонения результатов наблюдений лежит в интервале ( ], границы которого равны
Пример. Даны результаты двадцати измерений длины мм детали (табл.3).