что такое допуск в метрологии

Метрология

Допуски и посадки

Основные понятия о допусках и посадках

Производственный опыт показал, что задачу выбора оптимальной точности можно решить установлением для каждого размера детали (особенно для сопрягаемых ее размеров) пределов, в которых может колебаться ее действительный размер; при этом исходят из того, что узел, в который входит деталь, должен соответствовать своему назначению и не терять работоспособность в требуемых условиях функционирования с необходимым ресурсом.

Номинальным называют основной размер, получаемый из расчета на прочность, жесткость или выбираемый конструктивно и проставляемый на чертеже. Проще говоря, номинальный размер детали получен конструкторами и разработчиками расчетным путем (исходя из требований прочности, жесткости и т. п.) и указывается на чертеже детали в виде основного размера.
Номинальный размер соединения является общим для отверстия и вала, составляющих соединение. По номинальным размерам выполняют в том или ином масштабе чертежи деталей, сборочных единиц и приборов.

Посадки

Действительный зазор будет находиться между указанными пределами, т. е. между максимальным и минимальным зазором. Зазор необходим для обеспечения подвижности соединения и размещения смазки. Чем выше число оборотов и выше вязкость смазки, тем больше должен быть зазор.

В посадках с натягом так выбирают предельные размеры вала и отверстия, чтобы в сопряжении был гарантированный натяг, ограниченный минимальным и максимальным значениями – Nmax и Nmin :

Посадки в системе отверстия и системе вала

Посадки, установленные ЕСДП СЭВ, могут быть осуществлены по системам отверстия или вала.

На промышленных предприятиях в основном применяют систему отверстия, так как она требует меньшего количества режущего и измерительного инструмента, т. е. более экономична. Кроме того, технологически удобнее подгонять вал под отверстие, а не наоборот, поскольку удобнее производить обработку и контрольные измерения внешней поверхности, а не внутренней.
Систему вала, как правило, применяют для наружных колец шарикоподшипников и в тех случаях, когда на гладкий вал насаживают несколько деталей с различными посадками.

Квалитеты

В системе СЭВ для обозначения допусков с указанием квалитетов применяются следующие условные обозначения:

Графическое изображение допусков и посадок

Построение выполняется следующим образом.
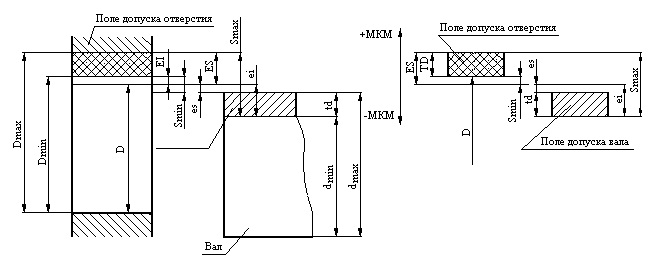
От горизонтальной линии, условно изображающей поверхность детали при ее номинальном размере, откладывают предельные отклонения в произвольно выбранном масштабе. Обычно на схемах величины отклонений указывают в микронах, но можно строить поля допусков и в миллиметрах, если отклонения достаточно большие.

На схемах указывают номинальный D и предельные ( Dmax, Dmin, dmax, dmin ) размеры, предельные отклонения ( ES, EI, es, ei ) поля допусков и другие параметры.

Использование всех основных отклонений и квалитетов позволяет получить 490 полей допусков для валов и 489 для отверстий. Такие широкие возможности образования полей допусков позволяют применять ЕСДП в различных специальных случаях. Это является ее существенным достоинством. Однако на практике использование всех полей допусков неэкономично, так как вызовет чрезмерное разнообразие посадок и специальной технологической оснастки.

При разработке национальных систем допусков и посадок на базе систем ИСО из всего многообразия полей допусков отбирают только те поля, которые обеспечивают потребности промышленности страны и ее внешнеэкономические связи.

Поле допуска в ЕСДП СЭВ образуется сочетанием одного из основных отклонений с допуском по одному из квалитетов. В соответствии с этим поле допуска обозначается буквой основного отклонения и номером квалитета, например 65f6; 65e11 — для вала; 65Р6; 65H7 — для отверстия.
Основные отклонения зависят от номинальных размеров деталей и остаются постоянными для всех квалитетов. Исключение составляют основные отклонения отверстий J, К, М, N и валов j и k, которые при одинаковых номинальных размерах, в разных квалитетах имеют различные значения. Поэтому на схемах поля допусков с отклонениями J, К, М, N, j, k, обычно разделены на части и показаны ступенчатыми.

Специфичны поля допусков типа js6, Js8, Js9 и т.д. Они фактически не имеют основного отклонения, поскольку расположены симметрично относительно нулевой линии. По определению основное отклонение – это отклонение ближайшее к нулевой линии. Значит, оба отклонения таких специфических полей допусков могут быть признаны основными, что недопустимо.

Допуски и посадки установлены для четырех диапазонов номинальных размеров:

Средний диапазон является наиболее важным, поскольку применяется значительно чаще.

Обозначение допусков на чертежах

Указания и обозначения на чертежах предельных отклонений формы и расположения поверхностей регламентируются ГОСТ 2.308-79, который предусматривает для этих целей специальные знаки и символы.
С основными положениями этого стандарта, используемыми знаками и символами для обозначения предельных отклонений, можно ознакомиться в этом документе (формат WORD, 400 кБ).

Источник

Что такое допуск в метрологии

Limits and fits. Basic definitions

Дата введения 1963-01-01

1. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Комитетом стандартов, мер и измерительных приборов при Совете Министров СССР 26.03.62

3. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ

Обозначение НТД, на который дана ссылка

Номер пункта, приложения

4. Ограничение срока действия снято Постановлением Госстандарта СССР от 16.07.80 N 3626

5. ИЗДАНИЕ с Изменениями N 2, 3, утвержденными в мае 1970 г., июле 1980 г., (ИУС 5-70, 9-80)

1. Настоящий стандарт распространяется на гладкие цилиндрические соединения и плоские соединения с параллельными плоскостями* и устанавливает основные определения для системы допусков и посадок ОСТ, определяемой следующими стандартами: ГОСТ 11472, ГОСТ 8809, ГОСТ 3047, ОСТ НКМ 1011, ОСТ НКМ 1041, ОСТ 1012, ОСТ 1042, ОСТ 1043, ОСТ 1044, ОСТ НКМ 1016, ОСТ 1013, ОСТ 1069, ОСТ НКМ 1017, ОСТ 1014, ОСТ 1015, ОСТ НКМ 1021, ОСТ 1022, ОСТ 1142, ОСТ 1143, ОСТ НКМ 1026, ОСТ 1023, ОСТ НКМ 1027, ОСТ 1024, ОСТ 1025, ОСТ 1010, ГОСТ 2689, ГОСТ 11710.

* Применение стандарта для вновь разрабатываемых изделий не допускается.

1. Предельные отклонения и допуски, устанавливаемые стандартами на допуски и посадки, относятся к деталям, размеры которых определены при нормальной температуре 20 °С по ГОСТ 9249.

(Измененная редакция, Изм. N 3).

Примечание. Названия «отверстие» и «вал» условно применимы также и к другим охватывающим и охватываемым поверхностям.

3. Номинальным размером называется основной размер, определенный исходя из функционального назначения детали и служащий началом отсчета отклонений. Общий для отверстия и вала, составляющих соединение, номинальный размер называется номинальным размером соединения.

2. Номинальные размеры должны выбираться по ГОСТ 6636.

4. Действительным размером называется размер, полученный в результате измерения с допустимой погрешностью.

Примечание. Предельными размерами ограничиваются действительные размеры годных деталей, полученные измерением с допустимой погрешностью. Случаи, когда предельными размерами должны ограничиваться действительные размеры с учетом погрешностей измерения, следует оговаривать особо.

6. Отклонением размера называется алгебраическая разность между размером и его номинальным значением. Отклонение является положительным, если размер больше номинального, и отрицательным, если размер меньше номинального.

Действительным отклонением называется алгебраическая разность между действительным и номинальным размерами.

7. Допуском размера называется разность между наибольшим и наименьшим предельными размерами.

9. Полем допуска называется интервал значений размеров, ограниченный предельными размерами; оно определяется величиной допуска и его расположением относительно номинального размера. На схеме поле допуска изображается зоной между линиями, соответствующими верхнему и нижнему предельным отклонениям.

10. Размеры поверхности считаются находящимися в поле допуска, если в поле допуска находятся как измеренные двухточечным методом размеры проверяемой детали в любом месте поверхности, так и размеры геометрически правильного прототипа сопрягаемой детали, плотно (без зазора и натяга) сопрягающегося с проверяемой деталью.

Случаи, когда допускаются отступления от этого правила, должны быть оговорены особо.

Примечание. Приведенное в п.10 правило не предопределяет методику контроля.

11. Посадкой называется характер соединения деталей, определяемый величиной получающихся в нем зазоров или натягов. Посадка характеризует большую или меньшую свободу относительного перемещения соединяемых деталей или степень сопротивления их взаимному смещению.

12. Зазором называется положительная разность между размерами отверстия и вала (размер отверстия больше размера вала).

Натягом называется положительная разность между размерами вала и отверстия до сборки деталей (размер вала больше размера отверстия).

13. Посадки подразделяются на три группы:

а) посадки с зазором, при которых обеспечивается зазор в соединении;

б) посадки с натягом, при которых обеспечивается натяг в соединении;

в) переходные посадки, при которых возможно получение как натягов, так и зазоров.

Деление посадок по группам в стандартах на допуски и посадки производится в зависимости от взаимного расположения полей допусков отверстия и вала. К посадкам с зазором относятся посадки, в которых поле допуска отверстия расположено над полем допуска вала, в том числе и «скользящие» посадки, в которых нижняя граница поля допуска отверстия совпадает с верхней границей поля допуска вала.

К посадкам с натягом относятся посадки, в которых поле допуска вала расположено над полем допуска отверстия. К переходным посадкам относятся посадки, в которых поля допусков отверстия и вала перекрываются (черт.2).

14. Наибольшим и наименьшим зазором (или натягом) называются два предельных значения, между которыми должен находиться зазор (или натяг).

15. Допуском посадки называется разность между наибольшим и наименьшим зазорами (в посадках с зазором) или наибольшим и наименьшим натягом (в посадках с натягом).

В переходных посадках допуск посадки равен алгебраической разности между наибольшим и наименьшим натягами или сумме наибольшего натяга и наибольшего зазора.

16. Системой отверстия называется совокупность посадок, в которых предельные отклонения отверстий одинаковы (при одном и том же классе точности и одном и том же номинальном размере), а различные посадки достигаются путем изменения предельных отклонений валов (черт.3). Во всех стандартных посадках системы отверстия нижнее отклонение отверстий равно нулю. Такое отверстие называется основным отверстием.

Источник

Что такое допуск в метрологии

Основные нормы взаимозаменяемости

ЕДИНАЯ СИСТЕМА ДОПУСКОВ И ПОСАДОК

Общие положения, ряды допусков и основных отклонений

Basic norms of interchangeability. Unified system of tolerances and fits. General, series of tolerances and fundamental deviations

Дата введения 1990-01-01

1. РАЗРАБОТАН И ВНЕСЕН Министерством станкостроительной и инструментальной промышленности СССР

2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 11.04.89 N 983

3. ВЗАМЕН ГОСТ 25346-82

4. Стандарт полностью соответствует СТ СЭВ 145-88

5. Стандарт соответствует международному стандарту ИСО 286-1-88*

7. ИЗДАНИЕ с Поправками (ИУС 1-91, 5-92)

Настоящий стандарт распространяется на гладкие элементы деталей, цилиндрические и ограниченные параллельными плоскостями, а также на образованные ими посадки и устанавливает термины, определения и условные обозначения, допуски и основные отклонения системы допусков и посадок для размеров до 3150 мм и любых линейных размеров, если они не установлены другими стандартами.

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ

1.1. Термины и определения

Примечание. В дальнейшем в стандарте под термином «допуск» понимают «стандартный допуск».

Примечание. Применявшийся ранее термин «проходной предел» использовать не рекомендуется.

Примечание. Применявшийся ранее термин «непроходной предел» использовать не рекомендуется.

Примечание. Натяг можно определять как отрицательную разность между размерами отверстия и вала.

Источник

Что такое допуск в метрологии

Основные нормы взаимозаменяемости

ЕДИНАЯ СИСТЕМА ДОПУСКОВ И ПОСАДОК

Поля допусков и рекомендуемые посадки

Basic norms of interchangebility. Unified sistem of tolerances and fits. Tolerance zones and recommendalle fils*

Дата введения 1983-07-01

1. РАЗРАБОТАН И ВНЕСЕН Министерством станкостроительной и инструментальной промышленности СССР

2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 21.07.82 N 2764

3. Стандарт полностью соответствует СТ СЭВ 144-88

4. Стандарт соответствует международным стандартам ИСО 286-2-88*, ИСО 1829 в части отобранных полей допусков

5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ

Обозначение НТД, на который дана ссылка

6. ИЗДАНИЕ с Изменением N 1, утвержденным в октябре 1989 г. (ИУС 1-90)

Настоящий стандарт распространяется на гладкие элементы деталей с номинальными размерами до 3150 мм и устанавливает поля допусков для гладких деталей в посадках и для несопрягаемых элементов.

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Устанавливаемые настоящим стандартом поля допусков валов и отверстий являются ограничительным отбором для общего применения из всей совокупности полей допусков, которые могут быть получены различным сочетанием основных отклонений и допусков по ГОСТ 25346.

Поля допусков, не включенные в данный стандарт, являются специальными. Их применение допускается лишь в технически и экономически обоснованных случаях (если применение полей допусков по настоящему стандарту не обеспечивает требования, предъявляемые к изделиям) или если они предусмотрены в государственных стандартах для соответствующих видов продукции (изделий), материалов или способов изготовления.

1.2. Рекомендации по образованию посадок из предусмотренных в настоящем стандарте полей допусков валов и отверстий приведены в приложении 1.

2. ПОЛЯ ДОПУСКОВ ПРИ НОМИНАЛЬНЫХ РАЗМЕРАХ менее 1 мм

2.1. Поля допусков должны соответствовать указанным в табл.1 и 2.

2.2. Числовые значения предельных отклонений размеров должны соответствовать указанным в табл.3 и 4.

(Измененная редакция, Изм. N 1).

2.3. Рекомендуемые поля допусков валов и отверстий в интервалах номинальных размеров менее 1 мм приведены в приложении 2.

3. ПОЛЯ ДОПУСКОВ ПРИ НОМИНАЛЬНЫХ РАЗМЕРАХ от 1 до 500 мм

3.1. Поля допусков должны соответствовать указанным в табл.5 и 6. В первую очередь следует применять предпочтительные поля допусков (обозначение их заключено в утолщенные рамки).

3.2. Числовые значения предельных отклонений размеров должны соответствовать указанным в табл.7 и 8.

3.1, 3.2. (Измененная редакция, Изм. N 1).

3.3. В технически и экономически обоснованных случаях (если применение полей допусков по табл.5 и 6 не обеспечивает предъявляемых к изделиям требований) допускается применение дополнительных полей допусков, приведенных в приложении 3.

4. ПОЛЯ ДОПУСКОВ ПРИ НОМИНАЛЬНЫХ РАЗМЕРАХ свыше 500 до 3150 мм

4.1. Поля допусков должны соответствовать указанным в табл.9 и 10.

4.2. Числовые значения предельных отклонений размеров должны соответствовать указанным в табл.11 и 12.

4.1, 4.2. (Измененная редакция, Изм. N 1).

Поля допусков валов при номинальных размерах менее 1 мм

Источник

21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения.

21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения. 21. Основные понятия и определения по допускам и посадкам. Допуски, посадки и технические измерения.

Поверхности, размеры, отклонения и допуски. Поверхности деталей бывают сопрягаемыми и несопрягаемыми, или свободными. При этом они могут быть цилиндрическими, плоскими, коническими, эвольвентными, сложными (шлицевые, винтовые) и др. Со-прягаемыми называют поверхности, по которым детали соединяются в сборочные единицы, а сборочные единицы — в механизмы. Несопрягаемыми, или свободными, — конструктивно необходимые поверхности, не предназначенные для соединения с поверхностями других деталей.

Внутренние цилиндрические поверхности, а также внутренние поверхности с парал-лельными плоскостями (отверстия в ступицах, шпоночные пазы и пр.) являются охватывающими (их условно называют отверстиями; диаметры отверстий обозначают буквой D). Наружные отверстия (цилиндрическая поверхность вала, боковые грани шпонок) являются охватываемыми (их условно называют валами и обозначают буквой d).

Размеры — это числовое значение линейной величины (диаметра, длины и т.д.), они делятся на номинальные, действительные и предельные. В машино и приборостроении все размеры в технической документации задают и указывают в миллиметрах.

Номинальный размер (D) — размер, относительно которого определяют предельные размеры и отсчитывают отклонения. Номинальные размеры являются основными размерами деталей или их соединений. Сопрягаемые поверхности имеют общий номинальный размер.

Действительный размер (Dr, dr) — размер, установленный измерением с допустимой погрешностью. Погрешностью измерения называется отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерения, а следовательно, и выбор измерительных средств необходимо согласовывать с точностью, которая требуется для данного размера.

Предельные размеры — два предельно допустимых размера, между которыми должен находиться или которым может быть равен действи¬тельный размер. Больший из двух предельных размеров называют наибольшим предельным размером (Dmax, dmax), а меньший — наименьшим предельным размером (Dmin, dmin) Предельные размеры позво¬ляют оценивать точность обработки деталей.

Отклонение — это алгебраическая разность между действительным и соответствующим номинальными размерами. Отклонения отверстий обозначают буквой E, валов — e.

Действительное отклонение (Er, er) равно алгебраической разности действительного и номинального размеров: Er = Dr — D; er = dr — d.

Предельное отклонение равно алгебраической разности предельного и номинального размеров. Различают верхнее, нижнее и среднее отклонения. Верхнее (ES, es) равно алгебраической разности наибольшего предельного и номинального размеров: ES = Dmax — D; es = dmax — D.

Нижнее отклонение (EI, ei) равно алгебраической разности наименьшего предельного и номинального размеров: EI = Dmin — D; ei = Dmin — D.
Среднее отклонение (Em, em) равно полусумме верхнего и ниж¬него отклонений: Em = 0,5 (ES + EI), em = 0,5 (es + ei).
Пример. Определить предельные и средние отклонения для штифтов, у которых D = 20 мм, dmax = 20,01 мм и dmin = 19,989 мм.

Для графического построения полей допусков и посадок проводят горизонтальную линию 00, называемую нулевой. Нулевая — это линия, положение которой соответствует номинальному размеру и от которой откладываются предельные отклонения размеров. По-ложительные отклонения — вверх от нулевой линии, отрицательные — вниз.

Поле допуска — поле, ограниченное верхним и нижним отклонения¬ми. Оно опре-деляется величиной допуска и его положением относитель¬но номинального размера. При графическом изображении поля допусков показывают зоны, которые ограничены двумя ли-ниями, проведенными на расстояниях, соответствующих верхнему и нижнему отклоне¬нию.
На схемах указывают номинальный D и предельные (Dmax, Dmin, dmax, dmin) размеры, предельные отклонения (ES, EI, es, ei) поля допусков и другие параметры.

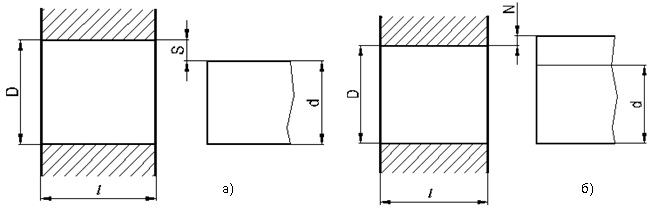
Понятия о посадках и допуске посадки. Если у соединяемых между собой деталей размер отверстия больше размера вала, то в соединении будет зазор (S). Если же размер ва-ла больше размера отверстия, то в соединении будет натяг (N). Зазором называется по-ложительная разность между размерами отверстия и вала S = D — d (рис. 42, а). а натягом — положительная разность между размером вала и отверстия N = d — D (рис. 42, б).

В машинах и приборах требуются посадки с различными зазорами и натягами. В тех случаях, когда одна деталь должна перемещаться относительно другой без качки, следует иметь очень малый зазор: для того чтобы одна деталь могла свободно вращаться в другой (например, вал в отверстии), зазор должен быть больше. Если соединенные вал и втулка представляют собой как бы одно целое, они соединены с натягом и не могут перемещаться относительно друг друга.
Посадки подразделяют на три вида: подвижные, обеспечивающие зазор в соединении: неподвижные (прессовые), обеспечивающие натяг в соединении; переходные, ко-торые наз¬ваны так потому, что до сборки вала и втулки нельзя сказать, что будет в соединении — зазор или натяг, так как заданные отклонения на вал и отверстие перекрывают друг друга.

В зависимости от использованного допуска у той и другой детали при переходной посадке может оказаться, что размер вала больше размера отверстия или размер отверстия больше размера вала.

Для оценки точности соединений (посадок) пользуются понятием допуска посадки, под которым понимается разность между наибольшим и наименьшим зазорами (в посадках с зазором) или наибольшим и наименьшим натягами (в посадках с натягом). В переходных посадках допуск посадки равен разности между наибольшим и наименьшим натягами или сумме наибольшего натяга и наибольшего зазора. Допуск посадки равен также сумме допусков отверстия и вала.

Источник