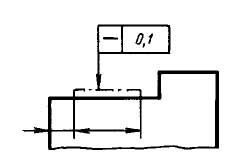
что такое допуск симметричности

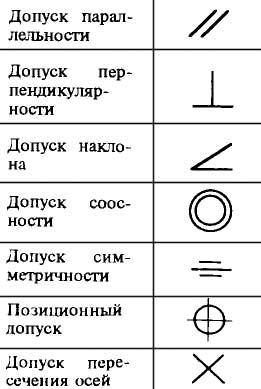
Допуск симметричности

Зачастую в технике встречаются симметричные детали, их применение обуславливается простотой в изготовлении и установки при сборочных операциях. Как и у всех изделий, симметричные детали в процессе производства, получаются отличными от геометрии номинального размера. Для указания отклонения таких деталей используют допуск симметричности.

На чертеже допуск симметричности выглядит в виде трёх горизонтально и параллельно расположенных линий, одна из которых несколько длиннее двух остальных, расположенных сверху и снизу на одинаковом расстоянии отступа.

Фигура, расположенная на плоскости считается симметричной, если при мысленном изгибании относительно осевой линии, её части совпадают. Симметрия также существует в пространстве, которую её ещё называют зеркальной, так как обе части фигуры расположенные относительно общей секущей плоскости, по сути, расположены как в зеркальном отражении.

При выполнении чертежей деталей, помимо параллельности и величины шероховатости, довольно часто ставится допуск симметричности. При соблюдении перечисленных параметров геометрии шпоночного паза, сборочная операция проводится без каких бы, то ни было затруднений и нарушений технологической дисциплины.

Слово симметрия произошло от греческого «symmetria», что означает соразмерность. Симметрия в эстетическом понимании является признаком полноты и совершенства выражаемом в пропорциональности, гармонии, однородности и упорядоченности структуры.

Симметрия встречается не только в геометрических особенностях строения тел в природе, но и в ряде направлений человеческой деятельности, которые зачастую заимствуются. Симметрия встречается в искусстве, науке и технике. Во всех направлениях симметрия имеет одинаковые определяющие характеристики при разных постановках условий реализации.

В архитектурных орнаментах различных древних сооружений зачастую встречаются геометрические фантазии мастеров воплощенных в виде разнообразных барельефов и других частей классических построек. Одними из жёстких условий, которыми предписывалось придерживаться при реализации творческого замысла в древности, являлось соблюдение принципов симметрии.

В различных произведениях искусства, на ряду, с симметричными элементами образующими строение эстетического объекта, встречаются ассиметричные включения, которые зачастую встраиваются в общую симметричную структуру.

Асимметрия, это состояние природных и искусственных объектов, визуально оцениваемых как противоположных симметрии. Асимметрия не является полным отрицанием симметрии, так как асимметричные фигуры могут характеризоваться наличием бесконечного числа осей первого порядка, которые также представляют собой элементы симметрии.

Геометрическая характеристика простых форм, представляемая как отображение простых геометрических фигур на плоскости, а так же в пространстве, реализуется в виде: круга, квадрата, треугольника, цилиндра, и т.д. Сложные формы образуются в результате объединения не менее двух, каких либо простых форм.

Каждая из геометрических фигур определяется такими параметрами как масштабность, пропорциональность, органичность и целостность внешних форм, объемно-пространственное строение, симметричность и асимметричность.

Источник

Допуски формы и расположения

Любая технологическая операция может быть выполнена с определенной точностью, а значит размеры полученной в результате обработки детали не будут идеальными, они могут колебаться в некотором диапазоне. Для того, чтобы выполнить условия собираемости и обеспечить надежную работу детали в заданных условиях необходимо задать допустимый интервал, в который должен попасть итоговый размер. Этот интервал может регламентировать не только линейные или диаметральные размеры, но и форму или взаимное расположение поверхностей.

Допуски формы и расположения назначаются конструктором исходя из условий сборки и особенностей работы детали в механизме.

Виды допусков формы

Отклонения и допуски формы

Различают следующие допуски на отклонения формы:

Допустимые отклонения обозначаются специальными символами.

Виды допусков расположения

Различают допуски месторасположения и допуски ориентации.

Отклонения и допуски расположения

Различают следующие виды допусков расположения:

Эти допуски обозначаются символами.

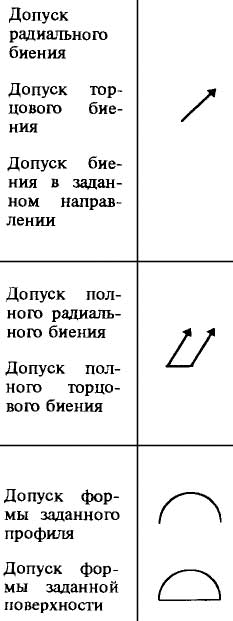
Суммарные допуски

Существует несколько видов суммарных допусков формы и расположения.

Эти допуски обозначаются символами.

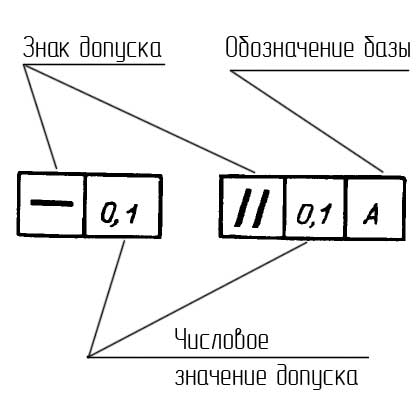
Обозначение допусков формы и расположения на чертежах

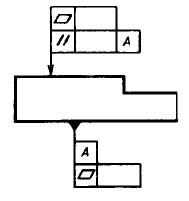
В случае отсутствия базы допуска рамка состоит только из двух частей. Примеры рамок допусков формы и расположения показаны на рисунке.

На рисунке слева показана рамка с допуском формы (допустимое отклонение от прямолинейности), справа с допуском расположения (допустимое отклонение от параллельности).

Рамку выполняют тонкими линиями. Высота текста в рамке должна равняться размеру шрифта размерных чисел. От рамки допуска до поверхности или до выноски проводится линия, оканчивающаяся стрелкой.

Перед числовым значение допуска могут указываться знаки:

Если допуск должен применяться не ко всей поверхности, а только к некоторому участку, то он обозначается штрих пунктирной линией.

Для одного элемента может быть указано несколько допусков, этом случае рамки изображаются одна над другой.

Дополнительная информация может быть указана над рамкой или под ней.

Информация о допусках формы и расположения может быть указана в технических требованиях.

Зависимые допуски

Зависимые допуски расположения обозначают следующим символом .

Этот символ может быть размещен после числового значения допуска, если зависимый допуск связан с действительными размерами рассматриваемого элемента. Также символ может быть размещен после буквенного обозначение (если оно отсутствует то в третьем поле рамки) в том случае, если зависимый допуск связан с действительными размерами базового элемента.

Назначение допусков формы и расположения

Чем точнее изготовлена деталь, тем более точные инструменты потребуются для ее изготовления и контроля размеров. Это автоматически увеличит ее стоимость. Получается, что цена изготовления детали во многом зависит от требуемой точности при ее изготовлении. Это означает, что конструктор должен указать лишь те допуски, которые действительно необходимы для сборки и надежной работы механизма. Допустимые интервалы также должны быть назначены исходя из условий собираемости и работоспособности.

В ГОСТе 24643-81 указаны рекомендации по назначению допусков формы и расположения поверхностей

Числовые значения допусков формы

В зависимости от класса точности устанавливаются стандартные значения допусков формы.

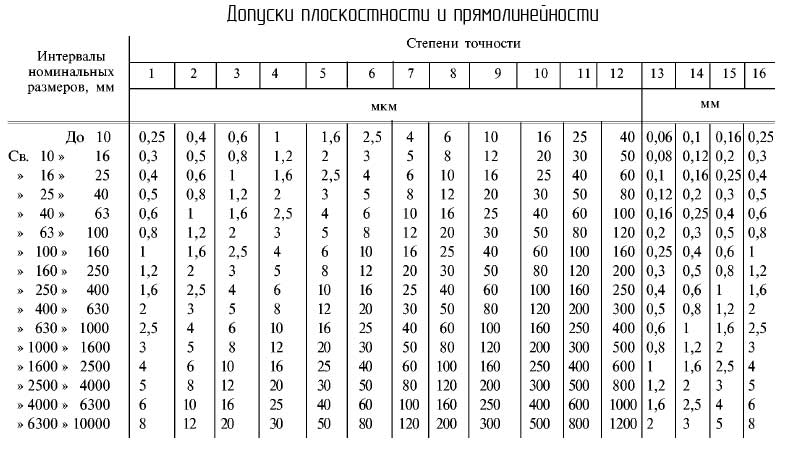
Допуски плоскостности и прямолинейности

Номинальным размеров в данном случае считается номинальная длина нормированного участка.

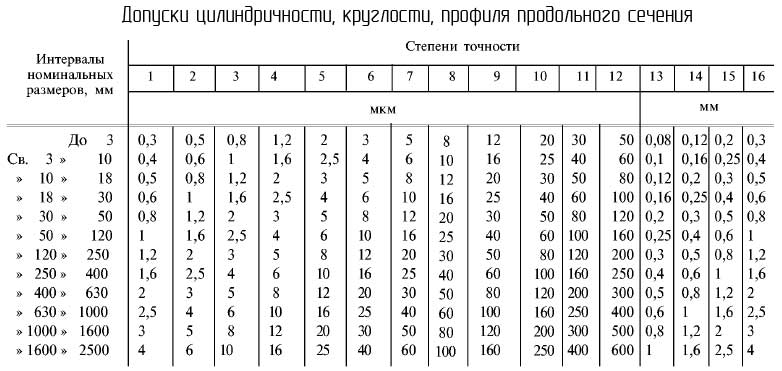
Допуски круглости, цилиндричности, профиля продольного сечения

Данные допуски назначаются в тех случаях, когда они должны быть меньше, чем допуск размера.

Номинальным размером считается номинальный диаметр поверхности.

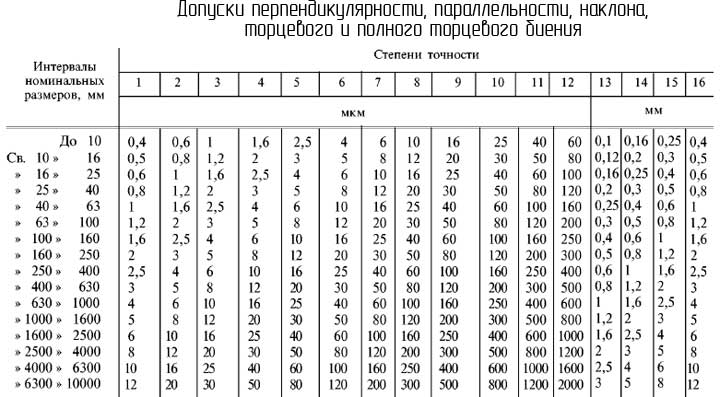
Допуски перпендикулярности, параллельности, наклона, торцевого биения

Номинальным размером при назначении допусков на параллельность, перпендикулярность, наклон понимается номинальная длина нормируемого участка или номинальная длина всей контролируемой поверхности.

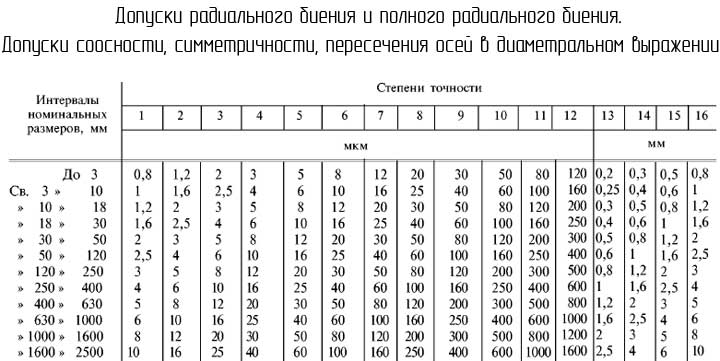
Допуски радиального биения, симметричности, соосности пересечения осей в диаметральном выражении

При назначении допусков радиального биения номинальным размером считается номинальный диаметр рассматриваемой поверхности.

В случае назначения допусков симметричности, пересечения осе соосности номинальным размером считается номинальный диаметр поверхности или номинальный размер между поверхностями, которые образуют рассматриваемый элемент.

Источник

Что такое допуск симметричности

Допуск пересечения осей

Суммарные допуски формы и расположения

Допуск радиального биения

Допуск торцового биения

Допуск биения в заданном направлении

Допуск полного радиального биения

Допуск полного торцового биения

Допуск формы заданного профиля

Допуск формы заданной поверхности

Формы и размеры знаков приведены в приложении 1.

Примеры указания на чертежах допусков формы и расположения поверхностей приведены в приложении 2.

Примечание. Суммарные допуски формы и расположения поверхностей, для которых не установлены отдельные графические знаки, обозначают знаками составных допусков в следующей последовательности: знак допуска расположения, знак допуска формы.

— знак суммарного допуска параллельности и плоскостности;

— знак суммарного допуска перпендикулярности и плоскостности;

— знак суммарного допуска наклона и плоскостности.

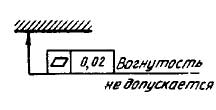
1.2. Допуск формы и расположения поверхностей допускается указывать текстом в технических требованиях, как правило, в том случае, если отсутствует знак вида допуска.

1.3. При указании допуска формы и расположения поверхностей в технических требованиях текст должен содержать:

указание поверхности или другого элемента, для которого задается допуск (для этого используют буквенное обозначение или конструктивное наименование, определяющее поверхность);

числовое значение допуска в миллиметрах;

указание баз, относительно которых задается допуск (для допусков расположения и суммарных допусков формы и расположения);

указание о зависимых допусках формы или расположения (в соответствующих случаях).

1.4. При необходимости нормирования допусков формы и расположения, не указанных на чертеже числовыми значениями и не ограничиваемых другими указанными в чертеже допусками формы и расположения, в технических требованиях чертежа должна быть приведена общая запись о неуказанных допусках формы и расположения со ссылкой на ГОСТ 25069-81* или другие документы, устанавливающие неуказанные допуски формы и расположения.

* С 1 января 2004 г. введен в действие ГОСТ 30893.2-2002 (здесь и далее).

(Введен дополнительно, Изм. N 1).

2. НАНЕСЕНИЕ ОБОЗНАЧЕНИЙ ДОПУСКОВ

2.1. При условном обозначении данные о допусках формы и расположения поверхностей указывают в прямоугольной рамке, разделенной на две и более части (черт.1, 2), в которых помещают:

2.2. Рамки следует выполнять сплошными тонкими линиями. Высота цифр, букв и знаков, вписываемых в рамки, должна быть равна размеру шрифта размерных чисел.

Графическое изображение рамки приведено в приложении 1.

2.3. Рамку располагают горизонтально. В необходимых случаях допускается вертикальное расположение рамки.

Не допускается пересекать рамку какими-либо линиями.

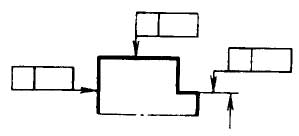
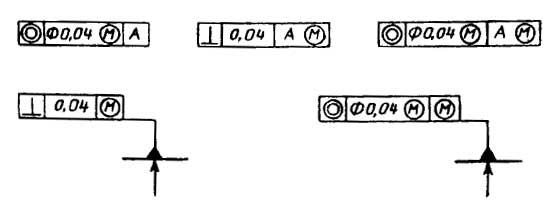
2.4. Рамку соединяют с элементом, к которому относится допуск, сплошной тонкой линией, заканчивающейся стрелкой (черт.3).

Соединительная линия может быть прямой или ломаной, но направление отрезка соединительной линии, заканчивающегося стрелкой, должно соответствовать направлению измерения отклонения. Соединительную линию отводят от рамки, как показано на черт.4.

В необходимых случаях допускается:

проводить соединительную линию от второй (последней) части рамки (черт.5а);

заканчивать соединительную линию стрелкой и со стороны материала детали (черт.5б).

2.5. Если допуск относится к поверхности или ее профилю, то рамку соединяют с контурной линией поверхности или ее продолжением, при этом соединительная линия не должна быть продолжением размерной линии (черт.6, 7).

2.6. Если допуск относится к оси или плоскости симметрии, то соединительная линия должна быть продолжением размерной линии (черт.8а, б). При недостатке места стрелку размерной линии допускается совмещать со стрелкой соединительной линии (черт.8в).

Если размер элемента уже указан один раз, то на других размерных линиях данного элемента, используемых для условного обозначения допуска формы и расположения, его не указывают. Размерную линию без размера следует рассматривать как составную часть условного обозначения допуска формы или расположения (черт.9).

2.7. Если допуск относится к боковым сторонам резьбы, то рамку соединяют с изображением в соответствии с черт.10а.

Если допуск относится к оси резьбы, то рамку соединяют с изображением в соответствии с черт.10б.

Источник

Что такое допуск симметричности

Основные нормы взаимозаменяемости

ДОПУСКИ ФОРМЫ И РАСПОЛОЖЕНИЯ ПОВЕРХНОСТЕЙ

Основные термины и определения

Basic norms of interchangeability. Tolerances of form and position.
Basic terms and definitions

Дата введения 1981-07-01

1. РАЗРАБОТАН И ВНЕСЕН Министерством станкостроительной и инструментальной промышленности СССР

2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 18.03.81 N 1423

3. Стандарт полностью соответствует СТ СЭВ 301-88

4. Стандарт соответствует в части терминологии международным стандартам ИСО 1101-83, ИСО 5459-81

5. ВЗАМЕН ГОСТ 10356-63 (в части разд.I и II)

6. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ

Обозначение НТД, на который дана ссылка

7. ИЗДАНИЕ с Изменением N 1, утвержденным в октябре 1989 г. (ИУС 1-90)

Настоящий стандарт устанавливает термины и определения, относящиеся к основным видам отклонений и допусков формы и расположения поверхностей деталей машин и приборов.

Стандарт содержит приложения 1-6, в которых приведены дополнительные пояснения отдельных терминов, отмеченных *, указатели терминов на английском, немецком и французском языках, дополнительные параметры отклонений формы, а также алфавитные указатели терминов на русском языке и обозначений.

1. ОБЩИЕ ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ

Обобщенный термин, под которым в зависимости от соответствующих условий может пониматься поверхность, линия, точка

Линия пересечения поверхности с плоскостью или заданной поверхностью.

Примечание. Если в технической документации не указано иное, то направление секущей плоскости определяется по нормали к поверхности

1.3. Номинальная форма

Идеальная форма элемента, которая задана чертежом или другими техническими документами

1.4. Номинальная поверхность

Идеальная поверхность, размеры и форма которой соответствуют заданным номинальным размерам и номинальной форме

1.5. Номинальный профиль

1.6. Реальная поверхность

1.7. Реальный профиль

Примечание к пп.1.6 и 1.7. Реальная поверхность и реальный профиль в определениях отклонений формы и расположения по настоящему стандарту понимаются без учета шероховатости поверхности

1.8. Нормируемый участок*

Участок поверхности или линии, к которому относятся допуск формы, допуск расположения, суммарный допуск формы и расположения или соответствующие отклонения.

Примечание. Если нормируемый участок не задан, то допуск формы, допуск

расположения, суммарный допуск формы и расположения или соответствующие отклонения должны относиться ко всей рассматриваемой поверхности или длине рассматриваемого элемента

1.9. Базовый элемент для оценки отклонений формы*

Элемент номинальной формы, служащий основой для оценки отклонений формы реальной поверхности или реального профиля.

Примечание. Базовый элемент для оценки отклонений формы используется также для исключения влияния отклонений формы при определении отклонений расположения

1.10. Прилегающая поверхность

Поверхность, имеющая форму номинальной поверхности, соприкасающаяся с реальной поверхностью и расположенная вне материала детали так, чтобы отклонение от нее наиболее удаленной точки реальной поверхности в пределах нормируемого участка имело минимальное значение.

Примечание. Условие минимального значения отклонения не распространяется на прилегающий цилиндр (см. п.1.12)

1.11. Прилегающая плоскость

Плоскость, соприкасающаяся с реальной поверхностью и расположенная вне материала детали так, чтобы отклонение от нее наиболее удаленной точки реальной поверхности в пределах нормируемого участка имело минимальное значение

1.12. Прилегающий цилиндр

Цилиндр минимального диаметра, описанный вокруг реальной наружной поверхности, или цилиндр максимального диаметра, вписанный в реальную внутреннюю поверхность.

Примечание. В тех случаях, когда расположение прилегающего цилиндра относительно реальной поверхности неоднозначно, он принимается по условию минимального значения отклонения

1.13. Прилегающий профиль

Профиль, имеющий форму номинального профиля, соприкасающийся с реальным профилем и расположенный вне материала детали так, чтобы отклонение от него наиболее удаленной точки реального профиля в пределах нормируемого участка имело минимальное значение.

Примечание. Условие минимального значения отклонения не распространяется на прилегающую окружность (см. п.1.15)

1.14. Прилегающая прямая

Прямая, соприкасающаяся с реальным профилем и расположенная вне материала детали так, чтобы отклонение от нее наиболее удаленной точки реального профиля в пределах нормируемого участка имело минимальное значение

1.15. Прилегающая окружность

Окружность минимального диаметра, описанная вокруг реального профиля наружной поверхности вращения, или окружность максимального диаметра, вписанная в реальный профиль внутренней поверхности вращения.

Примечание. В тех случаях, когда расположение прилегающей окружности относительно реального профиля неоднозначно, оно принимается по условию минимального значения отклонения

1.16. Прилегающий профиль продольного сечения

Две параллельные прямые, соприкасающиеся с реальным профилем осевого (продольного) сечения цилиндрической поверхности и расположенные вне материала детали так, чтобы наибольшее отклонение точек реального профиля от соответствующей стороны прилегающего профиля продольного сечения в пределах нормируемого участка имело минимальное значение

Геометрическое место центров сечений поверхности вращения, перпендикулярных оси прилегающей поверхности.

Примечание. За центр сечения принимается центр прилегающей окружности. Ось прилегающей поверхности вращения

1.18. Геометричес- кая ось реальной поверхности вращения*

1.19. Отклонение формы*

Отклонение формы реального элемента от номинальной формы, оцениваемое наибольшим расстоянием от точек реального элемента по нормали к прилегающему элементу.

1. Шероховатость поверхности не включается в отклонение формы. В обоснованных случаях допускается нормировать отклонение формы, включая шероховатость поверхности.

2. Волнистость включается в отклонение формы. В обоснованных случаях допускается нормировать отдельно волнистость поверхности или часть отклонения формы без учета волнистости.

3. Особым случаем оценки отклонения формы является отклонение от прямолинейности оси (см. пп.2.1.4. и 2.1.5).

Наибольшее допускаемое значение отклонения формы

1.21. Поле допуска формы

Элемент детали (или выполняющее ту же функцию сочетание элементов), по отношению к которому задается допуск расположения или суммарный допуск формы и расположения рассматриваемого элемента, а также определяется соответствующее отклонение

Совокупность двух или трех баз, образующих систему координат, по отношению к которой задается допуск расположения или суммарный допуск формы и расположения рассматриваемого элемента, а также определяется соответствующее отклонение

1.24. Участок базирования*

Точка, линия или ограниченная площадь на базовой поверхности детали, в которых должен быть обеспечен контакт детали с базирующими элементами обрабатывающего или контрольного оборудования с целью установления баз, необходимых для удовлетворения функциональных требований

Прямая, относительно которой наибольшее отклонение осей нескольких рассматриваемых поверхностей вращения в пределах длины этих поверхностей имеет минимальное значение

1.26. Общая плоскость симметрии

Плоскость, относительно которой наибольшее отклонение плоскостей симметрии нескольких рассматриваемых элементов в пределах длины этих элементов имеет минимальное значение

1.27. Номинальное расположение*

Расположение рассматриваемого элемента (поверхности или профиля), определяемое номинальными линейными и угловыми размерами между ним и базами или между рассматриваемыми элементами, если базы не заданы

1.28. Реальное расположение

Расположение рассматриваемого элемента (поверхности или профиля), определяемое действительными линейными и угловыми размерами между ним и базами или между рассматриваемыми элементами, если базы не заданы

1.29. Отклонение расположения*

Отклонение реального расположения рассматриваемого элемента от его номинального расположения.

1. Количественно отклонения расположения оцениваются в соответствии с определениями, приведенными в пп.3.1-3.7.

2. При оценке отклонений расположения отклонения формы рассматриваемых элементов и баз должны исключаться из рассмотрения. При этом реальные поверхности (профили) заменяются прилегающими, а за оси плоскости симметрии и центры реальных поверхностей или профилей принимаются оси, плоскости симметрии и центры прилегающих элементов

1.30. Допуск расположения*

Предел, ограничивающий допускаемое значение отклонения расположения

1.31. Поле допуска расположения

1.32. Выступающее поле допуска расположения

Поле допуска или часть его, ограничивающее отклонение расположения рассматриваемого элемента за пределами протяженности этого элемента (нормируемый участок выступает за пределы длины элемента)

1.33. Зависимый допуск расположения

Зависимый допуск формы*

Допуск расположения или формы, указываемый на чертеже или в других технических документах в виде значения, которое допускается превышать на величину, зависящую от отклонения действительного размера рассматриваемого элемента и/или базы от предела максимума материала (наибольшего предельного размера вала или наименьшего предельного размера отверстия)

1.34. Независимый допуск расположения

Независимый допуск формы

Допуск расположения или формы, числовое значение которого постоянно для всей совокупности деталей и не зависит от действительного размера рассматриваемого элемента и/или базы

1.35. Суммарное отклонение формы и расположения*

Отклонение, являющееся результатом совместного проявления отклонения формы и отклонения расположения рассматриваемой поверхности или рассматриваемого профиля относительно баз.

Примечание. Количественно суммарные отклонения формы и расположения оцениваются в соответствии с определениями, приведенными в пп.4.1-4.7, по точкам реального рассматриваемого элемента относительно прилегающих базовых элементов или их осей.

1.36. Суммарный допуск формы и расположения

Предел, ограничивающий допускаемое значение суммарного отклонения формы и расположения

1.37. Поле суммарного допуска формы и расположения

2. ОТКЛОНЕНИЯ И ДОПУСКИ ФОРМЫ

2.1. Отклонение от прямолинейности и допуск прямолинейности

2.1.1. Отклонение от прямолинейности в плоскости*

Наибольшее расстояние от точек реального профиля до прилегающей прямой в пределах нормируемого участка

2.1.2. Допуск прямолинейности

Наибольшее допускаемое значение отклонения от прямолинейности

2.1.3. Поле допуска прямолинейности в плоскости

Область на плоскости, ограниченная двумя параллельными прямыми, отстоящими друг от друга на расстоянии, равном допуску прямолинейности

2.1.4. Отклонение от прямолинейности оси (или линии) в пространстве

Наименьшее значение диаметра цилиндра, внутри которого располагается реальная ось поверхности вращения (линия) в пределах нормируемого участка

2.1.5. Отклонение от прямолинейности оси (или линии) в заданном направлении

Наименьшее расстояние между двумя параллельными плоскостями, перпендикулярными к плоскости заданного направления, в пространстве между которыми располагается реальная ось поверхности вращения (линия) в пределах нормируемого участка

2.1.6. Поле допуска прямолинейности оси (или линии) в пространстве

1) Область в пространстве, ограниченная цилиндром, диаметр которого равен допуску прямолинейности

3) Область в пространстве, ограниченная двумя параллельными плоскостями, отстоящими друг от друга на расстоянии, равном допуску прямолинейности оси (или линии) и перпендикулярными плоскости заданного направления

2.2. Отклонение от плоскостности и допуск плоскостности

2.2.1. Отклонение от плоскостности*

Наибольшее расстояние от точек реальной поверхности до прилегающей плоскости в пределах нормируемого участка

2.2.2. Допуск плоскостности

Наибольшее допускаемое значение отклонения от плоскостности

2.2.3. Поле допуска плоскостности

Область в пространстве, ограниченная двумя параллельными плоскостями, отстоящими друг от друга на расстоянии, равном допуску плоскостности

2.3. Отклонение от круглости и допуск круглости

2.3.1. Отклонение от круглости*

Наибольшее расстояние от точек реального профиля до прилегающей окружности

2.3.2. Допуск круглости

Наибольшее допускаемое значение отклонения от круглости

2.3.3. Поле допуска круглости

Область на поверхности, перпендикулярной оси поверхности вращения или проходящей через центр сферы, ограниченная двумя концентричными окружностями, отстоящими друг от друга на расстоянии, равном допуску круглости

2.4. Отклонение от цилиндричности и допуск цилиндричности

2.4.1. Отклонение от цилиндричности

Наибольшее расстояние от точек реальной поверхности до прилегающего цилиндра в пределах нормируемого участка

2.4.2. Допуск цилиндричности

Наибольшее допускаемое значение отклонения от цилиндричности

2.4.3. Поле допуска цилиндричности

Область в пространстве, ограниченная двумя соосными цилиндрами, отстоящими друг от друга на расстоянии, равном допуску цилиндричности

2.5. Отклонение и допуск профиля продольного сечения цилиндрической поверхности

2.5.1. Отклонение профиля продольного сечения*

Наибольшее расстояние от точек реальной поверхности, лежащих в плоскости, проходящей через ее ось, до соответствующей стороны прилегающего профиля в пределах нормируемого участка

2.5.2. Допуск профиля продольного сечения

Наибольшее допускаемое значение отклонения профиля продольного сечения

2.5.3. Поле допуска профиля продольного сечения

Области на плоскости, проходящей через ось цилиндрической поверхности, ограниченные двумя парами параллельных прямых, имеющих общую ось симметрии и отстоящих друг от друга на расстоянии, равном допуску профиля продольного сечения

3. ОТКЛОНЕНИЯ И ДОПУСКИ РАСПОЛОЖЕНИЯ

3.1. Отклонение от параллельности и допуск параллельности

3.1.1. Отклонение от параллельности плоскостей

Разность наибольшего и наименьшего расстояний между плоскостями в пределах нормируемого участка

3.1.2. Допуск параллельности

Наибольшее допускаемое значение отклонения от параллельности

3.1.3. Поле допуска параллельности плоскостей

3.1.4. Отклонение от параллельности оси (или прямой) и плоскости

Разность наибольшего и наименьшего расстояний между осью (прямой) и плоскостью на длине нормируемого участка

3.1.5. Поле допуска параллельности оси (или прямой) в плоскости

3.1.6. Отклонение от параллельности прямых в плоскости

Разность наибольшего и наименьшего расстояний между прямыми на длине нормируемого участка

3.1.7. Поле допуска параллельности прямых в плоскости

3.1.8. Отклонение от параллельности осей (или прямых) в пространстве*

Геометрическая сумма отклонений от параллельности проекций осей (прямых) в двух взаимно перпендикулярных плоскостях; одна из этих плоскостей является общей плоскостью осей

3.1.8.1. Отклонение от параллельности осей (или прямых) в общей плоскости

Отклонение от параллельности проекций осей (прямых) на их общую плоскость

3.1.8.2. Перекос осей (или прямых)

Отклонение от параллельности проекций осей (прямых) на плоскость, перпендикулярную к общей плоскости осей и проходящую через одну из осей (базовую)

3.1.8.3. Допуск параллельности осей (прямых) в общей плоскости

3.1.8.4. Допуск перекоса осей (прямых)

3.1.9. Поле допуска параллельности осей (или прямых) в пространстве

1) Область в пространстве, ограниченная прямоугольным параллелепипедом, стороны сечения которого равны соответственно допуску параллельности осей (прямых) в общей плоскости и допуску перекоса осей (прямых) , а боковые грани параллельны базовой оси и соответственно параллельны и перпендикулярны к общей плоскости осей

3.2. Отклонение от перпендикулярности и допуск перпендикулярности

3.2.1. Отклонение от перпендикулярности плоскостей

Отклонение угла между плоскостями от прямого угла (90°), выраженное в линейных единицах на длине нормируемого участка

3.2.2. Допуск перпендикулярности*

Наибольшее допускаемое значение отклонения от перпендикулярности

3.2.3. Поле допуска перпендикулярности плоскостей

3.2.4. Отклонение от перпендикулярности плоскости или оси (или прямой) относительно оси (прямой)

Отклонение угла между плоскостью или осью (прямой) и базовой осью от прямого угла (90°), выраженное в линейных единицах на длине нормируемого участка

3.2.5. Поле допуска перпендикулярности плоскости или оси (или прямой) относительно оси (прямой)

3.2.6. Отклонение от перпендикулярности оси (или прямой) относительно плоскости в заданном направлении

Отклонение угла между проекцией оси поверхности вращения (прямой) на плоскость заданного направления (перпендикулярную к базовой плоскости) и базовой плоскостью от прямого угла (90°), выраженное в линейных единицах на длине нормируемого участка

3.2.7. Поле допуска перпендикулярности оси (или прямой) относительно плоскости в заданном направлении

Область на плоскости заданного направления, ограниченная двумя параллельными прямыми, отстоящими друг от друга на расстоянии, равном допуску перпендикулярности и перпендикулярности к базовой плоскости

3.2.8. Отклонение от перпендикулярности оси (или прямой) относительно плоскости*

Отклонение угла между осью поверхности вращения (прямой) и базовой плоскостью от прямого угла (90°), выраженное в линейных единицах на длине нормируемого участка

3.2.9. Поле допуска перпендикулярности оси (или прямой) относительно плоскости

2) Область в пространстве, ограниченная прямоугольным параллелепипедом, стороны сечения которого равны допускам перпендикулярности оси (прямой) в двух заданных взаимно перпендикулярных направлениях и , боковые грани перпендикулярны к базовой плоскости и плоскостям заданных направлений

3.3. Отклонение и допуск наклона*

3.3.1. Отклонение наклона плоскости относительно плоскости или оси (или прямой)

Отклонение угла между плоскостью и базовой плоскостью или базовой осью (прямой) от номинального угла, выраженное в линейных единицах на длине нормируемого участка

Наибольшее допускаемое значение отклонения наклона

3.3.3. Поле допуска наклона плоскости относительно плоскости или оси (или прямой)

3.3.4. Отклонение наклона оси (или прямой) относительно оси (прямой) или плоскости*

Отклонение угла между осью поверхности вращения (прямой) и базовой осью или базовой плоскостью от номинального угла, выраженное в линейных единицах на длине нормируемого участка

3.3.5. Поле допуска наклона оси (или прямой) относительно оси (прямой) или плоскости

3.4. Отклонение от соосности и допуск соосности*

3.4.1. Отклонение от соосности

Наибольшее расстояние между осью рассматриваемой поверхности вращения и базой (осью базовой поверхности или общей осью двух или нескольких поверхностей) на длине нормируемого участка

3.4.2. (Исключен, Изм. N 1).

3.4.4. Поле допуска соосности

3.5. Отклонение от симметричности и допуск симметричности

3.5.1. Отклонение от симметричности

Наибольшее расстояние между плоскостью симметрии (осью) рассматриваемого элемента (или элементов) и базой (плоскостью симметрии базового элемента или общей плоскостью симметрии двух или нескольких элементов) в пределах нормируемого участка

3.5.2. (Исключен, Изм. N 1)

3.5.3. Допуск симметричности*

3.5.4. Поле допуска симметричности

3.6. Позиционное отклонение и позиционный допуск

3.6.1. Позиционное отклонение

Наибольшее расстояние между реальным расположением элемента (его центра, оси или плоскости симметрии) и его номинальным расположением в пределах нормируемого участка

3.6.2. Позиционный допуск*

3.6.3. Поле позиционного допуска оси (или прямой) в плоскости

Область на плоскости, ограниченная двумя параллельными прямыми, отстоящими друг от друга на расстоянии, равном позиционному допуску в диаметральном выражении или удвоенному позиционному допуску в радиусном выражении , и симметричная относительно номинального расположения рассматриваемой оси (прямой)

3.6.4. Поле позиционного допуска оси (или прямой) в пространстве

2) Область в пространстве, ограниченная прямоугольным параллелепипедом, стороны сечения которого равны позиционным допускам и в диаметральном выражении или удвоенным позиционным допускам в радиусном выражении и в двух взаимно перпендикулярных направлениях, а боковые грани соответственно перпендикулярны плоскостям заданных направлений

3.6.5. Поле позиционного допуска плоскости симметрии или оси в заданном направлении

Область в пространстве, ограниченная двумя параллельными плоскостями, отстоящими друг от друга на расстоянии, равном позиционному допуску в диаметральном выражении или удвоенному позиционному допуску в радиусном выражении , и симметричными относительно номинального расположения рассматриваемой плоскости симметрии (см. чертеж) или оси; для позиционных допусков оси в заданном направлении плоскости, ограничивающие поле допуска, перпендикулярны заданному направлению

3.7. Отклонение от пересечения и допуск пересечения осей

3.7.1. Отклонение от пересечения осей

Наименьшее расстояние
между осями, номинально пересекающимися

3.7.2. Допуск пересечения осей*

3.7.3. Поле допуска пересечения осей

Область в пространстве, ограниченная двумя параллельными плоскостями, отстоящими друг от друга на расстоянии, равном допуску пересечения в диаметральном выражении или удвоенному допуску пересечения в радиусном выражении , и расположенными симметрично относительно базовой оси

4. СУММАРНЫЕ ОТКЛОНЕНИЯ И ДОПУСКИ ФОРМЫ И РАСПОЛОЖЕНИЯ

4.1. Радиальное биение и допуск радиального биения

4.1.1. Радиальное биение*

Разность наибольшего и наименьшего расстояний от точек реального профиля поверхности вращения до базовой оси в сечении плоскостью, перпендикулярной базовой оси

4.1.2. Допуск радиального биения

Наибольшее допускаемое значение радиального биения

4.1.3. Поле допуска радиального биения

Область на плоскости, перпендикулярной к базовой оси, ограниченная двумя концентричными окружностями с центром, лежащим на базовой оси, и отстоящими друг от друга на расстоянии, равном допуску радиального биения

4.2. Торцовое биение и допуск торцового биения

Разность наибольшего и наименьшего расстояний от точек реального профиля торцовой поверхности до плоскости, перпендикулярной к базовой оси.

Примечание. Торцовое биение определяется в сечении торцовой поверхности цилиндром заданного диаметра, соосным с базовой осью, а если диаметр не задан, то в сечении любого (в том числе и наибольшего) диаметра торцовой поверхности

4.2.2. Допуск торцового биения

Наибольшее допускаемое значение торцового биения

4.2.3. Поле допуска торцового биения

4.3. Биение и допуск биения в заданном направлении

4.3.1. Биение в заданном направлении*

Разность наибольшего и наименьшего расстояний от точек реального профиля поверхности вращения в сечении рассматриваемой поверхности конусом, ось которого совпадает с базовой осью, а образующая имеет заданное направление, до вершины этого конуса

4.3.2. Допуск биения в заданном направлении

Наибольшее допускаемое значение биения в заданном направлении

4.3.3. Поле допуска биения в заданном направлении

4.4. Полное радиальное биение и допуск полного радиального биения*

4.4.1. Полное радиальное биение*

Разность наибольшего и наименьшего расстояний от всех точек реальной поверхности в пределах нормируемого участка до базовой оси

4.4.2. Допуск полного радиального биения

Наибольшее допускаемое значение полного радиального биения

4.4.3. Поле допуска полного радиального биения

Область в пространстве, ограниченная двумя цилиндрами, ось которых совпадает с базовой осью, а боковые поверхности отстоят друг от друга на расстоянии, равном допуску полного радиального биения

4.5. Полное торцовое биение и допуск полного торцового биения*

4.5.1. Полное торцовое биение*

Разность наибольшего и наименьшего расстояний от точек всей торцовой поверхности до плоскости, перпендикулярной к базовой оси

4.5.2. Допуск полного торцового биения

Наибольшее допускаемое значение полного торцового биения

4.5.3. Поле допуска полного торцового биения

Область в пространстве, ограниченная двумя параллельными плоскостями, отстоящими друг от друга на расстоянии, равном допуску полного торцового биения и перпендикулярными к базовой оси

4.6. Отклонение и допуск формы заданного профиля*

4.6.1. Отклонение формы заданного профиля*

Наибольшее отклонение точек реального профиля от номинального профиля, определяемое по нормали к номинальному профилю в пределах нормируемого участка

4.6.2. Допуск формы заданного профиля*

4.6.3. Поле допуска формы заданного профиля

4.7. Отклонение и допуск формы заданной поверхности*

4.7.1. Отклонение формы заданной поверхности*

Наибольшее отклонение точек реальной поверхности от номинальной поверхности, определяемое по нормали к номинальной поверхности в пределах нормируемого участка

4.7.2. Допуск формы заданной поверхности*

4.7.3. Поле допуска формы заданной поверхности

Область в пространстве, ограниченная двумя поверхностями, эквидистантными номинальной поверхности, и отстоящими друг от друга на расстоянии равном допуску формы заданной поверхности в диаметральном выражении или удвоенному допуску формы заданной поверхности в радиусном выражении .

Источник