что такое доказательство в математике
Математическое доказательство
На протяжении всей истории математики представление о способах и допустимых методах доказательства существенно менялось, в основном, в сторону большей формализации и бо́льших ограничений. Ключевой вехой в вопросе формализации доказательства стало создание математической логики в XIX веке и формализация её средствами основных техник доказательства. В XX веке построена теория доказательств — теория, изучающая доказательство как математический объект. С появлением во второй половине XX века компьютеров особое значение получило применение методов математического доказательства для проверки и синтеза программ, и даже было установлено структурное соответствие между компьютерными программами и математическими доказательствами (соответствие Карри — Ховарда), на основе которого созданы средства автоматического доказательства.
Основные приёмы, используемые при построении доказательств: прямое доказательство, математическая индукция и её обобщения, доказательство от противного, контрапозиция, построение, перебор, установление биекции, двойной счёт; в приложениях в качестве математических доказательств привлекаются также методы, не дающие формального доказательства, но обеспечивающие практическую применимость результата — вероятностные, статистические, приближённые. В зависимости от раздела математики, используемого формализма или математической школы не все методы могут приниматься безоговорочно, в частности, конструктивное доказательство предполагает серьёзные ограничения.
Математическое доказательство
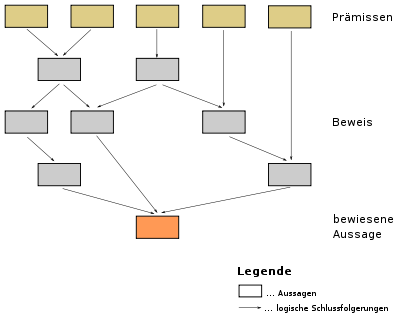
В математике доказа́тельством называется цепочка логических умозаключений, показывающая, что при каком-то наборе аксиом и правил вывода верно некоторое утверждение. В зависимости от контекста, может иметься в виду доказательство в рамках некоторой формальной системы (построенная по специальным правилам последовательность утверждений, записанная на формальном языке) или текст на естественном языке, по которому при желании можно восстановить формальное доказательство. Доказанные утверждения в математике называют теоремами (в математических текстах обычно подразумевается, что доказательство кем-либо найдено; исключения из этого обычая в основном составляют работы по логике, в которых исследуется само понятие доказательства); если ни утверждение, ни его отрицание ещё не доказаны, то такое утверждение называют гипотезой. Иногда в процессе доказательства теоремы выделяются доказательства менее сложных утверждений, называемых леммами.
Содержание
Формальными доказательствами занимается специальная ветвь математики — теория доказательств. Сами формальные доказательства математики почти никогда не используют, поскольку для человеческого восприятия они очень сложны и часто занимают очень много места. Обычно доказательство имеет вид текста, в котором автор, опираясь на аксиомы и доказанные ранее теоремы, с помощью логических средств показывает истинность некоторого утверждения. В отличие от других наук, в математике недопустимы эмпирические доказательства: все утверждения доказываются исключительно логическими способами. В математике важную роль играют математическая интуиция и аналогии между разными объектами и теоремами; тем не менее, все эти средства используются учёными только при поиске доказательств, сами доказательства не могут основываться на таких средствах. Доказательства, написанные на естественных языках, могут быть не очень подробными в расчёте на то, что подготовленный читатель сам сможет восстановить детали. Строгость доказательства гарантируется тем, что его можно представить в виде записи на формальном языке (это и происходит при компьютерной проверке доказательств).
Ошибочным доказательством называется текст, содержащий логические ошибки, то есть такой, по которому нельзя восстановить формальное доказательство. В истории математики были случаи, когда выдающиеся учёные публиковали неверные «доказательства», однако обычно их коллеги или они сами довольно быстро находили ошибки (одна из наиболее часто неправильно доказывавшихся теорем — Великая теорема Ферма. До сих пор встречаются люди, не знающие о том, что она доказана, и предлагающие новые неверные «доказательства» [1] [2] ). Ошибочным может быть только признание доказательством «доказательства» на естественном или формальном языке; формальное доказательство ошибочным не может быть по определению.
В математике существуют нерешённые проблемы, решение которых учёным очень хотелось бы найти. Некоторые из них можно найти в статье «Гипотеза». За доказательства особенно интересных и важных утверждений математические общества назначают премии. [источник не указан 1311 дней]
В информатике математические доказательства используются для верификации и анализа правильности алгоритмов и программ. см. логика в информатике> в рамках технологий доказательного программирования.
Формальное доказательство
Когда говорят о формальном доказательстве, прежде всего описывают формальную модель — множество аксиом, записанных с помощью формального языка, и правил вывода. Формальным выводом называется конечное упорядоченное множество строк, написанных на формальном языке, таких, что каждая из них либо является аксиомой, либо получена из предыдущих строк применением одного из правил вывода. Формальным доказательством утверждения называется формальный вывод, последней строкой которого является данное утверждение. Утверждение, имеющее формальное доказательство, называется теоремой, а множество всех теорем в данной формальной модели (рассматриваемое вместе с алфавитом формального языка, множествами аксиом и правил вывода) называется формальной теорией.
Теория называется полной, если для любого утверждения доказуемо оно или его отрицание, и непротиворечивой, если в ней не существует утверждений, которые можно доказать вместе с их отрицаниями (или, эквивалентно, если в ней существует хотя бы одно недоказуемое утверждение). Большинство «достаточно богатых» математических теорий, как показывает первая теорема Гёделя о неполноте, являются неполными либо противоречивыми. Самым распространённым набором аксиом в наше время является аксиоматика Цермело — Френкеля с аксиомой выбора (хотя некоторые математики выступают против использования последней). Теория на основе этой системы аксиом не полна (например, континуум-гипотеза не может быть ни доказана, ни опровергнута в ней — в предположении, что эта теория непротиворечива). Несмотря на повсеместное использование этой теории в математике, её непротиворечивость не может быть доказана методами её самой. Тем не менее, подавляющее большинство математиков верит в её непротиворечивость, считая, что в противном случае противоречия уже давно были бы обнаружены.
Исторический очерк
Что и требовалось доказать
Традиционно окончание доказательства обозначалось сокращением «Q.E.D.», от латинского выражения лат. Quod Erat Demonstrandum («Что и требовалось доказать»).
Что такое аксиома, теорема и доказательство теоремы
Понятие аксиомы
Аксиома — это правило, которое считают верным и которое не нужно доказывать. В переводе с греческого «аксиома» значит принятое положение — то есть взяли и договорились, что это истина, с которой не поспоришь.
Аксиоматический метод — это подход к получению знаний, при котором сначала разрабатывают аксиомы, а потом с их помощью формулируют новые теории.
Синоним аксиомы — постулат. Антоним — гипотеза.
Основные аксиомы евклидовой геометрии
Учить наизусть эти аксиомы не обязательно. Главное — помнить о них и держать под рукой, чтобы при доказательстве теоремы сослаться на одну из них.
А теперь давайте рассмотрим несколько аксиом из геометрии за 7 и 8 класс.
Самая известная аксиома Евклида — аксиома о параллельных прямых. Звучит она так:
Это значит, что если дана прямая и любая точка, которая не лежит на этой прямой, то через неё можно провести только одну единственную прямую, которая будет параллельна этой первой данной прямой.
У этой аксиомы два следствия:
Аксиома Архимеда заключается в том, что, если отложить достаточное число раз меньший из двух отрезков, то можно покрыть больший из них. Звучит так:
Если на прямой есть меньший отрезок А и больший отрезок B, то, можно сложить А достаточное количество раз, чтобы покрыть B.
На картинке можно увидеть, как это выглядит:
Из этого следует, что не существует бесконечно малых и бесконечно больших величин. В качестве математической формулы аксиому можно записать так: А + А + … + А = А * n > В, где n — это натуральное число.
Понятие теоремы
Что такое аксиома мы уже поняли, теперь узнаем определение теоремы.
Теорема — логическое следствие аксиом. Это утверждение, которое основано на аксиомах и общепринятых утверждениях, которые были доказаны ранее, и доказывается на их основе.
Состав теоремы: условие и заключение или следствие.
Среди теорем выделяют такие, которые сами по себе не используются в решениях задач. Но их используют для доказательства других теорем.
Лемма — это вспомогательная теорема, с помощью которой доказываются другие теоремы. Пример леммы: если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая тоже пересекает эту плоскость.
Следствие — утверждение, которое выводится из аксиомы или теоремы. Следствие, как и теорему, необходимо доказывать.
Примеры следствий из аксиомы о параллельности прямых:
Доказательство теоремы — это процесс обоснования истинности утверждения.
Каждая доказанная теорема служит основанием доказательства для следующей теоремы. Именно поэтому так важно изучать геометрию последовательно, переходя от аксиом к теоремам.
Способы доказательства геометрических теорем
Часть аналитического способа — доказательство от противного, когда для доказательства данного предложения убеждают в невозможности предположения противоположного.
Приемы для доказательства в геометрии:
Обратная теорема — это такой перевертыш: в ней условие исходной теоремы дано заключением, а заключение — условием.
Прямая и обратная теорема взаимно-обратные. Например:
В первой теореме данное условие — это равенство сторон треугольника, а заключение — равенство противолежащих углов. А во второй всё наоборот.
Противоположная теорема — это утверждение, в котором из отрицания условия вытекает отрицание заключения.
Вот, как выглядит взаимное отношение теорем на примере:
В геометрическом изложении достаточно доказать только две теоремы, тогда остальные справедливы без доказательства.
Записывайся на онлайн обучение по математике для учеников с 1 по 11 классы!
Доказательство через синтез
Рассмотрим пример синтетического способа доказательства.
Теорема: сумма углов треугольника равна двум прямым.
Дан треугольник: ABC. Нужно доказать, что A + B + C = 2d.
Доказательство:
Проведем прямую DE, так чтобы она была параллельна AC.
Сумма углов, лежащих по одну сторону прямой, равна двум прямым, следовательно, α + B + γ = 2d.
Так как α = A, γ = C, то заменим в предыдущем равенстве углы α и γ равными им углами: A + B + C = 2d. Что и требовалось доказать.
Здесь исходным предложением в цепи доказательств выбрана теорема о сумме углов, которые лежат по одну сторону прямой. Есть связь с теоремами о равенстве углов накрест-лежащих при пересечении двух параллельных третьею косвенною. Доказываемая теорема есть необходимое следствие всех предложенных теорем и является в цепи доказательств последним заключением.
Доказательство через анализ
Рассмотрим пример аналитического способа доказательства.
Теорема: диагонали параллелограмма пересекаются пополам.
Дан параллелограмм: ABCD.
Доказательство:
Если диагонали пересекаются пополам, то треугольники AOB и DOC равны.
Равенство же треугольников AOB и DOC вытекает из того, что AB = CD, как противоположные стороны параллелограмма и ∠α = ∠γ, ∠β = ∠δ, как накрест-лежащие углы.
Таким образом мы видим, что последовательно данное предложение заменяется другим и такое замещение совершается до тех пор, пока не дойдем до уже доказанного предложения.
Теоремы без доказательств
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
Доказательств может быть несколько. Одно из них звучит так: если построить квадраты на сторонах прямоугольного треугольника, то площадь большего из них равна сумме площадей меньших квадратов. На картинке понятно, как это работает:
Теорема косинусов: квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. В виде формулы это выглядит так:
где a, b и c — стороны плоского треугольника,
α — угол напротив стороны а.
Следствия из теоремы косинусов:
Понятия свойств и признаков
У нас есть список аксиом и мы уже знаем, что такое теорема и как ее доказывать. Есть два типа утверждений среди теорем, которые часто встречаются при изучении новых фигур: свойства и признаки.
Свойства и признаки — понятия из обычной жизни, которые мы часто используем.
Свойство — такое утверждение, которое должно выполняться для данного типа объектов. У ноутбука есть клавиатура — это свойство есть у каждого ноутбука. А у электронной книги такого свойства нет.
Примеры геометрических свойств мы уже знаем: у квадрата все стороны равны. Это верно для любого квадрата, поэтому это — свойство.
Такое свойство можно встретить у другого четырехугольника. И клавиатура может быть на других устройствах, помимо ноутбука. Из этого следует, что свойства не обязательно должны быть уникальными.
Признак — это то, по чему мы однозначно распознаем объект.
Звезды в темном небе — признак того, что сейчас ночь. Если человек ходит с открытым зонтом — это признак того, что сейчас идет дождь. При этом ночью не обязательно должны быть видны звезды, иногда может быть облачно. Значит это не свойство ночи.
А теперь вернемся к геометрии и рассмотрим четырехугольник ABCD, в котором AB = BD = 10 см.
Является ли равенство диагоналей признаком прямоугольника? У такого четырехугольника, где AB = BD, диагонали равны, но он не является прямоугольником. Это свойство, но не его признак.
Но если в четырехугольнике противоположные стороны параллельны AB || DC и AD || BC и диагонали равны AB = BD, то это уже верный признак прямоугольника. Смотрите рисунок:
Иногда свойство и признак могут быть эквивалентны. Лужи — это верный признак дождя. У других природных явлений не бывает луж. Но если приходит дождь, то лужи на асфальте точно будут. Значит, лужи — это не только признак, но и свойство дождя.
Такие утверждения называют необходимым и достаточным признаком.
Доказательство (математика)
оглавление
Конструктивные и неконструктивные доказательства
Доказательства существования
В случае неконструктивного доказательства существование решения выводится из свойств. Иногда даже косвенное предположение об отсутствии решения приводит к противоречию, из которого следует, что решение существует. Такие доказательства не говорят, как найти решение.
Простой пример должен прояснить это.
Теория множеств
Вся математика может быть построена на ZFC и проверена в рамках ZFC. Работающий математик обычно не излагает основ теории множеств, упоминается только использование выбранной аксиомы, обычно в форме леммы Цорна. Всегда даются дополнительные теоретические предположения о множестве, например, при использовании гипотезы континуума или ее отрицания.
Официальные доказательства
Формальные доказательства сводят шаги доказательства к серии определенных операций над строками. Такие доказательства обычно могут быть созданы только с помощью машины (см., Например, Coq (программное обеспечение) ), и они едва различимы для людей, даже перевод доказываемых предложений на чисто формальный язык приводит к очень длинным, громоздким и непонятным. струны. С тех пор был формализован ряд хорошо известных предложений, и их формальное доказательство было проверено машиной. Однако, как правило, математиков удовлетворяет уверенность в том, что их цепочки аргументов в принципе могут быть перенесены в формальные доказательства, не выполняя их на самом деле; они используют методы доказательства, представленные ниже.
Методы доказательства
Прямые доказательства
Для прямого доказательства ( прямого заключения ) берется утверждение, правильность которого уже доказана (посылка), и выводится доказываемое утверждение (вывод) из него посредством логических выводов. В качестве простого примера рассмотрим следующее:
Из возможности представить это следует, что это странно. п 2 <\ Displaystyle п ^ <2>> 
Косвенные доказательства
А теперь пример reductio ad absurdum:
Еще один классический пример:
Полная индукция
Полное различие падежей
В случае доказывания путем исчерпания каждый из возможных случаев рассматривается индивидуально. Следовательно, количество возможных случаев должно быть конечным.
Диагональный метод
Диагональные методы были разработаны Георгом Кантором для доказательства двух специальных утверждений. С тех пор они зарекомендовали себя как общие методы доказательства.
Первый диагональный метод Кантора является прямым доказательством счетности множества. Показано, что каждому элементу исследуемого множества можно присвоить натуральное число.
Второй диагонали метод Кантора является косвенным доказательством для несчетности набора. Таким образом, предполагается обратное, а именно, что множество счетно. Тогда из этого предположения выводится противоречие, так что его нужно отброс ить.
Принцип ящика / принцип голубятни
Трансфинитная индукция
Математика
This wiki’s URL has been migrated to the primary fandom.com domain.Read more here
Математическое доказательство
Ошибочным доказательством называется текст, содержащий логические ошибки, то есть такой, по которому нельзя восстановить формальное доказательство. В истории математики были случаи, когда выдающиеся учёные публиковали неверные «доказательства», однако обычно их коллеги или они сами довольно быстро находили ошибки. (Одна из наиболее часто неправильно доказывавшихся теорем — Великая теорема Ферма. До сих пор встречаются люди, не знающие о том, что она доказана, и предлагающие новые неверные «доказательства».) Ошибочным может быть только признание «доказательства» на естественном или формальном языке доказательством; формальное доказательство ошибочным не может быть по определению.
В математике существуют нерешённые проблемы, решение которых учёным очень хотелось бы найти. Некоторые из них можно найти в статье « Гипотеза ». За доказательства особенно интересных и важных утверждений математические общества назначают премии.
Формальное доказательство
Теория называется полной, если для любого утверждения доказуемо либо оно, либо его отрицание, и непротиворечивой, если в ней не существует утверждений, которые можно доказать вместе с их отрицаниями. Большинство математических теорий, как показывает первая теорема Гёделя о неполноте, являются неполными, то есть в них существуют утверждения, об истинности которых ничего сказать нельзя. Самым распространённым набором аксиом в наше время является аксиоматика Цермело — Френкеля с аксиомой выбора (хотя некоторые математики выступают против использования последней). Теория на основе этой системы аксиом не полна (например, континуум-гипотеза не может быть ни доказана, ни опровергнута в ней). Несмотря на повсеместное использование этой теории в математике, её непротиворечивость не может быть доказана методами её самой. Тем не менее, подавляющее большинство математиков верит в её непротиворечивость, считая, что в противном случае противоречия уже давно были бы обнаружены.
См. также
ar:برهان رياضي ca:Demostració matemàtica cs:Matematický důkaz da:Bevis (matematik) fa:برهان he:הוכחה hu:Matematikai bizonyítás is:Stærðfræðileg sönnun ka:დამტკიცება mk:Математички доказ nds:Bewies (Mathematik) nl:Wiskundig bewijs no:Matematisk bevis pl:Dowód (matematyka) sl:Matematični dokaz th:การพิสูจน์ vi:Chứng minh định lý zh-classical:證明 zh-min-nan:Chèng-bêng