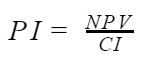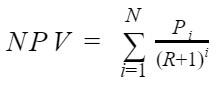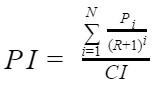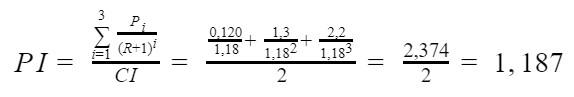что такое доходность индекса
Индекс доходности инвестиций. Показатель индекса доходности инвестиций
Оценка проектов
Принцип определения эффективности заключается в сравнении анализируемого показателя с базовой величиной. В вопросе вложений таковыми являются банковский депозит и дисконтная ставка. Выгодными считаются инвестиции, доход по которым превышает прибыль от депозита.
Для анализа проектов используются показатели:
Рассмотрим каждый из них детальнее.
Чистая текущая стоимость (NPV)
Данный показатель рассчитывается как разность между инвестицией и текущей стоимостью выплат. NPV исключает фактор времени. Если значение текущей стоимости > 0 – проект прибыльный; равно 0 – увеличение объемов не будет способствовать росту прибыли; t ] – IC, где:
Пример расчета NPV
Для удобства и наглядности все нужные цифры мы поместили в таблицу.
| Поступления | Вложения | Ставка дисконтирования |
| 0 | 279 | 0,91 |
| 0 | 186 | 0,83 |
| 186 | 0 | 0,75 |
| 279 | 0 | 0,68 |
| 372 | 0 | 0,62 |
Рассчитаем текущую стоимость проекта
1. Дисконтированный доход:
PV = 186 х 0,75 + 279 х 0,69 + 372 х 0.62 = 561,3 тыс. руб.
2. Дисконтированная сумма вложений:
PV = 279 х 0,91 + 186 х 0,83 = 407,3 тыс. руб.
3. Чистая стоимость инвестиций:
NPV = 561.3 – 407,3 = 154 тыс. руб.
Ключевым моментом при расчете NPV является выбор учетной ставки. В этом процессе нужно учитывать размер безрисковых (банковских) ставок, норму издержек, неопределенность, риск долгосрочных вложений и др.
Дисконтирование потоков денежных средств отображает проект, приносящий больше доходов. Но «лучшей» инвестицией может быть и безрисковая.
Норма рентабельности (IRR)
Данный коэффициент характеризует максимальную стоимость инвестиций (расходов), которые могут быть понесены в рамках данного проекта. Если финансирование осуществляется за счет ссуды банка, то значение IRR показывает верхнюю границу ставки обслуживания. В случае ее превышения проект будет убыточным. Экономический смысл: предприятие может принимать решения, рентабельность которых превышает текущую цену средств – СС:
PI 1 = 1 + 244,4 / 500 = 1 + 0,49 = 1,49.
PI 2 = 1 + 340,4 / 780 = 1 + 0,44 = 1,44.
Скорость изменения цены
ROC показывает, как изменилась цена на данный момент по сравнению с n-м периодом в прошлом. Он может быть представлен в пунктах или процентах.
Индекс доходности дисконтированных инвестиций
В случае единовременного вложения капитала в проект рассчитывается дисконтированный индекс:
Если процесс инвестирования разбит на несколько этапов, то показатель будет рассчитываться по иной формуле:
Как рассчитать индекс рентабельности инвестиций (PI)
Финансирование коммерческих проектов всегда сопряжено с рисками. Опасения вызывает достоверность прогнозирования по извлечению чистой прибыли. Даже самая тщательная оценка бизнес-плана основана на предположениях. Трудно предвидеть объемы продаж, а от них зависит соотношение получаемых доходов и сделанных вложений.
Несмотря на сложности, развитие бизнеса невозможно без взвешенного подхода к делу. Следовательно, предварительный анализ нужен, и одним из его критериев служит индекс рентабельности инвестиций. Статья рассказывает о том, как его рассчитать.
Что такое индекс рентабельности инвестиций (PI)
Понятия рентабельности, прибыльности и доходности в экономике означают степень эффективности работы вложенных средств. Эти показатели близки по смыслу физическому коэффициенту полезного действия.
В общем виде оценка доходности затрат производится по их результативности. Коэффициент рентабельности характеризует отношение суммы входящих денежных потоков к величине капитала, израсходованного на их получение. Он легко определяется «задним числом», методом деления одного показателя на другой.
Задача усложняется, если планируется финансирование инвестиционного проекта с трудно-прогнозируемым экономическим эффектом.
Индекс прибыльности (PI – аббревиатура английского термина Profitability Index) определяется как результат отношения сумм дисконтированного дохода и вложенного капитала. Иными словами, индекс показывает, сколько копеек приносит каждый рубль, потраченный на реализацию проекта. Особого пояснения требует слово «дисконтированный». В контексте, термин означает перерасчет прибыли с учетом фактора времени.
В течение срока реализации проекта деньги успевают обесцениться за счет инфляции. Средства, размещенные на банковском депозите, обеспечивают пассивную прибыль по годовой ставке с минимальным риском и без всяких хлопот. По этой причине о доходности инвестиций финансист судит по возможным последствиям размещения тех же средств, но в другие объекты. При этом, он оценивает сопутствующие факторы:
Немалую роль играет опыт проведения аналогичных операций.
В конечном счете формируется решение, основанное на относительной доходности, то есть на соотношении предполагаемой прибыли с некими базовыми значениями.
Чем выше индекс рентабельности проекта, тем привлекательней бизнес, нуждающийся в финансировании. Обычной ситуацией считается наличие альтернативных предложений. При выборе лучшего варианта для вложений требуется сравнение нескольких инвестиционных проектов.
Необходим единый подход, позволяющий не допустить ошибку. Важна бывает и интуиция, присущая наиболее прозорливым бизнесменом, но без объективной оценки не обойтись. Критерием принятия оптимального решения выступает коэффициент доходности инвестиций, рассчитанный для каждого объекта вложения.
Как рассчитать индекс доходности
Метод определения рентабельности инвестиции (PI) проекта вкратце описан выше. Посчитать этот показатель можно по формуле:
Как видно из математического выражения, индекс представляет безразмерный коэффициент: числитель и знаменатель — оба выражены в денежных единицах, которые взаимно сокращаются.
В некоторых случаях для удобства и наглядности PI измеряется в процентах. Для этого значение следует умножить на 100%.
Чтобы дисконтировать (привести к актуальным условиям) доход, следует воспользоваться еще одной формулой:
Значение R устанавливается инвестором и является его внутренней нормой. В некоторых случаях оно равно ставке рефинансирования Центрального банка РФ, но чаще превышает ее. Дело в том, что у крупного предпринимателя есть альтернативные варианты вложений, обеспечивающие ему определенную отдачу. Отвлекая средства на менее рентабельные направления, бизнесмен несет потери.
После простой подстановки, формула PI приобретает окончательный вид:
Теперь можно рассмотреть пример расчета.
После подстановки значений получается результат:
Из полученной итоговой суммы дисконтированного дохода (в числителе формулы) можно сделать вывод о том, что она больше вложенного капитала, а значение PI указывает, во сколько раз.
Очевидно, что за трехлетний период времени инвестору вернутся деньги, превышающие сумму вложений на 18,7%.
Анализ PI-индекса
Индекс прибыльности – индикатор, экономический смысл которого выражает заинтересованность инвестора в проекте. Чем больше можно заработать, тем выше ПИ (PI). NPV, то есть дисконтированный суммарный денежный поток наглядно показывает, сколько средств получит финансист за один оборот капитала. Таким образом, анализ дает двойные итоги: абсолютный и относительный.
Рассчитанный индекс доходности инвестиций прост в оценке. Если сравнивать его с единицей, возможны три варианта:
Индекс доходности инвестиций (коэффициент эффективности)
Инвестиционные проекты оцениваются большим количеством показателей, но наиболее часто используются статические показатели: срок окупаемости инвестиций (PP), индекс доходности инвестиций (PI), коэффициент эффективности инвестиций (ARR); динамические: приведенная чистая стоимость проекта (NPV), индекс доходности дисконтированных инвестиций (DPI) и внутренняя норма доходности инвестиционного проекта(IRR).
Коэффициент эффективности вложений

Для оценки коэффициента за полный цикл жизни инвестиционного проекта используют следующую расчетную формулу:
Если ликвидационная стоимость проекта равна 0, то в знаменателе будет половина начальной стоимости инвестиционного проекта.
В данном примере основные фонды проекта полностью амортизированы, т. е. ликвидационная стоимость равна 0.
Данный показатель используют при оценке целесообразности вложений в проект, сравнивая его с процентной ставкой банковских кредитов или со стоимостью капитала инвестиционного объекта. Более полезен он для сравнительной оценки нескольких конкурентных инвестиционных проектов.
Индекс доходности инвестиций

Если сумма доходов меньше размера инвестиций, то проект не окупает себя и не может рассматриваться к применению. Если PI>1 проект может быть принят.
Более точным показателем является индекс доходности дисконтированных инвестиций (DPI), который определяется как:
It – размер инвестиций в t-ом году.
Данный показатель рассчитывается главным образом при разнесенных по времени инвестициях в один и тот же инвестиционный проект.
Срок жизни проекта 5 лет.
Дисконтированный индекс доходности инвестиционного проекта DPI >1, поэтому проект может быть принят к исполнению. Если бы расчет проводился при инвестиционных вложениях произведенных единовременно в начале проекта, то:
Наиболее ценным для анализа эффективности инвестиционного проекта среди названных является внутренняя норма доходности инвестиций IRR.

Сравнивая этот показатель с доходностью капитала инвестируемого объекта можно оценивать его целесообразность.
Расчет показателя осуществляется путем последовательных итераций до момента, когда чистая приведенная стоимость NPV меняет знак «минус» на знак «плюс». Для этого расчета используются таблицы дисконтируемых множителей, с помощью которых находят ту норму доходности, при которой NPV=0.
Более наглядным расчет выглядит в графическом изображении:
На графике представлены изменения NPV двух инвестиционных проектов: А и Б. Их NPV отражаются по оси ординат, а норма доходности отражается % по оси абсцисс. Пересечение NPV проектов с осью абсцисс дает показания их внутренней нормы доходности: для проекта А она равна 14,7%, а для проекта Б 11,8%. При доходности капитала инвестируемого объекта в 12% проект Б не может быть принят к исполнению, да и проект А не обладает необходимым запасом устойчивости по показателю доходности. Также следует оценивать проекты при кредитной ставке привлекаемых ресурсов в 11% годовых.
Сразу надо отметить, что если денежные потоки на протяжении исследуемого периода времени меняют знак с плюса на минус или наоборот, то расчет IRR становится невозможным, а если его рассчитывают, то он не отражает реальной нормы доходности проекта.
Для нашего вышеприведенного примера, когда PI показывает негативные результаты, рассчитаем IRR с применением таблиц дисконтируемых множителей. Выберем норму доходности близкую к расчетной r=11% и r=12%.
Что характеризует индекс по доходности и как рассчитать его формулу
Инвестор, прежде чем вкладывать средства в какое-либо предприятие, стремится проанализировать, какая прибыль может быть получена в результате. К числу параметров, посредством которых оцениваются перспективы развития бизнес-проекта, относится PI — индекс доходности. Термин имеет несколько названий — Present value index или прибыльности, DPI или рентабельности.
Понятие рентабельности или индекса доходности
Рентабельность проекта обозначает его прибыльность. С помощью этого показателя оценивают потенциальную доходность любого бизнеса. На практике понятие рентабельности широко применяют для оценки экономического состояния предприятия, конкурентоспособности выпускаемой продукции или оказываемых услуг. Для этого отдельный вид продукции сравнивают с таковым у конкурирующих компаний или с другим видом товара, выпускаемого предприятием.
Этот индекс, как показатель, является универсальным. С его помощью можно сравнивать эффективность и прибыльность проектов различного масштаба. Если выразить индекс как понятие в числах, оно отобразит цифру чистой прибыли, делённую на количество затраченных ресурсов. Поэтому возникло понятие — рентабельности вложенного капитала или, простыми словами, доходности.
Индекс рентабельности инвестпроекта: методика и формулы
Profitability Index для оценки инвестиций задействую, оценивая относительную доходность различных вложений средств. Рассчитать его величину можно с помощью матформулы:
NPV это чистая стоимость входящих инвестпотоков в реальном времени в рублях. I — величина вкладов в инвестпроект в рублях. Для инвестиций Индекс по доходности используют при оценке относительной отдачи предназначенных для идеи финансов. Если вливания капитала в крупный бизнес-проект разнесены на длительный период, в формулу вводится величина дисконтирования по средней норме отдачи за год.
Значение показателей индекса по доходности
Рассчитывать индекс доходности нужно, чтобы определить возможную эффективность от инвестиции в конкретный бизнес-проект, и успешно ли составлен бизнес-план. Чем выше цифра индекса рентабельности для вложений, тем больший доход способна принести идея в перспективе. Результаты анализа полученных данных характеризуются следующим образом:
Роль индекса по доходности в оценке бизнес-плана
Любой бизнес-план требует проведения серии расчётов в финансовой части. Здесь учитывается несколько главных показателей. На их основании судят о пригодности проекта к воплощению в жизнь. К числу показателей относятся:
Чтобы бизнес-план был принят и одобрен, необходимо, чтобы чистая дисконтированная прибыль была выше 0, а время окупаемости проекта было минимальным. Оценить ставку дисконта можно разными способами. Если планируется вложить кредитные деньги, то минимальной величиной дисконтирования должна быть процентная ставка по кредиту. Здесь полученная прибыль позволит покрыть расходы. Иначе инвестору гораздо выгоднее направить финансы на счёт в банковское учреждение и не рисковать ими в инвестпроектах.
Если же инвестиции проводятся из собственных финансов, ставка доходности вложений должна равняться или быть большей, чем уровень уже имеющейся доходности бизнесмена. Кроме того, цифра ставки дисконтирования нужна меньшей величины налога на прибыль с имеющегося капитала.
Исходя из этих факторов, проводить оценку рентабельности предприятия всегда нужно по нескольким параметрам — индексу доходности, дисконтной ставке и текущей стоимости всех инвестиций. Определение индекса доходности требуется проводить не только перед принятием бизнес-проекта в момент выбора, но и в ходе реализации и после завершения.
Большое значение имеет и величина, обратная индексу. Она называется сроком окупаемости для инвестиций (РР — Pay-Back-Period). Этот показатель позволяет определить, как скоро инвестор получит доход от вложения своего капитала. В России доходы от инвестиционных проектов можно ожидать спустя 3 года. Это связано с особенностями экономических процессов в стране. Для кредитных средств предельным сроком окупаемости считается 5 лет. В странах с развитой экономикой период составляет 7 лет.
Расчёт доходности в таблице Excel
Один из наиболее простых способов расчёта индекса — оценка с помощью Excel. Ее использует большинство инвесторов, так как она отличается простотой, высокой точностью и скоростью операций. С помощью таких таблиц можно подсчитать дисконтированные расходы и прибыль.
Разработано 2 варианта расчётов доходности. Первый из них отличается простым алгоритмом для индекса:
Для доходности существует второй вариант — более сложный. В нем используется встроенная формула, которая помогает рассчитывать параметры, необходимые для определения дисконтированной прибыли.
Достоинства и проблемы показателя доходности
Индекс доходности даёт вкладчику большое количество преимуществ. Можно сравнивать несколько инвестпроектов различных по объёму вложений. Показатель позволяет также применять ставку дисконтирования к инвестидеям, когда трудно прогнозировать и формализовать часть данных. Формулы для обработки довольно просты и не требуют установки дополнительного программного обеспечения. Достаточно внести все исходные в таблицу Excel.
Наряду с этим, индекс имеет некоторые недостатки, которые проявляются во время его использования:
Не всегда получается спрогнозировать уровень влияния различных факторов на финпотоки.
Для некоторых идей норму дисконта бывает сложно вычислить.
Это касается и расчёта планируемых финпотоков.
Стабильность финансовых поступлений обусловлена несколькими внешними факторами. Среди них ведущую роль играют ключевая ставка Центробанка, затраты на приобретение материалов и сырья, а также объёмы реализации готовой продукции. Немаловажную роль играет также действующая финансовая политика компании, и какая экономическая обстановка на тот или иной момент наблюдается в государстве. Все эти факторы оказывают непосредственное влияние на ставку дисконта, следовательно, доходность.
Спрогнозировать их бывает не всегда легко. Чем больше предполагаемый срок жизни проекта, тем выше неопределённость при расчётах. В качестве примера можно привести наложение санкций на некоторые российские предприятия, что негативно отразилось на их экономическом состоянии.
Таким образом, при внешней простоте расчётов по формуле индекса доходности могут возникать неожиданные затруднения, снижающие точность показателя.
По каким формулам и в какой программе вы рассчитываете показатель доходности?
Как считать индикаторы инвестиционной привлекательности активов
На примере портфеля Уоррена Баффетта
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
((1 + 20%) × (1 − 10%) × (1 + 30%)) 1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному : акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%) 1/4 = 15,8%.
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%) 1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность) (365 / Количество дней владения активом) − 1
(1 + 74%) (365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива) (1 / Количество периодов) − 1
((270 × 20 + 2 × 20) / 200 × 20) (1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как победить выгорание
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Правило трех сигм гласит, что практически все значения нормально распределенной случайной величины лежат в диапазоне трех стандартных отклонений от среднего арифметического значения случайной величины. Случайной величиной у нас выступает годовая доходность по акции
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.