что такое додекаэдр в геометрии

Фигура в природе

Правильный многогранник считается шаблоном, привлекает безупречным совершенством формы и абсолютной симметричностью сторон. Природной моделью геометрической фигуры является кристалл пирита (FeS — колчедан сернистый).

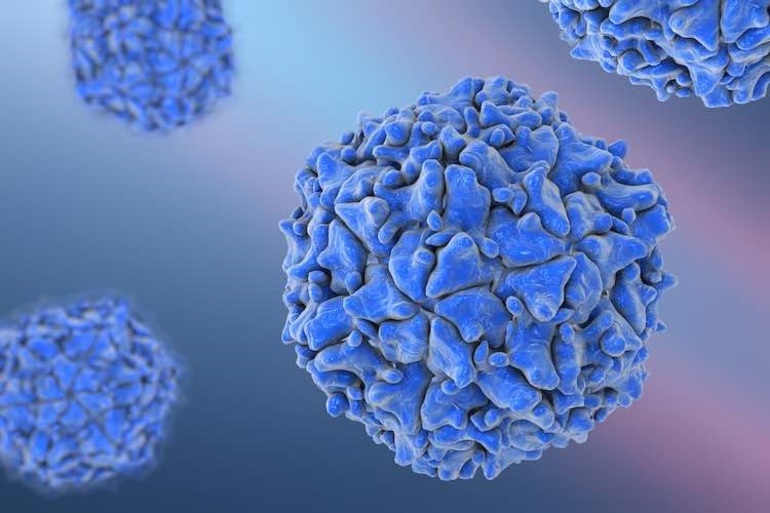
Форму объемного додекаэдра имеют в природе различные объекты. К ним относятся:

В структуре ДНК наблюдается четкая связь. Спираль в виде двойной нити сформирована по схеме двухстороннего соответствия: после икосаэдра идет додекаэдр, затем снова икосаэдр и т. д.

Таким образом, еще с древности ученые доказывали, что в основе структуры дезоксирибонуклеиновой кислоты человека лежат священные правила геометрии и прочие невообразимые взаимосвязи. Работа над доказательством некоторых из них ведется и по сей день.

В древние времена о додекаэдре говорить вообще не было принято, а тем более упоминать вслух. Фигура считалась священной, так как, по мнению ученых, она представляет собой высшую форму человеческого сознания и расположена на внешнем краю энергетического пространства. Философы утверждают, что все человечество живет внутри огромного додекаэдра, заключающего в себе целую Вселенную. Он является завершающей фигурой в геометрии.

Геометрические свойства

Древние мудрецы утверждали: «Чтобы понять невидимое, внимательно смотри на видимое». В сакральных науках додекаэдр считается самым мощным и интересным многогранником. Впервые объемный двенадцатигранник был сделан и построен древнегреческим ученым Теэтетом в IV веке до нашей эры.

Фигура состоит из следующих элементов:

В додекаэдре насчитывается 15 осей симметрии с основным их центром. Каждая из них проходит посередине параллельных ребер, которые размещены при этом параллельно.

Любая из 15 плоскостей симметрии также проходит во всех гранях через середину и вершину противоположно расположенного ребра.

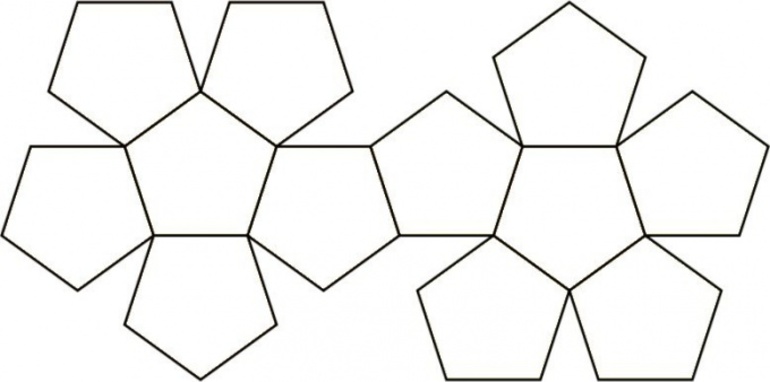
Чтобы понять, что собой представляет этот геометрический элемент, можно сделать развертку додекаэдра. Так более понятно выглядит его площадь. Кроме того, именно по этой схеме можно пошагово сделать фигуру самостоятельно из бумаги или картона, начертив предварительный шаблон с небольшими припусками для загибов.

На чертеже важно правильно определить линии сгибов. При этом немаловажно перед склеиванием знать, какой оттенок материала будет использован. По мнению древнегреческого философа Платона, додекаэдр не относится к известным земным элементам (Огонь, Вода, Земля) и поэтому ассоциируется с пустотой. Такая фигура делается из бумаги желтого цвета.

Развертка также может быть цветной. Первый классический вариант сборки — фигура с гранями, каждая из которых имеет свой оттенок. Второй способ — использование повторяющихся цветов, но они не могут граничить друг с другом.

Додекаэдр, ассоциирующийся с формой кристалла, имеет следующие характерные для него свойства и элементы симметрии:

Идея определения симметрии проста и интересна: если внутри кристалла вообразить ось, а потом вокруг нее повернуть фигуру на определенный угол, то элемент сам с собой совпадет. Это не свойственно никаким другим геометрическим фигурам.

Сфера применения

Благодаря своим свойствам додекаэдр широко используется в современной жизни в различных отраслях. Симметрия и правильная форма делают эту геометрическую фигуру незаменимой как в быту, так и в промышленности или науке.

Правильная схема додекаэдра используется:

Во время раскопок в XVIII веке на территории европейских стран были обнаружены подозрительные предметы, напоминающие по форме додекаэдры. Они были изготовлены из чистой бронзы и имели полое пространство внутри. Во всех гранях были отверстия с разным диаметром.

Таких объектов найдено более сотни, но ученым так и не удалось понять и догадаться, для чего они предназначались.

Находки датируются III—II вв. еком до наступления нашей эры, обнаружены на территории Франции, Германии, Италии, Испании и многих других стран. Если прислушаться к одной из версий, эти предметы использовались как подсвечники, так как внутри обнаружены восковые частички. Согласно другому предположению, это были древние календари, которые подсказывали оптимальное время посадки культур. Третья версия указывает на то, что объемные многогранники использовались как крепление для военного римского штандарта. Какой из фактов достоверный, неизвестно.

В качестве памятника архитектуры малый усеченный додекаэдр установлен в городе Обнинске около здания ДОСААФ. Сегодня это заброшенный объект, неизвестно даже, почему он здесь установлен и кто его автор. Однако точно определено, что появилась фигура еще при Советском Союзе.

Сакральное значение

Значение додекаэдра в сакральной геометрии обусловлено его совершенной формой. Эта наука объединяет совокупность дисциплин, которые обнаруживают и приписывают определенные качества различным фигурам и элементам, основываясь на их свойствах.

Идеальные пропорции способны привести в гармонию все окружающее пространство и находящиеся в нем тела. Энергия распределяется равномерно. Многогранник идеально подходит для медитативной практики, считается, что он выполняет функцию проводника и обеспечивает переход сознания в другую реальность. Специалисты приписывают фигуре способность мгновенно снимать усталость и стресс, улучшать память и повышать концентрацию внимания.

В первую очередь нужно обратить внимание на то, сколько вершин у додекаэдра. Их количество и взаимное расположение символизируют гармонию и уравновешенность.

Для додекаэдра характерны 3 звездчатые формы. В него можно вписать куб, в результате чего стороны вписанной фигуры станут диагоналями двенадцатигранника.

Если вместо пятиугольных граней использовать звезды, то ребра исчезнут, и образуется пространство из пересекающихся пяти кубов. Эти и многие другие удивительные свойства элемента делают его наиболее необычным и загадочным, не похожим ни на одну геометрическую фигуру.

Источник

Додекаэдр

Математические характеристики додекаэдра

Додекаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы додекаэдра

Сфера может быть вписана внутрь додекаэдра.

Радиус вписанной сферы додекаэдра

Площадь поверхности додекаэдра.

Для наглядности площадь поверхности додекаэдра можно представить в виде площади развёртки.

Площадь поверхности можно определить как площадь одной из сторон додекаэдра (это площадь правильного пятиугольника) умноженной на 12. Либо воспользоваться формулой:

Объем додекаэдра определяется по следующей формуле:

Вариант развертки

Древнегреческий философ Платон по одной из версий не относил додекаэдр ни к одному из земных элементов, а по другой из версий ассоциировал додекаэдр с эфиром (пустотой). Для построения модели этого правильного многогранника мы выбрали желтый цвет.

Заметим, что это не единственный вариант развертки.

Кроме того, существуют два классических варианта окраски многогранника, когда каждая из соседних граней окрашена в свой цвет. Либо используется определенное количество цветов раскраски, причем одинаковые цвета не граничат друг с другом.

Представляем Вашему вниманию два варианта окраски додекаэдра с использованием шести и четырех цветов.

Источник

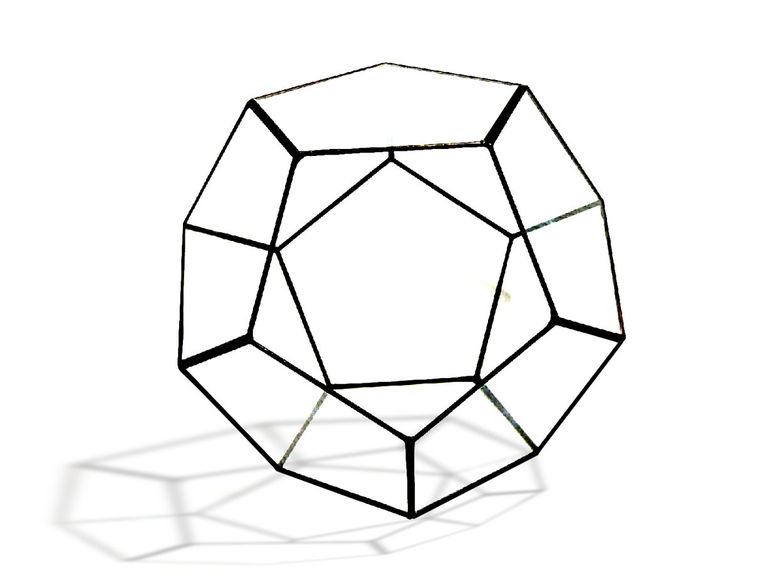
Додекаэдр — свойства, вид и структура двенадцатигранника

Додекаэдр — это двенадцатигранник, представляющий собой правильное геометрическое тело, образованное гранями в виде пятиугольников. Он относится к многогранникам, входит в группу платоновых тел, имеет особые характеристики, отличающие его от других математических элементов. Этой фигуре было дано название еще в Древней Греции. Благодаря особым свойствам объект нашел применение во многих сферах жизни человека.

Фигура в природе

Правильный многогранник считается шаблоном, привлекает безупречным совершенством формы и абсолютной симметричностью сторон. Природной моделью геометрической фигуры является кристалл пирита (FeS — колчедан сернистый).

Форму объемного додекаэдра имеют в природе различные объекты. К ним относятся:

В структуре ДНК наблюдается четкая связь. Спираль в виде двойной нити сформирована по схеме двухстороннего соответствия: после икосаэдра идет додекаэдр, затем снова икосаэдр и т. д.

Таким образом, еще с древности ученые доказывали, что в основе структуры дезоксирибонуклеиновой кислоты человека лежат священные правила геометрии и прочие невообразимые взаимосвязи. Работа над доказательством некоторых из них ведется и по сей день.

В древние времена о додекаэдре говорить вообще не было принято, а тем более упоминать вслух. Фигура считалась священной, так как, по мнению ученых, она представляет собой высшую форму человеческого сознания и расположена на внешнем краю энергетического пространства. Философы утверждают, что все человечество живет внутри огромного додекаэдра, заключающего в себе целую Вселенную. Он является завершающей фигурой в геометрии.

Геометрические свойства

Древние мудрецы утверждали: «Чтобы понять невидимое, внимательно смотри на видимое». В сакральных науках додекаэдр считается самым мощным и интересным многогранником. Впервые объемный двенадцатигранник был сделан и построен древнегреческим ученым Теэтетом в IV веке до нашей эры.

Фигура состоит из следующих элементов:

В додекаэдре насчитывается 15 осей симметрии с основным их центром. Каждая из них проходит посередине параллельных ребер, которые размещены при этом параллельно.

Любая из 15 плоскостей симметрии также проходит во всех гранях через середину и вершину противоположно расположенного ребра.

Чтобы понять, что собой представляет этот геометрический элемент, можно сделать развертку додекаэдра. Так более понятно выглядит его площадь. Кроме того, именно по этой схеме можно пошагово сделать фигуру самостоятельно из бумаги или картона, начертив предварительный шаблон с небольшими припусками для загибов.

На чертеже важно правильно определить линии сгибов. При этом немаловажно перед склеиванием знать, какой оттенок материала будет использован. По мнению древнегреческого философа Платона, додекаэдр не относится к известным земным элементам (Огонь, Вода, Земля) и поэтому ассоциируется с пустотой. Такая фигура делается из бумаги желтого цвета.

Развертка также может быть цветной. Первый классический вариант сборки — фигура с гранями, каждая из которых имеет свой оттенок. Второй способ — использование повторяющихся цветов, но они не могут граничить друг с другом.

Додекаэдр, ассоциирующийся с формой кристалла, имеет следующие характерные для него свойства и элементы симметрии:

Идея определения симметрии проста и интересна: если внутри кристалла вообразить ось, а потом вокруг нее повернуть фигуру на определенный угол, то элемент сам с собой совпадет. Это не свойственно никаким другим геометрическим фигурам.

Сфера применения

Благодаря своим свойствам додекаэдр широко используется в современной жизни в различных отраслях. Симметрия и правильная форма делают эту геометрическую фигуру незаменимой как в быту, так и в промышленности или науке.

Правильная схема додекаэдра используется:

Во время раскопок в XVIII веке на территории европейских стран были обнаружены подозрительные предметы, напоминающие по форме додекаэдры. Они были изготовлены из чистой бронзы и имели полое пространство внутри. Во всех гранях были отверстия с разным диаметром.

Таких объектов найдено более сотни, но ученым так и не удалось понять и догадаться, для чего они предназначались.

Находки датируются III—II вв. еком до наступления нашей эры, обнаружены на территории Франции, Германии, Италии, Испании и многих других стран. Если прислушаться к одной из версий, эти предметы использовались как подсвечники, так как внутри обнаружены восковые частички. Согласно другому предположению, это были древние календари, которые подсказывали оптимальное время посадки культур. Третья версия указывает на то, что объемные многогранники использовались как крепление для военного римского штандарта. Какой из фактов достоверный, неизвестно.

В качестве памятника архитектуры малый усеченный додекаэдр установлен в городе Обнинске около здания ДОСААФ. Сегодня это заброшенный объект, неизвестно даже, почему он здесь установлен и кто его автор. Однако точно определено, что появилась фигура еще при Советском Союзе.

Сакральное значение

Значение додекаэдра в сакральной геометрии обусловлено его совершенной формой. Эта наука объединяет совокупность дисциплин, которые обнаруживают и приписывают определенные качества различным фигурам и элементам, основываясь на их свойствах.

Идеальные пропорции способны привести в гармонию все окружающее пространство и находящиеся в нем тела. Энергия распределяется равномерно. Многогранник идеально подходит для медитативной практики, считается, что он выполняет функцию проводника и обеспечивает переход сознания в другую реальность. Специалисты приписывают фигуре способность мгновенно снимать усталость и стресс, улучшать память и повышать концентрацию внимания.

В первую очередь нужно обратить внимание на то, сколько вершин у додекаэдра. Их количество и взаимное расположение символизируют гармонию и уравновешенность.

Для додекаэдра характерны 3 звездчатые формы. В него можно вписать куб, в результате чего стороны вписанной фигуры станут диагоналями двенадцатигранника.

Если вместо пятиугольных граней использовать звезды, то ребра исчезнут, и образуется пространство из пересекающихся пяти кубов. Эти и многие другие удивительные свойства элемента делают его наиболее необычным и загадочным, не похожим ни на одну геометрическую фигуру.

Источник

Додекаэдр

Додекаэдр
Тип	Правильный многогранник
Грань	Правильный пятиугольник
Граней	12
Рёбер	30
Вершин	20
Граней при вершине	3
Длина ребра
Площадь поверхности
Объём
Радиус описанной сферы
Радиус вписанной сферы
Группа симметрии	Икосаэдрическая (Ih)
Двойственный многогранник	икосаэдр

Додека́эдр (от греч. δώδεκα — двенадцать и εδρον — грань) — двенадцатигранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников.

Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра). Сумма плоских углов при каждой из 20 вершин равна 324°.

Содержание

Основные формулы

Если за длину ребра принять , то площадь поверхности додекаэдра:

Радиус описанной сферы:

Радиус вписанной сферы:

Свойства

Элементы симметрии додекаэдра

Каждая из осей проходит через середины противолежащих параллельных ребер.

Тела в форме додекаэдра

Интересные факты

Примечания

См. также

Полезное

Смотреть что такое «Додекаэдр» в других словарях:

ДОДЕКАЭДР — (греч., от dodeka двенадцать, и hedra основание). Двенадцатигранник. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ДОДЕКАЭДР геометрич. тело, ограниченное двенадцатью правильными, т. е. равносторонними… … Словарь иностранных слов русского языка

додекаэдр — двенадцатигранник, многогранник Словарь русских синонимов. додекаэдр сущ., кол во синонимов: 2 • двенадцатигранник (4) • … Словарь синонимов

ДОДЕКАЭДР — (от греческого dodeka двенадцать и hedra грань), один из пяти типов правильных многогранников, имеющий 12 пятиугольных граней, 30 ребер и 20 вершин, в каждой из которых сходятся 3 ребра … Современная энциклопедия

ДОДЕКАЭДР — (от греч. dodeka двенадцать и hedra грань) один из пяти типов правильных многогранников; имеет 12 граней (пятиугольных), 30 ребер, 20 вершин (в каждой сходятся 3 ребра) … Большой Энциклопедический словарь

ДОДЕКАЭДР — муж., греч. двенадцатигранник; тело, ограниченное двенадцатью правильными пятиугольниками: оно образуется из шара, срезкою отсеков. | Гранка (кристалл) о двенадцати природных гранях. Додекаэдрический, двенадцатигранный. Толковый словарь Даля. В.И … Толковый словарь Даля

ДОДЕКАЭДР — в кристаллографии двенадцатигранник. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия

додекаэдр — додекаэдр. Произносится [додэкаэдр] … Словарь трудностей произношения и ударения в современном русском языке

додекаэдр — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN dodecahedron … Справочник технического переводчика

Додекаэдр — (от греческого dodeka двенадцать и hedra грань), один из пяти типов правильных многогранников, имеющий 12 пятиугольных граней, 30 ребер и 20 вершин, в каждой из которых сходятся 3 ребра. … Иллюстрированный энциклопедический словарь

Додекаэдр — (от греч. dódeka двенадцать и hédra грань) один из пяти типов правильных Многогранников. Д. имеет 12 граней (пятиугольных), 30 рёбер, 20 вершин (в каждой вершине сходятся 3 ребра). Если а длина ребра Д., то его объём … … Большая советская энциклопедия

Источник

Правильный додекаэдр

Связанные понятия

Полуправильные многогранники — в общем случае это различные выпуклые многогранники, которые, не являясь правильными, имеют некоторые их признаки, например: все грани равны, или все грани являются правильными многоугольниками, или имеются определённые пространственные симметрии. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

Многогранник размерности 3 и выше называется изоэдральным или гране транзитивным, если все его грани одинаковы. Точнее сказать, все грани должны быть не просто конгруэнтны, а должны быть транзитивны, то есть должны прилежать в одной и той же орбите симметрии. Другими словами, для любых граней A и B должна существовать симметрия всего тела (состоящая из вращений и отражений), которая отображает A в B. По этой причине выпуклые изоэдральные многогранники имеют формы правильных игральных костей.

В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.

Пра́вильный двадцатичетырёхъяче́йник, или просто двадцатичетырёхъяче́йник, или икоситетрахор (от др.-греч. εἴκοσι — «двадцать», τέτταρες — «четыре» и χώρος — «место, пространство»), — один из правильных многоячейников в четырёхмерном пространстве.

Пра́вильный шестнадцатияче́йник, или просто шестнадцатияче́йник — один из правильных многоячейников в четырёхмерном пространстве. Известен также под другими названиями: гексадекахор (от др.-греч. ἕξ — «шесть», δέκα — «десять» и χώρος — «место, пространство»), четырёхмерный гиперокта́эдр (поскольку является аналогом трёхмерного октаэдра), четырёхмерный кокуб (поскольку двойственен четырёхмерному гиперкубу), четырёхмерный ортоплекс.

Правильные четырёхмерные многогранники являются четырёхмерными аналогами правильных многогранников в трёхмерном пространстве и правильных многоугольников на плоскости.

Источник