что такое длина сторон

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

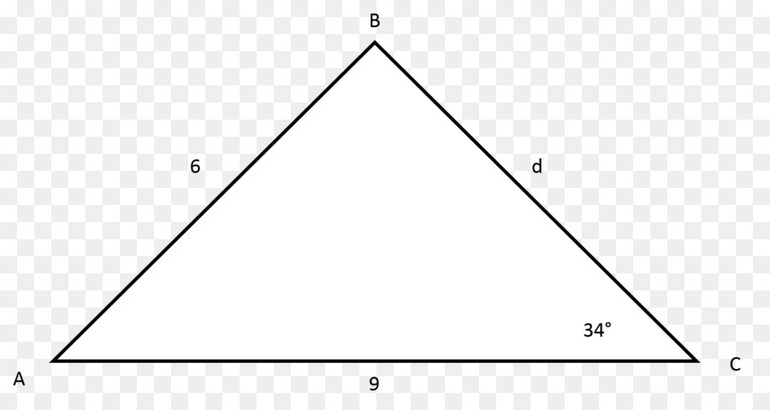
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

Формула длины через сторону и два угла (по теореме синусов), ( a):

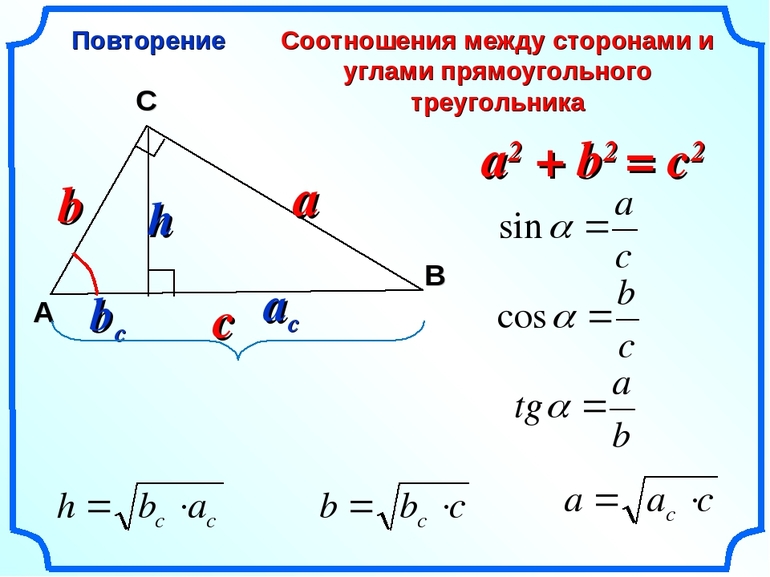
2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

Формулы длины стороны (основания), (b ):

4. Найти длину высоты треугольника

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Источник

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

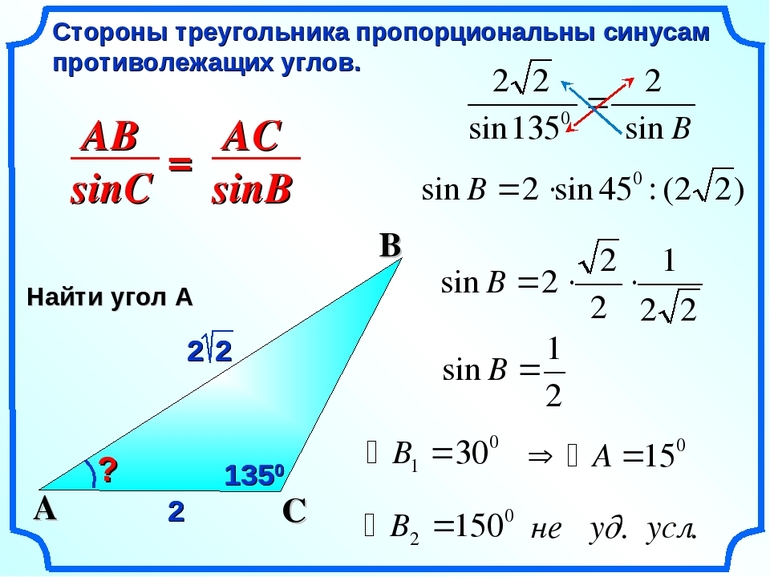
Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

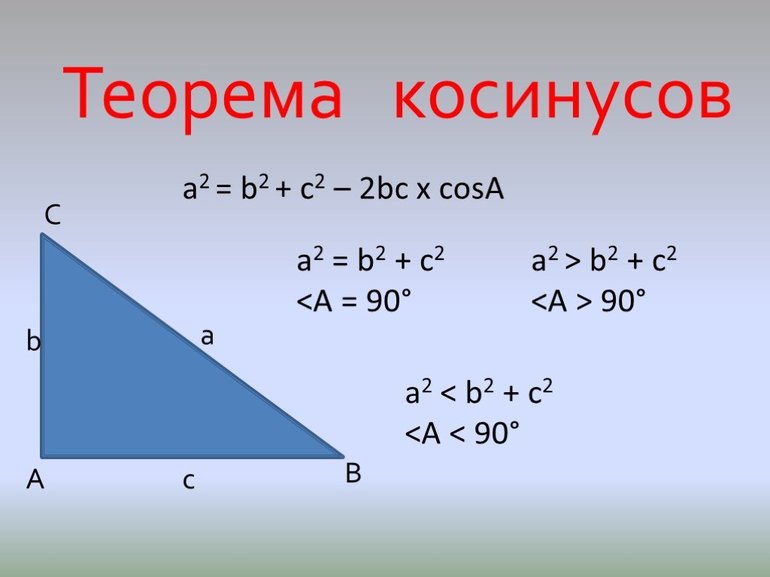
Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Треугольник — определение и основные свойства и виды треугольника

Что такое треугольник знают дети уже в самом младшем возрасте, они умеют находить треугольник среди множества геометрических фигур. Но вот уже в школе по геометрии проходят треугольник и надо не просто узнавать треугольник, но и дать определение этому понятию.

Определение треугольника

Треугольник — это геометрическая фигура, окруженная тремя отрезками прямой (конечные точки каждых двух смежных отрезков соединены или перекрываются), называется треугольником. Точки пересечения отрезков называются вершинами треугольника, а сами отрезки между двумя соседними вершинами треугольника называются сторонами треугольника.

Посмотрите на треугольник на рисунке.

У него три вершины — , , и три стороны , и . У каждого треугольника есть имя — это имя образовано вершинами треугольника. Наш треугольник зовут ([а-бэ-цэ]). А треугольник на вот этом рисунке

будут звать ([эм-эн-ка]).

По правилам математической грамотности треугольник, как и любой другой многоугольник, следует называть, начиная с левого нижнего угла и называя все вершины по часовой стрелке.

В треугольнике можно провести особенные стороны — высоту, медиану и биссектрису. Начнем с высоты треугольника.

Высота треугольника

В каждом треугольнике можно провести три высоты. Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на противолежащую этой вершине сторону.

Например, в треугольнике , высотой будет отрезок .

А теперь проведем из каждой вершины по высоте — получим три высоты — больше провести высот нельзя.

В этом треугольнике три высоты , , .

Про биссектрисы и медианы поговорим в других статьях. Сейчас же давайте с вами рассмотрим каким бывает треугольник.

Виды треугольника

Виды треугольника могут быть по углам и по сторонам. То есть в первом случае вид треугольника зависит от того, какие в этом треугольнике углы, а во втором случае — какие в этом треугольнике стороны.

Виды треугольников по углам

В зависимости от того, все ли углы в треугольнике острые или есть тупой угол или угол, равный , треугольник бывает остроугольным, тупоугольным или прямоугольным.

Посмотрите на рисунки — перед вами три основных вида треугольника:

Виды треугольников по сторонам

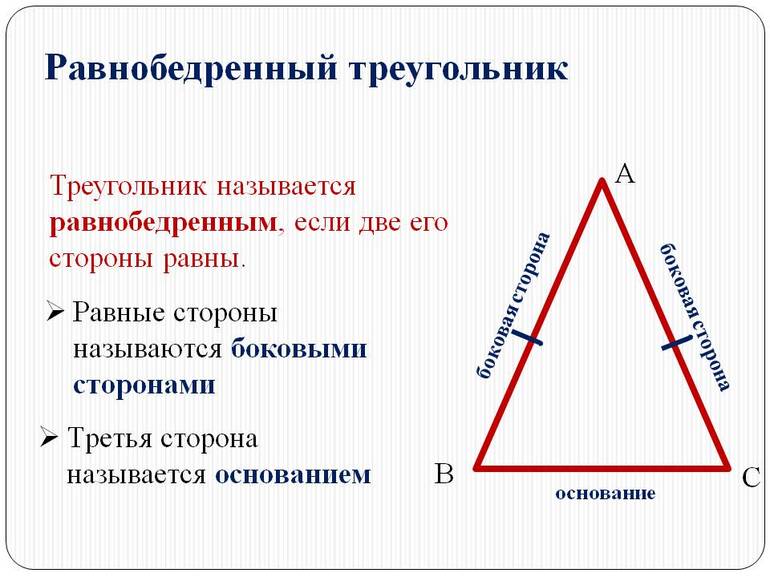
Если у треугольника все стороны равны, то такой треугольник называют равносторонним или правильным. Если у треугольника равны только две стороны, то такой треугольник называют равнобедренным.

На рисунке показаны равносторонний и равнобедренный треугольники.

Свойства сторон треугольника

Треугольник имеет важные свойства и характеристики.

Устойчивость — это важное свойство треугольника, оно вам еще пригодится в курсе физики. Но вначале мы с ним знакомимся на уроках геометрии.

Треугольник устойчив на любой своей стороне — то есть чтобы вывести его из состояния равновесия надо приложить силу.

Свойства сторон: разница между любыми двумя сторонами треугольника меньше, чем третья сторона, а также любая сторона треугольника меньше, чем сумма двух других сторон. То есть:

Например, пусть наш треугольник имеет длины двух сторон , а см. В каком диапазоне будет размер третьей стороны треугольника?

Решение: согласно свойству сторон треугольника, получим:

Таким образом, третья сторона треугольника может быть в диапазоне от 4 до 10 см. Или в целых числах ее длина может быть 5, 6, 7, 8 или 9 см.

Правило существования треугольника

Используя свойство сторон треугольника мы можем определить существует ли треугольник с определенными сторонами.

Для проверки сложите длины самых коротких сторон и если сумма их больше длины самой большой стороны, тогда треугольник существует.

Например, существует ли треугольник с длинами сторон 3, 7 и 15 см?

Решение: проверим по свойству сторон треугольника: складываем две самые короткие стороны 3 и 7 см: 3+7=10, а 10 7 — треугольник с такими длинами сторон существует.

Свойство углов в треугольнике

Сумма всех углов в треугольнике равна .

Согласно этому свойству мы всегда можем, зная два угла в треугольнике, найти его третий угол. В прямоугольном треугольнике сумма двух острых углов всегда равна .

Например, пусть известно, что в треугольнике , , , нужно найти .

Так как сумма углов в треугольнике равна , то находим:

.

Ответ: .

Элементы композиции

Многие школьники спрашивают — а зачем нам знать про треугольник, как это может пригодиться в обычной жизни? Треугольник — простая фигура из которой можно составить более сложные. Это используется во многих сферах жизни, например, вы можете эргономично убирать в своей комнате, или красиво выкладывать бутерброды. Например, из двух равных треугольников можно составить параллелограмм.

А из двух равных прямоугольных треугольником — прямоугольник или квадрат. Два треугольника могут образовать трапецию, так как на рисунке. А вот какую фигурку можно смоделировать для программируемой игры — она вся сделана из треугольников:

Мы, рассмотрели самые важные свойства треугольника, и в дальнейшем изучим еще больше разных интересных свойств, закономерностей. Несмотря на свою простоту, треугольник таит в себе много загадок и открытий.

Источник

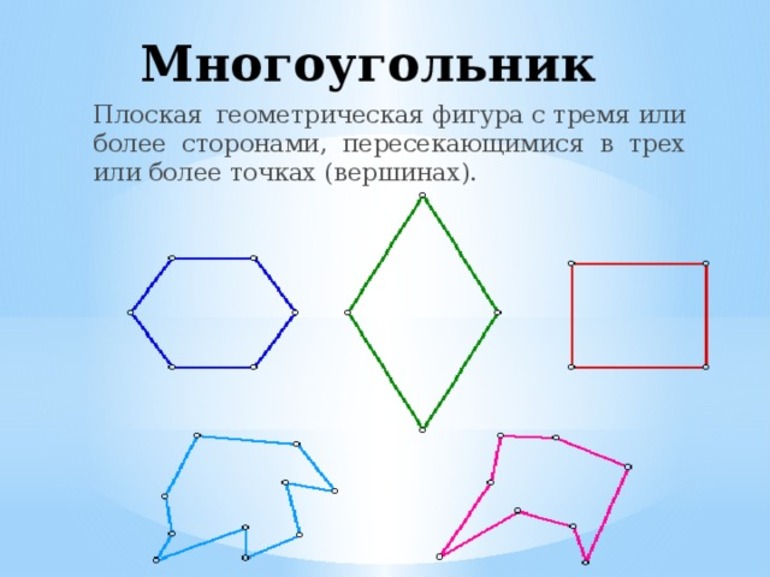
Многоугольник с тремя сторонами

Прежде чем рассматривать задачу о том, как проверить, существует ли треугольник, следует подробно изучить эту фигуру. Согласно общепринятому определению, любой замкнутый многоугольник на плоскости, который состоит из трех отрезков, пересекающихся своими концами друг с другом, является треугольником. Эта фигура имеет две группы образующих ее элементов:

Сторонами являются три отрезка, длины которых могут быть либо известны по условию задачи, либо их предстоит рассчитать. Касательно вершин следует сказать, что у любого рассматриваемого многоугольника их три. Каждую принято обозначать одной латинской буквой, например, A, B, C и так далее. Поскольку два отрезка пересекаются в вершине, то они образуют некоторый угол. Их у фигуры три, поэтому становится понятным, откуда происходит название «треугольник».

Типы фигуры

Их классификация является достаточно развитой. В ее основу положены принципы взаимоотношения длин сторон друг с другом, а также численные значения углов. В общем случае в геометрии рассматривают следующие типы треугольников:

Два основных свойства

В некоторых геометрических задачах можно встретить проблемы, которые формулируются так: можно ли построить треугольник со сторонами a, b, c, если известны их длины. Либо другой тип задач, которые предполагают знание некоторых сторон и углов, и требуют определить возможность существования такой фигуры.

Ответ на все эти проблемы заключается всего в одном слове: либо «да» и такой треугольник действительно существует, либо «нет» и из заданных элементов его построить не представляется возможным. Разобраться со всеми этими задачами поможет знание двух главных свойств, которые всегда справедливы для треугольников любых типов:

Оба свойства с успехом можно и необходимо применять, чтобы проверить или узнать возможность существования того или иного треугольника. Важно понимать, что невыполнение любого из свойств говорит о невозможности построения рассматриваемой фигуры.

Вопрос вырождения

В свете изучения возможности существования треугольников важно рассмотреть вопрос их вырождения. В математике придумали универсальную формулу, которая позволяет оценить качество треугольника. Она имеет вид:

Каждый из трех множителей числителя является положительным числом, что следует из главного свойства треугольников. Величина качества CT является положительной и лежит в пределах значений 0 и 1. Возможны следующие случаи:

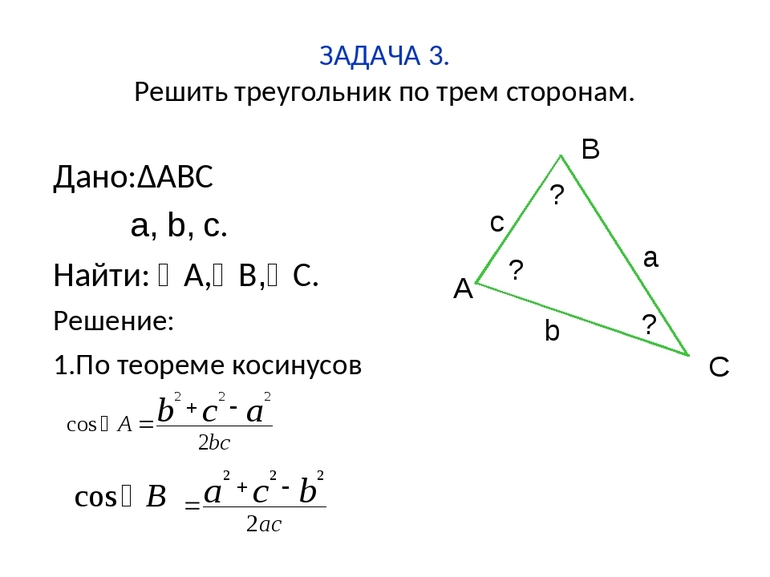
Теорема косинусов

Чтобы решать задачи на треугольники, недостаточно знать лишь главные их свойства. Последние позволяют лишь дать качественный, но не количественный ответ. Теорем и формул для рассматриваемых многоугольников известно много (синусов, Пифагора, медиан, Герона и др.). Однако, теорема косинусов является одной из основополагающих, поскольку позволяет по двум сторонам и углу определить значение длины третьей стороны (справедливости ради следует отметить, что теорема синусов является не менее важной, поскольку она по двум углам и стороне позволяет вычислить неизвестные стороны).

Соответствующее выражение имеет следующий вид:

c 2 = a 2 + b 2 — 2*a*b*cos (α).

Решение задач

Для закрепления полученных знаний полезно привести пару примеров решения типичных геометрических задач с треугольниками, в которых нужно будет либо дать качественный ответ, либо получить некоторое количественное значение.

Первая задача требует получить качественный ответ. Пусть имеется треугольник со сторонами 1, 2, 4. Существует ли такая фигура, требуется выяснить.

Для решения этой проблемы абсолютно неважно измеряются стороны в метрах, в сантиметрах, в дюймах или в других величинах. Важно лишь взаимоотношение между ними. Для каждой из длин отрезков следует проверить свойство существования рассматриваемой фигуры. Если получится хотя бы одна ложь, то треугольник построить нельзя:

Таким образом, для определения возможности существования того или иного треугольника на плоскости необходимо проверить тот факт, что каждая из его сторон имеет меньшую длину, чем сумма двух других отрезков. Теорема косинусов является удобным инструментом для определения количественных характеристик рассматриваемого типа фигур.

Источник