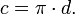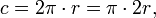что такое длина окружности определение
Длина окружности
6 класс, 9 класс, ЕГЭ/ОГЭ
Как найти длину окружности через диаметр
Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:
π— число пи — математическая константа, равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, равное 3,14
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, равное 3,14
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она всегда равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен 
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Длина окружности
Длина окружности — это длина закрытой кривой. Определение окружности в статье Окружность.
Длина окружности вычисляется из диаметра по формуле::
Или из половины диаметра, радиуса:
где r — это радиус, d — диаметр круга, а π (греческая буква пи), которая является математической постоянной, отношением длины окружности к ее диаметру (значение пи, первые цифры: 3.141 592 653 589 793).
Смотреть что такое «Длина окружности» в других словарях:
длина окружности резервуара — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN tank circumference … Справочник технического переводчика
длина окружности совокупность известных операций — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN circuit … Справочник технического переводчика
ДЛИНА — ДЛИНА, длины, мн. нет, жен. Протяжение линии, плоскости, тела в том направлении, в котором две крайние точки (линии, плоскости, тела) лежат на наибольшем расстоянии одна от другой. Предметы измеряются в длину, ширину и высоту. Длина стола. Меры… … Толковый словарь Ушакова
длина — ы/, только ед., ж. 1) Протяжение в том направлении, в котором две крайние точки линии, плоскости, тела лежат на наибольшем расстоянии друг от друга. Мера длины. Лыжи длиной в два метра. Измерить площадку в длину и в ширину. Синонимы: расстоя/ние… … Популярный словарь русского языка
Длина кривой — (или, что то же, длина дуги кривой) в метрическом пространстве числовая характеристика протяжённости этой кривой[1]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой… … Википедия
Длина шкалы — Расстояние между крайними отметками шкалы, отсчитанное по дуге окружности или по прямой линии, проходящей через середины наименьших отметок Источник: ГОСТ 2405 88: Манометры, вакуумметры, мановакуумметр … Словарь-справочник терминов нормативно-технической документации
Длина дуги — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия
Длина дуги кривой — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия
длина — 3.1 длина (length) l: Наибольший линейный размер лицевой грани измеряемого образца. Источник: ГОСТ Р ЕН 822 2008: Изделия теплоизоляционные, применяемые в строительстве. Методы измерения длины и ширины … Словарь-справочник терминов нормативно-технической документации
Длина — числовая характеристика протяжённости линий. В разных случаях понятие Д. определяется различно. 1) Д. отрезка прямой расстояние между его концами, измеренное каким либо отрезком, принятым за единицу Д. 2) Д. ломаной сумма Д. её звеньев.… … Большая советская энциклопедия
Длина окружности
Возьмем циркуль. Установим ножку циркуля с иглой в точку « O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Диаметр окружности обозначается буквой « D ». На рисунке выше — это отрезок « BC ».
На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение « D = 2R ».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»).
π ≈ 3,14…
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2 π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Определите диаметр окружности, если её длина равна 56,52 дм. ( π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки « A » и « B ». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга « AB » и черная дуга « AB ». Точки « A » и « B » называют концами дуг.
Соединим точки « A » и « B » отрезком. Полученный отрезок называют хордой.
Точки « A » и « B » делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга « AB ».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.
Что такое длина окружности?
Кроме того, какова длина круга?
Диаметр длина линии, проходящей через центр, которая касается двух точек на краю круга.
При этом, что такое окружность круга диаметром 10 см?
Итак, окружность круга диаметром 10 см равна 31.4 см.
Также нужно знать, что такое формула длины? Формулы для длины дуги
| Формула длины дуги (если θ в градусах) | s = 2 π r (θ / 360 °) |
|---|---|
| Формула длины дуги (если θ в радианах) | s = ϴ × r |
| Формула длины дуги в интегральной форме | s = int ^ _asqrt <1+ (гидроразрыв |
Как найти окружность прямой?
Каков диаметр 9-дюймового круга?
| Диаметр | in 2 | ft 2 |
|---|---|---|
| 9.0 д | 63.62 | 0.4418 |
| 9.1 д | 65.04 | 0.4517 |
| 9.2 д | 66.48 | 0.4616 |
| 9.3 д | 67.93 | 0.4717 |
Каков радиус 35-дюймового круга?
Какова площадь круга радиусом 35 дюймов?
| Результат: площадь круга радиусом 35 равна 3848 | |
|---|---|
| Формулы: | |
| г = 35 г = 70 С = 220 | A = πr 2 = π (d2) 2 А = С 2 4π π = 3.1415 A = площадь C = окружность или периметр r = радиус, d = диаметр |
Какая оценка ближе всего к окружности круга радиусом 10 см?
2π10 =20π см или около 62.8 см.
Какова окружность круга диаметром 14 см?
Диаметр = 14 см. Итак, радиус = 14/2 см = 7 см. Окружность = 2 пи р. Итак, окружность = 2 × 7 × 22/7 = 44cm.
Какой диаметр 10 см?
| Диаметр | Длина окружности | Приблизительный |
|---|---|---|
| 10 см | 31.4 см | 10 см X 3 = 30 |
| 2 см | 6.24 см | 2 см X 3 = 6 |
| 5 см | 15.7 см | 5 см х 3 = 15 см |
Какова формула периметра?
Периметр, площадь и объем
Что такое формула площади?
ЧТО ТАКОЕ формула линзы?
Окружность: Окружность круга равна расстояние вокруг него. Диаметр: любая прямая линия, проходящая через центр круга до двух точек по периметру. Радиус: любая прямая линия, которая начинается в центре круга и заканчивается по периметру.
Как определить диаметр?
Если вам дана площадь круга, диаметр будет равен квадратный корень из четырехкратного деления площади на пи (диаметр = √ (4 x площадь) / пи).
Как найти диаметр лески?
Разделите окружность на пи, примерно 3.14, чтобы вычислить диаметр круга. Например, если длина окружности равна 56.52 дюйма, разделите 56.52 на 3.14, чтобы получить диаметр 18 дюймов. Умножьте радиус на 2, чтобы найти диаметр.
Что означает диаметр 9 дюймов?
Какова окружность диаметра 12 дюймов?
Какова окружность круга диаметром 12 дюймов?
| Размер в дюймах | Окружность в дюймах | Площадь в квадратных дюймах |
|---|---|---|
| 12 | 37.700 | 144.000 |
| 12 1/4 | 38.480 | 150.060 |
| 12 1/2 | 39.270 | 156.250 |
| 12 3/4 | 40.060 | 162.560 |
Какова длина круга диаметром 35?
Какова окружность круга диаметром 35 дюйма?
Окружность круга диаметром 35 дюйма.
| 109.96 | дюймов |
|---|---|
| 279.29 | сантиметров |
Какова площадь круга диаметром 6 см?
Какова площадь круга диаметром 6 см?
| Результат: площадь круга диаметром 6 равна 28.27 | |
|---|---|
| Формулы: | |
| г = 3 г = 6 С = 18.9 | A = πr 2 = π (d2) 2 А = С 2 4π π = 3.1415 A = площадь C = окружность или периметр r = радиус, d = диаметр |
Будет ли круг радиусом 10 см иметь ту же длину окружности, что и круг диаметром 20 см?
Радиус составляет половину диаметра. Следовательно, радиус 10 см будет иметь диаметр 20 см, поэтому он будет иметь одинаковую окружность.
Каков радиус круга диаметром 6 см?
Если r = 6 см, длина окружности c = 2π (6) = 12π см, если писать через π. Если вы предпочитаете числовое значение, ответ, округленный до десятых, составит 37.7 см.
Какая длина окружности 14 дюймов?
Окружность 14-дюймового круга равна 43.98 дюймов.
Какова окружность круга диаметром 28 см?
Окружность 87.96 сантиметры равно:
Воспользуйтесь калькулятором длины окружности выше, чтобы найти периметр круга с учетом его диаметра или других параметров.
Что подразумевается под окружностью круга?
В геометрии длина окружности (от латинского слова «круг», что означает «переносить») равна периметр круга или эллипса. То есть окружность будет длиной дуги окружности, как если бы она была раскрыта и выпрямлена до отрезка линии.
Урок 25 Бесплатно Длина окружности и площадь круга
На этом уроке мы рассмотрим одни из самых древнейших геометрических фигур: окружность и круг.
Определим, какими элементами характеризуются круг и окружность, в чем сходство и различие этих фигур.
Узнаем, как рассчитать длину окружности и площадь круга.
Окружность и круг
Мы часто встречаем такие понятия, как окружность и круг.
Давайте попробуем разобраться, что называют окружностью, а что кругом.
Центр окружности— это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки окружности, ее обозначают обычно заглавной буквой О.
Свои имена окружность и круг приобрели не сразу.
В древние времена специальных названий для этих фигур не существовало. Люди пытались описать различные геометрические формы, сравнивая объекты. Например, говоря про что-то круглое, говорили: «такой, как солнце» или «такой, как орех» и т.п.
Только в Древней Греции окружность и круг приобрели себе свои названия.
Круг всегда привлекал к себе внимание как самая простая фигура из кривых, но самая загадочная.
У меня есть дополнительная информация к этой части урока!
Древние греки считали круг и окружность символом бесконечности и совершенства. Поражало то, что в каждой своей точке окружность устроена одинаково, представляя собой бесконечную линию, которая движется сама по себе.
У древних славян еще за долго до христианства круг был символом солнца.
Символика круга в различных религиях сопоставляется с целостностью, вечностью и бесконечной мудростью.
У буддистов круг символизирует единство внутреннего и внешнего мира.
В христианстве круг служит эталоном божественного и духовного совершенства.
В живой и неживой природе круги и окружности встречаются как на макроуровнях, так и на микроуровнях. Например, движение электронов вокруг атомного ядра; вращение планет вокруг солнца; распространение волн на воде от упавшего груза; образование солнечного и лунного гало; срез дерева; зрачок глаза у человека и многое другое.
Рассмотрим подробней элементы, характерные для окружности.
Радиус окружности— это отрезок, соединяющий центр окружности и любую другую точку, расположенную на линии окружности.
С латинского радиус (radius)- луч, спица колеса. Радиус не сразу приобрел себе такое название.
Слово радиус впервые встречается в 1569 году у французского ученого П. Рамуса, а общепризнанным становится к концу XVII века.
Радиус обозначается маленькой латинской буквой (r) или заглавной (R).
В окружности можно провести столько же радиусов, сколько точек имеет линия окружности; все эти радиусы равны.
Обычно диаметр обозначают латинской маленькой буквой d или заглавной D.
По величине диаметр равен двум радиусам, лежащим на одной прямой.
d = 2r
Следовательно, радиус- это половина диаметра.
r = d: 2
Пример 1
Радиус окружности равен 6 см.
Чему равен диаметр окружности?
r = 6 см
Решение:
d = 2r
d = 2r= 2*6 = 12 (см) диаметр окружности
Ответ: d= 12 см
Пример 2
Диаметр окружности равен 12 см.
Чему равен радиус окружности?
d = 12 см
Решение:
r = d : 2
r = 12 : 2 = 6 (см) радиус окружности
Ответ: r = 6 см
У меня есть дополнительная информация к этой части урока!
Образовались две дуги: \(\mathbf<\cup AB\ и\ \cup BA>\)
Отрезок, который соединяет любые две точки на окружности (отрезок секущей), называется хордой.
На рисунке отрезок MN является хордой.
Если хорда проходит через центр окружности, то она является самой большой хордой для этой окружности. По своей сути она является диаметром для данной окружности и делит окружность на две равные дуги.
По мере удаления хорды от центра размеры ее уменьшаются, а дуги делятся на большую и малую.
АВ— самая большая хорда окружности- диаметр окружности.
CD, N1M1, NM, FE— хорды окружности.
Хорды окружности, удаленные на равные расстояния от центра, равны.
Хорды NM и N1M1 равны.
Если две хорды пересекаются в точке, то их отрезки пропорциональны.
Важно отметить, что все рассмотренные элементы окружности одинаковы и для круга.
Пройти тест и получить оценку можно после входа или регистрации
Длина окружности и площадь круга
Давайте выясним, что такое длина окружности и как ее определить.
Представьте, что окружность обернута нитью.
Если разрезать эту нить в некоторой точке и размотать ее, то длина нитки будет равна длине окружности.
Обычно длина окружности обозначается заглавной буквой С
Длина окружности (С) зависит от длины ее диаметра (d)
Обратите внимание на рисунок.
Вы можете заметить, что чем больше диаметр, тем больше длина окружности.
Из этого следует, что длина окружности прямо пропорционально зависит от диаметра окружности.
А значит, для любых окружностей отношение длины окружности (С) к длине диаметра (d) является числом постоянным.
Это число (коэффициент пропорциональности) обозначают греческой буквой \(\mathbf<\pi>\), читается «пи».
С— это длина окружности
d— диаметр окружности
запишем отношение \(\mathbf
отсюда следует, что длина окружности равна
Так как диаметр окружности вдвое больше радиуса d = 2r, получим еще одну формулу для вычисления длины окружности
Число \(\mathbf<\pi>\)- это иррациональное число, т.е. число, которое представлено в виде бесконечной непериодической десятичной дроби.
У меня есть дополнительная информация к этой части урока!
История числа \(\mathbf< \pi>\) насчитывает около 4 тысячелетий.
Одно из первых доказательств древнего существования этого числа \(\mathbf< \pi>\) заключено в папирусе Ахмеса, в одном из старейших задачников (1650 год до н.э.), найденного в Древнем Египте.
В папирусе дано достаточно точное, особенного для того времени, значение числа, равного 3,1605.
Точнее число \(\mathbf< \pi>\) рассчитал древнегреческий математик Архимед. Он приближенно представил значение константы в виде обыкновенной дроби \(\mathbf<\frac <22><7>>\)
Архимеду удалось найти точное приближение числа \(\mathbf< \pi>\) (т.е. узкий числовой промежуток к которому принадлежит число \(\mathbf< \pi>\)).
Пройти тест и получить оценку можно после входа или регистрации
Решения задач по теме «Длина окружности и площадь круга»
Рассмотрим примеры решения задач
Задача 1
Найдите длину окружности, если ее радиус равен 4 см.
Число \(\mathbf<<\pi>>\) округлите до сотых.
r = 4 см
Решение:
Подставив в формулу известные значения радиуса и постоянной \(\mathbf<\pi>\), получим:
Ответ: \(\mathbf
Задача 2
Длина окружности надувного бассейна 15,7м.
Найдите диаметр этого бассейна.
Число \(\mathbf<\pi>\) округлите до сотых.
C = 15,7 м
Решение:
Подставив в формулу известные значения длины окружности и постоянной \(\mathbf<\pi>\), получим:
Ответ: \(\mathbf
Задача 3
Диаметр окружности равен 6 см.
Найдите площадь круга, ограниченного этой окружностью.
Значение числа \(\mathbf<\pi>\) округлить до сотых.
d = 6 cм
Решение:
\(\mathbf<4><\cdot>3,14<\cdot>6^2 = \frac <3,14<\cdot>36> <4>> = 3,14<\cdot>9=28,26\) (cм 2 ) площадь круга
Ответ: \(\mathbf\) (см 2 )
Задача 4
Вычислите площадь полукруга, если радиус круга равен 5 см.
Значение \(\mathbf<\pi >\) округлить до целых.
r = 5 cм
Решение:
Площадь круга найдем по формуле:
Площадь полукруга будет равна половине площади всего круга.
Следовательно, формула для расчета площади полукруга получится вида:
Подставим в формулу известные значения радиуса круга и постоянной \(\mathbf<\pi>\), получим:
\(\mathbf
Ответ: \(\mathbf
Задача 5
Найдите площадь круга, если известна длина окружности С.
Длина окружности С
Решение:
Длина окружности выражается формулой:
Выразим неизвестный радиус окружности через длину окружности:
Площадь круга определяем по формуле:
Подставим, полученные выражения для радиуса окружности, в формулу площади круга, получим:
Сократим полученную дробь:
У меня есть дополнительная информация к этой части урока!
Кроме вычислительных задач, существуют задачи на построение окружности и круга.
Окружность и круг можно начертить с помощью чертежного инструмента, который называется циркуль.
В переводе с латинского языка circulus означает «окружность», «круг».
Циркуль использовали еще с древности, много тысяч лет назад, об этом свидетельствуют найденные на раскопках находки, изображения.
Циркуль представляет собой две одинаковые по длине «ножки». На конце одной из них игла, а на второй- грифель.
Есть циркуль, у которого вместо «ножки» с грифелем помещается карандаш.
Рассмотрим, как построить окружность (круг) на бумаге с помощью циркуля и линейки.
Если задан радиус окружности (круга), то в нулевую отметку на линейке ставим иголку циркуля, другая «ножка» циркуля с грифелем в точку на линейке, равной по значению заданному радиусу.
Не отрывая грифеля второй «ножки» циркуля от бумаги проводим окружность с заданным радиусом.
Если в задаче задан диаметр, то, прежде чем совершать замер по линейке, необходимо диаметр разделить пополам.
Таким образом, устанавливаем раствор циркуля по линейке на расстояние d:2 = r и чертим окружность по выше изложенной схеме.
Данный способ построения окружности (круга) может быть применен и на бумаге, если под рукой не оказалось циркуля.
В качестве колышка берется кнопка, к ней привязывается нить определенной длинны (длина нити равна значению заданного радиуса), ко второму концу привязывается карандаш
Пройти тест и получить оценку можно после входа или регистрации