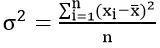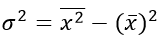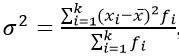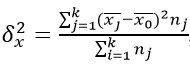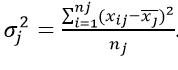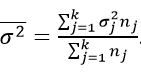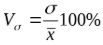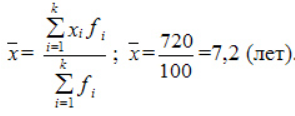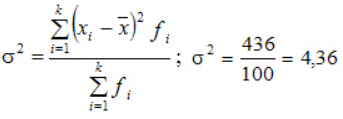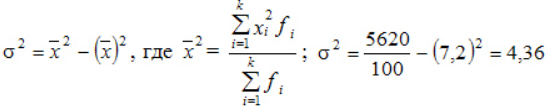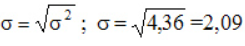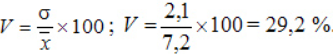что такое дисперсия в статистике простыми словами

Дисперсия и ковариация: что это такое и в чем разница?

Здравствуйте, уважаемые читатели проекта Тюлягин! Сегодня речь пойдет о дисперсии и ковариации, двух на первый взгляд сложных понятий. Однако при более близком рассмотрении вы поймете что в них нет ничего сложного. Эти два термина чаще всего можно встретить в математике и статистике, однако они также используются в финансах и инвестициях. Об этом и поговорим далее в статье.

Содержание статьи:

Что такое дисперсия и ковариация

Дисперсия и ковариация — математические термины, часто используемые в статистике и теории вероятностей. Дисперсия это разброс набора данных вокруг его среднего значения, в то время как ковариация это мера направленного отношения между двумя случайными величинами.

В дополнение к их общему использованию в статистике, оба этих термина имеют также определенные значения для инвесторов, относящиеся к измерениям, проводимым на фондовом рынке, и распределению активов, оба из которых указаны ниже.

Дисперсия простыми словами

Дисперсия используется в статистике для описания разброса между набором данных от его среднего значения. Она рассчитывается путем нахождения взвешенного по вероятности среднего квадрата отклонений от ожидаемого значения. Таким образом, чем больше дисперсия, тем больше расстояние между числами в наборе и средним значением. И наоборот, меньшая дисперсия означает, что числа в наборе ближе к среднему.

Наряду со статистическим определением термин дисперсия также может использоваться в финансовом контексте. Многие биржевые эксперты и финансовые консультанты используют дисперсию акции для измерения ее волатильности. Возможность выразить, насколько далеко стоимость данной акции может отклониться от среднего значения, в одном числе — очень полезный индикатор того, насколько велик риск, с которым связана конкретная акция. Акция с более высокой дисперсией обычно сопряжена с большим риском и потенциалом для более высокой или более низкой доходности, в то время как акция с меньшей дисперсией может быть менее рискованной, что означает, что она будет иметь среднюю доходность.

Ковариация простыми словами

Ковариация — это мера того, как две случайные величины изменятся при сравнении друг с другом. Однако в финансовом или инвестиционном контексте термин ковариация описывает доходность двух разных инвестиций за период времени по сравнению с разными переменными. Эти активы обычно представляют собой рыночные ценные бумаги в портфеле инвестора, например акции.

Положительная ковариация означает, что доходность обоих инвестиций имеет тенденцию одновременно увеличиваться или уменьшаться в стоимости. С другой стороны, обратная или отрицательная ковариация означает, что доходности будут отдаляться друг от друга. Так, когда один актив поднимается, другой актив падает.

Ковариация может измерять движения двух переменных, но не указывает на степень, в которой эти две переменные изменяются по отношению друг к другу.
Ковариацию также можно использовать как инструмент для диверсификации портфеля инвестора. Для этого управляющий инвестиционным портфелем должен искать инвестиции, которые имеют отрицательную ковариацию друг с другом. Это означает, что когда доходность одного актива падает, доходность другого (связанного) актива повышается. Таким образом, покупка акций с отрицательной ковариацией — отличный способ минимизировать риск портфеля. Можно ожидать, что экстремальные пики и спады динамики акций уравновесят друг друга, что приведет к более стабильной норме доходности на протяжении многих лет.

Резюме

А на этом сегодня все про дисперсию и ковариацию, как видите это не так и сложно. Надеюсь статья была для вас полезной и интересной. Делитесь статьей в социальных сетях и мессенджерах и добавляйте сайт в закладки. Успехов и до новых встреч на страницах проекта Тюлягин!

Источник

Что такое дисперсия в статистике

Статистика, в частности, оперирует рядами данных, характеризующих какой-либо признак, явление. Интересует их изменение.

Вариация представляет собой отличие величин одинакового показателя у разных предметов. Ее изучение позволит понять причины отклонений от нормы, анализировать их и в какой-то мере прогнозировать. Также станет возможным выявить факторы, влияющие на значения, отсеяв случайные.

Характеристики равномерного распределения представлены на картинке:

При значительном объеме статистики, средняя величина очевидно близка к нормальной. Об этом говорят и законы распределения. Отклонения от нее будут являться объективной характеристикой.

Только вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять лишь модули – для математика не корректно. Напрашивается возвести в четную степень, а именно – во вторую.

Решение оказалось не только удобным. Оно открыло бо́льшие возможности в изучении отклонений. А важны именно они, поскольку сама по себе средняя мало что дает.

В качестве одного из важных показателей вариации, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-либо событий от средней величины.

Никакого наглядного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.

Виды дисперсии дискретной случайной величины

Для анализа данных цифр в таком виде недостаточно. Гораздо больше можно выжать из последовательности, если разбить ее на группы по определенному признаку.

Общая дисперсия

Как можно заметить, вычисленная по приведенному выше определению величина характеризует отклонения в целом. Без учета определяющих вариацию факторов. Вернее, с учетом всех, включая совершенно случайные. Поэтому и называется «общей» и рассчитывается по формулам, указанным ниже.

Простая дисперсия, без разделения на группы:

Или в несколько преобразованном виде:

Взвешенная дисперсия, для вариационного ряда:

где x_i – значение из ряда;

f_i – частота, количество повторений;

n – число вариантов.

Черта сверху указывает на среднюю величину.

Межгрупповая дисперсия

Характеризует систематическое отклонение, возникающее из-за фактора, по которому производилось выделение признаков в группы. Поэтому также называется «факторной».

Как найти данную дисперсию? По формуле:

где k – количество групп;

n_j – элементов в группе с индексом j.

Внутригрупповая дисперсия

Возникает по хаотичной причине, не связанной с причиной сделанной выборки. Неучтенный фактор. Еще обозначается как «остаточная».

Например, рассматривается количество выпущенных деталей за месяц каждым фрезеровщиком цеха.

В качестве критерия отбора в группу выбираем возраст оборудования. Он-то и не будет влиять на производительность внутри подборки: там станки у всех практически одинаковые.

Если вычислить среднюю величину от всех групповых,

то получим характеристику случайного разброса. Иными словами, составляющую вариации, зависящую от чего угодно, кроме фактора отбора.

Взаимосвязь

В соответствии с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это логично, поскольку учитывает и случайное изменение в группе, и систематическое в факторной.

Свойства дисперсии

Если последовательность состоит из одинаковых чисел, то D[X] будет нулевой.

Уменьшение всех значений на постоянную величину на дисперсию не влияет. Иначе говоря, рассчитать σ 2 можно по отклонениям от фиксированного числа.

Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, например, иметь в виду значения в метрах, а результат вычислить в футах. Достаточно учесть один раз то, на что следует умножить.

Показатели вариаций

Кроме размаха (разницы максимального и минимального значений), среднего линейного и дисперсии, изменения описываются коэффициентом вариации:

Оценить масштаб разброса проще по относительной величине. Тем более, что измеряются в одних единицах.

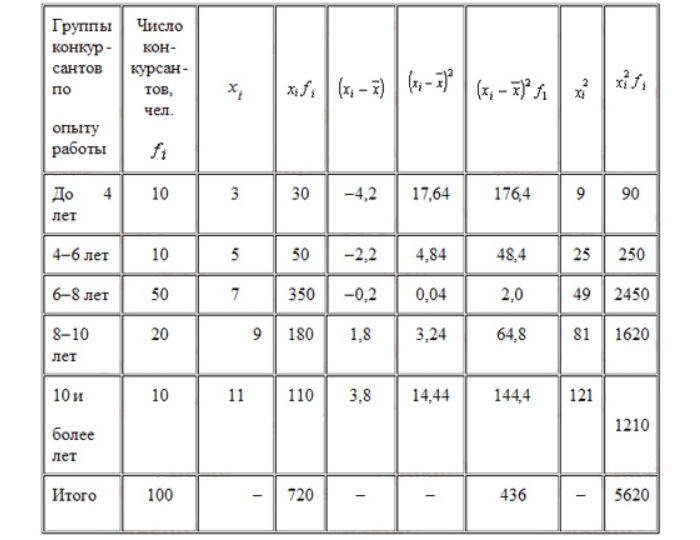
Пример расчета дисперсии

Компания объявила конкурсный отбор для приема сотрудников. В качестве критерия принят стаж работы по специальности. Приведем исходные данные и расчеты.

По альтернативной формуле:

Заключение

Статистика оперирует значительными объемами данных. Вариация, как одно из основных понятий – не исключение. И дисперсия в качестве основной характеристики.

Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.

Источник

7 базовых статистических понятий, необходимых дата-сайентисту

Даже если вы хорошо программируете, но слабо ориентируетесь в статистике, вероятность выжить в Data Science очень низка.

У статистики есть несколько различных определений. Одно из самых простых и точных — это «наука о сборе и классификации цифровых данных». А если добавить к нему немного о программировании и машинном обучении, то получится неплохое описание основ Data Science.

В самом деле, в Data Science трудно найти область, где нет статистики в том или ином виде. Она нужна для:

Мы выбрали семь базовых концепций, без которых в Data Science точно не обойтись. К счастью, они не слишком сложны.

С некоторых пор утверждает, что он data scientist. В предыдущих сезонах выдавал себя за математика, звукорежиссёра, радиоведущего, переводчика, писателя. Кандидат наук, но не точных. Бесстрашно пишет о Data Science и программировании на Python.

1. Меры описательной статистики

Ключевые показатели, применяемые в описательной статистике (их ещё называют мерами или, если точнее, мерами центральной тенденции), — это:

Посмотрите это небольшое видео о среднем, медиане и моде на сайте Академии Хана — образовательного ресурса, который славится доходчивыми объяснениями. Там всё просто, на понятном русском языке.

Кроме трёх перечисленных, есть и другие статистические показатели — например, меры рассеяния. Главная из них — дисперсия, о ней ниже. Все они нужны, чтобы понять, какие перед нами данные и о чём именно они рассказывают.

2. Распределение

Внешняя форма данных, выраженная в мерах описательной статистики, даёт нам информацию об их характере. Это как в жизни: по фигуре, походке и одежде человека обычно можно догадаться о его поле, возрасте и даже профессии. В случае числовых данных мы догадываемся о распределении.

Термин пришёл из теории вероятностей, которая рассматривает любое событие в мире как имеющее ту или иную вероятность. Однородные события хоть и происходят с разной вероятностью, но подчиняются распределению, которое «раздаёт» им эти вероятности.

В Data Science распределение понимается обобщённо: это закон соответствия одной величины другой. Оно подсказывает нам, какой именно процесс может скрываться за данными, и то, насколько эти данные полны. Чуть подробнее об этом в нашей статье про математику для джунов.

Возможно, вы уже слышали про колокол нормального распределения, или гауссиану: она описывает процессы, где результат является суммой многих случайных величин, каждая из которых слабо зависит от другой и вносит сравнительно небольшой вклад.

Величина ошибок измерения в физике, длина когтей, зубов и шерсти в биологии, объёмы речных стоков в гидрологии — все эти показатели имеют нормальное распределение. Это, пожалуй, самое распространённое в природе и не только в природе распределение, поэтому оно и названо нормальным.

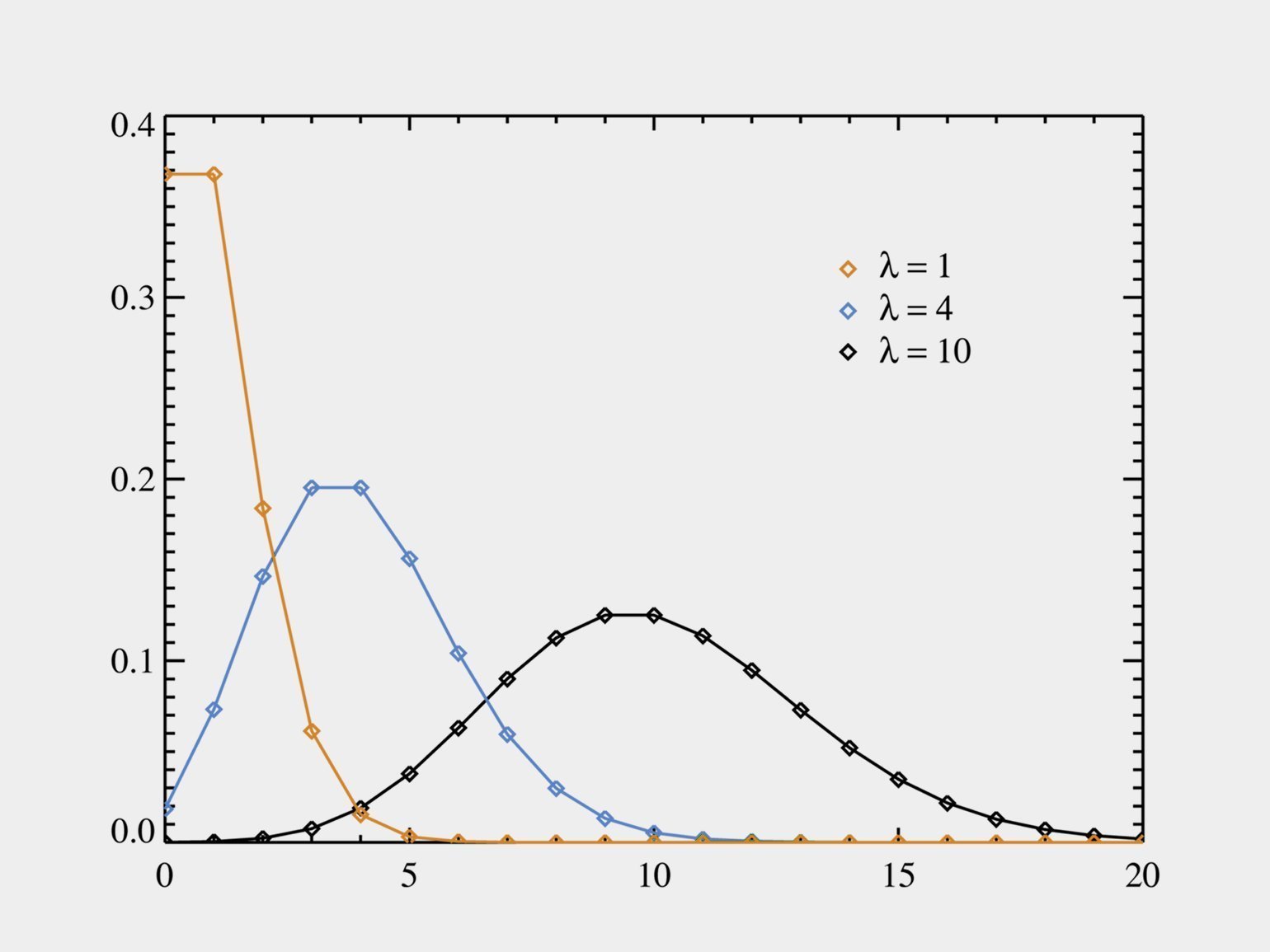
Распределение Пуассона тоже часто встречается в работе дата-сайентистов и аналитиков: это число событий за какой-то промежуток времени — при условии, что события независимы друг от друга и имеют некоторый порог интенсивности.

Это и число посетителей в торговом центре, и количество голов, забитых футбольной командой, и скорость роста колонии бактерий.

Существуют и другие распределения, в том числе довольно экзотические: Вигнера, Вейбулла, Коши. Они встречаются намного реже или преимущественно в каких-то специальных областях вроде квантовой физики. Тем не менее дата-сайентисту нужно знать графики, параметры и названия основных распределений, благо их не так много.

3. Семплирование

Предположим, вам требуется решить важную задачу: выяснить среднюю ширину морды домашних котов нашей страны. Прямой способ, то есть измерение всех домашних питомцев, невозможен по ряду объективных причин. Придётся ограничиться выборкой — взять какое-то число животных, измерить морды именно им и сделать выводы по итогам только этих исследований.

Но тут сразу же возникают вопросы:

Семплирование — это группа статистических методов и приёмов, отвечающих на эти вопросы. С помощью семплирования мы формируем нашу выборку так, чтобы она наилучшим образом отражала свойства генеральной совокупности — то есть свойства всех котов страны.

Иными словами, вы не можете измерить N первых попавшихся котов и обобщить результат для остальных. Выборка должна хорошо «сидеть» во всей популяции кошек, чтобы можно было делать обоснованные выводы. Такую выборку называют релевантной.

Кстати, статистика и котики — близнецы-братья. После выхода одноимённой книги Владимира Савельева мы говорим «статистика», а подразумеваем «котики», и наоборот. И смело рекомендуем эту книгу всем, кто дочитал до этого места.

В Data Science методы семплирования применяются при разработке, подготовке и оценке датасетов, чтобы они одновременно и были упорядоченными, и соответствовали реальности.

4. Смещение

Прочитайте нашу статью о создании простой модели машинного обучения. Она предсказывает город, в который вероятнее всего поедет турист, на основании его возраста, пола, места жительства, дохода и транспортных предпочтений. Такая рекомендательная система на минималках.

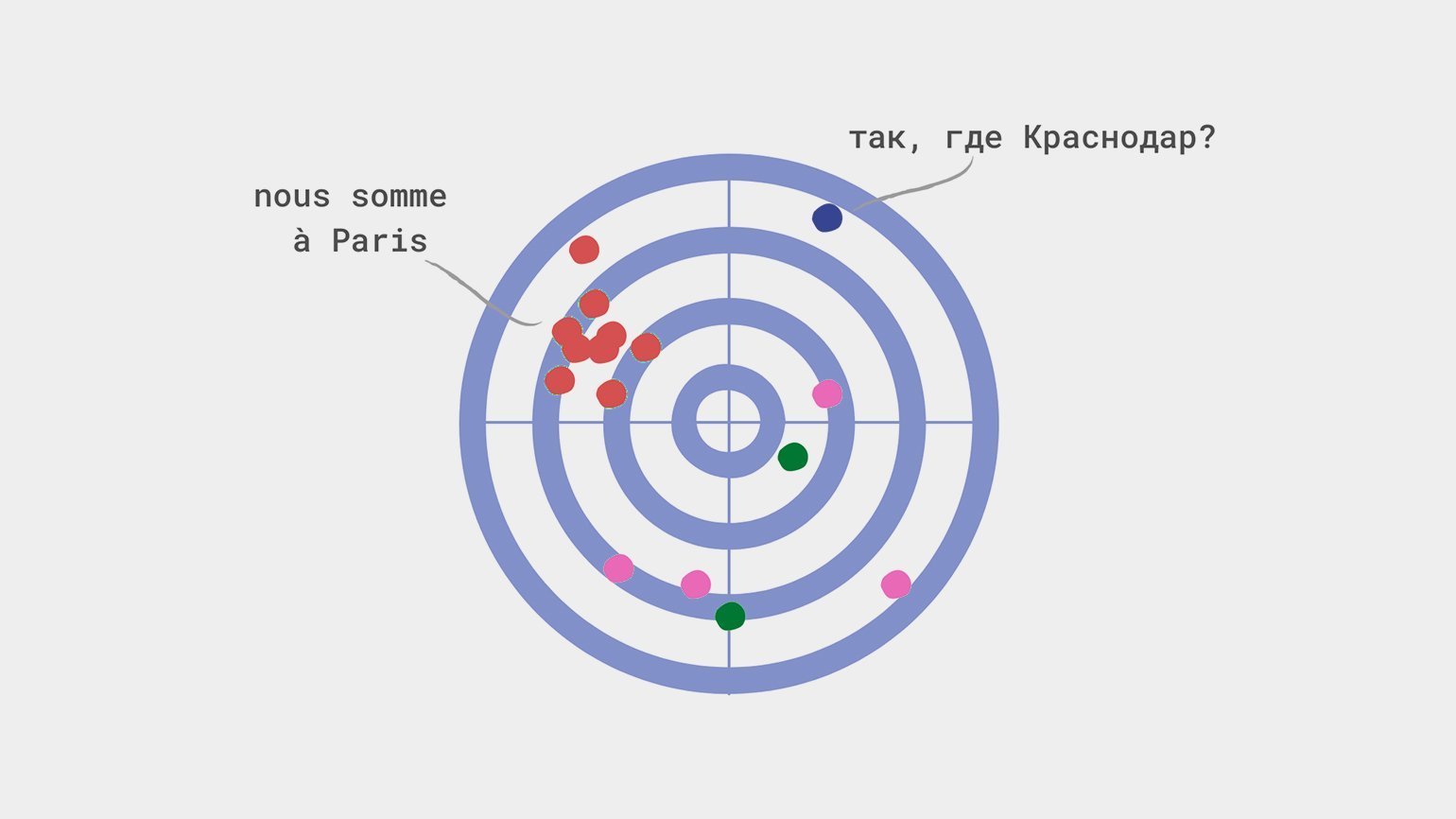
Смещение происходит, когда модель недооценивает или переоценивает какой-либо параметр. Представим, что модель из статьи выше отправляет всех краснодарцев в Париж — независимо от их дохода, предпочтений и других параметров. В этом случае мы скажем, что модель переоценивает значение параметра «Город проживания».

Чаще всего причиной смещения являются:

Когда мы неверно собираем данные, говорят о систематической ошибке отбора. Например, в прошлом веке многие считали, что во Вселенной больше голубых галактик, — впечатление возникало потому, что плёнка была более чувствительна к голубой части спектра.

Другая ошибка — ошибка меткого стрелка — происходит, когда мы вольно или невольно отбираем в выборку только схожие между собой данные, то есть фактически рисуем мишень вокруг места, куда попадём.

Причин, вызывающих смещение, так много, что Марк Твен заметил: «Существует три вида лжи: ложь, наглая ложь и статистика». Например:

Эти и другие ошибки смещения трудно выявить статистическими методами, поэтому нужно стараться избежать их до того, как вы начнёте сбор данных.

Если пить «Боржоми» уже поздно (датасет уже сформирован), обязательно спросите себя: «Не смещены ли мои данные?» — а они наверняка смещены, «Куда и почему они смещены?» и «Можно ли с этим жить?»

5. Дисперсия

Дисперсия — это величина, показывающая, как именно и насколько сильно разбросаны значения — например, предсказания модели машинного обучения или доход за рассматриваемый период. За точку, относительно которой эти значения разбросаны, берут истинное значение, целевую переменную или математическое ожидание, которое вычисляется теоретически и заранее.

Часто в качестве матожидания выступает обычное среднее арифметическое. Например, математическое ожидание количества очков при броске игрального кубика равно среднему арифметическому очков на всех гранях:

(1 + 2 + 3 + 4 + 5 + 6) / 6 = 21/6 = 3,5

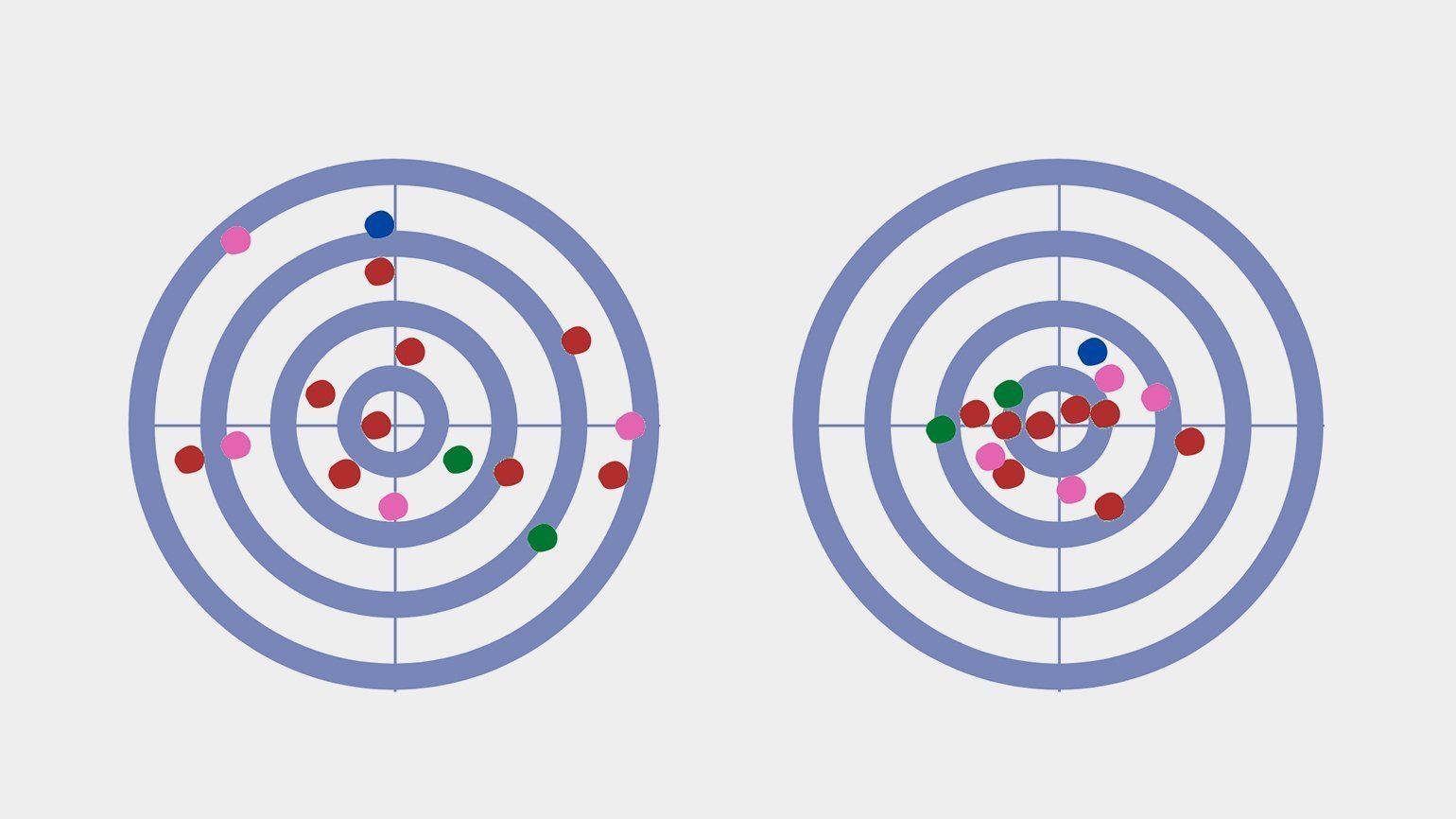
Представьте себе тир, стрелка и мишень. Снайпер стреляет в стандартный круг, где попадание в центр даёт 10 баллов, в зависимости от удаления от центра количество баллов снижается, а крайние области дают всего 1 балл. Каждый выстрел стрелка — это случайное целое значение от 1 до 10.

Изрешечённая пулями мишень — отличная иллюстрация распределения. Дисперсия здесь — величина, обратная кучности попаданий: хорошая кучность означает низкую дисперсию, и наоборот.

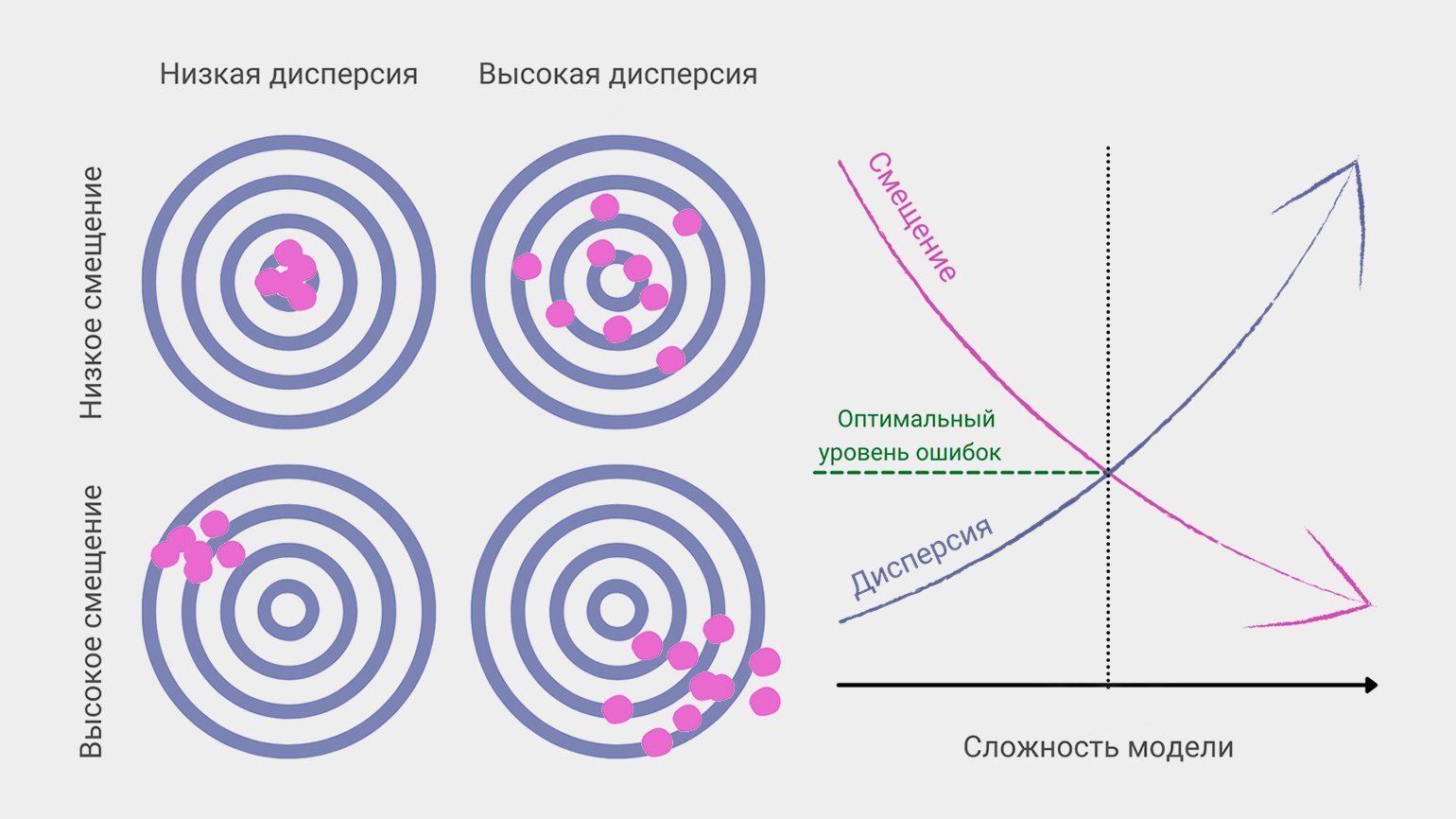
6. Дилемма (компромисс) смещения и дисперсии

Смещение и дисперсия вместе составляют итоговую ошибку предсказания модели машинного обучения. В идеальном мире и смещение маленькое, и дисперсия низкая. На практике это связано в дилемму: уменьшение одной из величин неизбежно приводит к росту другой.

Если не вдаваться в детали, обучение модели — это построение функции, график которой лучше всего ложится на точки из тренировочного набора данных.

Модель может нарисовать нам довольно сложную и заковыристую функцию, график, который хорошо охватывает все точки в тренировочных данных. Но если наложить этот график на новые точки (то есть дать функции новые данные), она сработает хуже — так и получается смещение.

С другой стороны, обучение на разных тренировочных наборах или даже разных датасетах с большой вероятностью даст разброс в предсказаниях, то есть высокую дисперсию.

Более сложные модели дают низкое смещение, но чувствительны к шуму и колебаниям в новых данных, поэтому их предсказания разбросаны. Если при обучении наш снайпер будет учитывать незначимые факторы (вроде цвета мишени или направления магнитного поля Земли), то в другом тире, с другой винтовкой или в другую погоду точность его стрельбы упадёт.

Простые модели, напротив, упускают важные параметры и «бьют кучно, но мимо». Как другой снайпер, не приученный обращать внимание на ветер и расстояние до мишени.

В процессе настройки модели машинного обучения дата-сайентист всегда ищет компромисс между смещением и дисперсией, чтобы уменьшить общую ошибку предсказания.

Кстати, эта дилемма встречается не только в статистике и машинном обучении, но и в обучении людей. В исследовании 2009 года утверждается, что люди используют эвристику «высокое смещение + низкая дисперсия»: мы заблуждаемся, зато очень уверенно.

Учтите это, если захотите сделать свой ИИ более похожим на человека.

7. Корреляция

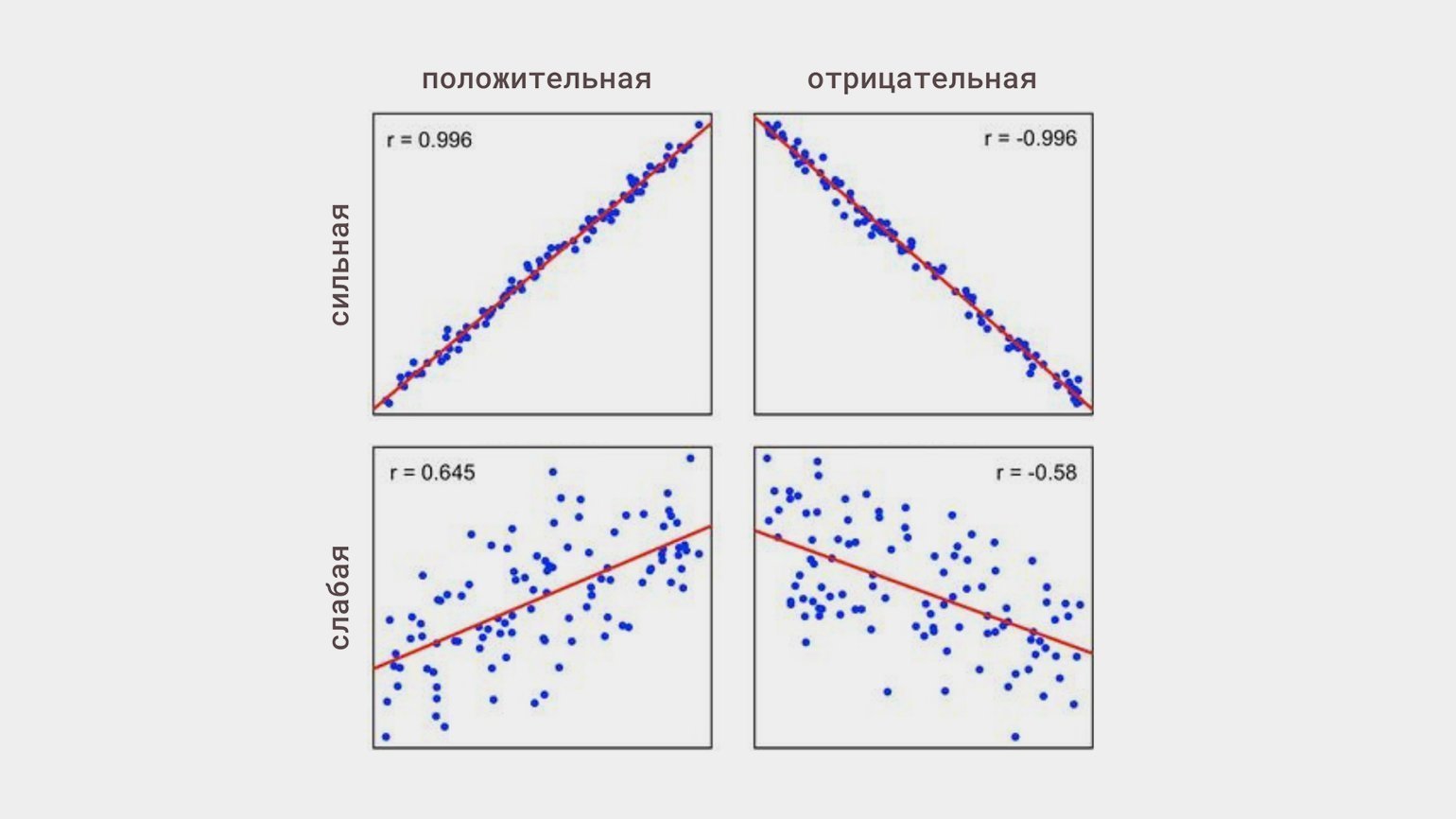
Когда изменения одной величины сопутствуют изменениям другой, говорят о корреляции. Главное, что необходимо о ней знать: корреляция не означает причинно-следственную связь.

Линейная корреляция — это когда изменения одной величины пропорциональны изменениям другой. Она может быть:

Статистическую связь между переменными исследуют с помощью корреляционного анализа. Его основная задача — оценить тесноту связи (это термин) между переменными, чтобы понять, какие переменные учитывать в модели, а какие нет.

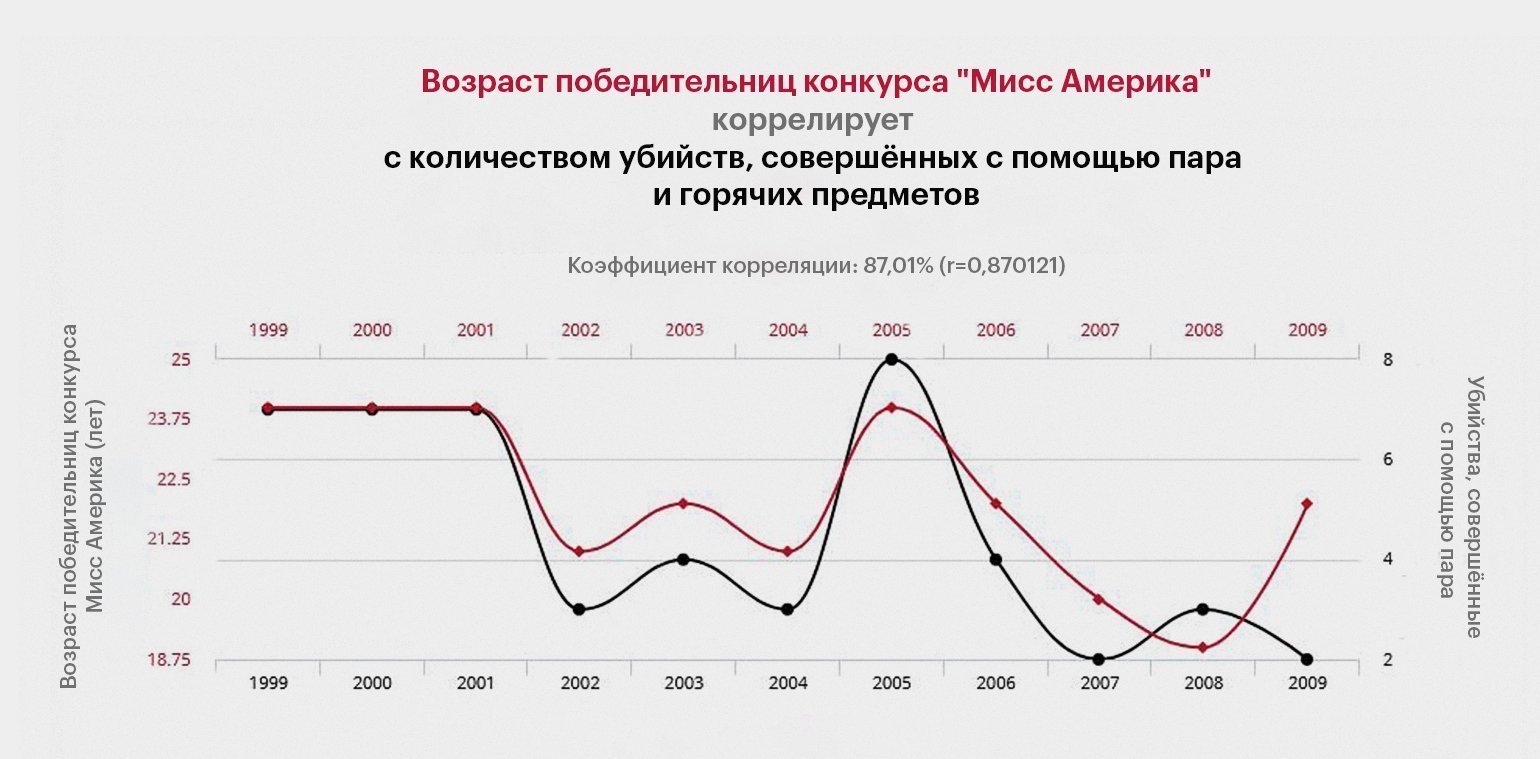
И ещё раз, потому что действительно важно: корреляция ни в коем случае не означает причинно-следственную связь. Если два показателя скоррелированы, то далеко не факт, что они хоть как-то связаны.

Кстати, проект Spurious Correlations («Ложные корреляции») публикует графики корреляций между совершенно неожиданными статистическими показателями — например, количеством людей, утонувших в домашних бассейнах, и числом фильмов с участием Николаса Кейджа.

Имеет смысл время от времени заходить по этой ссылке с целью профилактики СПГС — синдрома поиска глубинной связи.

Заключение

Data Science — не просто комбинирование модных моделей в Jupyter-ноутбуке. Профессионалы в этой области глубоко понимают природу данных и то, как они могут помочь в принятии конкретных бизнес-решений.

Всё это изучалось в статистике задолго до того, как первый дата-сайентист набрал свой первый import pandas as pd. Статистика — фундамент всей современной науки о данных, включая машинное обучение, глубокие нейросети и даже искусственный интеллект.

В нашем курсе «Профессия Data Scientist» статистике уделено самое пристальное внимание. Вы не ударите в грязь лицом ни на тусовке статистиков, ни на настоящем DS-собеседовании. Приходите!

Источник