что такое дискретная величина в информатике
Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.
Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.
Дискретность – это …
Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.
В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.
Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:
Дискретность можно толковать следующим образом:
Далее проанализируем особенности применения термина в различных областях.
Дискретная математика
Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.
ДМ условно подразделяется на пять направлений:
Дискретная величина
Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.
Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.
Дискретность в информатике
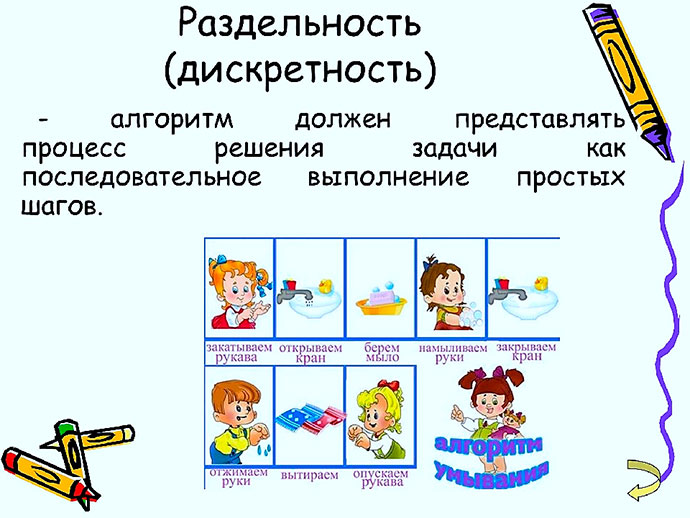
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).
Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.
Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):
Дискретная видеокарта
Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.
Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.
Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.
Дискретность в биологии
Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.
Автор статьи: Елена Копейкина
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Благодарю за дискретное изложение материала
Дискретность информации. Дискретизация
Вы будете перенаправлены на Автор24
Формы представления информации
Информация представляет собой понятие довольно емкое, вмещающее в себя весь окружающий нас мир (это вещи, явления, история, литература, искусство и многое другое). Всю информацию можно представить в двух формах:
Познакомимся с ними более детально.
Физические величины, а точнее их значения, характеризуют объекты и явления. Например, человека могут характеризовать такие физические величины, как масса тела, рост, температура тела, давление и т.д. В качестве явления, например, природы можно рассмотреть ураган, который будет характеризоваться такими физическими величинами, как скорость ветра, температура воздуха, количество выпавших осадков.
Некоторые физические величины по своей природе таковы, что могут принимать любые значения в определенном диапазоне. Эти значения могут находиться достаточно близко друг от друга, но тем не менее они различаются, а количество же значений, которое может принимать величина, бесконечно велико.
Подобные величины называют непрерывными, соответственно информацию, которая выражается с помощью этих величин, также называют непрерывной.
Помимо непрерывных величин существуют и другие, например, количество спортсменов на стадионе, количество атомов в молекуле и т.д. Подобные величины могут принимать только целые значения и не могут иметь дробных значений.
Величины, которые могут принимать не все возможные значения, а только вполне конкретные, называют дискретными. Дискретные величины характеризуются тем, что все их значения можно пронумеровать целыми числами.
Примерами дискретных величин являются:
Таким образом, различие между двумя формами информации строится на принципиальном различии природы величин. В то же время непрерывная и дискретная информация могут использоваться одновременно для более полного представления сведений об объектах и явлениях.
Готовые работы на аналогичную тему
Попробуем разобраться, что может объединять непрерывные и дискретные величины.
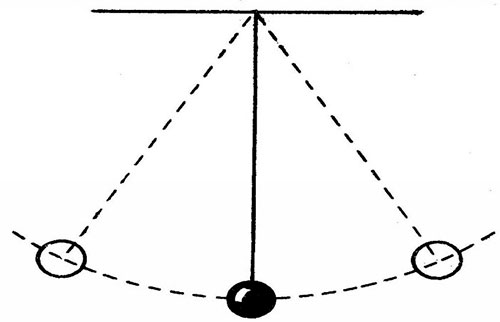
Рассмотрим простой пример и опишем наши рассуждения, в качестве примера возьмем пружинные весы. Масса тела, которую можно измерить с их помощью, представляет собой непрерывную величину. В данном случае информация о массе содержится в длине отрезка, на которую переместился указатель весов под непосредственным действием массы тела. Длина отрезка также представляет собой непрерывную величину.
Возникает вопрос, а можно ли по дискретному представлению восстановить непрерывную величину? Да, это действительно в определенной степени возможно, однако сделать это достаточно сложно, в результате восстанавливаемый образ может отличаться от подлинника.
Формы представления дискретной информации
В качестве имен можно использовать натуральные числа. Подобным образом нумеруются страницы книг, дома, деления на шкалах измерительных приборов. С помощью чисел можно пронумеровать все. Именно такая цифровая форма представления информации используется в ЭВМ.
В повседневной жизни цифровая форма представления информации не совсем практична. Традиционно информацию об объектах и явлениях окружающего мира мы представляем в форме слов и их последовательностей.
Слово является основным элементом в данной форме представления информации, с помощью него обозначаются имена объектов, действий, свойств и т.п.
Слова строятся из букв конкретного алфавита (например, русского). Помимо букв могут использоваться специальные символы: знаки препинания, математические символы и знаки и т.п. Разнообразные символы, которые мы используем, образуют алфавиты, на их основе, в свою очередь, можно построить различные объекты:
Во всех этих объектах заключена информация:
Эта информация по своей природе дискретна и может быть представлена в виде последовательности символов. Такая информация представляет собой особый вид дискретной информации, который называют символьным.
В настоящее время существует множество разных систем письменности, с помощью которых одна и та же информация может быть представлена на основе самых разных наборов символов и самых разных правил использования символов при построении слов, фраз, текстов.
Таким образом, разные алфавиты обладают одинаковой «изобразительной возможностью», т.е. с помощью одного алфавита можно изобразить информацию, которую удалось изобразить с помощью другого алфавита. Можно, к примеру, использовать алфавит, состоящий из 10 цифр, и с его помощью записать текст любой книги. При этом исключена потеря информации. Кроме того, можно использовать алфавит, состоящий только из двух символов (0 и 1). И его «изобразительная возможность» будет аналогичной.
Следовательно, символьная информация может быть представлена с помощью различных алфавитов без искажения содержания и смысла информации.
Помимо приведенных выше существуют и другие формы представления дискретной информации. К ним можно отнести чертежи, схемы, содержащие графическую информацию.
Дискретизация информации
Обмен информацией в системах обработки информации происходит при помощи сигналов. В качестве носителей сигналов могут выступать любые физические величины, которые представляют собой функции времени или определенное пространственное распределение сигналов. Параметры передаваемых временных функций (частоты, амплитуды, фазы, длительности импульсов или пространственного распределения последовательных импульсов, точек на изображении, сочетаний цветов на экране и др.) являются информационными параметрами сигнала.
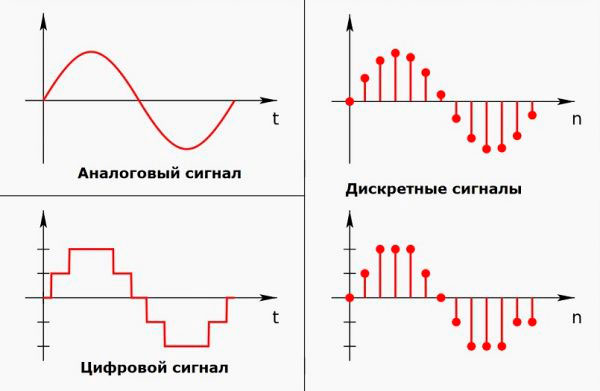
Непрерывные сигналы в системе координат (уровень и время) описывают с помощью непрерывных функций. Преобразование аналогового сигнала в дискретный связано с его дискретизацией по уровню и во времени.
Дискретные сигналы довольно таки просто хранить и обрабатывать, поскольку они мало подвергаются искажениям под влиянием помех, причем последние легко обнаружить. В связи с этим дискретные сигналы наиболее широко применяются, чем непрерывные.
Преобразование непрерывного информационного множества аналоговых сигналов в дискретное множество называется дискретизацией или квантованием по уровню.
Квантование по уровню широко применяется в цифровых автоматах, поскольку производится отображение всевозможных значений величины X на дискретную область, состоящую из величин X, уровней квантования.
При дискретизации по времени (квантование по времени) непрерывная по времени функция преобразовывается в функцию дискретного аргумента времени. Дискретизация непрерывных сигналов построена на принципе представления их в виде взвешенных сумм. Органы чувств человека не совершенны, и в связи с этим окружающий нас мир мы воспринимаем дискретно. Использование различных приборов, которые увеличивают чувствительность или разрешающую способность, принципиально ничего не дает, меняет лишь шаг дискретизации.
Что такое дискретная величина в информатике
Код ОГЭ: 1.1.3 Дискретная форма представления информации. Единицы измерения количества информации
Информация может быть представлена в аналоговой или дискретной форме. Величина в аналоговой форме может принимать бесконечное множество значений. Примерами аналогового представления информации могут служить звук скрипки, картина художника, показатели температуры воздуха, уровня воды в реке.
Величина в дискретной форме может принимать только конечное множество значений. Примеры дискретного представления информации: цифровые показания часов или спидометра, текст в книге, изображение на экране монитора.
Величину в аналоговой форме представления информации можно преобразовать в величину в дискретной форме. Этот процесс называется дискретизацией.
Способ представления информации с помощью кода из двух знаков оказался наиболее значимым для развития техники. Двоичные числа удобно хранить, обрабатывать и передавать с помощью электронных устройств. Основным носителем информации в них являются элементы, которые могут находиться в одном из двух состояний: включено/выключено, высокий/низкий уровень напряжения или тока, наличие/отсутствие намагниченности материалов. Условно одно состояние обозначают через 1, а другое через 0. Каждый такой элемент способен хранить один двоичный разряд, или бит информации.
Любое информационное сообщение представляется последовательностью нулей и единиц (цифрового кода). Этот метод представления информации называется двоичным кодированием. Таким образом, двоичный код является универсальным средством кодирования информации. Благодаря двоичному кодированию все действия по обработке сообщений компьютером сводятся к совокупности простых действий над 0 и 1.
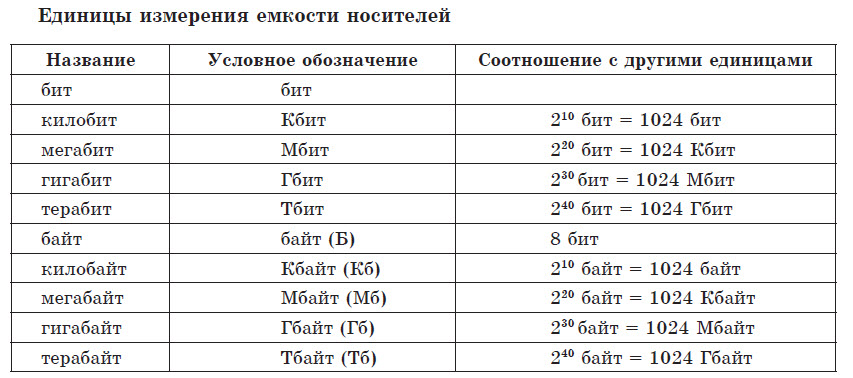
Единицы измерения количества информации
Основной единицей хранения и обработки цифровой информации принят байт.
Соответственно, с помощью одного байта можно получить 256 (= 2 8 ) двоичных значений (от 00000000 до 11111111). В современных персональных компьютерах байт является наименьшей совокупностью битов, которую компьютер обрабатывает одномоментно.
На практике применяют более емкие, чем байт, единицы измерения объема сообщений и емкости носителей — килобайты, мегабайты, гигабайты, терабайты. Множителем при переходе к более емкой единице измерения выступает число 1024 (= 2 10 ).
Системы счисления
Система счисления — совокупность обозначений, приемов и правил для записи чисел цифровыми знаками. В зависимости от способов изображения чисел цифрами системы счисления делятся на непозиционные и позиционные.
Непозиционные системы счисления — такие, в которых количественное значение каждой цифры не зависит от занимаемой ею позиции в изображении числа.
Примером может служить египетская система счисления — в ней иероглифы (цифры), составляющие число, можно записывать сверху вниз, справа налево или вперемежку. Значение числа равно сумме значений цифр в его записи.
Переходной от непозиционных систем к позиционным служит римская система счисления. В ней позиция некоторых цифр уже меняет значение числа: например, в числе IX единицу нужно отнять от десяти, а в числе XI единицу нужно прибавить к десяти. Однако количественное значение самих цифр Х и I от их позиции не зависит.
В римской системе цифры записываются слева направо в порядке убывания, и тогда их значения складываются. Если слева записана меньшая цифра, а справа — большая, то их значения вычитаются. Нежелательно записывать более трех одинаковых цифр подряд.
Например, для представления числа 348 в римской системе счисления надо выписать сначала число сотен, затем десятков и единиц: 300 — ССС, 40 — ХL, 8 — VIII. Затем соединить эти записи: CCCXLVIII. Аналогично для числа 1977: 1 тысяча — М, 900 — СМ, 70 — LXХ, 7 — VII. Результат: MCMLXXVII.
В непозиционных системах очень трудно производить многие действия над числами, особенно умножение и деление, слишком громоздка запись для больших чисел. Поэтому широкое распространение получили позиционные системы счисления.
Позиционные системы счисления — такие, в которых количественное значение каждой цифры зависит от ее позиции в числе.
Количество знаков (цифр), используемых для изображения числа, называется основанием системы счисления (или мощностью алфавита). Систему с основанием 10 называют десятичной, с основанием 2 — двоичной, с основанием 16 — шестнадцатеричной, в общем случае: с основанием k — k-ичной.
Примером позиционной системы счисления является используемая нами арабская десятичная система счисления. Иногда ее называют индо-арабской, поскольку она была придумана в Индии, а стала известна в Европе из арабских трактатов. Алфавит этой системы составляют 10 цифр — от 0 до 9. Каждая цифра в числе при перемещении справа налево в следующий разряд увеличивает свое значение в 10 раз. Чтобы определить значение числа, надо сложить произведения каждой его цифры на 10 в степени, равной разряду этого числа.
348 = 3 • 10 2 + 4 • 10 1 + 8 • 10 0
–348,17 = –(3 • 10 2 + 4 • 10 1 + 8 • 10 0 + 1 • 10 –1 + 7 • 10 –2 )
Системы счисления могут иметь различные основания. Чтобы различать, в какой системе счисления записано число, принято указывать ее основание в виде нижнего индекса справа от числа. Сам индекс всегда представляется в десятичной системе. Для самой десятичной системы индекс указывают только тогда, когда используется какая–либо другая система:
316 — число в десятичной системе счисления,
3168 — число в восьмеричной системе счисления.
Свойства записи чисел в позиционной системе счисления:
Если основание системы k больше 10, то цифры старше 10 при записи обозначают прописными буквами латинского алфавита: A, B, …, Z. При этом цифре 10 соответствует знак A, цифре 11 — знак B и т. д.
Информация в компьютере представлена в цифровой двоичной форме. В целях экономичного отображения двоичную информацию можно представлять в шестнадцатеричном виде. В программировании часто используется восьмеричная запись чисел.
В общем виде число в позиционной системе счисления может быть представлено как последовательность символов алфавита (цифр), обозначенных через а1, а2, а3 и т. д. Для числа А с количеством целых разрядов n и количеством дробных разрядов m запись имеет вид:
Такая запись называется свернутой записью числа. Эту форму записи мы используем в повседневной жизни, поэтому ее называют также естественной.
Представление числа в виде многочлена называют развернутой записью числа:
Развернутая запись числа задает правило для вычисления числа по его цифрам в k–ичной системе счисления. Для уменьшения количества вычислений пользуются схемой Горнера, которая получается путем поочередного выноса основания системы k за скобки:
Конспект урока по информатике «Дискретная форма представления информации».
Дискретность информации и понятие дискретизации: следование от бытовых примеров к информатике
Информация – понятие ёмкое, вмещающее весь мир, что окружает нас. Элементами ее выступают явления, вещи, искусство, история и пр.
Формы предоставления информации
Представляется информация в таких формах:
Явления и объекты обладают характерными физическими величинами. Человека, к примеру, могут характеризовать:
А в природе, в виде примера, можно обозначить циклон. Его характерные величины – количество выпадающих осадков, температура воздуха, скорость ветра и т. д.
То есть для физических величин характерен определённый диапазон. Характеризующие величины могут оказаться почти подобными. Однако они различаются, и количество значений, принимаемых определённой величиной, бесконечно в своём разнообразии.
Эти величины именуются непрерывными, как и та информация, что выражается с помощью подобных величин. Ее также называют непрерывной. Причём непрерывность – основное свойство таких величин. Другими словами, между значениями не может быть разрывов.
Примером может служить значение массы тела. Это величина непрерывная, так как показатель способен колебаться от величины, исходящей с начального значения 0, и до бесконечности.
Но существуют и другие величины, помимо непрерывных, обозначающие количество, к примеру, атомов в молекуле, спортсменов на стадионе и пр. Значения таких показателей – целые числа, а не дробные.
Определение понятия дискретности
Такие целые числа можно пронумеровать. Поэтому, пытаясь глубоко разобраться, что такое дискретная информация, следует учитывать ее прерывистость и цифровое обозначение признаков в виде логического нуля и такой же логической единицы.
Выходит, что две основные формы информации имеют принципиальные различия, заключающиеся в природе каждой величины. Но чтобы зафиксировать более объёмные сведения о явлении или объекте, часто используют эти информации единовременно.
Пример 1. Высота какого-то треугольника – 26, 04 см. Здесь дискретное представление информации заключается в обозначении понятия «треугольник» – конкретной геометрической фигуры. А вот значение 26,04 – это информация непрерывная, она передаёт сведения об одном из показателей этой фигуры.
Пример 2. Берутся пружинные весы. Измеряемая ими масса – величина непрерывная. Информация заключена в длине отрезка, по которому перемещается показатель весов, ведь на этот механизм непрерывно воздействует масса тела.
Некоторые механические ювелирные весы имеют шкалу в диапазоне от 0,1 г (полкарата) до 1000 г. Самоцвет будет обладать одним из конкретных показателей из этого набора значений – к примеру, 8,3. Значит этим однозначным показателем закладывается дискретная форма представления информации о массе.
Удаётся даже по дискретному представлению восстановить непрерывную величину. Но в результате дискретная форма выведенного образа может не совпадать с реальным подлинником.
Что такое дискретность в информатике
Другими словами, дискретность это в информатике возможность решить задачу путём распределения процесса на отдельные последовательные шаги. Каждая сформированная совокупность команд или предписаний выделена. Только исполнив одну команду, удаётся приступить к исполнению последующей.
В какой форме представляется дискретная информация
Есть конечное перечисление разнообразий, помогающих определить явление, объект. Выделяя из возможного конкретный вариант, его обозначают индивидуально – присваивают имя. Как раз конкретное наименование и несёт смысловую нагрузку информации, касающейся явления или объекта. Таким именем может стать натуральное число:
Всё на свете можно пронумеровать, указать числами. Когда требуется представить информацию в ЭВМ, используется именно цифровая форма обозначений.
А в повседневной жизни представлять информацию исключительно цифрами не практично, поэтому используются последовательно произносимые слова:
Слова составляются из букв, используется конкретный алфавит (русский, английский и пр.). Также применяются символы:
Символы образуют своеобразные алфавиты, используя которые, можно создавать различные объекты.
Природа такой информации дискретна, она заключена в последовательных символах. Поэтому данный вид информации именуют символьным.
Уже разработано огромное количество систем письменности, помогающих идентичную информацию передавать с помощью разных символических наборов, а также всевозможных правил применения этих символов, из которых составляются слова, отдельные фразы, целые тексты.
Выходит, что у разных алфавитов имеется одинаковая «изобразительная возможность». Ту информацию, что можно передать с одного алфавита, удаётся передавать и с других. Таким способом, используя в виде алфавита, к примеру, всего 10 цифр, можно составить текст книги без потери информации. В алфавите может даже быть всего два различных символа (0 и 1), при этом «изобразительная возможность» его будет аналогичной.
Кроме приведённых выше примеров, разрабатываются и другие форматы представления дискретной информации:
Дискретизация информации
В системе обработки информации дискретизация представляет собой ее обмен, осуществляемый с помощью сигналов. Их носителями способны выступать определённые физические величины, представленные пространственным распределением сигналов, функциями времени.
Информационными параметрами сигнала выступают показатели передаваемых временных функций:
Различие сигналов
При квантовании (дискретизации) по времени функция, также непрерывная по времени, обретает способность преобразования в функцию дискретного аргумента времени. Построение дискретизации непрерывных сигналов производится по принципу их представления в образе взвешенных сумм.
Человек обладает далеко не совершенными органами чувств, значит он воспринимает окружающий мир дискретно. Даже применение архисложных приборов, способствующих повышению чувствительности или разрешающей способности, принципиально положение изменить не может. При этом шаг дискретизации всё же меняется.