что такое дискретная оценка
дискретная оценка
Смотреть что такое «дискретная оценка» в других словарях:
ГОСТ Р 54597-2011: Воздух рабочей зоны. Ультрадисперсные аэрозоли, аэрозоли наночастиц и наноструктурированных частиц. Определение характеристик и оценка воздействия при вдыхании — Терминология ГОСТ Р 54597 2011: Воздух рабочей зоны. Ультрадисперсные аэрозоли, аэрозоли наночастиц и наноструктурированных частиц. Определение характеристик и оценка воздействия при вдыхании оригинал документа: 2.4 агломерат (аэрозолей)… … Словарь-справочник терминов нормативно-технической документации
параметр — 3.4 параметр: Одно из измеряемых свойств испытуемого материала. Источник: ГОСТ Р 52205 2004: Угли каменные. Метод спектрометрического определения генетических и технологических параметров … Словарь-справочник терминов нормативно-технической документации
ГОСТ 15895-77: Статистические методы управления качеством продукции. Термины и определения — Терминология ГОСТ 15895 77: Статистические методы управления качеством продукции. Термины и определения оригинал документа: 2.30. k я порядковая статистика x(k) Определения термина из разных документов: k я порядковая статистика 2.44.… … Словарь-справочник терминов нормативно-технической документации
Булева алгебра — Эта статья об алгебраической системе. О разделе математической логики, изучающем высказывания и операции над ними, см. Алгебра логики. Булевой алгеброй[1][2][3] называется непустое множество A с двумя бинарными операциями (аналог конъюнкции),… … Википедия
риск — 2.19 риск (risk): Потенциальная опасность нанесения ущерба организации в результате реализации некоторой угрозы с использованием уязвимостей актива или группы активов. Примечание Определяется как сочетание вероятности события и его последствий.… … Словарь-справочник терминов нормативно-технической документации
П:М — Начинающим · Сообщество · Порталы · Награды · Проекты · Запросы · Оценивание География · История · Общество · Персоналии · Религия · Спорт · Техника · Наука · Искусство · Философия … Википедия
ГОСТ Р ИСО 12716-2009: Контроль неразрушающий. Акустическая эмиссия. Словарь — Терминология ГОСТ Р ИСО 12716 2009: Контроль неразрушающий. Акустическая эмиссия. Словарь оригинал документа: NΣ] (count, event): Число зарегистрированных импульсов дискретной АЭ. Определения термина из разных документов: NΣ] N] (count, acoustic… … Словарь-справочник терминов нормативно-технической документации
Портал:Математика — Начинающим · Сообщество · Порталы · Награды · Проекты · Запросы · Оценивание География · История · Общество · Персоналии · Религия · Спорт · Техника · Наука · Искусство · Философия … Википедия
Математика гармонии — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/22 ноября 2012. Пока процесс обсуждени … Википедия
единица — 1.3.2 единица [объект] (продукции) То, что может быть рассмотрено и описано индивидуально (по 2.1 ГОСТ Р 50779.10). Примечания 1 Единицей может быть, например: изделие; определенное количество материала; услуга, действие или процесс; организация… … Словарь-справочник терминов нормативно-технической документации
Нейтрино — (итал. neutrino, уменьшительное от neutrone нейтрон) электрически нейтральная элементарная частица с массой покоя много меньшей массы электрона (возможно равной нулю), Спином 1/2 (в единицах постоянной Планка ħ) и исчезающе малым, по… … Большая советская энциклопедия
Дискретность в физике и математике. Лекция. Катющи
Дискретный простыми словами – прерывный, разделенный, зернистый, отдельный
— свойство, противопоставляемое непрерывности.
Каждый способен отличить прерывное от непрерывного.
Но если смотреть глубже, то дискретность можно разделить на наружную и внутреннюю.
И гранат например имеет внутреннюю дискретность (состоит из отдельных зёрен), а так же сам может быть рассмотрен как отдельное зерно. На своей поверхности гранат прервался и дальше уже не гранат.
И когда мы например, говорим: «Маша мыла раму», мы должны четко понимать, что Маша так же имеет наружную дискретность – то есть: имеет самостоятельный внешний контур – является самостоятельным объектом.
Так же Маша имеет внутреннюю дискретность – состоит из клеточек. И швабра у Маши так же имеет и внешнюю и внутреннюю дискретность.
И здесь тоже все просто.
Но есть определенные подробности и у многих людей с недискретным, с непрерывным возникают трудности. Попробуем пояснить почему.
Представьте человека, который вырос в глухой степи и по случайному стечению обстоятельств ему никто не рассказал про экскаватор.
И единственное что у него в голове срабатывает:
— Это какие же здесь суслики водятся, что они такую яму вырыли.
И есть вполне конкретные типы задач, который в определенном смысле навязывает воображаемого кимберлитового суслика.
В этом списке и задача на дискретность.
И опять же накладываются представления, что все что нас окружает – состоит из атомов, имеет корпускулярную сущность.
Например, стена её можно пощупать и мы воспринимаем её относительную непрерывность, но жизненный опыт показывает, что у этой непрерывности должен быть внешний край, конец, а значит и стена какая бы длинная она не была в конечном итоге дискретна ( и сама по себе это тоже отдельный элемент). То есть непрерывность (на примере стены) конечна – имеет место наружная дискретность, наружная прерывность.
Следующая позиция №4
Непрерывность материальная, но не вещественная.
Что у нас в природе вообще есть материальное, но не вещественное?
И что материальное может быть фундаментально непрерывным?
И применительно к полю ряд людей вновь, сами не понимая почему – готовы сделать выбор в пользу дискретного решения.
Человеку просто кажется, что и в этом случае неизменно должны быть какие-то дискретные штуки.
В этих случаях помочь не всегда возможно, но на всякий случай сообщаем.
Справочно:
Кимберлитовые суслики не внесены в красную книгу
не находятся под защитой здравого смысла и их можно смело утилизировать.
Для остальных просто напомним, что поле не имеет массы, не имеет вещественности. У поля нет той самой штуки которая может обеспечить внутреннюю дискретность.
Так же у поля нет наружной дискретности. Потому что поле не ограничивается с расстоянием.
И это мы можем наглядно продемонстрировать через график распределения поля в пространстве.
Если мы расположим в пространстве некий единичный источник воздействия, и окружим его некой сферой, то с расширением этой сферы её площадь будет увеличиваться и следовательно будет уменьшаться доля воздействия выпадающая на единицу площади этой сферы.
Формульно это выражается через площадь поверхности сферы
А поскольку речь идет о рассеивании единичного воздействия на поверхность сферы то мы имеем единицу деленную на площадь поверхности сферы, то есть
данное распределение воздействия соответствует приведенному графику.
И в связи с эти мы должны понимать, что даже поле от маленького комаринного магнитика распространяется бесконечно далеко и не имеет внешних границ.
При этом по мере удаления потенциал поля стремится к нулю но никогда через этот нуль не переходит.
Итого применительно к физике мы можем выделить 4 вида дискретных и недискретных состояний.
позиция №1
— Наружная дискретность. Присуща материи разделенной на отдельные фрагменты. Материя имеющая внешние границы.
Позиция № 2
— внутренняя дискретность в рамках некой непрерывности
— присуща материи имеющей общую протяженную вещественную непрерывность, и внутреннее дискретное строение в форме отдельных элементов.
В эту категорию попадают все объекты состоящие из вещества, которые внешне воспринимаются как непрерывные, но по своей структуре состоят из более мелких частей.
Позиция № 3
непрерывность нематериальная (присущая пространству) не имеющая внутренней структуры (внутренней дискретности).
позиция №4
Непрерывность материальная невещественная (присущая физическому полю).
Данные четыре позиции желательно твёрдо запомнить. Это облегчит понимание физики в целом.
Собственно всё.
С вами был Виктор Катющик.
Подписывайтесь на видеоканал.
Следите за нашими публикациями.
Дискретность
Области применения
Понятие дискретности применяется в следующих областях:
См. также
Полезное
Смотреть что такое «Дискретность» в других словарях:
дискретность — и, ж. discret. 1. устар. Сдержанность, молчаливость. Прошло несколько недель, прежде чем мне удалось убедить моих подозрительных менторов в моей полной дискретности с первого момента. А. Романов Кн. восп. 69. Блестящие способности, врожденная… … Исторический словарь галлицизмов русского языка
дискретность — раздельность, целочисленность, прерывистость Словарь русских синонимов. дискретность сущ., кол во синонимов: 5 • дробность (9) • … Словарь синонимов
ДИСКРЕТНОСТЬ — противоположность непрерывности; в физике и химии Д. означает зернистость строения материи, её атомистичность, напр. дискретность уровней энергии электрона … Большая политехническая энциклопедия
ДИСКРЕТНОСТЬ — (от латинского discretus разделенный, прерывистый), прерывность; противопоставляется непрерывности. Например, дискретное изменение какой либо величины во времени изменение, происходящее через некоторые промежутки времени (скачками) … Современная энциклопедия
ДИСКРЕТНОСТЬ — (от лат. discretus разделенный прерывистый), прерывность; противопоставляется непрерывности. Напр., дискретное изменение какой либо величины во времени изменение, происходящее через некоторые промежутки времени (скачками). См. также Прерывность и … Большой Энциклопедический словарь
дискретность — ДИСКРЕТНЫЙ, ая, ое; тен, тна (книжн.). Раздельный, состоящий из отдельных частей. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ДИСКРЕТНОСТЬ — (от лат. discretus разделённый, прерывистый), прерывность; противопоставляется непрерывности. Напр., дискретное изменение к. л. величины во времени это изменение, происходящее через определ. промежутки времени (скачками). Д. означает… … Философская энциклопедия
ДИСКРЕТНОСТЬ — [англ. discrete Словарь иностранных слов русского языка
ДИСКРЕТНОСТЬ — (от лат. discretus разделенный, прерывистый) англ. discreteness; нем. Diskretheit. Свойство предметов, явлений и процессов, характеризующихся прерывностью неделимых единиц, их скачкообразными изменениями во времени. Antinazi. Энциклопедия… … Энциклопедия социологии
Дискретность — [discretion] прерывность. Например, изменение экономических показателей во времени всегда имеет прерывный характер, поскольку происходит скачками от одной даты (года, месяца и т.д.) к другой. Понятие Д. противопоставляется понятию непрерывности.… … Экономико-математический словарь
ДИСКРЕТНОСТЬ — (от латинского discretus разделенный, прерывистый) Свойство, противопоставляемое непрерывности, прерывность. Под дискретностью понимают: Нечто, изменяющиеся между несколькими различными стабильными состояниями подобно выключателю, который может… … Словарь бизнес-терминов
Что такое дискретность (дискретная математика, сигнал, величины, видеокарты, а так же дискретность в биологии)
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Знать все обо всем попросту невозможно. Человек на протяжении всей жизни стремится познать себя и окружающую его действительность.
Вот и сегодня мы продолжим свой познавательный процесс, поговорим о новом (для многих) термине – « дискретность», и о сферах, где он применяется.
Дискретность – это …
Наш мир непрерывен, мы живем в постоянно меняющемся времени и пространстве. Наша жизнь тоже непрерывна до своего конечного момента. Согласитесь, невозможно сейчас жить, через час не жить, а потом вновь возродиться.
В противопоставлении непрерывности существует дискретность. В переводе с «вечно живого» латинского языка «дискретность» (discretus) обозначает прерывность, разделенность.
Дискре́тность (от лат. discretus — разделённый, прерывистый) — свойство, противопоставляемое непрерывности, прерывистость. Синонимы к слову дискретный: корпускулярный, отдельный, прерывистый, раздельный и т. п.
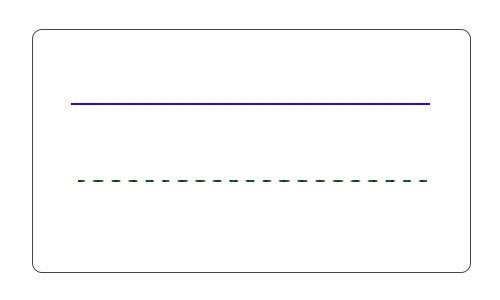
Например, линия непрерывна (на определенном промежутке), пунктир – прерывистая линия. Поэтому пунктир можно назвать дискретной линией. Проиллюстрирую понятие дискретности:
Дискретность можно толковать следующим образом:
Далее проанализируем особенности применения термина в различных областях.
Дискретная математика
Если коротко и простыми словами, то дискретная математика (ДМ)– это наука, которые изучает математические объекты, принимающие отдельные (дискретные) значения.
ДМ условно подразделяется на пять направлений:
Дискретная величина
Дискретность какой-либо величины подразумевает, что ее значения можно пронумеровать, измерить и посчитать.
Такими величинами оперирует, например, экономика. Различные экономические показатели фиксируют и рассчитывают с определенной периодичностью (например, раз в месяц, квартал, полугодие и т.д.). Таким образом, изменение показателей происходит не непрерывно во времени, а как бы «скачками» через установленные интервалы времени.
Дискретность в информатике
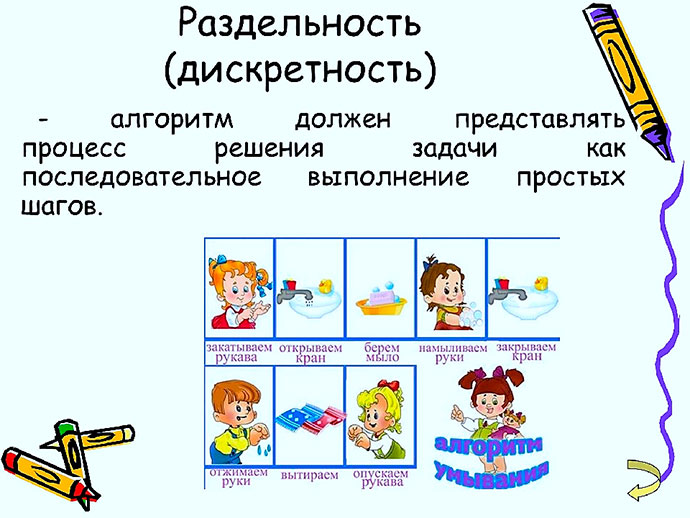
Программирование – это создание программ с использованием различных алгоритмов и языков программирования. Алгоритмы являются дискретными объектами, потому как представляют собой четкое последовательное выполнение ранее разработанных упрощенных шагов-действий (подпрограмм).
Только исполнение шага № 1 дает возможность выполнить шаг № 2 и т.д. Таким образом, этот процесс дискретен.
Как пример – алгоритм умывания (компьютерные программы создаются по тому же принципу):
Дискретная видеокарта
Видеокарта – один из важнейших элементов компьютера, отвечающий за визуализацию информации. Конструкция компа может быть оснащена либо интегрированной (встроенной) видеокартой, либо дискретной. Встроенная размещается в процессоре или на материнской плате, т.е. она неотделима от конкретного компьютера.
Дискретная видеокарта выполнена на отдельной плате, снабжена индивидуальным графическим процессором и памятью. Поэтому она более производительна, чем интегрированная.
Часто в компьютерах применяются видеокарты обоих видов, что позволяет пользователю при необходимости переключаться с одной на другую.
Дискретность в биологии
Все биологические объекты состоят из отдельных (дискретных) «кирпичиков», которые в совокупности образуют единый организм. Например, скелет человека состоит из костей, кости –из костной ткани, она, в свою очередь – из клеток.
Автор статьи: Елена Копейкина
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Благодарю за дискретное изложение материала
Дискретная система оценивания
РЕСПУБЛИК (я)5 G 05 В 17/00, G 05 F 1/00
ПО ИЗОБРЕТЕНИЯМ И ОТКРЫТИЯМ
ПРИ ГКНТ СССР, «,)О il i! g
ОПИСАНИЕ ИЗОБРЕТЕНИЯ л
X(n) X(n) К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ (21) 4756238/24 (22) 03.11.89 (46) 15.04.92. 6юл. М 14 (72) Ю.А.Пушкарев, А.А.Шалаевский и
В.И.Ищенко (53) 62-50(088.8) (56) Гришин Ю.П., Казаринов Ю,М. Динамические системы, устойчивые к отказам. М.:
Радио, 1985, с. 19. (54) ДИСКРЕТНАЯ СИСТЕМА ОЦЕНИВАНИЯ (57) Изобретение относится к радиотехнике и автоматике и может быть использовано в
° ЯЛ 1727110 А1 радиолокации для оптимальной линейной оценки параметров движения летательных аппаратов. Цель изобретения — повышение динамической точности системы. Дискретная система оценивания содержит первый вычитатель 1, блок 2 коррекции, сумматор 3, первый блок 4 задержки, блок 5 экстраполяции, второй 6 и третий 7 вычитатели, второй блок 8 задержки, усилитель 9, счетчик 10, двухканальный мультиплексор 11, компаратор 12; умножитель 13, сумматор 14, элементы 15 — 17 памяти коэффициентов. Цель изобретения достигается за счет введения элементов и блоков 6-17. 3 ил.
Изобретение относится к радиотехнике и автоматике, в частности может использоваться в радиолокации для оптимальной линейной оценки параметров движения л етател ьн ых объектов.
Известны дискретные системы оценивания, предназначенные для оценивания параметров движения объектов.
Недостатком систем является отсутствие возможности качественно управлять динамической точностью в переходном режиме.
Известна также дискретная система оценивания, содержащая последовательно соединенные элемент сравнения, блок коррекции, сумматор, блок задержки, блок экстраполяции, блок обратной связи, Данная система имеет возможность оптимально оценивать параметры движения объектов в установившемся режиме. Недостатком данной системы является невысокая динамическая точность в переходном режиме.
Наиболее близкой к предлагаемой является дискретная система оценивания, которая имеет воэможность оптимальным образом оценивать параметры движения обьектов в установившемся режиме. Она содержит последовательно соединенные элемент сравнения, блок коррекции, сумматор, блок задержки, блок экстраполяции, выход которого соединен с вторыми входами элемента сравнения и сумматора.
Недостатком данной системы является низкая динамическая точность в переходном режиме.
Цель изобретения — повышение динамической точности системы в переходном режиме.
Поставленная цель достигается за счет введения в известную систему двух вычитателей, второго сумматора, трех элементов памяти коэффициентов, счетчика, компаратора, усилителя, умножителя, второго блока задержки и двухканального мультиплексора.
На фиг. 1 изображена структурная схема системы оценивания; на фиг. 2 — структурная схема блока экстраполяции.
Дискретная система оценивания (фиг. 1) содержит вычитатели 1, 6 и 7, блок 2 коррекции, сумматоры 3 и 14, блоки 4 и 8 задержки с операторами задержки z, блок 5 экстраполяции, усилитель 9, счетчик 10, двухканальный мультиплексор 11, компаратор 12, умножитель 13, элементы 15 — 17 памяти коэффициентов, В статическом состоянии система оценивания характеризуется следующими связями: содержит последовательно соединенные вычитатель 1, блок 2 коррек5
55 ции, сумматор 3, блок 4 задержки, блок 5 экстраполяции. Первый вход вычитателя 1 и выход сумматора 3 являются соответственно информационным входом и выходом дискретной системы оценивания. Кроме того, система оценивания содержит вычитатели 6 и 7, сумматор 14, элементы 15 — 17 памяти коэффициентов, счетчик 10, компаратор 12, усилитель 9, умножитель 13, блок 8 задержки и двухканальный мультиплексор 11. Выход вычитателя 1 через последовательно соединенные блок 8 задержки и усилитель 9 подключен к первой группе информационныхх входов мультиплексора 11, соединенного второй группой информационных входов с выходами. элементов 15 — 17 памяти коэффициентов, адресным входом — с выходом счетчика 10 и первым входом компаратора
12. Первый выход блока 5 экстраполяции подключен к первому входу умножителя 13, соединенного вторым входом с первым выходом мультиплексора 11, а выходом — с первыми входами сумматора 14 и вычитателя 6. Второй выход блока 5 экстраполяции подключен к первому входу вычитателя 7 и второму входу вычитателя 6, соединенного выходом с вторым входом вычитателя 1.
Второй выход мультиплексора 11 подключен к второму входу сумматора 14, соединенного выходом с вторым входом вычитателя 7, выход которого подключен к второму входу сумматора 3. Второй вход компаратора 12 соединен с шиной задания числа шагов, а выход — с информационным входом счетчика 10, тактовый вход которого является тактовым входом дискретной системы оценивания.
При работе устройства возможны два режима работы; переходный и установившийся.
В установившемся режиме устройство работает следующим образом.
Входной сигнал системы Х(п), представляющий собой сумму детерминированной составляющей вх(п), центрированной случайной составляющей X(n) и ошибок измерения f(n) (помехи), поступает на первый вход вычитателя 1, на его второй вход подается экстраполированное значение входного сигнала Хэ(п). В установившемся режиме блоки 8-17 системы не работают, поэтому информация на первом входе вычитателя 6 и втором входе вычитателя 7 отсутствует. В этом случае экстраполированное значение входного сигнала X>(n), сформированное блоком 5, проходит через вычитатели 6 и 7 без изменений. На выходе вычитателя 1 имеем сигнал невязки 0(п), который поступает на блок 2 коррекции. На выходе сумматора 3 имеем сигнал оценки Х(п):
Первые два члена в правой части выражения (1) являются сигналом Хэ(п), сформированным блоком 5 экстраполяции. Блок 5 экстраполяции синтезирован на основании 5 известного метода «трех полиномов» из условия: входное воздействие на систему имеет вид
10 где mx(n) — детерминированная составляющая задающего воздействия X(n);
Х(п) — его центрированная случайная составляющая;
f(n) — центрированная возмущающая со- 15 ставляющая (ошибки наблюдения).
v = 2, а следовательно из метода «трех полиномов» определим полиномы
A(Z,n) = ao(nX1 — 2 ) и
B(Z,п) = bp(n)(1 Z ). (3) Характеристический полином выбираем из условия устойчивости системы.
C(Z,n) = ао(п) — 2bp(n)Z + bp(n)Z
Используя выражение для оценки метода «трех полиномов» (.(Z,и1- S(Z,n)
4М ао и где U(n) — невязка, а— о и
После преобразования (6) получим выражение для оценки в операторном виде 50
/ где Xs(2) = 2X(Z)Z X(Z)Z — экстраполированное значение координаты;
0(2)(1-Ь (и)) = (.)(2)К(п) — корректировочное значение.
Блок 5 экстраполяции, структурная схема которого изображена на фиг. 2, содержит блоки 18 и 19 задержки с оператором задержки Z усилители 20 и 22 с коэффициентами усиления «два» и вычитатели 21 и 23.
На основании проведенного синтеза уравнения(7) построена часть блока 5, включающая в себя блок 18 задержки, усилитель
20, вычитатель 21. Эта часть блока 5 используется устройством при работе как в установившемся, так и в переходном режиме.
Блоки 19, 22 и 23 используются устройством при работе только в переходном режиме.
Входным сигналом для блока 5 экстраполяции является сигнал с выхода блока задержки Х(п-1), Сигнал с первого выхода блока 5 поступает на первый вход умножителя 13, а сигнал с второго выхода в виде
X (n) — на первый вход вычитателя 7 и на второй вход вычитателя 6, через которые поступает соответственно на вторые входы сумматора 3 и вычитателя 1. Сигнал Х(п) формируется в виде (1), сигнал невязки U(n) — в следующем виде: ю/ и л
U(n) = Х(п) — 2X(n — 1) + X(n-2). (8) Прежде, чем описывать работу устройства в переходном режиме, необходимо отметить, что в замкнутых системах оценивания, использующих для сглаживания (фильтрации) и управления только одни и те же весовые коэффициенты, существует противоречие между условиями уменьшения флюктуационных ошибок (условиями фильтрации) и условиями повышения динамической точности в переходном режиме.
Это противоречие может быть разрешено с помощью введения дополнительных весовых коэффициентов по каналу управления.
Тогда можно добиваться высокого качества переходного процесса как по каналу управления, так и по каналу оценивания, не увеличивая при этом флюктуационные ошибки.
В связи с изложенным полиномы A(Z,ï), B(Z,n), C(Z,n) представим в виде
U(n) = X(n) — Хэ(п), (15) 10 имеем
Из(11) при условии, что (12) имеем
C(-1)(Z,n) U (n) = U,),(n), A(Z,n) Хо(п) = (.4ын(п), (13) Так как Г1+ F1= 1, то (16) Поэтому
При оценивании процесса(2) обеспечим требуемое качество переходного процесса по критерию где V1M» = мин U „(1), Чгм» = мин U „(2) и г » г т.д„
U() — переходная составляющая ошибки наблюдения.
Для отыскания оптимальных коэффициентов а1 р (и) обратимся к методу «трех полиномов» для невязки
Up(n) = С(-1)(Z,n) Up(n) + A(Z,n) Хо(п), где полином C(-1)(Z,n) — это полином C(Z,n) без свободного слагаемого.
Следовательно, есть свободная и вынужденная составляющие динамической ошибки в переходном режиме. И та и другая составляющие зависят от коэффициентов а1(п), причем противоречивым образом. Поэтому существуют оптимальные значения коэффициентов а1оР (n), удОВЛЕтВОряЮщИЕ КрИтЕрИЮ (10).
Для отыскания минимальных значений
VM» критерия качества I вводятся весовые коэффициенты Г и F по свободной и вынужденной составляющей соответственно.
Из (11) с учетом (12) и (9) получим следующее разностное уравнение:
35 (Е, U(o) „) I(..; ; a,(з) х,(o) Fâ.
Дальнейшее решение задачи основывается на принципе оптимальности Белмана, согласно которому каждое последующее оптимальное значение коэффициента a1(n)
40 получается относительно предыдущего состояния, полученного оптимальным образом, На первом шаге оптимизации имеем
U п(1) р = (а1 р (1) — 2Ьо(1)) Х p(0)l + (а1ор (1) — 2)г Х p(0)F1.
+a((-2a,®3x оp(0)(-aF,) =D Р а1ь,(6Ю () „P Ã,. 4,3
Ba,(ц= Р ьИ («-). (ь а () ((о)г,=О ор1 2.bo()u (2) „ Гз ° 7, (1 8) При выбранных полиномах А(2,п), B(Z,n), C(Z,ï) коэффициент а1(п) не входит в управление. Это приводит к ухудшению качества фильтрации. Чтобы снять этот недостаток, необходимо в разнице полиномов
C(Z,n)-B(Z,ï) исключить слагаемые, содержащие коэффициенты а1(п). Это можно сделать лишь в том случае, если полином C(z,ï) и B(Z, N ) включают в себя коэффициенты
10 Здесь выражение для функции F (z) (программы управления) будет иметь вид
15 и, следовательно, алгоритм управления примет вид п h h
Хэ(п) = 2X(n-1)-X(n-2)-а 1(п)Х(п-1) + л A
20 + 2а1(п) Х (n — 2)-а1(п)Х(п-3). (23) Таким образом, выбор полиномов А и В в соответствии с выражением (19) создает условия для оптимальных переходных про25 цессов без нарушения условий фильтрации
В переходном режиме устройство работает следующим образом, В момент включения устройства на вход системы поступает ступенчатое воздейст30 вие вида (12), обусловленное априорной неопределенностью состояния обьекта. Для того, чтобы улучшить качество переходного процесса заранее по формулам (16) — (1 8), вычисляются коэффициенты а1(1), а1(2), а1(3) и
35 записываются в блоки 15-17. Количество шагов, равное трем, определяется порядком характеристического полинома при ступенчатом воздействии.
Процесс управления в переходном ре40 жиме реализуется устройством при помощи блока 8 задержки, усилителя 9 с коэффициентом усиления Ь1(п), счетчика 10, двухканального мультиплексора 11, компаратора
12, умножителя 13, сумматора 14, элемента
45 15 хранения коэффициента а1(1), элемента
16 хранения коэффициента а1(2), элемента
17 хранения коэффициента а1(3).
Перед началом работы устройства на второй вход компаратора 12 подается код N
50 числа шагов работы системы в переходном режиме, Для рассматриваемого случая N =
3. На вход счетчика 10 поступает последовательность импульсов пТ, синхронная моментам выдачи информации на обработку.
56 Выходные сигналы счетчика 10 поступают на адресный вход мультиплексора 11 (в качестве которого может быть использована, например, микросхема К155КП2). В первом такте коэффициент а1(1) считывается из элемента 15 памяти и проходит через мульти1727110
55 плексор 11 на второй вход умножителя 13, в котором умножается на сигнал X(n-I) — 2X(n2)+ Х(п — 3), сформированный блоками 18, 19 и 20 и вычитателем 23 блока 5. На выходе умножителя 1 формируется сигнал
a1(1)X(n-1) — 2а1(1)Х(п — 2) + а1(1)Х)п — 3). B тоже время по второму каналу мультиплексора 11 поступает сигнал b (n) принимались Х =
30 м, Т = 0,1 с. Результаты моделирования приведены на фиг. 3, где пунктиром показаны ошибки оценки в переходном режиме для системы с а (п) = О, а сплошной — с использованием а (п) О, где коэффициенты а (п) принимали значение; 2; 0,615; 2 соответственно, Данным значениям соответствуют весовые коэффициенты Г = F=
Анализ результатов моделирования показал, что применение блоков 8 — 17 позволяет повысить динамическую точность системы в переходном режиме. Время регулирования переходного процесса уменьши5
Дискретная система оценивания, содержащая последовательно соединенные первый вычитатель, блок коррекции, первый сумматор, первый блок задержки, блок экстраполяции, первый вход первого вычитателя и выход первого сумматора являются соответственно информационными входом и выходом дискретной системы оценивания, отл ича ющая с ятем, что, с целью повышения динамической точности системы, в нее введены два вычитателя, второй сумматор, три элемента памяти коэффициентов, счетчик, компаратор, усилитель, умножитель, второй блок задержки и двухканальный мультиплексор, выход первого вычитателя через последовательно соединенные второй блок задержки и усилитель подключен к первой группе,информационных входов двухканального мультиплексора, соединенного второй группой информационных входов с выходами элементов памяти коэффициентов, адресным входом — с выходом счетчика и первым входом компаратора, первый выход блока экстраполяции подключен к первому входу умножителя, соединенного вторым входом с первым выходом двухканального мультиплексора, а выходом — с первыми входами второго сумматора и второго вычитателя, второй выход блока экстраполяции подключен к первому входу третьего вычитателя и второму входу второго вычитателя, соединенного выходом с вторым входом первого вычитателя, второй выход двухканального мультиплексора подключен к второму входу второго сумматора, соединенного выходом с вторым входом третьего вычитателя, выход которого подключен к второму входу первого сумматора, второй вход компаратора соединен с шиной задания числа шагов, а выход — с информационным входом счетчика, тактовый вход которого является тактовым входом дискретной системы оценивания.
Техред М.Моргентал Корректор С.Лыжова
Заказ 1278 Тираж Подписное
ВНИИПИ Государственного комитета по изобретениям и открытиям при ГКНТ СССР
113035, Москва, Ж-35, Раушская наб., 4/5
Производственно-издательский комбинат «Патент», г. Ужгород, ул.Гагарина, 101