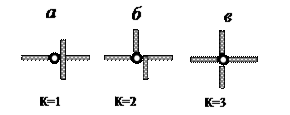что такое диск в механике строительной

Понятия и характеристики диска, кинематической связи, шарнира, опор.

Любое заведамо неизменяемое тело называется диском(стержень и Земля это тоже диски).Любое тело, отнимающее у системы одну степень свободы, называется кинетической связью. Строительное сооружение,в классической стр. механике представляет собой системы состоящие из ломанных или прямолинейных стержней,которые соединяются между собой при помощи шарнира,а с основанием при помощи опор,при этом в каждом узле.в ктором соединяются стержни системы может быть несколько простых или одиночных шарниров.

Определение степеней свободы различных систпем.

Степень свободы системы пределяется:1-для любых систем [W=Ш-3К], Ш-кол-во простых шарниров, включая шарниры в опорах,К-кол-во замкнутых контуров в системе;2—для любых систем, заисключение с полностью замкнутыми жесткими контурами.[W=3Д-2Ш-Сₒ],Д-кол-во дисков в системе,кроме стержней в опорах,Ш-кол-во простых или одиночных шарниров,кроме шарниров в опоре,Сₒ-кол-во связей в опорах;3)—для ферм [ W=2y-C- Сₒ], y-кол-во узлов в ферме,С-кол-во стержней в ферме,Сₒ-кол-во связей в опорах;4)—для систем состоящих из 1 диска [W=3- Сₒ]; 5)-в зависимости от взаимосвязи эл-та между собой и от видов опор в системе возможно 3 варианта степени свободы:W 0—система-механизм и не может быть использована в расчетах.

Классификация сооружений в зависимости от значений степени свободы.

В зависимости о взаимосвязей элементов системы между собой и от видов опор в системе, возможны три варианта степени свободы: w 0- система –механизм и не может быть использ.в расчетах.

10. Принципы образования геометрически неизменяемых систем.

Принципы: 1. Если три диска соединены между собой последовательно при помощи тремя шарнирами не лежащих на одной прямой, то система геометрически неизменяема. 2. Если точка соедин. с диском при помощи двух стержней, то такая система геометр неизменяемая. 3. Если два диска соединены между собой при помощи трех стержней не параллельных и не пересекаются в одной точке, то такая система геометрически неизменяема. 4. Если три диска соединены между собой при помощи шести стержней, каждые два из которых соед. при помощи двух не параллельных стержней, то такая система геометрически неизменяема.

Понятия фиктивного шарнира и его свойства и использование при геометрическом анализе изменяемых и неизменяемых систем

Мгновенно изменяемые сис-мы и их св-ва.

Мгновенно изменяемой называется особая конфигурация, в которой геометрически неизменяемая сис-ма, выполненная из абсолютно недеформируемых элементов, обладает бесконечно малой подвижностью по сравнению со смежными абсолютно неподвижными конфигурациями.

Мгновенно изменяемые сис-мы характеризуются повышенной деформативностью по сравнению с геометрически неизменяемыми сис-ми.

Если в сис-ме с нулевой степенью свободы (W=0), т.е. в сис-ме формально геометрически неизменяемой и статически определимой, могут быть начальные усилия, то такая сис-ма мгновенно изменяема или частично статически неопределима, а частично геометрически изменяема. В последнем случае необходимо провести кинематический анализ сис-мы по фрагментам.

Геометрические признаки мгновенно изменяемых систем.

Признаки: 1. Если три диска соединены между собой при помощи трех шарниров, лежащих на одной прямой, то такая система мгновенно изменяема. 2. Если два диска соединены при помощи трех стержней. Пересекаются в одной точке, то система мгновенно изменяема. 3. Если три диска соединены при помощи трех параллельных стержней, то система мгновенно изменяема.

Источник

Строительная механика

Главное меню

Присоединяйтесь

Кинематический анализ. Основная формула кинематического анализа

Внешняя нагрузка, воздействующая на сооружение, может вызвать большие перемещения отдельных элементов конструкции, в результате чего оно может быть разрушено, следовательно, перемещения сооружения должны быть очень малыми.

Кинематический анализ – это анализ геометрической структуры сооружения для того, чтобы не допустить возможности возникновения больших перемещений.

В строительной механике при выполнении кинематического анализа внешняя нагрузка не учитывается, а все элементы конструкции считаются жесткими.

В кинематическом анализе выделяют следующие типы расчетных схем:

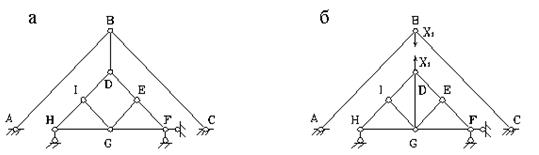
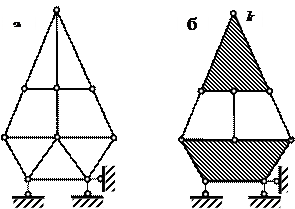
1) Геометрически неизменяемая система – это система, элементы которой могут перемещаться только за счет своей деформации. Одним из вариантов такой системы является шарнирный треугольник (рис. 1, а).

2) Геометрически изменяемая система – это система, элементы которой могут перемещаться даже без деформаций. В качестве примера такой системы можно привести шарнирный четырехугольник (рис. 1, б).

3) Мгновенно изменяемая система – система, элементы которой могут получать только мгновенные перемещения (рис. 1, в).

Рисунок 1. Типы расчетных схем в кинематическом анализе

Кинематические свойства инженерной конструкции определяют путем расчета числа ее степеней свободы.

Число степеней свободы (W) – это минимальное количество координат, требуемое для определения места нахождения любого элемента конструкции.

Кинематические связи (внутренние и внешние) должны обеспечивать неподвижность конструкции относительно фундамента, а также неизменяемость ее внутренней геометрической структуры.

В случае, если при исключении одной связи из неизменяемой конструкция превращается в изменяемой, то эта связь называется необходимой.

В случае, если при удалении одной связи конструкция остается неизменяемой, то связь называется избыточной.

Число степеней свободы для плоской стержневой системы рассчитывается по формуле, называемой основной формулой кинематического анализа :

Диск (Д) – неизменяемая часть конструкции, представляющая собой жесткий неподвижный элемент;

Шарнир (Ш) – связь, позволяющая соединяемым ею дискам поворачиваться друг относительно друга;

Опорный стержень (С₀) – число реакций, которые могут возникать во всех связях ( внутренних и внешних ) данной конструкции.

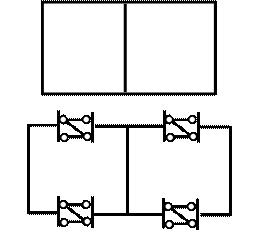
Шарнир, соединяющий два диска, называется простым шарниром (рис. 2, а).

Шарнир, соединяющий несколько дисков, называется сложным шарниром (рис. 2, б).

Сложный шарнир равен ( k –1 ) простому шарниру, где k – число дисков, соединяемых данным шарниром.

Рисунок 2. Сложный и простой шарниры

При расчете по основной формуле кинематического анализа возможны следующие результаты:

1) W>0 – такая система является геометрически изменяемой и такая конструкция не может служить в качестве инженерного сооружения;

2) W=0 – в схеме введено необходимое число связей и если они введены верно, то система неизменяема и статически определима;

Источник

Расчетные схемы сооружений. Кинематический анализ. Расчет статически определимых балок. Линии влияния. Расчет плоских ферм. Расчет трехшарнирных систем

Страницы работы

Содержание работы

Тема 1. Расчетные схемы сооружений.

1. Объект изучения строительной механики

Строительная механика изучает методы расчета механических систем на прочность, жесткость и устойчивость при статических и динамических воздействиях.

2. Основные уравнения строительной механики

Уравнения равновесия связывают внешние и внутренние силы, которые входят в них линейно, т. е. в первой степени.

Уравнения совместности деформаций связывают деформации с перемещениями. В общем случае они нелинейные, но их можно считать линейными в случае малых деформаций. Исключение – гибкие конструкции.

Физические уравнения связывают усилия с деформациями. Могут быть линейными или нелинейными в зависимости от принятой физической модели материала.

3. Что такое физическая модель материала?

Это оценка механического поведения материала, выраженная математически, т. е. с помощью функции s = f(e). Для наглядности представляют в виде графиков. Вместо действительных диаграмм пользуются идеализированными схемами. Наиболее часто применяются модель линейно-упругого и линейно-упруго-пластического тела (диаграмма Прандтля).

4. Какие допущения используются в статике стержневых систем?

В основной части курса изучаются линейно деформируемые системы, для которых физические уравнения и уравнения совместности деформаций линейные. Для каждого стержня системы справедливы гипотезы и допущения сопротивления материалов:

§ гипотеза однородности и сплошности

§ гипотеза об идеальной упругости материала

§ допущение о справедливости закона Гука

§ гипотеза плоских сечений Бернулли

§ допущение о малости деформаций

§ принцип независимости действия сил

Некоторые из этих допущений несправедливы, например, для нелинейно упругих, упругопластических систем, гибких конструкций.

5. Что такое расчетная схема сооружения?

Это упрощенное изображение сооружения, учитывающее только основные данные, которые определяют его поведение под нагрузкой. Для одной и той же конструкции могут быть приняты различные расчетные схемы. Это зависит от требуемой точности расчета, имеющегося времени, наличия тех или иных вычислительных средств.

6. Принципы составления расчетной схемы стержневой системы.

§ Стержни заменяются осевыми линиями;

§ нагрузки с поверхности элементов переносятся на оси;

§ поперечные сечения стержней независимо от их формы характеризуются численными значениями площадей и моментов инерции;

§ реальные опорные устройства и связи между элементами заменяются идеальными связями.

7. Дать определение балки (фермы, арки, рамы, висячей системы). На что она работает?

Балочные конструкции характеризуются тем, что в горизонтальных системах при действии вертикальной нагрузки в опорах возникают только вертикальные реакции. Работают на изгиб.

Арочные конструкции состоят из криволинейных стержней, выпуклость которых направлена в сторону, противоположную действию нагрузки. Вертикальная нагрузка вызывает в опорах наклонные реакции. Работают на внецентренное сжатие.

Рамы – стержневые системы с жестким соединением прямолинейных элементов во всех или некоторых узлах. Стержни рамы работают на изгиб с растяжением или сжатием.

Фермы – системы прямолинейных стержней, которые при узловой передаче нагрузки испытывают только деформацию растяжения или сжатия.

Висячие системы представляют собой конструкции, в которых гибкие элементы (ванты) работают на растяжение.

8. Какие системы называются статически определимыми?

Такие, для которых все реакции связей и внутренние силы можно определить из уравнений статического равновесия.

9. Какие системы называются статически неопределимыми?

Такие, для которых реакции связей и внутренние усилия нельзя найти, пользуясь только уравнениями статики. Дополнительно приходится использовать уравнения совместности деформаций.

10. Что такое расчет по недеформированной схеме?

Такой расчет, когда уравнения равновесия для определения усилий составляются по расчетной схеме в недеформированном состоянии. Справедлив для большинства задач статики стержневых систем. Исключение – расчет гибких конструкций; расчет стержней на устойчивость при продольном и продольно-поперечном изгибе.

11. Какая система называется геометрически неизменяемой?

Такая система, которая допускает взаимные перемещения составляющих ее элементов лишь за счет деформации самих элементов.

12. Основное свойство геометрически неизменяемой системы

Она способна принимать на себя и уравновешивать внутренними силами любые нагрузки до разрушения материала.

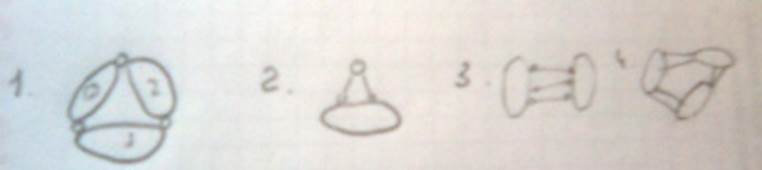
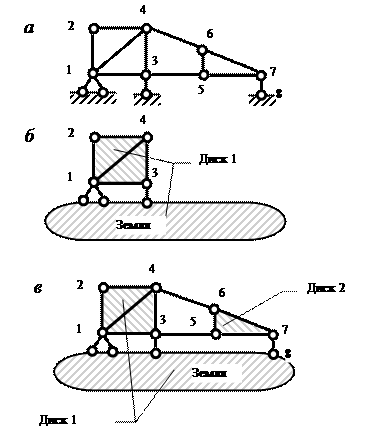
Диском называется элемент плоской системы, геометрическая неизменяемость которого доказана или очевидна. Простейшим диском является стержень (брус, балка). Земля (основание) считается неподвижным диском.

14. Какая система называется геометрически изменяемой?

Такая система, у которой конечные взаимные перемещения элементов возможны без их деформации. Эти системы представляют собой механизмы и применяются в различных машинах.

Источник

Что такое диск в механике строительной

3. Примеры кинематического анализа

3.1. Правила образования геометрически неизменяемых систем

Любую геометрически неизменяемую часть системы назовем диском.

П равило 1: узел присоединяется к диску двумя связями, не лежащими на одной прямой (рис. 3.1).

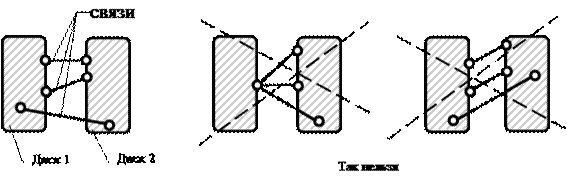
Правило 2: диск соединяется с другим диском тремя связями, не пересекающимися в одной точке и не параллельными друг другу (рис. 3.2).

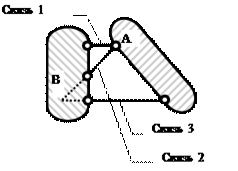
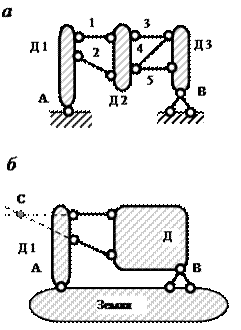
Точка пересечения двух связей может рассматриваться как шарнир – действительный или фиктивный. Поэтому правило 2 можно трактовать как соединение двух дисков с помощью шарнира и одной связи, не проходящей через шарнир. Например, два диска, показанные на рис. 3.3, соединены действительным шарниром А и связью 3. Можно также считать, что диски соединены фиктивным шарниром В и связью 1.

Рис.3.1. Присоединение узла к диску

Рис.3.2. Соединение двух дисков тремя связями

Рис.3.3. Соединение двух дисков шарниром и стержнем:

А – действительный шарнир; В – фиктивный шарнир

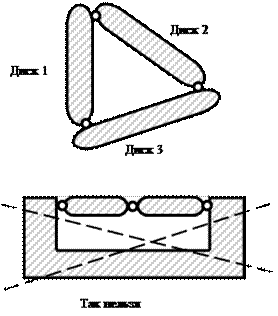
Правило 3: три диска соединяются друг с другом тремя шарнирами, не лежащими на одной прямой (рис. 3.4). Шарниры могут быть действительными или фиктивными.

Рис.3.4. Соединение трех дисков тремя шарнирами

Если какое-то из указанных правил нарушается, система оказывается геометрически изменяемой или мгновенно изменяемой.

Если система образована с использованием перечисленных правил, она будет обязательно геометрически неизменяемой.

Если при кинематическом анализе в геометрически неизменяемой системе обнаруживается n избыточных связей, то система оказывается n раз статически неопределимой. При отсутствии избыточных связей система является статически определимой.

Системы, образование которых подчиняется указанным правилам, называются системами простого образования. Есть системы, порядок образования которых не может быть установлен с помощью упомянутых выше правил. Для кинематического анализа таких систем применяют иные методы, например метод замены связей, которые в настоящем пособии не рассматриваются.

3.2. Степень свободы системы

Степенью свободы системы W называется число независимых параметров, определяющих положение системы в пространстве.

Д – число дисков, из которых образована система;

Ш – число простых шарниров, соединяющих диски между собой;

С – число связей, соединяющих диски между собой;

С _О – число опорных связей, соединяющих диски с землей.

Простым шарниром называется шарнир, соединяющий два диска, такой шарнир эквивалентен двум связям. Если шарнир соединяет d дисков, то он называетсякратным шарниром и его кратность К =d–1 показывает, скольким простым шарнирам он эквивалентен (рис. 3.5).

Рис.3.5. Простой (а) и кратные (б, в) шарниры

Для произвольной плоской системы

причем диски не должны содержать избыточные связи.

Для ферм с шарнирными узлами степень свободы можно определить по более простой формуле

где У – число узлов фермы; С – число стержней фермы; С_О – число опорных связей.

Если W > 0, то система геометрически изменяемая.

Если W = 0, то система геометрически неизменяемая и статически определимая.

Важно знать, что условия геометрической неизменяемости W = 0 и W

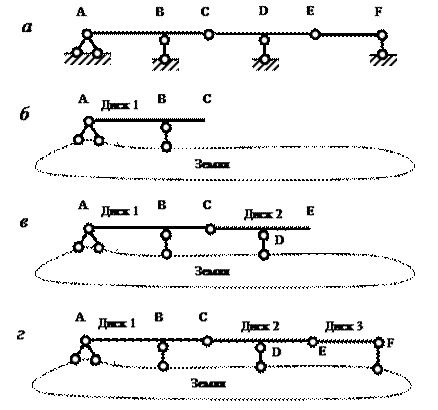
Пример 1. Кинематический анализ балки (рис. 3.6, а).

Балка собирается в такой последовательности:

1-й этап. К земле, как к диску, присоединяется Диск 1 (стержень АВС) с помощью трех связей (правило 2, рис. 3.6, б).

Рис.3.6. Последовательность сборки балки

2-й этап. К образовавшейся системе «Земля + Диск 1», как к единому диску, присоединяется Диск 2 (стержень CDE ) с помощью шарнира С и опорной связи в точке D (вариант правила 2, рис. 3.6, в).

3-й этап. К образовавшейся системе «Земля + Диск 1 + Диск 2», как к единому диску, присоединяется Диск 3 (стержень EF ) с помощью шарнира E и опорной связи в точке F (вариант правила 2, рис. 3.6, г). Этим и заканчивается сборка балки.

Поскольку образование балки (рис. 3.6, а) подчиняется установленным правилам и дополнительных (избыточных) связей не обнаружено, то заданная система является геометрически неизменяемой и статически определимой (ГН СО ).

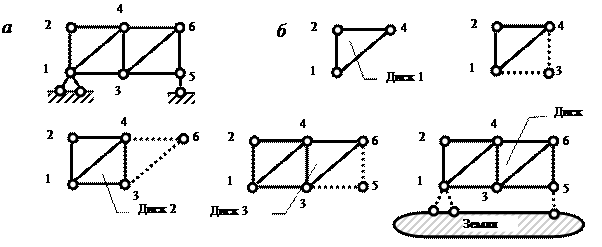
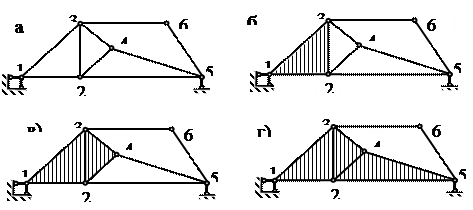
Пример 2. Кинематический анализ фермы (рис. 3.7, а).

Ферма собирается в такой последовательности:

1-й этап. Три стержня (1-2, 2-4, 1-4), как три диска, соединяются тремя шарнирами (1, 2, 4) согласно правилу 3.

2-й этап. К образовавшемуся Диску 1 (1-2-4) присоединяется узел 3 с помощью стержней 1-3 и 4-3 согласно правилу 1.

3-й этап. К образовавшемуся Диску 2 (1-2-4-3) присоединяется узел 6 с помощью стержней 4-6 и 3-6 согласно правилу 1.

4-й этап. К образовавшемуся Диску 3 присоединяется узел 5 с помощью стержней 3-5 и 6-5 согласно правилу 1.

5-й этап. Полученная ферма присоединяется к земле тремя опорными связями согласно правилу 2.

Поскольку образование фермы (рис. 3.7, а) подчиняется установленным правилам и дополнительных (избыточных) стержней не выявлено, то заданная система – геометрически неизменяемая и статически определимая (ГН СО ).

Ферма может быть собрана и в иной последовательности, но в любом случае вывод будет тем же.

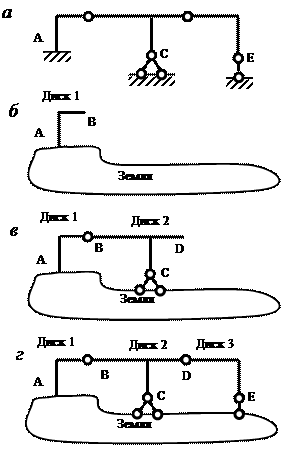
Пример 3. Кинематический анализ рамы (рис. 3.8, а).

Рама собирается в такой последовательности:

1-й этап. К земле прикрепляется стержень АВ (Диск 1 на рис. 3.8, б) с помощью жесткого защемления, которое эквивалентно трем связям (правило 2).

Рис.3.8. Последовательность сборки рамы

2-й этап. К образовавшейся системе «Земля + Диск 1» присоединяется диск 2 (стержень BCD) с помощью шарнира B и двух связей в точке С (рис. 3.8, в).

По правилу 2 достаточно в точке С иметь одну связь, поэтому вторая связь является избыточной.

3-й этап. К получившейся системе «Земля + Диск 1+ Диск 2» присоединяется диск 3 (стержень DE на рис. 2.8, г) с помощью шарнира D и опорного стержня в точке Е (правило 2).

Поскольку образование рамы (рис. 3.8, а) подчиняется установленным правилам и выявлена одна избыточная связь, то заданная система – геометрически неизменяемая и один раз статически неопределимая (ГН СН).

Пример 4. Кинематичес­кий анализ фермы (рис. 3.9, а).

Ферма собирается в такой последовательности.

1-й этап. Из трех стержней (1-2, 2-4, 1-4) образуется диск – треугольник 1-2-4 (правило 3), к которому прикрепляется узел 3 (правило 1) стержнями 1-3 и 4-3. Полученный диск 1-2-4-3 соединяется с землей тремя опорными связями (правило 2), образуя Диск 1 (рис. 3.9, б).

2-й этап. Три стержня (5-6, 6-7, 5-7) образуют по правилу 3 Диск 2 (рис. 3.9, в).

3-й этап. Диск 2 соединяется с Диском 1 тремя связями (4-6, 3-5, 7-8), но так как все эти связи пересекаются в одной точке 7, то правило 2 нарушается. Возможен взаимный поворот Диска 1 и Диска 2 относительно узла 7 на бесконечно малый угол.

Рис.3.9. Последовательность сборки фермы

Ввиду нарушения правила 2 заданная система является мгновенно изменяемой и не может служить расчетной схемой сооружения.

Пример 5. Найти степень свободы балки (см. рис. 3.6, а).

Пример 6. Найти степень свободы фермы (см. рис. 3.7, а).

Получаем W = 3·9 – 2·12 – 3 = 27 – 27 = 0.

При использовании формулы (2) имеем С = 9, У = 6, С_О = 3.

Получаем W = 2·6 – 9 – 3 = 12 – 12 =0.

Этот пример демонстрирует преимущество формулы (2) перед формулой (1). Признак ГН СО системы подтверждается в примере 2.

Пример 7. Найти степень свободы рамы (см. рис. 3.8, а).

W = 3·3 – 2·2 – 0 – 6 = –1, что является необходимым признаком ГН СН системы. Этот вывод подтверждается в примере 3.

Пример 8. Найти степень свободы фермы (см. рис. 3.9, а).

При использовании формулы (2) имеем С = 10, У = 7, С_О = 4.

Получаем W = 2·7 – 10 – 4 = 14 – 14 =0, что указывает на ГН СО систему. Однако анализ образования фермы (см. пример 4) приводит к выводу о мгновенной изменяемости системы. Этот пример демонстрирует недостаточность вычисления степени свободы системы по формуле для окончательного вывода о виде системы.

Пример 9. Кинематический анализ системы (рис. 3.10, а).

W = 3·3 – 2·0 – 5 – 4 = 9 – 9 = 0.

Система собирается в такой последователь­ности:

1-й этап. Диски Д2 и Д3 соединяются связями 3, 4, 5 по правилу 2 и образуют новый диск Д (рис. 3.10, б);

Рис.3.10. Схемы к примеру 9

Пример 10. Кинематический анализ системы (рис. 3.11).

W = 3·5 – 2·7 – 0 – 3 = 15 – 17 = –2.

Рис.3.11. Схема к примеру 10

W = 3·3 – 2·3 – 2 – 3 = 9 – 11 = –2.

Замечание: нельзя считать систему состоящей только из двух дисков (ломаных стержней ABC и ADC ), так как в этом случае стержни BE , CE , DE не соединяют диски между собой.

Система собирается в следующей последовательности:

1-й этап. Диски ABC и ADC соединяются в один диск двумя шарнирами А и С, т. е. четырьмя связями, одна их которых будет избыточной (правило 2).

2-й этап. К полученному диску присоединяется узел Е тремя связями, одна их которых будет избыточной (правило 1).

3-й этап. Собранный ди ск с дв умя избыточными связями прикрепляется к земле тремя опорными связями (правило 3).

Следовательно, заданная система – ГН СН (два раза).

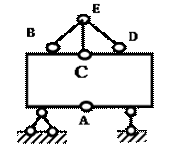
Пример 11. Произвести кинематический анализ системы (рис.3.12).

Определяем степень свободы системы по формуле П.Л.Чебышева :

где Д – число дисков, Ш – число простых шарниров, С₀ – количество стержней.

Рис.3.12. Схема к примеру 11

Отсюда W = 3 ∙ 5 – 2 ∙ 6 – 3 = 0, то есть система может быть геометрически неизменяемой и статически неопределимой. Чтобы убедиться, что это так, выполним анализ структуры системы. Так как диски АВ, ВС и АС связаны тремя шарнирами А , В и С, не лежащими на одной прямой, то они образуют диск, к которому жестко присоединен дискВД с помощью шарнира В и стержня СД, ось которого не проходит через центр шарнира. Эта неизменяемая фигура жестко присоединена к земле с помощью трех стержней, не пересекающихся в одной точке. Таким образом, система (рис.1.14) геометрически неизменяема и не является мгновенно изменяемой.

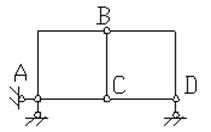
Пример 12. Выполнить кинематический анализ системы (рис.3.13).

Рис.3.13. Схема к примеру 12

Так как система является шарнирно-стержневой, то для определения ее степени свободы используем формулу (2):

где У – число узлов фермы; С – число внутренних стержней; С₀ – число опорных стержней.

Здесь У =6, С=8, С₀=3, следовательно, W = 2∙6 – 8 – 3 = 1.

Таким образом, система имеет одну степень свободы, и не может использоваться как строительная конструкция.

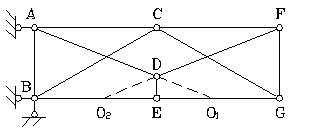
Пример 13. Исследовать ферму (рис.3.14).

Рис.3.14. Схема к примеру 13

По формуле (2) определяем степень свободы фермы: W = 2 ∙ 7 – 11 – 3 = 0, следовательно, система может быть геометрически изменяемой и статически определимой.

Проанализируем систему. Она состоит из трех дисков – треугольники АВС, CFG и стержень DЕ, связанных между собой стержнями ВЕ, АD, ЕG, DF, которые можно заменить фиктивными шарнирами О ₁ , О₂ и шарниром С. Следовательно, можно сделать вывод: все стержни соединены между собой жестко и прикрепляются к земле так же жестко с помощью трех стержней, не пересекающихся в одной точке.

Пример 14. Выполнить кинематический анализ системы (рис.3.15,а).

Рис.3.15. Схема к примеру 14

Пример 15. Произвести анализ образования системы, показанной на рис.3.16.

Рис.3.16. Схема к примеру 15

Пример 16. Произвести анализ образования системы, показанной на рис.3.17, а.

Рис.3.17. Схема к примеру 16

1. Пользуясь формулой (2) W = 2У – С – С ₀ для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У =6, число стержней системы С=9, число опорных стержней С₀=3, следовательно, W = 2 ∙ 6 – 9 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть неизменяемой и статически определимой.

2. Проводим анализ структуры системы. Рассмотрим треугольник 123, который в соответствии с третьим признаком является неизменяемой системой. Считая его жестким диском (заштрихован на рис. 3.17, б), присоединим к нему двумя стержнями (3-4 и 2-4) узел 4. Эти стержни не лежат на одной прямой, следовательно, на основании первого принципа узел 4 неподвижно прикреплен к диску 123. Полученная система также является жестким диском (заштрихован на рис.3.17, в ). Прикрепив к нему двумя стержнями (4-5 и 2-5) узел 5 снова получим жесткий диск, заштрихованный на рис.3.17, г). К этому диску присоединим двумя стержнями (3-6 и 5-6) не лежащими на одной прямой последний узел 6.

Поскольку система образована в соответствии с принципами образования структурно неизменяемых систем, она неизменяема и не является мгновенно изменяемой. К земле система прикреплена так же жестко, с помощью трех опорных стержней, не пересекающихся в одной точке.

Пример 17. Произвести кинематический анализ системы, показанной на рис. 3.18.

Рис.3.18. Схема к примеру 17

1. Пользуясь формулой W = 2У – С – С ₀ для шарнирно-стержневых систем определяем число степеней свободы. Поскольку, число узлов системы У =9, число стержней системы С=15, число опорных стержней С₀=3, следовательно, W = 2 ∙9 – 15 – 3 = 0, следовательно, система имеет необходимое количество связей, чтобы быть геометрически неизменяемой.

2. Проводим анализ структуры системы. Вначале найдем заведомо неизменяемые части системы – два диска, образованные треугольниками (заштрихованы на рис. 3.18, б). Они соединены тремя стержнями. Однако эти стержни пересекаются в одной точке (т. k на рис. 3.18, б). Следовательно, система мгновенно изменяемая.

Пример 18 . Проанализировать систему, изображенную на рис. 3.19.

Система состоит из четырех дисков ( A С, С E , EF и FH ) т.е. Д=4. Число шарниров Ш = 3 (все шарниры простые). Число опорных стержней С ₀ =2+1 ∙ 4=6. Степень свободы системы по формуле W = 3Д – 2Ш – С ₀ = 3 ∙ 4-2 ∙ 3-6=0.

Рис.3.19. Схема к примеру 18

Таким образом, рассматриваемая система неизменяема и не является мгновенно изменяемой.

Пример 19. Проверить геометрическую неизменяемость системы, приведенной на рис. 3.20.

Рис.3.20. Схема к примеру 19

Вместе с землей система состоит из трех дисков, соединенных между собой шарниром Ш_1–2 и четырьмя стержнями, эквивалентными условным шарнирам Ш_1–3 иШ_2–3.

Так как три шарнира, соединяющие три диска, лежат на одной прямой, система мгновенно изменяема.

3.3. Степень изменяемости системы

Системы не связанные с землей

Для системы, не связанной с землей, вместо степени свободы W вводится характеристика степень изменяемости V, которую вычисляют по формулам:

где смысл обозначений такой же, как в формулах (1) и (2).

Если V > 0, то система геометрически изменяемая.

Если V = 0, то система геометрически неизменяемая и статически определимая.

Условия геометрической неизменяемости V =0 и V примеры ниже).

Пример 20. Кинематический анализ системы (рис. 3.21).

При Д = 6, Ш = 9, С = 0 получаем

V = 3·6 – 2·9 – 0 – 3 = 18 – 21 = –3.

Рис.3.21. Схема к примеру 20

Пример 21. Кинематический анализ системы (рис. 3.22).

Рама имеет два замкнутых контура, а формула (3) не допускает наличия замкнутых контуров. Поэтому разделим раму четырьмя сечениями на три части (диска), соединенных между собой тремя связями в каждом из проведенных сечений.

Рис.3.22. Схема к примеру 21

Тогда получаем Д = 3, Ш = 0,

С = 3∙4 =12 и степень изменяемости

Анализируем порядок образования системы. К среднему диску прикрепляется левый диск с помощью шести связей, три из которых являются избыточными. Затем к образованному диску присоединяется правый диск с помощью шести связей, три из которых также избыточные.

Следовательно, анализируемая система геометрически неизменяемая и содержит шесть избыточных связей.

Источник