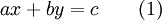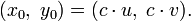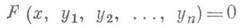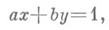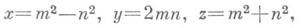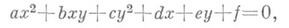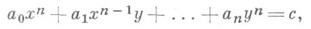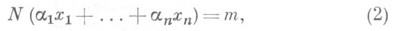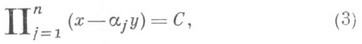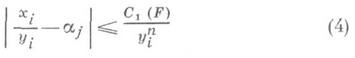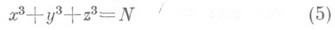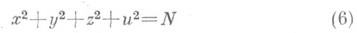что такое диофантовы уравнения

Диофантовы уравнения

Диофа́нтово уравнение или уравнение в целых числах — это уравнение с целыми коэффициентами и неизвестными, которые могут принимать только целые значения. Названы в честь древнегреческого математика Диофанта.

Содержание

Линейные диофантовы уравнения

Общий вид линейного диофантова уравнения: . В литературе под диофантовыми уравнениями иногда понимаются также уравнения более частного вида — с двумя неизвестными:

которые достаточно хорошо изучены.

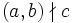
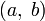
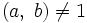
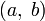
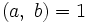
Если (то есть c не делится нацело на НОД), то уравнение (1) не разрешимо в целых числах. В самом деле, в этом случае , но тогда число, стоящее слева в (1) делится на , а стоящее справа — нет. Если в уравнении ax + by = 1 , то оно разрешимо в целых числах.

исходя из которого, можно положить

Некоторые другие уравнения

Неразрешимость в общем виде

Десятая проблема Гильберта, сформулированная в 1900 г., состоит в нахождении алгоритма решения произвольных диофантовых уравнений. В 1970 г. Юрий Матиясевич доказал алгоритмическую неразрешимость этой проблемы.

См. также

Полезное

Смотреть что такое «Диофантовы уравнения» в других словарях:

ДИОФАНТОВЫ УРАВНЕНИЯ — алгебраические уравнения или их системы с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или рациональные решения … Большой Энциклопедический словарь

ДИОФАНТОВЫ УРАВНЕНИЯ — алгебраич. уравнения или системы алгебраич. уравнений с рациональными коэффициентами, решения к рых отыскиваются в целых или рациональных числах. Обычно предполагается, что Д. у. имеют число неизвестных, превосходящее число уравнений, в связи с… … Математическая энциклопедия

Диофантовы уравнения — алгебраические уравнения или их системы с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или рациональные решения. * * * ДИОФАНТОВЫ УРАВНЕНИЯ ДИОФАНТОВЫ УРАВНЕНИЯ, алгебраические… … Энциклопедический словарь

Диофантовы уравнения — (по имени древнегреческого математика Диофанта) алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или… … Большая советская энциклопедия

ДИОФАНТОВЫ УРАВНЕНИЯ — алгебр. ур ния или их системы с целыми коэф., имеющие число неизвестных, превосходящее число ур ний, и у к рых разыскиваются целые или рациональные решения. Названы по имени Диофанта Александрийского … Естествознание. Энциклопедический словарь

ДИОФАНТОВЫ ПРОБЛЕМЫ АДДИТИВНОГО ТИПА — диофантовы уравнения, для к рых ставится задача нахождения целочисленных решений и к рые могут одновременно рассматриваться как аддитивные проблемы, т. е. как задачи о разбиении целого числа п(произвольного или подчиненного дополнительным… … Математическая энциклопедия

ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ — раздел теории чисел, в к ром изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов. Первоначальные задачи Д. п. касались рациональных приближений к действительным числам, но развитие теории привело к задачам, в … Математическая энциклопедия

УРАВНЕНИЯ — Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида… … Энциклопедия Кольера

Диофантовы приближения — часть теории чисел, изучающая приближения действительных чисел рациональными числами, или, при более широком понимании предмета, вопросы, связанные с решением в целых числах линейных и нелинейных неравенств или систем неравенств с… … Большая советская энциклопедия

Диофантово уравнение — это уравнение вида где P целочисленная функция (например, полином с целыми коэффициентами), а переменные принимают целые значения. Названы в честь древнегреческого математика Диофанта. Содержание 1 Примеры … Википедия

Источник

Алгебра. 7 класс

Линейные диофантовы уравнения

Значения коэффициентов и неизвестных

Выражение одной переменной через другую

Неразрешимые диофантовы уравнения

Решение линейных диофантовых уравнений

Решение линейных диофантовых уравнений

Необходимо запомнить

Диофантово уравнение – это уравнение решение которого ищется в целых (в некоторых задачах в натуральных) числах.

Расширенный алгоритм Евклида

Разделим большее из этих чисел на меньшее, то есть 24 на 17.

Получаем 24 : 17 = 1 (ост. 7), что можно записать в виде равенства:

Теперь разделим делитель на остаток, то есть 17 на 7, получим:

Снова разделим делитель на остаток:

Выполним деление еще раз:

Мы получили остаток, равный нулю, так как 3 делится на 1 без остатка.

Теперь выполним действия «в обратном направлении», то есть выразим 18 (остаток) через числа 612 и 342.

Для этого в каждой строчке последовательности Евклида выразим остатки через делимое и делитель (второй столбик таблицы):

Получаем, 18 = 72 – 54 ∙ 1 = 72 – (270 – 72 ∙ 3) = 342 – 270 ∙ 1 – (270 – (342 – 270 ∙ 1) ∙ 3) =

342 – ((612 – 342 ∙ 1) ∙ 1) – (612 – 342 ∙ 1 – (342 – (612 – 342 ∙ 1)) ∙ 3) = 342 – 612 + 342 – 612 + 342 + 342 ∙ 3 – 612 ∙ 3 + 342 ∙ 3= 342 ∙ 9 – 612 ∙ 5 = 342 ∙ 9 + 612 ∙ (-5).

Найдем при помощи алгоритма Евклида НОД(24, 17):

Выполним действия «в обратном направлении»:

1 = 7 – 3 · 2 = 7 − (17 – 7 · 2) · 2 = 7 – 17 · 2 + 7 · 4 + 5 · 7 – 2 · 17 = 5 · (24 – 17 · 1) – 2 · 17 = 5 · 24 – 5 · 17 – 2 · 17 = 5 · 24 – 7 · 17 = 24 · 5 – 17 · 7.

В исходном уравнении в правой части стоит число 2. Поэтому умножим обе части уравнения на 2. Получим:

То есть, x 0 = 10, y 0 = 14 – частные решения уравнения 24x −17y = 2.

Если уравнение имеет одно решение в целых числах, то оно имеет бесконечное множество других решений.

Прибавим коэффициент b к значению х.

Чтобы значение исходного уравнения не изменилось, при прибавлении одного числа к х нужно вычесть другое число из у :

Ответ: ( 10 − 17t,14 − 24t ), t ∈ Z.

Источник

ДИОФАНТОВЫ УРАВНЕНИЯ

— алгебраич. уравнения или системы алгебраич. уравнений с рациональными коэффициентами, решения к-рых отыскиваются в целых или рациональных числах. Обычно предполагается, что Д. у. имеют число неизвестных, превосходящее число уравнений, в связи с чем они наз. также неопределенными уравнениями. Понятие Д. у. в современной математике часто относят также к алгебраич. уравнениям, решения к-рых отыскиваются среди целых алгебраич. чисел какого-либо алгебраич. расширения поля рациональных чисел Q, среди р-адических чисел и т. п.

Исследование Д. у. относится к области пограничной между теорией чисел и алгебраич. геометрией (см. Диофантова геометрия).

Исследование Д. у. обычно связано с большими трудностями. Более того, можно явно указать многочлен

с целыми коэффициентами такой, что не существует алгоритма, позволяющего по любому целому хузнавать, разрешимо ли уравнение

Целые положительные решения этого уравнения представляют длины катетов х, у и гипотенузы z прямоугольных треугольников с целочисленными длинами сторон и наз. пифагоровыми числами. Все тройки взаимно простых пифагоровых чисел можно получить по формулам:

где ти п— целые взаимно простые числа (m>n>0). Диофант в соч. «Арифметика» занимался разысканием рациональных (не обязательно целых) решений специальных видов Д. у. Общая теория решения Д. у. 1-й степени была создана в 17 в. К. Г. Баше (С. G. Bachet); о решении систем Д. у. 1-й степени подробнее см. в статье Линейное уравнение. К началу 19 в. трудами П. Ферма (P. Fermat), Дж. Валлиса (J. Wallis), Л. Эйлера (L. Euler), Ж. Лагранжа (J. Lagrange) и К. Гаусса (С. Gauss) в основном было исследовано Д. у. вида

где а, b, с, d, e, f— целые числа, т. е. общее неоднородное уравнение 2-й степени с двумя неизвестными. С помощью цепных дробей Ж. Лагранж исследовал общее неоднородное Д. у. 2-й степени с двумя неизвестными. К. Гаусс построил общую теорию квадратичных форм, являющуюся основой решения нек-рых типов

В исследованиях Д. у. выше 2-й степени с двумя неизвестными серьезные успехи достигнуты лишь в 20 в. А. Туэ (А. Т1ше) установил, что Д. у.

Исследование целых решений уравнения (1) является естественным обобщением задачи о пифагоровых тройках. Положительное решение проблемы Ферма для n=4 получено Л. Эйлером. Благодаря этому результату проблема Ферма сводится к доказательству отсутствия ненулевых целых решений уравнения (1) при нечетном простом п. Полное исследование решений уравнения (1) не завершено (1978). Трудности, возникающие при его решении, связаны с отсутствием единственности разложения на простые множители в кольце целых алгебраич. чисел. Теория дивизоров в кольцах целых алгебраич. чисел дает возможность установить справедливость теоремы Ферма для многих классов простых показателей п.

Арифметика колец целых алгебраич. чисел используется также в ряде других задач Д. у. Так. напр., ее методами подробно исследованы уравнения вида

где F(x, у)- неприводимый однородный многочлен степени . Это уравнение может быть записано в виде

где a_i— все корни многочлена F(z,l) = 0. Существование бесконечной последовательности целых решений уравнения (3) привело бы к соотношениям вида

для какого-либо a_j. Без ограничения общности можно считать, что Поэтому при достаточно большом i неравенство (4) будет противоречить Туэ— Зигеля— Рота теореме, откуда следует, что уравнение F(x, y)=С, где F- неприводимая форма степени, большей или равной 3, не может иметь бесконечного числа решений.

Уравнения вида (2) представляют собой достаточно узкий класс среди всех Д. у. Напр., несмотря на простой вид, уравнения

не входят в этот класс. Исследование решений второго из приведенных уравнений относится к сравнительно хорошо изученному разделу Д. у.- представлению чисел квадратичными формами. Теорема Лагранжа утверждает разрешимость уравнения (6) при всяком натуральном N. Суммой трех квадратов представляется любое натуральное число, отличное от чисел вида 4 a (8k-1), где аи к,- целые неотрицательные (теорема Гаусса). Известны критерии существования рациональных или целых решений уравнений вида

где a_ij и b рациональны, допускает рациональное решение тогда и только тогда, когда оно разрешимо в действительных числах, а также в р-адических числах для каждого простого числа р.

Представление чисел произвольными формами 3-й степени и формами более высоких степеней изучено меньше нз-за возникающих здесь часто принципиальных трудностей. Одним из основных методов исследования представления чисел формами высших степеней является тригонометрических сумм метод. Этот метод состоит в явной записи через интеграл Фурье числа решений уравнения, затем с помощью кругового метода осуществляется, в сущности, выражение числа решений уравнения через число решений соответствующих сравнений. Метод тригонометрических сумм меньше, чем другие методы, зависит от алгебраической специфики уравнения.

Существует большое число конкретных Д. у., решаемых элементарными методами (см. [5]).

Лит.:[1] Виноградов И. М., Основы теории чисел, 8 изд., М., 1972; [2] Боревич З.

Источник

Для чего используются диофантовы уравнения и могут ли в них быть отрицательные корни?

Прежде всего, диофантовы уравнения интересны сами по себе. Например, Великая теорема Ферма, одна из самых популярных теорем математики, представляет из себя диофантово уравнение. Обычно рассматриваются уравнения с положительными корнями, но и отрицательные корни также входят в область определения.

Часто такое встречается в молекулярной физике и органической химии при поиске оптимальных структур. Даже подбор коэффициентов в химических уравнениях иногда превращается в решение систем диофантовых уравнений.

Также такие уравнения используются в различных компьютерных алгоритмах. Например, при расшифровке алгоритма RSA, который используется во многих системах цифровой подписи и шифрования. Похожие случаи, связанные с решением диофантовых уравнений, возникают в алгоритмах обработки видео, проектирования осветительных систем (для расчета стробоскопических эффектов) и разработке систем управления сложными машинами (например, вертолетами).

Уравнения такого типа иногда встречаются в экономике и теории вероятностей. Чаще всего это линейные диофантовы уравнения. Их связь с реальной жизнью можно легко показать на пальцах: допустим, у кого-то есть 1000 рублей и он хочет купить карандашей по 40 рублей и ручек по 35 рублей. Сколькими способами можно это сделать? (подсказка: 3)

Стоит упомянуть одно интересное историческое приложение, использующее свойства диофантовых уравнений. Согласно некоторым источникам, китайские военачальники, чтобы узнать численность своей армии, давали несколько последовательных команд «В колонну по 7 становись!», «В колонну по 11 становись!», «В колонну по 13 становись!», «В колонну по 17 становись!» и в каждом случае выясняли, сколько солдат получилось в последнем ряду. После этого (только по полученным остаткам!) вычислялось общее количество солдат.

Источник

Диофантовы уравнения

Полезное

Смотреть что такое «Диофантовы уравнения» в других словарях:

ДИОФАНТОВЫ УРАВНЕНИЯ — алгебраические уравнения или их системы с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или рациональные решения … Большой Энциклопедический словарь

ДИОФАНТОВЫ УРАВНЕНИЯ — алгебраич. уравнения или системы алгебраич. уравнений с рациональными коэффициентами, решения к рых отыскиваются в целых или рациональных числах. Обычно предполагается, что Д. у. имеют число неизвестных, превосходящее число уравнений, в связи с… … Математическая энциклопедия

Диофантовы уравнения — Диофантово уравнение или уравнение в целых числах это уравнение с целыми коэффициентами и неизвестными, которые могут принимать только целые значения. Названы в честь древнегреческого математика Диофанта. Содержание 1 Линейные диофантовы… … Википедия

Диофантовы уравнения — алгебраические уравнения или их системы с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или рациональные решения. * * * ДИОФАНТОВЫ УРАВНЕНИЯ ДИОФАНТОВЫ УРАВНЕНИЯ, алгебраические… … Энциклопедический словарь

ДИОФАНТОВЫ УРАВНЕНИЯ — алгебр. ур ния или их системы с целыми коэф., имеющие число неизвестных, превосходящее число ур ний, и у к рых разыскиваются целые или рациональные решения. Названы по имени Диофанта Александрийского … Естествознание. Энциклопедический словарь

ДИОФАНТОВЫ ПРОБЛЕМЫ АДДИТИВНОГО ТИПА — диофантовы уравнения, для к рых ставится задача нахождения целочисленных решений и к рые могут одновременно рассматриваться как аддитивные проблемы, т. е. как задачи о разбиении целого числа п(произвольного или подчиненного дополнительным… … Математическая энциклопедия

ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ — раздел теории чисел, в к ром изучаются приближения нуля значениями функций от конечного числа целочисленных аргументов. Первоначальные задачи Д. п. касались рациональных приближений к действительным числам, но развитие теории привело к задачам, в … Математическая энциклопедия

УРАВНЕНИЯ — Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида… … Энциклопедия Кольера

Диофантовы приближения — часть теории чисел, изучающая приближения действительных чисел рациональными числами, или, при более широком понимании предмета, вопросы, связанные с решением в целых числах линейных и нелинейных неравенств или систем неравенств с… … Большая советская энциклопедия

Диофантово уравнение — это уравнение вида где P целочисленная функция (например, полином с целыми коэффициентами), а переменные принимают целые значения. Названы в честь древнегреческого математика Диофанта. Содержание 1 Примеры … Википедия

Источник