что такое динамическое приложение

Динамическое программирование примеры

В информатике есть несколько способов описания подхода к решению алгоритма. Жадный, наивный, разделяй и властвуй — всё это способы решения алгоритмов. Один из таких способов называется динамическим программированием (DP). В этой статье мы рассмотрим, что такое динамическое программирование, его характеристики и два основных подхода к решению алгоритмов с помощью DP.

Что такое динамическое программирование?

Концепция динамического программирования была создана, чтобы помочь повысить эффективность методов решения алгоритмов грубой силой или «разделяй и властвуй».

Скажем, например, у нас есть рюкзак, в который может поместиться только определённое количество предметов. Какая комбинация предметов даст нам максимальную ценность? Или предположим, что у нас есть рюкзак определённой грузоподъёмности. Какая комбинация предметов с заданным весом даст нам максимальную ценность?

Наивные решения

Наивное решение — это первое, что приходит в голову программисту. Он может быть не самым эффективным и не использовать преимущества некоторых концепций. Тем не менее, это простое решение, которое решает проблему. Как начинающий программист, в ваших интересах сначала придумать наивные решения, а потом провести рефакторинг для их оптимизации.

Нисходящие решения

Это первый способ использования динамического программирования в вашем решении. Нисходящее решение возьмёт наивное решение, использующее рекурсию, а затем добавит метод, называемый мемоизацией, для его оптимизации. Мемоизация действует как своего рода кеш для хранения наших подзадач по мере продвижения, чтобы алгоритм работал быстрее. Обычно это происходит в форме объекта или словаря.

Решения снизу-вверх

Другой тип решения динамического программирования, который избегает рекурсии и табулирования с самого начала, называется восходящим решением. Это отличный способ, если вы хотите избежать использования большого объёма памяти или предотвратить случайное переполнение стека.

Фибоначчи

Последовательность Фибоначчи — это последовательность чисел, каждое из которых представляет собой сумму двух предыдущих чисел, начиная с 0 и 1:

Fn = 0, 1, 1, 2, 3, 5, 8, 13, 21…и т.д.
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34…и т.д.

Подсказка

По заданному числу n найдите n- е число в последовательности Фибоначчи.

Решение 1. Наивно

Наивное решение — это решение, которое программист может придумать, впервые взглянув на проблему. Помните, что наивность необязательно означает плохо. Наивное решение обычно означает, что проблему можно решить с помощью других методов, которые могут создать более оптимальное или эффективное решение. Наивное решение — это хорошо, потому что оно означает, что вы на правильном пути.

Пример наивного решения для Фибоначчи выглядит так:

const fibNaive = (num) => <
if(num <
if(num Читайте также: Что такое IDE и какая лучше

Базовый вариант здесь почти такой же. Разница в том, что мы начинаем с памятки по умолчанию, в которой есть наши первые два числа Фибоначчи. Это вместо того, чтобы просто возвращать переданное число. Мы присваиваем переменный результат нашему уравнению Фибоначчи, которое мы использовали при возврате наивного решения.

В операторе if мы проверяем, существует ли ключ в memo — если нет, мы добавляем его. Возвращаем результат так же, как и в наивном решении.

В конечном счёте, у этого решения есть два отличия. Во-первых, мы добавили memo объект, который запоминает то, что мы уже выяснили. И во-вторых, мы добавили условие, которое проверяет, существует ли эта пара ключ: значение в memo объекте. Если нет, то добавляет.

Это решение изменяет временную сложность с O (2 n) на O (n).

Решение 3. Подход к динамическому программированию № 2 — снизу-вверх с табуляцией

Эта версия решения использует итерацию для решения проблемы и выводит результат в таблицу по мере продвижения. Мы начинаем с объекта JavaScript (или здесь вполне приемлем массив), который будет хранить наши значения. Мы используем эти значения, чтобы довести до нашего числа nth.

for(let i = 3; i <
//find all the substrings.
substrs = [];
maxString = «»;
otherString = «»;
if(str1.length > str2.length) <
maxString = str1;
otherString = str2;
> else <
maxString = str2;
otherString = str1;
>

for(let i = 0; i < // O(m)
if(new RegExp(string).test(otherString)) <
if(maxLength <

let i = str1.length;
let j = str2.length;
//if the strings don’t exist, return 0
if(i === 0 || j === 0) <
return count;
>

if(str1[i — 1] === str2[j — 1]) < // if the chars are the same, up the count and shorten string by 1
count = topDown(str1.slice(0, i — 1), str2.slice(0, j — 1), count + 1);
>
count = Math.max(count, //max between count and the other function
Math.max( // max between looking at shortening one word vs shortening the other word.
topDown(str1.slice(0, i), str2.slice(0, j — 1), 0),
topDown(str1.slice(0, i — 1), str2.slice(0, j), 0)));

Сложность по времени для этого решения составляет O (n + m), чтобы учесть размеры различных строк.

Решение 3. Восходящее решение с табуляцией

Третье решение этой проблемы предполагает использование восходящего подхода. В этом подходе вы должны создать двумерный массив / матрицу, которая будет табулировать максимальную длину подстроки. Первое, что нужно сделать, это создать пустую матрицу, используя длины строк.

for (let i = 0; i <
let table = create2DArray(A, B); // create the table
let max = 0; // initialize and declare max substring length to be 0
//start i and j at 1 so we can compare characters to previous row and column
for (let i = 1; i

Источник

Что такое динамическое программирование — объясняют эксперты

Авторизуйтесь

Что такое динамическое программирование — объясняют эксперты

Время от времени в разных статьях упоминается динамическое программирование, которое начинающий программист может спутать с чем-нибудь вроде объектно-ориентированного программирования. Мы попросили экспертов простым языком объяснить, что такое динамическое программирование.

технический директор iD EAST

Динамическое программирование — достаточно широко используемый подход к решению задач, основанный на идее «разделяй и властвуй». Достаточно часто невозможно или крайне затруднительно создать некий общий алгоритм решения проблемы, который бы брал входные данные, что-то с ними делал и сразу выдавал ответ.

Часто способа решить задачу методом «делай раз, делай два, делай три» не существует. Но всегда можно разделить большую задачу на множество маленьких и дробить так до тех пор, пока упрощённые задачи не станут примитивно простыми. Это подход, известный как «разделяй и властвуй». Довольно часто для этого используется рекурсия — вызов функцией самой себя.

Важная особенность чтобы этот процесс не зациклился нужно чтобы на каком-то этапе задача сводилась к примитивному случаю, ответ на который известен сразу. Пример — вычисление факториала числа. Такую задачу можно решить и с помощью простого алгоритма n!=1·2·3·…·n, в этом случае можно сразу получить значение (например 4! = 1·2·3·4 = 24, а 5! = 1·2·3·4·5 = 120). Но эту же задачу можно решить и рекурсивно, ведь 5! = 5·4!, а 4! = 4·3! и так далее. Значит можно написать простую функцию расчета факториала n!, которая будет умножать число на результат вызова самой себя для более простого случая (n-1)!. И только в примитивном случае 1! функция вызывать саму себя не будет, а сразу вернёт 1, это важный момент, чтобы не возникло зацикливания.

Но «разделяй и властвуй» — это ещё не совсем динамическое программирование, так как такой подход хоть и прост, но часто приводит к лавинообразному росту необходимых вычислений, хоть сам метод может быть сколь угодно простым.

Взять, к примеру, задачу поиска кратчайшего маршрута по городу из точки А в точку Б. На практике такие задачи решаются с использованием теории графов, когда каждой улице в городе ставится в соответствие ребро графа, а каждой возможной точке пребывания — узел графа. Каждому ребру приписывается некоторая условная «стоимость», соответствующая, например времени прохождения или даже непосредственно денежная стоимости проезда по соответствующей «улице». Эта стоимость в реальности может даже меняться с течением времени, например из-за пробок. Тогда необходима функция, находящая кратчайший маршрут — такую последовательность узлов, пройдя через которые мы получим минимальную «стоимость» прохождения всех соединяющих их рёбер.

И вот для таких задач методы динамического программирования становится практически единственными рабочими вариантами решения. Методы рекурсии здесь уже не подойдут: можно, конечно, решить эту задачу и таким образом: написать функцию, возвращающую стоимость ухода из точки А по каждой из возможных «улиц», каждая из этих функций в свою очередь добавит к ней стоимость участка до следующего «перекрёстка», вызвав саму себя еще раз, и повторит это многократно, пока в результате не «дойдёт» до точки Б. По итогу, среди всех цепочек ответов можно будет выбрать ту, стоимость которой минимальна и получить ответ на задачу. Но на практике сделать такое возможно только для очень простых графов с десятками узлов, например для карты метро. А вот уже в масштабах карты улиц города подобные алгоритмы становятся нереалистичными.

тимлид в ADCI Solutions

Если вкратце, то динамическое программирование — это способ решить задачу, разбив её на мелкие задачи и скомбинировав их решения.

Обычно динамическое программирование применяют в задачах, связанных с оптимизацией, например, когда нужно найти кратчайший маршрут для перемещения из города A в город B. Либо это могут быть задачи, где нужно просчитать все возможные комбинации переходов или расположения элементов. Классический пример, в котором используется этот метод — последовательность чисел Фибоначчи.

Как видно, для решения задачек с последовательностями, нужно определить следующие условия: рекуррентная зависимость элементов последовательности друг от друга, начальное состояние. Они не всегда могут быть заданы в условии напрямую, как это было в задаче выше. Например, в видео «Динамическое программирование: траектории кузнечика» разбирают задание с количеством переходов из точки A в B.

В рассмотренных выше случаях параметром состояния было одно число, однако существуют и более сложные, многомерные классы задач. Для многомерной динамики параметрами состояния могут быть:

Поиск оптимального состояния динамики, переходов и порядка пересчёта (прямой или обратный) и включает в себя метод динамического программирования.

Узнать подробности о применениях этого метода и способах его оптимизации можно почти во всех в книжках по алгоритмам, например, в книге «Алгоритмы. Построение и анализ».

начальник отдела разработки прикладного ПО в компании ИВК

В теории вычислительных систем под термином «динамическое программирование» понимается способ решения сложных задач путём разбиения их на более простые подзадачи. Динамическое программирование применимо не ко всем задачам, а лишь к тем, которые обладают «оптимальной структурой». Оптимальная структура означает, что задача может быть разбита на несколько аналогичных задач меньшего размера, при этом для решения конечной задачи могут быть использованы результаты решения меньших задач. Примеры задач с оптимальной структурой — вычисление факториала числа, построение ряда чисел Фибоначчи, вычисление расстояния Левенштейна (красивое название, скрывающееся внутри всем известной задачи diff, вычисляющей разницу между двумя текстовыми файлами). Программист, не знакомый с теорией вычислительных систем, может подумать, здесь кроется какая-то сложная математика, но на самом деле речь идёт о всем хорошо знакомом подходе — рекурсии. Все знают, как вычислить факториал числа: нужно умножить это число на факториал числа, меньшего на единицу: F(n) = n*F(n-1) (для краткости опущена проверка n >= 1) — просто и изящно.

Так вот, динамическое программирование — это рекурсия с сохранением результатов вычислений. Представим, что нам постоянно нужно вычислять факториал разных чисел. Каждый раз, когда нам нужно вычислить факториал, например, числа 5, нам необходимо произвести 4 умножения — 5*4*3*2*1. А что, если сохранить промежуточные результаты? Допустим, мы когда-то раньше вычислили 4! = 24. Значит, нам нужно проделать только одно умножение — 5*24. А в следующий раз, когда нас спросят 5!, мы вообще можем вернуть результат сразу же. Понятно, что при таком подходе растёт скорость вычислений, но и возрастает потребление памяти. Что важнее — скорость или память — вечный вопрос. Принимать решение нужно исходя из конкретных условий.

руководитель отдела программных разработок и поддержки компании «ГЭНДАЛЬФ»

Динамическое программирование – это метод, который позволяет эффективно решать многие задачи, прежде всего, задачи комбинаторной оптимизации.

Суть метода в следующем: имеющуюся задачу рекурсивно разбиваем на более маленькие подзадачи, их — на ещё меньшие и так далее. Но решаем задачи в обратном порядке: сначала маленькие (запоминаем их решение), потом переходим к задачам побольше (строим их решение на основе сохранённых решений маленьких задач) и так далее, пока не решим исходную большую задачу.

Недостаток: обычно требуется много памяти для хранения промежуточных результатов.

Lead Software Engineer в EPAM

Вычислительная сложность многих задач не зависит от входных параметров, например, получение элемента по индексу в массиве не зависит от длины массива и всегда выполняется за константное время. В то же время есть задачи, для которых время выполнения линейно зависит от значения параметров, например, получение элемента по индексу в связанном списке ― чем больше элементов, тем больше времени потребуется на поиск нужного элемента. Естественно, существуют и задачи, для которых использование полного перебора требует слишком много времени, например, поиск кратчайшего маршрута между двумя городами в случае полного перебора потребует построение n! вариантов, что при больших n неэффективно.

Некоторые подобные задачи можно решить путем разбиения исходной задачи на подзадачи меньшего размера и сложности, решив которые и объединив результаты, можно получить решение исходной задачи. Такой подход называется динамическим программированием и был предложен Ричардом Беллманом в 1940-х годах.

Динамическое программирование придерживается двух подходов к решению задач:

Одной из самых известных задач динамического программирования является задача вычисления чисел Фибоначчи, и она эффективно решается методом восходящего динамического программирования. При использовании этого подхода для нахождения N-го элемента в последовательности происходит последовательное нахождение первого, второго и последующих элементов как суммы двух предыдущих. Данный подход имеет сложность O(N), в то время как использование классического рекурсивного подхода имеет приблизительную сложность O(2^N), что существенно больше.

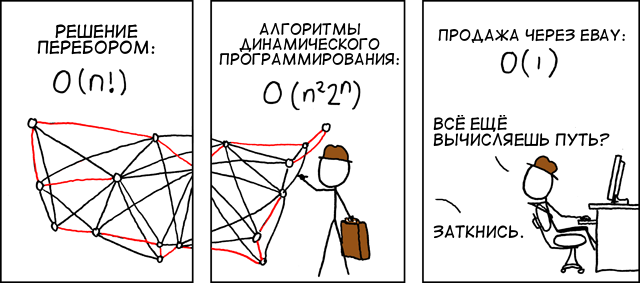
С помощью чисел Фибоначчи описываются многие явления, однако, давайте посмотрим на более практический пример ― задачу коммивояжера или, на современный лад, курьера ― курьер должен посетить N адресов, побывав на каждом из адресов ровно по одному разу и завершить свой маршрут в исходной точке. Задача заключается в нахождении маршрута минимальной длинны.

Данную задачу можно решить методом полного перебора ― сгенерировать все возможные маршруты (всего их N!) для N адресов, а затем выбрать маршрут минимальной длины. Сложность данного алгоритма O(N! * N) и время вычисления очень быстро растет при росте количества адресов ― если для трех адресов нужно рассмотреть шесть вариантов, то для 10 уже около четырех миллионов!

Использование подходов динамического программирования может не дать наилучшего решения, но, тем не менее, оно будет достаточно хорошим и за приемлемое время. Суть подхода к решению данной задачи заключается в поиске ближайшего адреса на каждом шаге ― из исходной точки, затем следующего ближайшего пункта назначения из первого адреса и так далее. Полученное решение не будет идеальным, но потребует гораздо меньше времени ― O(N^2 * 2^N), что для тех же 10 адресов 1124 вычислений.

Таким образом, мы рассмотрели основную идею динамического программирования ― разбиение сложной задачи на коллекцию более простых, которые суммарно можно решить за гораздо меньшее время.

Источник

Учебник по динамическому программированию: создание эффективных программ на Python

Если вы изучаете Python, может быть сложно сделать этот шаг от написания образца кода до эффективного кода. По мере того, как вы набираете навыки, эффективность времени выполнения программы становится все более важной, выступая в качестве ключевого показателя успеха при собеседовании по кодированию, а затем и в реальных решениях.

Один из способов повысить эффективность ваших рекурсивных программ — начать использовать динамическое программирование, экономящую время технику на основе хранения, вместо рекурсии грубой силы. В динамическом программировании используется принцип оптимальности, который заключается в том, что если все шаги процесса оптимизированы, то оптимизируется и результат. В нашем случае оптимальный шаг — это тот, который занимает наименьшее количество времени, что в программировании означает наименьшее количество новых вычислений.

Чтобы помочь вам перейти к эффективному коду Python, вот краткое руководство о том, что такое динамическое программирование, почему оно более эффективно и как использовать его для решения распространенных задач собеседования.

Что такое динамическое программирование?

Динамическое программирование — это метод решения сложных проблем путем рекурсивного разбиения их на подзадачи, каждая из которых затем решается индивидуально. Динамическое программирование оптимизирует рекурсивное программирование и экономит время на повторное вычисление входных данных позже.

Это отличается от техники » Разделяй и властвуй» тем, что подзадачи в решениях динамического программирования перекрываются, поэтому некоторые из одинаковых шагов, необходимых для решения одной подзадачи, также необходимы для других подзадач.

Это подводит нас к главному преимуществу динамического программирования. Вместо того, чтобы пересчитывать эти общие шаги, динамическое программирование позволяет нам просто сохранять результаты каждого шага в первый раз и повторно использовать их каждый раз.

Примечание: динамическое программирование является частным случаем более широкой категории рекурсивного программирования, однако не во всех рекурсивных случаях можно использовать динамическое программирование.

Почему динамическое программирование эффективно? Рекурсия против DP

Если они так тесно переплетены, почему динамическое программирование отдается предпочтению, когда это возможно? Это связано с тем, что рекурсивные программы грубой силы часто повторяют работу, когда сталкиваются с перекрывающимися шагами, тратя ненужное время и ресурсы в процессе.

Динамическое программирование решает эту проблему, гарантируя, что каждый идентичный шаг выполняется только один раз, и сохраняя результаты этого шага в сборщике, таком как хеш-таблица или массив, для вызова всякий раз, когда это понадобится снова. При этом динамическое программирование позволяет сократить повторяемость работы и, следовательно, повысить эффективность выполнения.

Примечание. В динамическом программировании эффективность использования пространства существенно снижается, поскольку для хранения решений требуется пространство, не используемое в рекурсивных решениях методом грубой силы.

Примеры динамического программирования

Динамическое программирование в реальном мире

В отличие от компьютеров, процессы, основанные на памяти, такие как динамическое программирование, интуитивно понятны людям. Рассмотрим этот пример из реальной жизни:

Представьте, что вы хотите пойти в новый продуктовый магазин через несколько улиц, но не знаете, как туда добраться. Чтобы решить подзадачу маршрута к магазину, вы просматриваете маршруты на карте вашего смартфона, а затем направляетесь туда.

Если бы вы думали рекурсивно, каждый раз, когда вы хотели пойти в магазин, вам нужно было бы найти время, чтобы еще раз просмотреть направления.

Вместо этого мы, естественно, думаем динамично, запоминая направления к магазину с того момента, как мы их впервые искали, и в результате нам не нужно тратить время на их поиск, когда мы пойдем в будущее.

По сути, это то, как динамическое программирование работает и в программах.

Факторная проблема

Мы можем увидеть в реальной жизни, насколько динамическое программирование более эффективно, чем рекурсия, но давайте посмотрим, как это работает с кодом Python!

Ниже у нас есть два решения, которые находят число Фибоначчи для заданного входа, а затем показывают график времени выполнения программы. Левая вкладка представляет собой простую рекурсию грубой силы, а правая вместо этого использует динамическое программирование.

Посмотрите на разницу.

Recursion

Вы не должны изменять подпись данной функции; однако вы можете создать новую функцию с другой подписью и вызвать ее из предоставленной функции.

Попробуйте придумать простое решение этой проблемы. После того, как вы это реализовали, добавьте мемоизацию, чтобы учесть более сложные проблемы.

Примеры входных данных:

В этой задаче немного сложно увидеть перекрывающиеся проблемы, поскольку они не следуют определенному шаблону. Но если вы присмотритесь, вы заметите, что емкость и индексный кортеж часто повторяются. На все эти подзадачи есть одинаковые ответы. Посмотрите на следующую визуализацию.

Как видно из визуализации, мы можем мемоизировать на основе кортежа емкости и индекса. Это единственное дополнение в этом коде по сравнению с предыдущим с простой рекурсией. Перед рекурсивным шагом мы проверяем, доступен ли нам результат в таблице заметок. Точно так же после оценки результата мы снова сохраняем его в таблице заметок.

Проблема с разменом монет

Это вариант «проблемы размены монет», который часто задают на собеседованиях по кодированию.

Имея список денежных купюр, вам необходимо подсчитать количество способов, которыми вы можете представить определенную сумму. Например, если у вас есть только два вида счетов, 10 и 20 долларов, и вы хотите представить 30 долларов, есть только два способа:

При разработке алгоритма будьте особенно осторожны, чтобы не переоценить. 30 долларов могут быть представлены как 20 + 10 долларов, а также 10 + 20 долларов, но это одно и то же. Следовательно, не стоит рассчитывать оба случая.

Простое рекурсивное решение приведет к тайм-ауту для больших входных данных; таким образом, вы должны попытаться написать алгоритм динамического программирования. Начните с рекурсивного решения и создайте динамическое решение.

Источник

Динамическое программирование для начинающих

Авторизуйтесь

Динамическое программирование для начинающих

Динамическое программирование — тема, которой в рунете посвящено довольно мало статей, поэтому мы решили ею заняться. В этой статье будут разобраны классические задачи на последовательности, одномерную и двумерную динамику, будет дано обоснование решениям и описаны разные подходы к их реализации. Весь приведённый в статье код написан на Java.

О чём вообще речь? Что такое динамическое программирование?

Хорошо, как это использовать?

Решение задачи динамическим программированием должно содержать следующее:

И что, мне для решения рекурсивный метод писать надо? Я слышал, они медленные.

Конечно, не надо, есть и другие подходы к реализации динамики. Разберём их на примере следующей задачи:

Идея решения

Здесь нам даны и начальные состояния (a₀ = a₁ = 1), и зависимости. Единственная сложность, которая может возникнуть — понимание того, что 2n — условие чётности числа, а 2n+1 — нечётности. Иными словами, нам нужно проверять, чётно ли число, и считать его в зависимости от этого по разным формулам.

Рекурсивное решение

Очевидная реализация состоит в написании следующего метода:

Рекурсивное решение с кэшированием значений

Идея мемоизации очень проста — единожды вычисляя значение, мы заносим его в какую-то структуру данных. Перед каждым вычислением мы проверяем, есть ли вычисляемое значение в этой структуре, и если есть, используем его. В качестве структуры данных можно использовать массив, заполненный флаговыми значениями. Если значение элемента по индексу N равно значению флага, значит, мы его ещё не вычисляли. Это создаёт определённые трудности, т.к. значение флага не должно принадлежать множеству значений функции, которое не всегда очевидно. Лично я предпочитаю использовать хэш-таблицу — все действия в ней выполняются за O(1), что очень удобно. Однако, при большом количестве значений два числа могут иметь одинаковый хэш, что, естественно, порождает проблемы. В таком случае стоит использовать, например, красно-чёрное дерево.

Для уже написанной функции f(int) кэширование значений будет выглядеть следующим образом:

Не слишком сложно, согласитесь? Зато это избавляет от огромного числа операций. Платите вы за это лишним расходом памяти.

Последовательное вычисление

Теперь вернёмся к тому, с чего начали — рекурсия работает медленно. Не слишком медленно, чтобы это приносило действительные неприятности в настоящей жизни, но на соревнованиях по спортивному программированию каждая миллисекунда на счету.

Метод последовательного вычисления подходит, только если функция ссылается исключительно на элементы перед ней — это его основной, но не единственный минус. Наша задача этому условию удовлетворяет.

4–5 декабря, Онлайн, Беcплатно

Суть метода в следующем: мы создаём массив на N элементов и последовательно заполняем его значениями. Вы, наверное, уже догадались, что таким образом мы можем вычислять в том числе те значения, которые для ответа не нужны. В значительной части задач на динамику этот факт можно опустить, так как для ответа часто бывают нужны как раз все значения. Например, при поиске наименьшего пути мы не можем не вычислять путь до какой-то точки, нам нужно пересмотреть все варианты. Но в нашей задаче нам нужно вычислять приблизительно log₂(N) значений (на практике больше), для 922337203685477580-го элемента (MaxLong/10) нам потребуется 172 вычисления.

Ещё одним минусом такого подхода является сравнительно большой расход памяти.

Создание стека индексов

Сейчас нам предстоит, по сути, написать свою собственную рекурсию. Идея состоит в следующем — сначала мы проходим «вниз» от N до начальных состояний, запоминая аргументы, функцию от которых нам нужно будет вычислять. Затем возвращаемся «вверх», последовательно вычисляя значения от этих аргументов, в том порядке, который мы записали.

Зависимости вычисляются следующим образом:

Полученный размер стека – то, сколько вычислений нам потребуется сделать. Именно так я получил упомянутое выше число 172.

Теперь мы поочередно извлекаем индексы и вычисляем для них значения по формулам – гарантируется, что все необходимые значения уже будут вычислены. Хранить будем как раньше – в хэш-таблице.

Все необходимые значения вычислены, осталось только написать

Конечно, такое решение гораздо более трудоёмкое, однако это того стоит.

Хорошо, математика — это красиво. А что с задачами, в которых не всё дано?

Для большей ясности разберём следующую задачу на одномерную динамику:

На вершине лесенки, содержащей N ступенек, находится мячик, который начинает прыгать по ним вниз, к основанию. Мячик может прыгнуть на следующую ступеньку, на ступеньку через одну или через 2. (То есть, если мячик лежит на 8-ой ступеньке, то он может переместиться на 5-ую, 6-ую или 7-ую.) Определить число всевозможных «маршрутов» мячика с вершины на землю.

Идея решения

На первую ступеньку можно попасть только одним образом — сделав прыжок с длиной равной единице. На вторую ступеньку можно попасть сделав прыжок длиной 2, или с первой ступеньки — всего 2 варианта. На третью ступеньку можно попасть сделав прыжок длиной три, с первой или со втрой ступенек. Т.е. всего 4 варианта (0->3; 0->1->3; 0->2->3; 0->1->2->3). Теперь рассмотрим четвёртую ступеньку. На неё можно попасть с первой ступеньки — по одному маршруту на каждый маршрут до неё, со второй или с третьей — аналогично. Иными словами, количество путей до 4-й ступеньки есть сумма маршрутов до 1-й, 2-й и 3-й ступенек. Математически выражаясь, F(N) = F(N-1)+F(N-2)+F(N-3). Первые три ступеньки будем считать начальными состояниями.

Реализация через рекурсию

Здесь ничего хитрого нет.

Реализация через массив значений

Исходя из того, что, по большому счёту, простое решение на массиве из N элементов очевидно, я продемонстрирую тут решение на массиве всего из трёх.

Так как каждое следующее значение зависит только от трёх предыдущих, ни одно значение под индексом меньше i-3 нам бы не пригодилось. В приведённом выше коде мы записываем новое значение на место самого старого, не нужного больше. Цикличность остатка от деления на 3 помогает нам избежать кучи условных операторов. Просто, компактно, элегантно.

Там вверху ещё было написано про какую-то двумерную динамику.

С двумерной динамикой не связано никаких особенностей, однако я, на всякий случай, рассмотрю здесь одну задачу и на неё.

В прямоугольной таблице NxM в начале игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). Посчитайте, сколько есть способов у игрока попасть в правую нижнюю клетку.

Идея решения

Логика решения полностью идентична таковой в задаче про мячик и лестницу — только теперь в клетку (x,y) можно попасть из клеток (x-1,y) или (x, y-1). Итого F(x,y) = F(x-1, y)+F(x,y-1). Дополнительно можно понять, что все клетки вида (1,y) и (x,1) имеют только один маршрут — по прямой вниз или по прямой вправо.

Реализация через рекурсию

Ради всего святого, не нужно делать двумерную динамику через рекурсию. Уже было упомянуто, что рекурсия менее выгодна, чем цикл по быстродействию, так двумерная рекурсия ещё и читается ужасно. Это только на таком простом примере она смотрится легко и безобидно.

Реализация через массив значений

Классическое решение динамикой, ничего необычного — проверяем, является ли клетка краем, и задаём её значение на основе соседних клеток.

Отлично, я всё понял. На чём мне проверить свои навыки?

В заключение приведу ряд типичных задач на одномерную и двумерную динамику, разборы прилагаются.

Взрывоопасность

При переработке радиоактивных материалов образуются отходы двух видов — особо опасные (тип A) и неопасные (тип B). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A. Стопка считается безопасной, если она не является взрывоопасной. Для заданного количества контейнеров N определить количество возможных типов безопасных стопок.

Решение

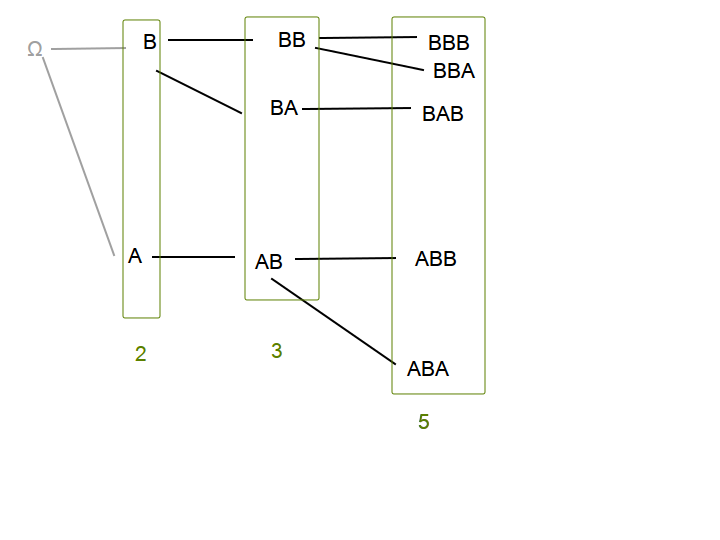
Ответом является (N+1)-е число Фибоначчи. Догадаться можно было, просто вычислив 2-3 первых значения. Строго доказать можно было, построив дерево возможных построений.

Каждый основной элемент делится на два — основной (заканчивается на B) и побочный (заканчивается на A). Побочные элементы превращаются в основные за одну итерацию (к последовательности, заканчивающейся на A, можно дописать только B). Это характерно для чисел Фибоначчи.

Реализация

Подъём по лестнице

Мальчик подошел к платной лестнице. Чтобы наступить на любую ступеньку, нужно заплатить указанную на ней сумму. Мальчик умеет перешагивать на следующую ступеньку, либо перепрыгивать через ступеньку. Требуется узнать, какая наименьшая сумма понадобится мальчику, чтобы добраться до верхней ступеньки.

Решение

Очевидно, что сумма, которую мальчик отдаст на N-ой ступеньке, есть сумма, которую он отдал до этого плюс стоимость самой ступеньки. «Сумма, которую он отдал до этого» зависит от того, с какой ступеньки мальчик шагает на N-ую — с (N-1)-й или с (N-2)-й. Выбирать нужно наименьшую.

Реализация

Калькулятор

Имеется калькулятор, который выполняет три операции:

Определите, какое наименьшее число операций необходимо для того, чтобы получить из числа 1 заданное число N. Выведите это число, и, на следующей строке, набор исполненных операций вида «111231».

Решение

Наивное решение состоит в том, чтобы делить число на 3, пока это возможно, иначе на 2, если это возможно, иначе вычитать единицу, и так до тех пор, пока оно не обратится в единицу. Это неверное решение, т.к. оно исключает, например, возможность убавить число на единицу, а затем разделить на три, из-за чего на больших числах (например, 32718) возникают ошибки.

Правильное решение заключается в нахождении для каждого числа от 2 до N минимального количества действий на основе предыдущих элементов, иначе говоря: F(N) = min(F(N-1), F(N/2), F(N/3)) + 1. Следует помнить, что все индексы должны быть целыми.

Для воссоздания списка действий необходимо идти в обратном направлении и искать такой индекс i, что F(i)=F(N), где N — номер рассматриваемого элемента. Если i=N-1, записываем в начало строки 1, если i=N/2 — двойку, иначе — тройку.

Реализация

Самый дешёвый путь

В каждой клетке прямоугольной таблицы N*M записано некоторое число. Изначально игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). При проходе через клетку с игрока берут столько килограммов еды, какое число записано в этой клетке (еду берут также за первую и последнюю клетки его пути).

Требуется найти минимальный вес еды в килограммах, отдав которую игрок может попасть в правый нижний угол.

Решение

В любую клетку таблицы мы можем попасть либо из клетки, находящейся непосредственно над ней, либо из клетки, находящейся непосредственно слева. Таким образом, F(x,y) = min(F(x-1,y), F(x,y-1)). Чтобы не обрабатывать граничные случаи, можно добавить первую строку и столбец, заполненные некоторой константой — каким-то числом, заведомо большим содержимого любой из клеток.

Источник