что такое дифракция френеля

Дифракция Френеля

Дифра́кция Френе́ля — дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.

Дифракционная картина для дифракции Френеля зависит от расстояния между экранами и от расположения источников света. Её можно рассчитать, считая, что каждая точка на границе апертуры излучает сферическую волну по принципу Гюйгенса. В точке наблюдения (занимаемое вторым экраном) волны или усиливают друг друга, или гасятся в зависимости от разности хода.

Содержание

Интеграл Френеля

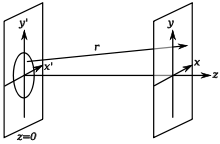
В скалярной теории дифракции распределение электрического поля дифрагирующего света в точке (x,y,z) задаётся выражением Релея-Зоммерфельда:

где , — мнимая единица, и — косинус угла между направлениями z и r. В аналитическом виде этот интеграл представим, только для простейших геометрий отверстий, поэтому он вычисляется обычно численными методами.

Аппроксимация Френеля

Главная трудность при вычислении интеграла представляет собой выражение для r. Во-первых, упростим вычисления, сделав замену переменных:

Подставляя это выражение вместо r, найдём:

и выразим r в виде

Выражая k в терминах длины волны,

получим следующее соотношение:

Умножая обе стороны на , получим

Это выражение называется приближением Френеля, а неравенство полученное ранее есть условие применимости этого приближения.

Дифракция Френеля

Условие применимости достаточно слабо, и позволяет все характерные размеры взять как сравнимые величины, если апертура много меньше, чем длина пути. К тому же так как нас интересует только малая область недалеко от источника величины x и y много меньше чем z, предположим , что означает и r в знаменателе можно аппроксимировать выражением .

В противоположность дифракции Фраунгофера, дифракция Френеля должна учитывать кривизну волнового фронта, для того чтобы правильно учесть относительные фазы интерферирующих волн.

Электрическое поле для дифракции Френеля в точке (x,y,z) дано в виде:

Примечания

Литература

Внешние ссылки

См. также

Полезное

Смотреть что такое «Дифракция Френеля» в других словарях:

дифракция Френеля — Дифракция света, наблюдаемая на таких расстояниях, при которых угловые размеры оптической неоднородности много больше отношения длины световой волны к линейным размерам этой неоднородности. [Сборник рекомендуемых терминов. Выпуск 79. Физическая… … Справочник технического переводчика

дифракция Френеля — Frenelio difrakcija statusas T sritis fizika atitikmenys: angl. Fresnel diffraction vok. Fresnelsche Beugung, f rus. дифракция Френеля, f pranc. diffraction de Fresnel, f … Fizikos terminų žodynas

Дифракция — первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных макси … Википедия

Дифракция волн — (лат. diffractus буквально разломанный, переломанный) явление, которое можно рассматривать как отклонение от законов геометрической оптики при распространении волн. Первоначально понятие дифракции относилось только к огибанию волнами… … Википедия

Дифракция света — явления, наблюдающиеся при распространении света мимо резких краёв непрозрачных или прозрачных тел, сквозь узкие отверстия. При этом происходит нарушение прямолинейности распространения света, т. е. отклонение от законов геометрической… … Большая советская энциклопедия

Дифракция Фраунгофера — Пример оптической установки, в которой наблюдаются дифракция Френеля (в ближней зоне) и дифракция Фраунгофера (в … Википедия

ДИФРАКЦИЯ СВЕТА — в узком (наиболее употребительном) смысле явление огибания лучами света контура непрозрачных тел и, следовательно, проникновение света в область геом. тени; в широком смысле проявление волновых св в света в условиях, близких к условиям… … Физическая энциклопедия

ДИФРАКЦИЯ ВОЛН — (от лат. diffractus разломанный, преломлённый), в первоначальном узком смысле огибание волнами препятствий, в современном более широком любое отклонение при распространении волн от законов геометрической оптики. При таком общем толковании Д. в.… … Физическая энциклопедия

Источник

Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля

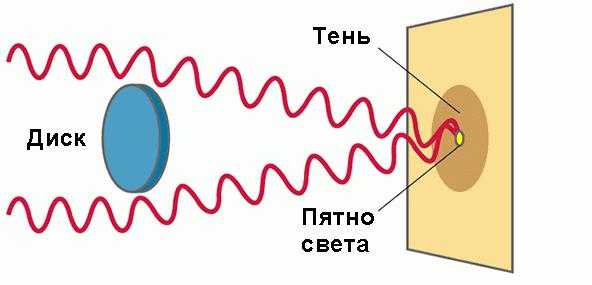
Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.

Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.

Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.

Принцип Гюйгенса-Френеля

Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.

Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.

Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.

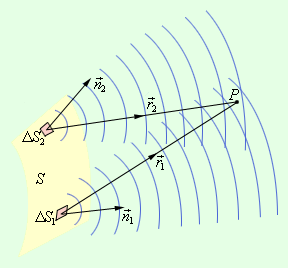
Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сферам.

Для примера ниже приведена дифракционная задача прохождения плоской монохроматической волны, которая исходит от удаленного источника через отверстие с радиусом R непрозрачного экрана.

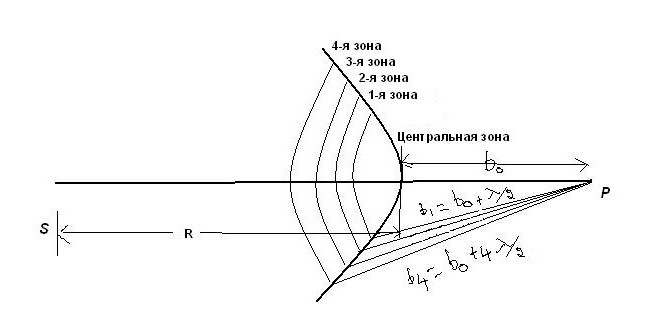
Чтобы расчеты были облегченными, волновая поверхность падающей волны разбивается на кольцевые зоны, называемыми зонами Френеля, исходя из правила: расстояния от границ соседних зон к точке Р имеют отличие на половину волны.

Зоны Френеля. Интерференционный максимум

Отличие от двух соседних точек расстоянием λ 2 говорит о том, что колебания, возбуждаемые этими зонами в состоянии противофазы. Соседние волны начинают гасить друг друга, а это приводит к тому, что суммарная амплитуда в точке запишется как:

Выражения в скобках равняются нулю, значит, амплитуда, вызванная волновым фронтом, равняется половине действий первой зоны.

Полученные пластинки обладают свойством фокусировки света, поэтому их называют зонными пластинками.

Круглый диск дает понять, что при дифракции зоны Френеля от 1 до m будут в закрытом состоянии. Отсюда получаем, что формула амплитуды колебаний примет вид:

Так как оптический диапазон имеет короткую волну, тогда соответственно зона Френеля также мала. Отчетливее проявление дифракционных явлений заметно при небольшом количестве зон на препятствии.

Получим формулы вида:

Когда количество зон Френеля из препятствия увеличивается, тогда дифракционные явления становятся незаметными:

Определение границы применимости геометрической оптики возможно при помощи заданного неравенства. При выполнении данного условия узкий пучок света может быть сформирован.

Отсюда следует вывод, что волновая оптика – это предельный случай геометрической.

При расчете видно, что радиусы ρ m зон Френеля на волне сферического фронта запишется, как

Выводы по теории Френеля справедливы.

Дифракция и интерференция света применима к любым волнам, так как имеется общность закономерностей. Начало XIX века – это было время, когда ученые только начинали изучать волны, а физическая природа света еще не была раскрыта.

Источник

Что такое дифракция френеля

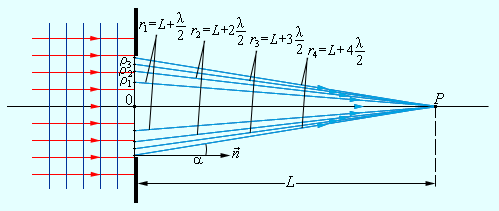
Определить понятие зоны Френеля можно для дифракции на отверстии любой формы и даже вообще без отверстия, но практически полезно рассмотрение зон Френеля только при дифракции на круглом отверстии, причем в случае, когда источник света и точка наблюдения находятся на прямой, перпендикулярной к плоскости экрана с отверстием и проходящей через центр отверстия.

Если оба расстояния и гораздо больше диаметра отверстия, а обычно рассматривают именно такой случай, то из геометрических соображений (рис. 36) можно получить

Картина построения на комплексной плоскости совершенно аналогична картине для дифракции Фраунгофера на одной щели.

Рассмотрим теперь, как изменяется картина сложения комплексных амплитуд при изменении радиуса отверстия и сохранении остальных параметров задачи.

Если отверстие открывает две зоны Френеля, то картина сложения амплитуд будет иметь вид окружности. В этом случае суммарная амплитуда света в точке равна нулю (нулевая длина хорды).

Если открыто три зоны Френеля, то картина представляет собой полторы окружности, и так далее.

Для четного числа зон Френеля амплитуда в точке наблюдения равна нулю. Для нечетного числа амплитуда одинаковая, максимальная и равна длине диаметра окружности на комплексной плоскости сложения амплитуд.

Иногда в условии задачи говорится, что открыто какое-либо дробное число зон Френеля. При этом под половиной зоны Френеля понимают четверть окружности картины сложения амплитуд, что соответствует половине площади, а не радиуса, первой зоны Френеля. Аналогично для любого другого дробного числа зон Френеля. Для половины зоны Френеля, как видно из рис. 38, амплитуда поля в корень из двух раз меньше, чем для одной зоны Френеля.

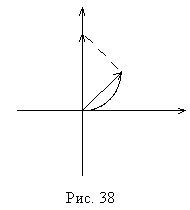
Иногда в задачах говорится, что какое-то (дробное) число зон закрыто, затем сколько-то зон открыто и остальные закрыты. Тогда суммарную амплитуду поля можно найти, как векторную разность амплитуд двух задач.

Если открыты все зоны Френеля (нет препятствия на пути световой волны), то картина сложения амплитуд будет выглядеть как спираль, что очень грубо изображено на рис. 39. Спираль получается, потому что при большом числе открытых зон следует учитывать зависимость амплитуды света излученного вторичным источником от расстояния до точки наблюдения и от направления излучения вторичного источника. В результате, свет от зон с большим номером будет иметь малую амплитуду.

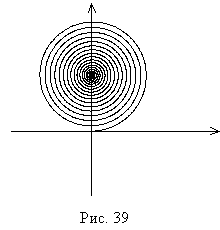
Центр спирали находится в середине окружности из первых двух зон, поэтому амплитуда поля при всех открытых зонах вдвое меньше, чем амплитуда поля при открытой одной первой зоне, а интенсивности различаются в четыре раза. Интенсивность света при открытой первой зоне Френеля в четыре раза больше интенсивности света перед экраном с отверстием.

Дифракция Фраунгофера.

Дифракция Френеля.

Сравнение линзы и зонной пластинки.

Если закрыть все четные, или все нечетные, зоны Френеля, то в точке наблюдения будет свет с большой амплитудой. Действительно, каждая зона дает пол окружности на плоскости сложения комплексных амплитуд. Если оставить открытыми только нечетные зоны, то от общей спирали сложения амплитуд (рис. 39) останутся только половинки окружностей (рис. 40), дающие вклад «снизу вверх» в суммарную амплитуду поля.

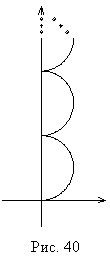
Препятствие на пути световой волны, в котором открыты только четные или только нечетные зоны Френеля, называется зонной пластинкой. Интенсивность света в точке наблюдения за зонной пластинкой многократно превышает интенсивность света, падающего на зонную пластинку. Причина этого в том, что свет от каждой открытой зоны Френеля приходит в точку наблюдения в одной и той же фазе. Ситуация похожа на фокусировку света линзой.

Линза в отличии от зонной пластинки никакие зоны Френеля не закрывает, она сдвигает по фазе на свет от тех зон, которые закрывает зонная пластинка. За счет этого амплитуда света удваивается. Кроме того линза устраняет взаимные фазовые сдвиги световых волн, проходящих внутри одной зоны Френеля. Она разворачивает пол окружности на комплексной плоскости для каждой зоны Френеля в отрезок прямой линии. За счет этого амплитуда возрастает еще в раз. В результате всю спираль сложения комплексных амплитуд на комплексной плоскости линза разворачивает в прямую линию.

Как линза выравнивает фазы дифрагированных волн? Линза выравнивает оптическую длину пути различных лучей, от источника до изображения. Это, в свою очередь, возможно потому, что оптическая длина пути в стекле в раз больше геометрической длины.

Получение изображения точечного источника с помощью линзы можно рассматривать или по правилам геометрической оптики, или как результат дифракции и интерференции волн, проходящих через различные участки линзы. В последнем случае большая интенсивность света в точке изображения получается, как результат интерференции волн, прошедших через разные участки линзы и пришедших в точку изображения в одинаковой фазе. В другие точки за линзой свет приходит через различные участки линзы в различных фазах, поэтому интенсивность света в других точках намного меньше, чем в точке изображения.

Дифракционный предел разрешения.

Более строгая теория для некогерентного освещения объекта дает выражение

Величину называют числовой апертурой.

Явление дифракции также ограничивает спектральное разрешение спектрометра. Вспомните нормальную ширину щели.

VII. ЗАКЛЮЧЕНИЕ.

В заключении сделаем несколько замечаний о полезности применения соображений размерности.

Многие соотношения в оптике, как и вообще в физике, могут быть получены путем построения простейшей зависимости требуемых величин с учетом необходимой размерности результата.

Подробнее смотрите литературу [2, 3].

VIII. ЛИТЕРАТУРА.

2. Бутиков Е.И. Оптика: Учеб. пособие для вузов/ Под ред. Н.И. Калитеевского.- М.: Высш. шк., 1986. 512с.

3. Борн М., Вольф Э. Основы оптики. М.: Наука, 1973. 720с.

Источник

СОДЕРЖАНИЕ

Ранние методы лечения этого явления

Некоторые из самых ранних работ по так называемой дифракции Френеля были выполнены Франческо Марией Гримальди в Италии в 17 веке. В своей монографии под названием «Свет» Ричард К. Маклаурин объясняет дифракцию Френеля, задавая вопрос о том, что происходит при распространении света и как на этот процесс влияет, когда барьер с прорезью или отверстием в нем вставляется в луч, создаваемый удаленным источником света. свет. Он использует принцип Гюйгенса, чтобы исследовать, говоря классическим языком, то, что происходит. Фронт волны, который проходит от щели к экрану обнаружения на некотором расстоянии, очень близко приближается к фронту волны, исходящей из области щели, без учета каких-либо мельчайших взаимодействий с реальным физическим краем.

В результате, если зазор очень узкий, могут возникать только дифракционные картины с яркими центрами. Если зазор постепенно увеличивать, то дифракционные картины с темными центрами будут чередоваться с дифракционными картинами с яркими центрами. По мере увеличения зазора различия между темными и светлыми полосами уменьшаются до тех пор, пока дифракционный эффект больше не будет обнаруживаться.

Дифракционный интеграл Френеля

Картина дифракции электрического поля в точке (x, y, z) определяется выражением:

Аналитическое решение этого интеграла невозможно для всех, кроме простейших дифракционных геометрий. Поэтому обычно его рассчитывают численно.

Приближение Френеля

Затем по биномиальному разложению

выражая k через длину волны,

получаем следующие отношения:

ρ 4 λ 4 ≪ 8 z 3 λ 3 <\ displaystyle <\ frac <\ rho ^ <4>> <\ lambda ^ <4>>> \ ll 8 <\ frac > <\ lambda ^ <3>>>>

Для приложений, использующих оптические длины волн, длина волны λ обычно на много порядков меньше соответствующих физических размеров. В частности:

Таким образом, с практической точки зрения требуемое неравенство всегда будет выполняться до тех пор, пока

Затем мы можем аппроксимировать выражение только двумя первыми членами:

Дифракция Френеля

Для дифракции Френеля электрическое поле в точке (x, y, z) тогда определяется как:

Альтернативные формы

Свертка

Интеграл можно выразить другими способами, чтобы вычислить его, используя некоторые математические свойства. Если мы определим следующую функцию:

тогда интеграл можно выразить в виде свертки :

другими словами, мы представляем распространение с помощью моделирования с линейным фильтром. Вот почему мы можем назвать функцию h (x, y, z) импульсной характеристикой распространения в свободном пространстве.

преобразование Фурье

и развернуть каждую составляющую поперечного смещения:

тогда мы можем выразить интеграл через двумерное преобразование Фурье. Воспользуемся следующим определением:

Линейное каноническое преобразование

Смотрите также

Заметки

Источник

Дифракция Френеля на круглом отверстии и диске

Дифракция света проявляется в огибании световыми волнами небольших препятствий, при этом наблюдаются отклонения от законов геометрической оптики. Это также относится и к световым волнам, проходящим через отверстие, например, в объективе фотокамеры или через зрачок глаза. Есть дифракция Френеля и Фраунгофера. Различия состоят в величине расстояния между источником света, препятствием и экраном, на котором наблюдается картина этого явления.

Место дифракции в общем ряду оптических явлений

Прохождение световых (и вообще электромагнитных) волн через различные неоднородные среды сопровождается явлениями их отражения, дифракции и преломления. Когда волна достигает границы двух сред, она разделяется на отраженную, остающуюся в исходной среде, но с изменением направления распространения, и преломленную, которая проходит через границу сред, но также с изменением направления. Дифракция Френеля — это процесс изменения в направлении световой волны при встрече на своем пути не границы двух сред, а некоторого непрозрачного препятствия с отверстием (или без него, но небольших размеров) в той же среде. Степень дифракции увеличивается с ростом длины световой волны.

Открытие явления

Знаменитым сделала Гримальди его работа под названием «Физическая наука о свете, цветах и радуге», которая была опубликована в Болонье в 1665 году. Большая ее часть состоит из утомительного обсуждения природы света с теологических позиций и сегодня не представляет интереса. Однако, кроме этого, в книге содержатся учетные записи многочисленных экспериментов, связанных с дифракцией лучей света.

Исходя из повседневного опыта, люди еще в древности сделали вывод, что лучи света распространяются по прямым линиям. Ведь предмет, находящийся между, например, пламенем свечи и стеной, отбрасывает тень с резкой границей, как если бы прямые лучи света обрывались на непрозрачной преграде.

Однако результаты опытов Гримальди противоречили этим устоявшимся за тысячелетия представлениям. Оказывается, если освещать разные предметы через преграду с маленьким отверстием, то тени от них будут вовсе не такими, как при отсутствии преграды. Получалось, что свет способен менять направление распространения и огибать небольшие препятствия.

Как была обнаружена дифракция Френеля на круглом отверстии

Гримальди, пропустив свет солнца в темную комнату через небольшое отверстие (апертуру), заметил, что ширина тени тонких объектов вроде иглы и волоса на экране оказывается значительно большей (как видно на фото ниже), чем это было бы, если бы лучи света проходили по прямым линиям.

Он отметил также, что круг света, формируемый на экране лучами, проходящими через очень небольшое отверстие в пластине свинца, был явно больше, чем это было бы, если бы эти лучи падали на экран прямолинейно. Гримальди пришел к выводу, что они изменяют свое направление при прохождении вблизи краев отверстия.

В его опытах, проводившихся внутри одной комнаты, свет в которую попадал через отверстия в ставнях, расстояние между препятствием для световых волн (пластина с круглым отверстием) и экраном было малым. Этим условиям соответствует и такое явление, как дифракция Френеля. Анализируя ее, нельзя пренебрегать кривизной фронта как исходной падающей на препятствие волны, так и вторичных волн. Именно они дают на экране дифракционное изображение препятствия с отверстием, как показано на фото ниже.

Что происходит, если свет падает на небольшое непрозрачное препятствие

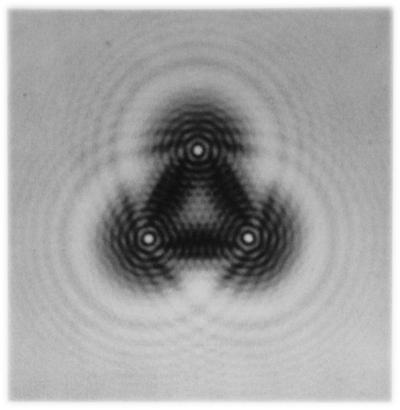
Гримальди обнаружил также, что тень небольшого тела (неправильной формы) была окружена тремя цветными полосами или лентами, которые становились более узкими по мере удаления от центра тени. Если исходный поток света был более сильным, он воспроизводил аналогичные цветные полосы и в зоне самой тени: там оказывались две или более таких полос, причем их число увеличивалось пропорционально расстоянию между тенью и освещаемым телом.

И в этом случае Гримальди удалось наблюдать явление, которое позже было названо «дифракция Френеля», в результате которого на экране получалась дифракционная картина препятствия. Аналитически рассчитать ее очень трудно. Впрочем, имеются методы, которые позволяют в некоторых частных случаях существенно упростить этот расчет.

И еще одно замечание об опытах Гримальди. Если бы он использовал в них в качестве экрана круглый диск (например, блюдце), то, возможно, ему удалось бы на полтора столетия раньше, чем это случилось в действительности, наблюдать такое явление, как дифракция Френеля на круглом диске. Но история вообще и история науки в частности не знают сослагательного наклонения. Поэтому данный опыт был выполнен только в начале 19 в. (см. ниже).

Первое наблюдение интерференции

Пропустив солнечные лучи в комнату через несколько маленьких круглых отверстий, Гримальди получил следы перекрывающихся друг другом конусов света на экране. Как и следовало ожидать, в тех областях, на которые падали лучи от двух отверстий, экран был освещен сильнее, чем это было бы от одного конуса света; но исследователь был удивлен, обнаружив, что те части суммарной тени, в которых конусы света наложены друг на друга, оказались темнее, чем соответствующие части, в которых не было никакого наложения (рисунок ниже).

От Гримальди до Гюйгенса и Ньютона

Первую попытку объяснить причину отклонения света от прямолинейного распространения предпринял знаменитый английский ученый Р. Гук. Он предположил, что свет – это волновые колебания мирового эфира, под которым тогда понималась всепроникающая субстанция, заполняющая все пространство. В идее Гука уже была заложена основа для будущего правильного объяснения того, что такое дифракция Френеля и все оптические явления. Однако он не смог создать соответствующую количественную теорию.

Следующий шаг был сделан Христианом Гюйгесом, который сформулировал свой знаменитый принцип в 1690 г. Согласно ему, видимый свет есть совокупность распространяющихся от источника во все стороны сферических волн в эфире. При этом источником этих волн могут быть не только частицы эфира, возбужденные непосредственно источником света (например, пламенем свечи), но и любые другие его частицы в точках пространства, которые проходит свет при распространении. Результирующая видимая волна находится в любой момент времени как огибающая все вторичные волны. Последние же вполне могут распространяться и за границы препятствий на пути света, что хорошо накладывается на наблюдаемые при дифракции картины их теней. Поэтому, согласно этой теории, никакого огибания светом препятствий попросту нет – от новых (вторичных) источников он распространяется за препятствия.

Однако, согласно принципу Гюйгенса, вообще невозможны узкие световые лучи – их края сразу же должны расползаться во все стороны. Тем не менее, их можно видеть невооруженным глазом, как это было в опытах Гримальди. Возникало противоречие между теорией и практикой.

Возвращение световых волн

В 1880 г. английский физик Т. Юнг предложил вернуться к волновой теории света, дополненной понятием об интерференции световых волн. Оно означает, что при наложении друг на друга когерентных (с одинаковыми частотами) волн возможно устойчивое во времени усиление интенсивности света в одних точках поля и ослабление в других в зависимости от соотношения фаз складываемых световых волн.

Понятием интерференции воспользовался французский физик О. Френель, чтобы дополнить им принцип Гюйгенса. Согласно его варианту, все вторичные сферические волны являются когерентными и интерферируют при наложении. Какой же физический механизм имеет дифракция Гюйгенса-Френеля?

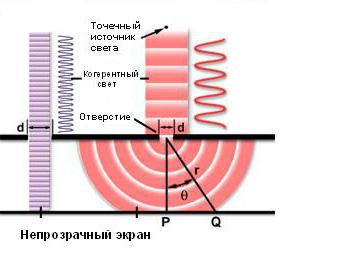
Пропускаем свет через круглое отверстие

Когда световая волна распространяется через отверстие, соотношение между его диаметром и длиной волны падающего луча определяет поведение света. Как показано на левой части рисунка ниже, когда длина волны значительно меньше, чем диаметр отверстия, она просто проходит вперед по прямой линии, как будто препятствия вообще нет.

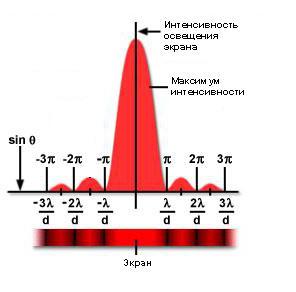
На правой стороне рисунка, однако, показана другая ситуация. В этом случае длина волны света, прошедшего от точечного источника, превышает диаметр проема, и возникает дифракция Френеля на отверстии. При анализе этого явления отверстие считают отсутствующим, а вместо него помещают совокупность фиктивных вторичных источников света, которые возбуждают те самые вторичные сферические волны, о которых уже упоминалось выше. Они распространяются в направлении экрана и достигают разных его точек с разными фазами, интерферируя друг с другом, т. е. усиливаясь или ослабляясь в каждой такой точке. Поскольку вся система обладает осевой симметрией, то падающий цилиндрический пучок света превращается в конический, а на экране наблюдается также осесимметричная дифракционная картина из чередующихся ярких и темных колец, называемых также максимумами и минимумами освещенности соответственно. В точке P, находящейся на оси отверстия, будет яркое пятно – основной максимум, а первый из вторичных максимумов освещенности возникнет в точке Q. Интенсивность вторичных максимумов уменьшается по мере увеличения их расстояния от центра дифракционной картины. Соотношение между размером отверстия и степенью дифракции определяется следующим уравнением:

Рисунок ниже показывает, как изменяется интенсивность освещенности экрана в зависимости от углового расстояния от центра. Обратите внимание, что минимумы, находящиеся между вторичными максимумами, расположены в точках, кратных величине ∏.

Аналитический расчет картины такого явления, как дифракция Френеля на отверстии и диске, существенно упрощается вследствие осевой симметрии, о чем будет дополнительно сказано ниже.

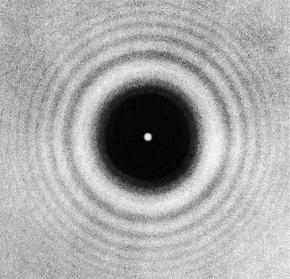
Круглый диск на пути пучка света

Если следовать теории Френеля, то при помещении на пути пучка света круглого непрозрачного диска все точки на его краях становятся источниками когерентных вторичных сферических волн. Расстояния между этими точками и точкой пересечения оси диска с перпендикулярным ей непрозрачным экраном одинаковы. Поэтому волны от всех точек на краю диска должны пересечься в одно время и в одной фазе, т. е. они должны сложиться и значительно усилить друг друга. Получается, что в центре круглой тени от диска должно наблюдаться яркое освещенное пятно, как на рисунке ниже.

Так проявляет себя дифракция Френеля на диске. Яркое же пятно в центре его тени получило наименование пятна Пуассона. Если диск небольшой, то интенсивность света в центре его дифракционного изображения практически такая же, как и при его (диска) отсутствии.

Как рассчитывать картины дифракции

В общем случае расчет интерференции вторичных волн для получения дифракционной картины является сложным. Но в осесимметричных случаях он может быть упрощен, так что становится несложной и вся картина такого явления, как дифракция. Метод зон Френеля позволяет наглядно геометрическим способом разбить фронт сферической волны на кольцевые участки.

Амплитуды и относительные фазы всех зон принимаются во внимание для расчета распределения интенсивности. Таким образом, для определения дифракционной картины применяется достаточно сложная математическая обработка. Но при анализе такого явления, как дифракция Френеля на круглом отверстии и диске, она существенно упрощается.

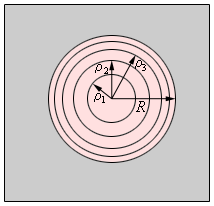
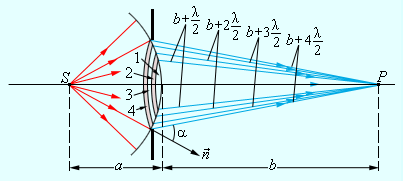
На рисунке ниже S является точечным источником света.

Первая зона находится на расстоянии b₁ = b₀ + λ/2; вторая: b₂ = b₀ + 2λ/2; третья: b₃ = b₀ + 3λ /2; i-я зона: b_i = b₀ + iλ /2.

Последовательно расположенные края двух соседних зон находятся в сходственных точках. Если в них возбуждаются вторичные сферические волны, то они приходят в точку наблюдения Р с разностью фаз в 180° и взаимно ослабляют друг друга при наложении (но не уничтожают).

Как работают кольцевые зоны Френеля на круглом отверстии

Рассмотрим снова случай, когда на круглом отверстии происходит дифракция света. Зоны Френеля, на которые может быть разбит волновой фронт, укладывающиеся в отверстии данного диаметра при определенной длине волны λ и расстоянии от фронта до экрана b₀, могут оказаться в количестве, выраженном нечетным или четным числом. Как уже было отмечено выше, вторичные волны от двух соседних зон в каждой точке экрана ослабляют, хотя и не уничтожают друг друга. Поэтому, если для центра дифракционной картины число зон Френеля, укладывающихся в отверстии, нечетно (2k+1), то амплитуда освещенности в центре картины будет складываться из суммы остатка действия первой (центральной) зоны и ничем не скомпенсированного действия (2k+1)-й зоны, которые будут усиливать друг друга. Дифракционная картина для этого случая показана на рисунке ниже.

Если же число зон Френеля, укладывающихся в отверстии, будет четным, то влияние всех зон в центре картины будет взаимно попарно скомпенсировано, и в нем появится темное пятно.

Источник