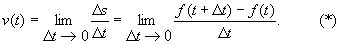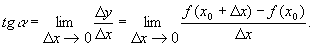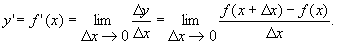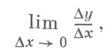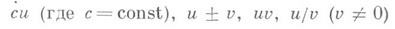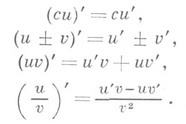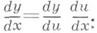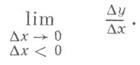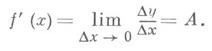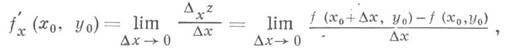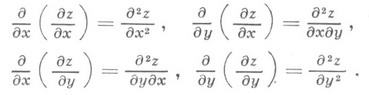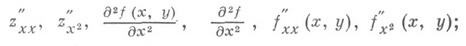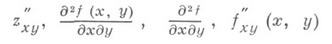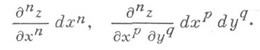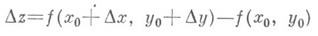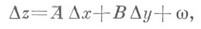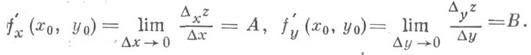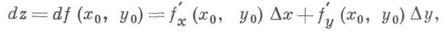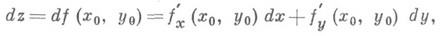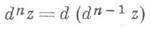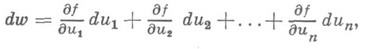что такое дифференциальное исчисление

Дифференциальное исчисление

Полезное

Смотреть что такое «Дифференциальное исчисление» в других словарях:

Дифференциальное исчисление — Дифференциальное исчисление раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Содержание 1 Дифференциальное исчисление функций одной переменной … Википедия

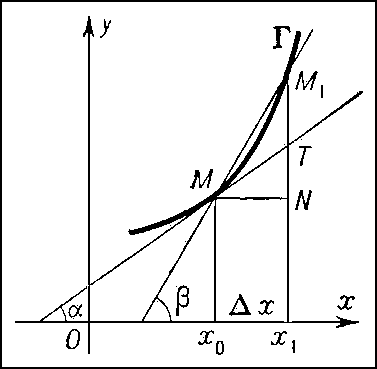
Дифференциальное исчисление — Дифференциальное исчисление. Проведение касательной к графику функции y=f(x) в точке M. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ, раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной… … Иллюстрированный энциклопедический словарь

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — математическая наука, занимающаяся изучением дифференциалов функций, т. е. выражений, показывающих, в какой зависимости переменные величины находятся друг от друга. Дифференциалом функции назыв. бесконечно малое приращение, получаемое ею,… … Словарь иностранных слов русского языка

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ, см. ИСЧИСЛЕНИЕ … Научно-технический энциклопедический словарь

дифференциальное исчисление — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN differential calculus … Справочник технического переводчика

дифференциальное исчисление — раздел математики, в котором изучаются производные, дифференциалы и их применения к исследованию свойств функций. Производной функции у = f(х) называется предел отношения приращения Δу = у1 – у0 функции к приращению Δх = x1 – х0 аргумента при Δх … Энциклопедический словарь

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — на аналитических пространствах обобщение классич. исчисления дифференциальных форм и дифференциальных операторов на случай аналитич. ространств. Об исчислении дифференциальных форм на комплексных многообразиях см. Дифференциальная форма. Пусть… … Математическая энциклопедия

Дифференциальное исчисление — Исчисление бесконечно малых, включающее так называемое Д. исчисление, а также ему обратное интегральное, принадлежит к числу наиболее плодотворных открытий человеческого ума и составило эпоху в истории точных наук. Ближайшим поводом к изобретению … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Дифференциальное исчисление

Из Википедии — свободной энциклопедии

Дифференциальное исчисление — раздел математического анализа, в котором изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Формирование дифференциального исчисления связано с именами Исаака Ньютона и Готфрида Лейбница. Именно они чётко сформировали основные положения и указали на взаимообратный характер дифференцирования и интегрирования. Создание дифференциального исчисления (вместе с интегральным) открыло новую эпоху в развитии математики. С этим связаны такие дисциплины как теория рядов, теория дифференциальных уравнений и многие другие. Методы математического анализа нашли применение во всех разделах математики. Очень распространилась область применения математики в естественных науках и технике.

Дифференциальное исчисление базируется на таких важнейших понятиях математики, определение и исследование которых и составляют предмет введения в математического анализа: действительные числа (числовая прямая), функция, граница, непрерывность. Все эти понятия получили современную трактовку в ходе развития и обоснования дифференциального и интегрального исчислений.

Основная идея дифференциального исчисления состоит в изучении функции в малом. Точнее дифференциальное исчисление дает аппарат для исследования функций, поведение которых в достаточно малой окрестности каждой точки близка к поведению линейной функции или многочлена. Таким аппаратом служат центральные понятия дифференциального исчисления: производная и дифференциал.

Источник

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

— раздел математики, в к-ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу математич. анализа, имеющего чрезвычайное значение для естествознания и техники. Основной предпосылкой для создания Д. и. явилось введение в математику переменных величин (Р. Декарт, R. Descartes). В общих чертах построение дифференциального и интегрального исчислений было завершено в трудах И. Ньютона (I. Newton) и Г. Лейбница (G. Leibniz) к концу 17 в., однако вопросы обоснования с помощью понятия пре-

Производная. Пусть функция y=f(x). определена в нек-рой окрестности точки х ₀, есть приращение аргумента, Dy=f(x₀+Dx)-f(x₀).— соответствующее приращение функции.Если существует (конечный или бесконечный) предел

то он наз. производной функции f(x). в точке х ₀ и обозначается у’, у’ _х, Итак, по определению,

в случае касательная образует с Ох прямой угол (см. рис. 2). Таким образом, производная непрерывной функции f(x)в точке х ₀ совпадает с угловым коэффициентом tga касательной к кривой, заданной уравнением у=f(x), в ее точке с абсциссой х ₀.

Механичес кое истолков а ние производной. Пусть точка Мдвижется прямолинейно по закону s=f(t). За время Dt точка Мсместится на Ds=f(t+Dt)-f(t). Отношение Ds/Dt представляет собой среднюю скорость u _ср точки за время Dt. При неравномерном движении u_cp не постоянна. Мгновенной скоростью в момент tназ. предел средней скорости при т. е. u=f’(t). (в предположении, что эта производная существует).

Таким образом, понятие производной доставляет общее решение задачи о построении касательной к плоской кривой и задачи о вычислении скорости прямолинейного движения. Эти две задачи явились основными предпосылками в формировании понятия производной.

Функция, имеющая в точке х ₀ конечную производную, непрерывна в этой точке. В случае бесконечной производной этого может не быть. Непрерывная функция может не иметь ни конечной, ни бесконечной производной. Существуют непрерывные функции, не имеющие производной ни в одной точке области определения. Для производных основных элементарных функций справедливы следующие формулы (в любой точке области определения; исключения оговариваются):

Имеют место также следующие правила дифференцирования;

1) Если функции и(х)и u(х)дифференцируемы в точке х ₀, то функции

также дифференцируемы в этой точке, причем

2) Теорема о производной сложной функции: если функция y=f(u)дифференцируема в точке и ₀, а функция j(х)дифференцируема в точке х ₀, причем u₀=j(x_o), то сложная функция y-f(j(x))дифференцируема в точке х ₀ и y’_x=f(u₀)j'(x₀) или, в другой записи,

3) Теорема о производной обратнойфункции: если y=f(x)и x=g(y)- две взаимно обратные возрастающие (или убывающие) функции, заданные на нек-рых интервалах, и существует конечная производная то в точке y₀=f(z₀ )существует конечная производная или, в другой записи, Эта теорема допускает обобщение: если, при выполнении прочих условий, f’ (x₀) =0(f’ ( х _о)= ), то g’( у _о)= (соответственно g’( у ₀)=0).

Односторонние производные. Если в точке х ₀ существует предел

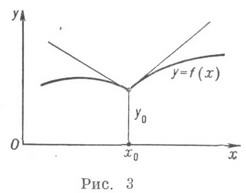
Функция f(x)имеет производную в точке х ₀ в том и только в том случае, если в этой точке существуют равные между собой правая и левая производные. Для непрерывной функции существование в точке правой (соответственно левой) производной равносильно существованию в соответствующей точке ее графика правой (соответственно левой) односторонней полукасательной с угловым коэффициентом, равным значению этой односторонней производной. Точки, в к-рых полукасательные не образуют одну прямую, называются угловыми точками (см. рис. 3).

Функция y=f(x)имеет в точке хдифференциал в том и только в том случае, если она имеет в этой точке конечную производную

Функция, для к-рой существует дифференциал, наз. дифференцируемой в рассматриваемой точке. Таким образом, дифференцируем ость функции означает одновременно и существование дифференциала, и существование конечной производной. При этом dy = df(x)=f’(x)Ax. Для независимого переменного хполагают dx= Ax и поэтому можно писать dy = f(x)dx, т. е. производная равна отношению дифференциалов:

См. также Дифференциал.

Повторный дифференциал от dy имеет вид и вторым дифференциалом является значение d (dy )при dx=dx.

продолжение Дифференциальное исчесление.

Д. и. функций многих переменных. Для простоты рассматривается случай функций двух переменных (за нек-рым исключением), хотя все понятия легко распространяются на случай трех и большего числа переменных. Пусть функция z=f(x, у )задана в нек-рой окрестности точки ( х ₀, у ₀ )и пусть зафиксировано значение y=y₀. Тогда f(x, y₀ )есть функция только от х. Если она имеет в х ₀ производную по х, то эта производная наз. частной производной функции f( х, у) по х в точке ( х ₀, у ₀ )и обозначается f’x( х ₀, у ₀)> Итак, по определению,

где D_xz=f(x₀+Dx, y₀)-f(x₀, y₀) — частное приращение функции по х(dz/dx в общем случае нельзя рассматривать как дробь; д/дх есть символ операции).

Аналогично определяется частная производная по у:

(где, как и в случае одного переменного, dx=Dx, dy=Dyозначают приращения независимых переменных).

Первые частные производные =f’_x( х, у) и =f’_y(x, у), или частные производные первого порядка, являясь функциями от x и у, могут в свою очередь иметь частные производные по хи у, к-рые называются, по отношению к функции z=f(x, у), частными производными второго порядка, или вторыми частными производными. При этом полагают

Вместо d 2 z/dx 2 употребляют также обозначения

вместо д 2 z/дхду— обозначения

Каждой частной производной отвечает нек-рый частный дифференциал, получаемый умножением ее на дифференциалы независимых переменных, взятые в степенях, равных числу дифференцирований по соответствующему переменному. Так получаются п-е частные дифференциалы, или частные дифференциалы n-го порядка:

Справедлива следующая важная теорема о смешанных производных: если в нек-рой окрестности точки ( х ₀, у ₀ )функция z=f(x, у )имеет смешанные частные производные f»_xy(x, у )и f»_yx(x, у )и эти производные непрерывны в точке ( х ₀, у ₀), то f»_xy ( х ₀, у ₀) = f»_yx( х ₀, у ₀).

Функция z=f(x, у )наз. дифференцируемой в точке ( х ₀, у ₀ )по совокупности переменных х и у, если она определена в нек-рой окрестности этой точки и ее полное приращение

может быть представлено в виде

где Аи В— некоторые числа, w/r->0 при r= (при условии, что точка (x₀+ D х, у ₀+Dу)принадлежит упомянутой окрестности). При этом выражение

наз. полным дифференциалом (первого порядка) функции f(x, у )в точке ( х ₀, у ₀);это есть главная линейная часть приращения. Функция, дифференцируемая в точке, непрерывна в этой точке (обратное не всегда верно!). Более того, дифференцируемость влечет существование конечных частных производных

Таким образом, для функции, дифференцируемой ( х ₀, у ₀).

если, подобно случаю одного переменного, положим для независимых переменных dx=Dx, dy=Dy.

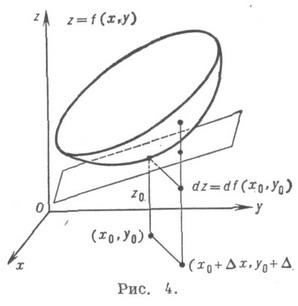
Существование конечных частных производных общем случае не влечет ее дифференцируемоcти (здесь нарушается аналогия с функциями одного переменного). Достаточный признак дифференцируемости функции двух переменных: если в нек-рой окрестности точки ( х ₀, у ₀ )функция f(x, у )имеет конечные частные производные f_x(x, у )и f’_y(x, y), непрерывные в точке ( х ₀, у ₀), то f дифференцируема в этой точке. Геометрически полный дифференциал df(x₀, y₀ )есть приращение аппликаты касательной плоскости к поверхности z=f(x,y )в точке (х ₀, у ₀, z₀), где z₀=f( х ₀, у ₀ )(см. рис. 4).

Полные дифференциалы высших порядков, подобно случаю функций одного переменного, вводятся по индукции равенством

в предположении, что дифференциал d n-1 z определе в нек-рой окрестности рассматриваемой точки и что приращения аргументов dx, dy берутся одни и те же на всех шагах. Аналогично определяются и повторные дифференциалы.

Тогда справедливы следующие теоремы:

Д. и. применяется к изучению свойств функций многих переменных: к отысканию экстремумов, к исследованию функций, задаваемых одним или несколькими неявными уравнениями, к теории поверхностей и т. д. Одним из главных инструментов при этом является Тейлора формула.

Понятия производной и дифференциала и их простейшие свойства, связанные с арифметич. действиями над функциями и суперпозицией функций, включая свойство инвариантности первого дифференциала, почти без изменений распространяются на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе понятия производной и дифференциала распространяются на функции точки абстрактного пространства.

Источник

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ, раздел математики, в к-ром изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную матем. дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 в.). Они сформулировали осн. положения Д. я. и чётко указали на взаимно обратный характер операций дифференцирования и интегрирования. С этого времени Д. и. развивается в тесной связи с интегральным исчислением, вместе с к-рым оно составляет осн. часть матем. анализа (или анализа бесконечно малых). Создание дифференциального и интегрального исчислений открыло новую эпоху в развитии математики. Оно повлекло за собой появление ряда матем. дисциплин: теорий рядов, теории дифференциальных уравнений, дифференциальной геометрии и вариационного исчисления. Методы матем. анализа нашли применение во всех разделах математики. Неизмеримо расширилась область приложений математики к вопросам естествознания и техники. «Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только с о-стояния, но и процессы: движение» (Энгельс Ф., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20, с. 587).

Это выражение при неограниченном уменьшении промежутка времени Дt приближается к величине gt, к-рую называют скоростью движения в момент времени t. Таким образом, скорость движения в к.-л. момент времени определяется как предел средней скорости, когда промежуток времени неограниченно уменьшается.

Осн. преимущество скорости в данный момент времени, или мгновенной скорости, перед средней скоростью состоит в том, что она, как и закон движения, является функцией времени t, а не функцией интервала (f,t + Дt). С другой стороны, мгновенная скорость представляет собой некоторую абстракцию, поскольку непосредственному измерению поддаётся средняя, а не мгновенная скорость.

Если производная f‘(x), в свою очередь, имеет производную, то её называют второй производной функции у = f(x) и обозначают

или D 2 f(x). Для прямолинейно движущейся точки вторая производная характеризует её ускорение.

Дифференциал. Функция у = f(x), область определения к-рой содержит нек-рую окрестность точки х₀, наз. дифференцируемой в точке х₀, если её приращение

Рассматриваются также дифференциалы высших порядков. На практике с помощью дифференциалов часто производят приближённые вычисления значений функции, а также оценивают погрешности вычислений. Пусть, напр., надо вычислить значение функции f(x) в точке х, если известны f(xo) и f‘(xo). Заменяя приращение функции её дифференциалом, получают приближённое равенство f(x₁)

Погрешность этого равенства приближённо равна половине второго дифференциала функции, т. е.

Исследование функций при помощи производных составляет основное приложение Д. и. Кроме того, Д. и. позволяет вычислять различного рода пределы функций, в частности пределы вида О/С и БЕСКОНЕЧНОСТЬ/БЕСКОНЕЧНОСТЬ (см. Неопределённое выражение, Лопиталя правило). Д. и. особенно удобно для исследования элементарных функций, т. к. в этом случае их производные выписываются в явной форме.

Аналогично определяется и обозначается частная производная z по у. Величина

Геометрически дифференцируемость функции двух переменных означает существование у её графика касательной плоскости, а дифференциал представляет собой приращение аппликаты касательной плоскости, когда независимые переменные получают приращения dx и dy. Для функции двух переменных понятие дифференциала является значительно более важным и естественным, чем понятие частных производных. В отличие от функций одного переменного, для функций двух переменных существование обеих частных производных первого порядка ещё не гарантирует дифференцируемости функции. Однако, если частные производные кроме того ещё непрерывны, то функция дифференцируема.

Историческая справка. Отдельные задачи об определении касательных к кривым и о нахождении максимальных и минимальных значений переменных величин были решены ещё математиками Древней Греции. Напр., были найдены способы построения касательных к коническим сечениям и нек-рым другим кривым. Однако разработанные античными математиками методы были применимы лишь в весьма частных случаях и далеки от идей Д. и.

В сер. 70-х гг. 17 в. Г. Лейбниц разработал очень удобный алгоритм Д. и. Осн. понятиями у Лейбница явились дифференциал как бесконечно малое приращение переменного и определённый интеграл как сумма бесконечно большого числа дифференциалов. Лейбницу принадлежат обозначения дифференциала dx и интеграла ИНТЕГРАЛ (ydx), ряд правил дифференцирования, удобная и гибкая символика и, наконец, сам термин «дифференциальное исчисление». Дальнейшее развитие Д. и. шло сначала по пути, намеченному Лейбницем; большую роль на этом этапе сыграли работы братьев Я. и И. Бернулли, Б. Тейлора и др.

История-Вилейтнер Г., История математики от Декарта до середины 19 столетия, пер. с нем., 2 изд., М., 1966; Строик Д. Я., Краткий очерк истории математики, пер. с нем., 2 изд., М., 1969; Cantor М., Vorlesungen uber Geschichte der Mathematik, 2 Aufl., Bd 3-4, Lpz.- В., 1901-24.

Работы основоположников и классиков Д. и. Ньютон И., Математические работы, пер. с латин., М.- Л., 1937; Леибниц Г., Избранные отрывки из математических сочинений, пер. с латин., «Успехи математических наук», 1948, т. 3, в. 1; Л‘Опиталь Г. Ф. де, Анализ бесконечно малых, пер. с франц., М.-Л-, 1935; Эйлер Л., Введение в анализ бесконечных, пер. с латин., 2 изд., т. 1, М., 1961; его же, Дифференциальное исчисление, пер. с латин., М.- Л., 1949; Коши О. Л., Краткое изложение уроков о дифференциальном и интегральном исчислении, пер. с франц., СПБ, 1831; его же, Алгебраический анализ, пер. с франц., Лейпциг, 1864.

Источник

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

— раздел математики, в к-ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу математич. анализа, имеющего чрезвычайное значение для естествознания и техники. Основной предпосылкой для создания Д. и. явилось введение в математику переменных величин (Р. Декарт, R. Descartes). В общих чертах построение дифференциального и интегрального исчислений было завершено в трудах И. Ньютона (I. Newton) и Г. Лейбница (G. Leibniz) к концу 17 в., однако вопросы обоснования с помощью понятия пре-

Производная. Пусть функция y=f(x). определена в нек-рой окрестности точки х ₀,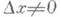есть приращение аргумента, Dy=f(x₀+Dx)-f(x₀).— соответствующее приращение функции. Если существует (конечный или бесконечный) предел

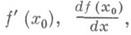
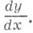
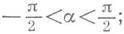
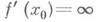
то он наз. производной функции f(x). в точке х ₀ и обозначается у’, у’ _х, Итак, по определению,

в случае касательная образует с Ох прямой угол (см. рис. 2). Таким образом, производная непрерывной функции f(x)в точке х ₀ совпадает с угловым коэффициентом tga касательной к кривой, заданной уравнением у=f(x), в ее точке с абсциссой х ₀.

Механичес кое истолков а ние производной. Пусть точка Мдвижется прямолинейно по закону s=f(t). За время Dt точка Мсместится на Ds=f(t+Dt)-f(t). Отношение Ds/Dt представляет собой среднюю скорость u _ср точки за время Dt. При неравномерном движении u_cp не постоянна. Мгновенной скоростью в момент tназ. предел средней скорости при т. е. u=f’(t). (в предположении, что эта производная существует).

Таким образом, понятие производной доставляет общее решение задачи о построении касательной к плоской кривой и задачи о вычислении скорости прямолинейного движения. Эти две задачи явились основными предпосылками в формировании понятия производной.

Функция, имеющая в точке х ₀ конечную производную, непрерывна в этой точке. В случае бесконечной производной этого может не быть. Непрерывная функция может не иметь ни конечной, ни бесконечной производной. Существуют непрерывные функции, не имеющие производной ни в одной точке области определения. Для производных основных элементарных функций справедливы следующие формулы (в любой точке области определения; исключения оговариваются):

Имеют место также следующие правила дифференцирования;

1) Если функции и(х)и u(х)дифференцируемы в точке х ₀, то функции

также дифференцируемы в этой точке, причем

2) Теорема о производной сложной функции: если функция y=f(u)дифференцируема в точке и ₀, а функция j(х)дифференцируема в точке х ₀, причем u₀=j(x_o), то сложная функция y-f(j(x))дифференцируема в точке х ₀ и y’_x=f(u₀)j'(x₀) или, в другой записи,

3) Теорема о производной обратнойфункции: если y=f(x)и x=g(y)- две взаимно обратные возрастающие (или убывающие) функции, заданные на нек-рых интервалах, и существует конечная производная то в точке y₀=f(z₀ )существует конечная производная или, в другой записи, Эта теорема допускает обобщение: если, при выполнении прочих условий, f’ (x₀) =0(f’ ( х _о)=), то g’( у _о)= (соответственно g’( у ₀)=0).

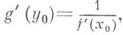
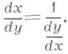
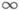
Односторонние производные. Если в точке х ₀ существует предел

Функция f(x)имеет производную в точке х ₀ в том и только в том случае, если в этой точке существуют равные между собой правая и левая производные. Для непрерывной функции существование в точке правой (соответственно левой) производной равносильно существованию в соответствующей точке ее графика правой (соответственно левой) односторонней полукасательной с угловым коэффициентом, равным значению этой односторонней производной. Точки, в к-рых полукасательные не образуют одну прямую, называются угловыми точками (см. рис. 3).

Функция y=f(x)имеет в точке хдифференциал в том и только в том случае, если она имеет в этой точке конечную производную

Функция, для к-рой существует дифференциал, наз. дифференцируемой в рассматриваемой точке. Таким образом, дифференцируем ость функции означает одновременно и существование дифференциала, и существование конечной производной. При этом dy = df(x)=f’(x)Ax. Для независимого переменного хполагают dx= Ax и поэтому можно писать dy = f(x)dx, т. е. производная равна отношению дифференциалов:

См. также Дифференциал.

Повторный дифференциал от dy имеет вид 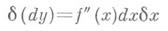и вторым дифференциалом является значение d (dy )при dx=dx.

продолжение Дифференциальное исчесление.

Д. и. функций многих переменных. Для простоты рассматривается случай функций двух переменных (за нек-рым исключением), хотя все понятия легко распространяются на случай трех и большего числа переменных. Пусть функция z=f(x, у )задана в нек-рой окрестности точки ( х ₀, у ₀ )и пусть зафиксировано значение y=y₀. Тогда f(x, y₀ )есть функция только от х. Если она имеет в х ₀ производную по х, то эта производная наз. частной производной функции f( х, у) по х в точке ( х ₀, у ₀ )и обозначается f’x( х ₀, у ₀)>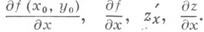Итак, по определению,

где D_xz=f(x₀+Dx, y₀)-f(x₀, y₀) — частное приращение функции по х(dz/dx в общем случае нельзя рассматривать как дробь; д/дх есть символ операции).

Аналогично определяется частная производная по у:

(где, как и в случае одного переменного, dx=Dx, dy=Dyозначают приращения независимых переменных).

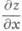
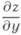
Первые частные производные =f’_x( х, у) и =f’_y(x, у), или частные производные первого порядка, являясь функциями от x и у, могут в свою очередь иметь частные производные по хи у, к-рые называются, по отношению к функции z=f(x, у), частными производными второго порядка, или вторыми частными производными. При этом полагают

Вместо d 2 z/dx 2 употребляют также обозначения

вместо д 2 z/дхду— обозначения

Каждой частной производной отвечает нек-рый частный дифференциал, получаемый умножением ее на дифференциалы независимых переменных, взятые в степенях, равных числу дифференцирований по соответствующему переменному. Так получаются п-е частные дифференциалы, или частные дифференциалы n-го порядка:

Справедлива следующая важная теорема о смешанных производных: если в нек-рой окрестности точки ( х ₀, у ₀ )функция z=f(x, у )имеет смешанные частные производные f»_xy(x, у )и f»_yx(x, у )и эти производные непрерывны в точке ( х ₀, у ₀), то f»_xy ( х ₀, у ₀) = f»_yx( х ₀, у ₀).

Функция z=f(x, у )наз. дифференцируемой в точке ( х ₀, у ₀ )по совокупности переменных х и у, если она определена в нек-рой окрестности этой точки и ее полное приращение

может быть представлено в виде

где Аи В— некоторые числа, w/r->0 при r= 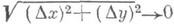(при условии, что точка (x₀+ D х, у ₀+Dу)принадлежит упомянутой окрестности). При этом выражение

наз. полным дифференциалом (первого порядка) функции f(x, у )в точке ( х ₀, у ₀);это есть главная линейная часть приращения. Функция, дифференцируемая в точке, непрерывна в этой точке (обратное не всегда верно!). Более того, дифференцируемость влечет существование конечных частных производных

Таким образом, для функции, дифференцируемой ( х ₀, у ₀).

если, подобно случаю одного переменного, положим для независимых переменных dx=Dx, dy=Dy.

Существование конечных частных производных общем случае не влечет ее дифференцируемоcти (здесь нарушается аналогия с функциями одного переменного). Достаточный признак дифференцируемости функции двух переменных: если в нек-рой окрестности точки ( х ₀, у ₀ )функция f(x, у )имеет конечные частные производные f_x(x, у )и f’_y(x, y), непрерывные в точке ( х ₀, у ₀), то f дифференцируема в этой точке. Геометрически полный дифференциал df(x₀, y₀ )есть приращение аппликаты касательной плоскости к поверхности z=f(x,y )в точке (х ₀, у ₀, z₀), где z₀=f( х ₀, у ₀ )(см. рис. 4).

Полные дифференциалы высших порядков, подобно случаю функций одного переменного, вводятся по индукции равенством

в предположении, что дифференциал d n-1 z определе в нек-рой окрестности рассматриваемой точки и что приращения аргументов dx, dy берутся одни и те же на всех шагах. Аналогично определяются и повторные дифференциалы.

Тогда справедливы следующие теоремы:

Д. и. применяется к изучению свойств функций многих переменных: к отысканию экстремумов, к исследованию функций, задаваемых одним или несколькими неявными уравнениями, к теории поверхностей и т. д. Одним из главных инструментов при этом является Тейлора формула.

Понятия производной и дифференциала и их простейшие свойства, связанные с арифметич. действиями над функциями и суперпозицией функций, включая свойство инвариантности первого дифференциала, почти без изменений распространяются на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе понятия производной и дифференциала распространяются на функции точки абстрактного пространства.

Источник