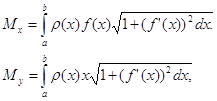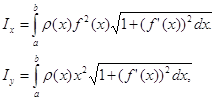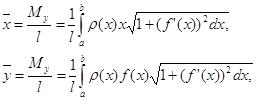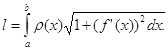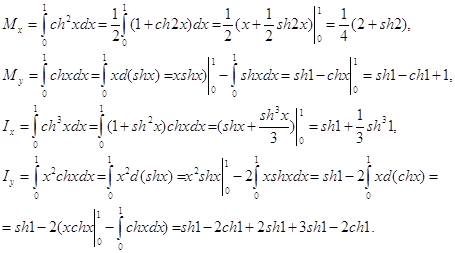что такое дифференциал в физике
Дифференциал в физике
2. Дифференциал в физике
Мы ввели понятие дифференциала с помощью равенства 
1. Работа. Найдем работу, которую совершает заданная сила F при перемещении по отрезку оси х. Если сила F постоянна, то работа А равна произведению F на длину пути. Если сила меняется, то ее можно рассматривать как функцию от х: F = F(x). Приращение работы А на отрезке [х, x+dx] нельзя точно вычислить как произведение F(x)dx, так как сила меняется, на этом отрезке. Однако при маленьких dx можно считать, что сила меняется незначительно и произведение представляет главную часть 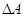
2. Заряд. Пусть q — заряд, переносимый электрическим током через поперечное сечение проводника за время t. Если сила тока / постоянна, то за время dt ток перенесет заряд, равный Idt. При силе тока, изменяющейся со временем по закону / = /(/), произведение I(t)dt дает главную часть приращения заряда на маленьком отрезке времени [/, t+-dt], т.е.- является дифференциалом заряда: dq = I 3. Масса тонкого стержня. Пусть имеется неоднородный тонкий стержень. Если ввести координаты так, как показано на рис. 130, то функция т= т(1) — масса куска стержня от точки О до точки /. Неоднородность стержня означает, что его линейная плотность не является постоянной, а зависит от положения точки / по некоторому закону р = р(/). Если на маленьком отрезке стержня [/, / + d/] предположить, что плотность постоянна и равна р(/), то произведение p(/)d/ дает дифференциал массы dm. Значит, линейная плотность — это производная массы по длине. 5. Снова работа. Рассмотрим работу как функцию времени. Нам известна характеристика работы, определяющая ее скорость по времени, — это мощность. При работе с постоянной мощностью N работа за время dt равна Ndt. Это выражение представляет дифференциал работы, т.е. dA = N(t)dt, и мощность выступает как производная работы по времени. Все приведенные примеры были построены по одному и тому знакомыми нам из курса физики: работа, перемещение, сила; заряд, время, сила тока; масса, длина, линейная плотность; и т. д. Каждый раз одна из этих величин выступала как коэффициент пропорциональности между дифференциалами двумя других, т. е. каждый раз появлялось соотношение вида dy = k(x)dx. На такое соотношение можно смотреть как на способ определения величины k(x). Тогда k(x) находится (или определяется) как производная у по х. Этот вывод мы и фиксировали в каждом примере. Возможна и обратная постановка вопроса: как найти зависимость у от х из заданного соотношения между их дифференциалами. 3. Приложения определенного интеграла к решению некоторых задач механики и физики 1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность моменты инерции IХ и Iу относительно тех же осей Ох и Оу вычисляются по формулам а координаты центра масс где l— масса дуги, т. е. Пример 1. Найти статические моменты и моменты инерции относительно осей Ох и Оу дуги цепной линии y=chx при 0≤x≤1. ◄ Имеем: В приложениях часто оказывается полезной следующая Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс. Пример 2. Найти координаты центра масс полуокружности ◄Вследствие симметрии Отсюда 1. Мат. Главная линейная часть приращения зависимой переменной величины (функции), приближенно выражающая значение этого приращения, а также приращение независимой переменной величины. 2. Тех. Механизм в автомобилях, тракторах, танках и т. п., позволяющий правому и левому ведущим колесам вращаться с различной скоростью. [От лат. differentia — разность] Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека Дифференциал (математика) — 1-форма, которая характеризует поведение функции в окрестности точки. Дифференциал (дифференциальная геометрия) Дифференциальное исчисление — раздел математического анализа. Дифференциалы высших порядков Дифференциал (механика) — часть трансмиссии, которая служит для того, чтобы ведущие колёса вращались не синхронно. Дифференциальный редуктор — один из классов механических редукторов. Дифференциальный диагноз — способ медицинской диагностики исключения возможности каких-либо заболеваний для сужения круга возможных. Дифференциальная защита — один из видов релейной защиты 1. матем. функционал, отражающий линейную часть приращения функции; обобщение производной 2. техн. автомоб. устройство, передающее вращение на два вала (в автомобиле — на ведущие колёса), но позволяющее им вращаться несинхронно ◆ Симметричный межколесный дифференциал в случае малого внутреннего трения распределяет крутящий момент поровну между полуосями. Кленников В. М., Кленников Е. В., «Теория и конструкция автомобиля», 2016 г. Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных. Насколько понятно значение слова ингуши (существительное): ДИФФЕРЕНЦИАЛ — • ДИФФЕРЕНЦИАЛ, в математике малое изменение величины в математическом выражении вследствие такого же незначительного изменения переменной. Если обозначить функцию х как f(x), то дифференциал функции, образующийся вследствие небольшого изменения… … Научно-технический энциклопедический словарь ДИФФЕРЕНЦИАЛ — (лат., от differe различать). Предел бесконечно малой разности между функцией переменного, получившего бесконечно малое приращение, и первоначальной функцией того же переменного (мат. терм.). Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка Дифференциал — премия или скидка по отношению к цене базисного сорта, с которыми могут быть предложены другие сорта, допустимые к поставке по фьючерсному контракту. Дифференциал компенсация дилеру за совершение сделки с нестандартной партией ценных бумаг. Дилер … Финансовый словарь Дифференциал — (математика) 1 форма, которая характеризует поведение функции в окрестности точки. Дифференциал (механика) часть трансмиссии, которая служит для того, чтобы ведущие колёса вращались не синхронно … Википедия ДИФФЕРЕНЦИАЛ — название дифференциального механизма в приводе ведущих колес автомобиля, трактора или других колесных машин. Наиболее распространен дифференциал с коническими зубчатыми колесами … Большой Энциклопедический словарь ДИФФЕРЕНЦИАЛ — (differential) Скорость изменения значения переменной на протяжении времени, которое считается непрерывной переменной. Скорость изменения переменной у, dy/dt, часто обозначается точкой над y(y ); d2y/dt2 обозначается двумя точками над y (ÿ), и т … Экономический словарь Дифференциал — А. Премия или скидка по отношению к цене базисного сорта, по которой могут быть предложены другие сорта, допустимые к поставке по фьючерсному контракту. Б. Компенсация дилеру за совершение сделки с нестандартным пакетом ценных бумаг. Словарь… … Словарь бизнес-терминов ДИФФЕРЕНЦИАЛ — (от латинского differentia разность, различие), одно из основных понятий дифференциального исчисления … Современная энциклопедия ДИФФЕРЕНЦИАЛ — (от лат. differentia разность различие), см. Дифференциальное исчисление … Большой Энциклопедический словарь ДИФФЕРЕНЦИАЛ — ДИФФЕРЕНЦИАЛ, а, муж. 1. В математике: линейная функция, приближенно равная нек рой функции в окрестности какой н. точки. Д. функции. 2. Механизм, дающий возможность расположенным на одной оси колёсам, вращающимся деталям двигаться с разной… … Толковый словарь Ожегова Еще раз. Сами по себе это две самостоятельные функции. Но, при использозовании действия «дифференцирования», одна из этих функций станет структурным элементом другой функции. Для чего это нужно? Для адекватного описания действительности. Потому, что почти все объекты действительного мира меняют свои размеры именно интегрированием. Схематичный пример действий дифференцирования и интегрирования расположен на рисунке в начале статьи. То есть, на точку «надеваем» колечко на том же самом расстоянии, что и радиус самого колечка, потому, что мы интегируем площади колечек именно по дифференциалу длины того отезка, который называется радиусом. Надеваем все больше колечек, выполняя исходное обязательное условие: Радиус каждого очень тонкого колечка равен расстоянию от первоначальной точки (вершины «пирамидки») до этого колечка. Будем получать объем пирамидки, равный интегралу площади колечек по диференциалу радиуса. Я, надеюсь, схема понятна. Именно эта модель вынесена в заголовок моего блога. Теперь, вернемся к заявленной теме статьи. Что такое неопределенность «ноль, деленный на ноль» или что такое бесконечность? Это модели нашего разума, а не модели реальности. Если часть площади круга представить как кольцо, ограниченное внутренней окружностью и внешней, то площадь кольца и будет приращением функции площади круга. Расстояние можду этими двумя окружностями и будет приращением аргумента. Если площадь кольца начать мысленно сжимать, то есть устремить друг к другу внешнюю окружность к внутренней, то пределом площади такого кольца станут две окружности, расположенные рядом. То есть, между ними не «влезет» другая окружность. Это будет элементарное приращение площади круга. Что с радиусом? Его длина станет элементарной и будет находиться между двумя соседними точками. Это и будет элементарным приращением аргумента. Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия, Нет. Есть «малое» в смысле метода последовательных приближений: на одном шаге оно пренебрежимое, а на другом уже нет. И с точностью до атомных размеров можем, если будем приборы класса СЗМ и интерферометрию использовать. Проблема разве что температуру и вибрацию стабилизировать 🙂 Не встречал в физике таких фантазий. И наконец, для справки. Когда рассчитывают движение планет, рассматривают дифференциалы от их положений. Когда рассчитывают приливные силы, рассматривают дифференциальные объёмы тел. При этом для нужд численного расчёта применяются размеры конечных элементов порядка многих километров и тысяч километров. Никакой природой физических объектов эти размеры не обусловлены (а исключительно достаточностью для требуемой точности расчётов). Ales в сообщении #386800 писал(а): ага, доже экстремумы толком не поизучаешь Таки да. Вот про то, что второй дифференциал (который симметрическая билинейная форма на касательном пространстве: Есть ещё малое по сравнению с чем-то: у физически бесконечно тонкого стержня толщина пренебрежимо мала по сравнению с длиной. Умозрительно можно и до абсолютного нуля заморозить, а начнёшь делать, так сразу сталкиваешься с тем, что ничерта не выходит. На учебник сослаться? Верно: когда «рассчитывают», используют математику и весь её арсенал. Какого сорта доказательства? Не бывает «в физике». Бывает «в физике в реальности» и «в физике в матмодели». Причём в физике в реальности дифференциалов нет вообще. Там есть амперметры, спектрометры, усилители, ПЗС, и т. п. Ни один из них «дифференциала» не измеряет (разность измерять могут). Она конкретная не совершенно, а ровно настолько, насколько вы умеете отличать не карандаш от карандаша. И насколько вы продумали дефиницию этого умения. Обычно дефиниции, придуманные априорно, работают довольно хреново, так что их приходится подправлять апостериорно, после фактического исследования карандаша. Ну, при наличии кривых рук ни черта не выходит, но экспериментаторы люди ушлые и целеустремлённые, они из сопли на коленке такое скрутят, что всё выйдет. Зачем нам абсолютный ноль? А до 1 К заморозить карандаш не проблема. Может быть, и до 1 мК, и до 1 мкК можно. Прикол как раз в том, что несмотря на эти проблемы, дифуравнения описывают природу не криво, а прямо. То есть природа подчиняется дифуравнениям лучше, чем мы её можем проверить. Каждый раз, повышая точность измерений и расчётов, мы убеждаемся, что только приблизились к точному аналитическому решению дифуравнения, а не отдалились от него. С этими фразами согласен, а вот раскрыть их вам не удалось. Понятно. Сами вы в лабораторию не заходили, а на какой-то отдельный учебник молитесь как на непререкаемую истину. Это даже можно усилить до общефилософского: любые свойства объектов познаются лишь в отношениях между ними. На самом деле происходит ровно наоборот: достаточно повысив точность, мы убеждаемся наконец, что уравнение мы вообще не то написали, кучу факторов не учли. Ну зачем так, в разделе для преподов, а не детей? (а я тут на своём месте, ибо 10 лет педстажа). Тут имелась в виду просто квадратичная форма, не дифференциальная внешняя форма. Мне это как раз и не нравится: одинаковые термины и обозначения используются для разных приемов, Интересно, вы не знаете никаких множеств чисел, кроме рациональных и вещественных? Не ожидал от вас подобного. Можно пользоваться понятием площади 🙂 Отсюда видно, что «бесконечно малой величиной» (по Сивухину) называется не «предельно малая длина, которую, ещё кое-как можно прочувствовать», а как раз наоборот, достаточно большая длина, чтобы не возникало ухудшения точности из-за её уменьшения. Таким образом, ту бессвязицу, которую вы нагородили, именно вы придумали. Сваливать её на других нехорошо. Ответ на засыпку: кривым что-то может быть абсолютно, а не по отношению к чему-то прямому. Это изучают в разделе дифференциальной геометрии, который называется «внутренняя дифференциальная геометрия», в отличие от «внешней». В теории тяготения можно ввести плоский фон, относительно которого искривлено пространство-время, но этот фон в ОТО оказывается ненаблюдаемым, как калибровка. Если бы вы назвали, из чего ещё, это звучало бы более веско. Так сплеча именно вы уничтожите физику как науку, объявляя математическое описание бессодержательным. К счастью, к такому мнению с начала 20 века не прислушиваются. Мало ли какие глупости были выдуманы Кантом или кем-нибудь ещё. Мистика действует отравляюще на мышление, а если её изгнать, реальность вполне остаётся, что было неоднократно проверено. Да, переход от одного уравнения к другому происходит. Но внимание: не происходит перехода от дифуравнения к чему-то другому. Новое описание снова является дифуравнением с тем же дифференцированием по действительно-числовым параметрам. paha в сообщении #387001 писал(а): А не подскажите литературу по симметрическим дифференциальным формам? я заглянул в АКартана. и мне вспомнилась моя давняя мечта. которую я пытался воплотить на третий (sic!) год преподавания, да и еще на неподходящем потоке. уже начал переводить в буквы. вот начало под оффтопом \section<Производные отображений аффинных пространств> Отображение Нетрудно видеть, что такое отображение <\it единственно>, что видно из оценки Второе производное отображение для Отсюда видно, что «бесконечно малой величиной» (по Сивухину) называется не «предельно малая длина, которую, ещё кое-как можно прочувствовать», а как раз наоборот, достаточно большая длина, чтобы не возникало ухудшения точности из-за её уменьшения. Таким образом, ту бессвязицу, которую вы нагородили, именно вы придумали. Сваливать её на других нехорошо. Ясно. Вот Логунов говорил, что таки наблюдаемо, но я не интересовался его обоснованиями этого. Если мы возьмём определение мистики из словаря, то и Ваши, и мои слова совсем потеряют смысл. Ой, да нет же. Принято. paha в сообщении #387001 писал(а): А не подскажите литературу по симметрическим дифференциальным формам? Я понял, что не про дифформы была речь, а спросил именно про дифформы типа метрического тензора. Вот и тонем, когда надо мелочь какую-нибудь найти. Сейчас этот форум просматривают: нет зарегистрированных пользователей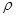

Значение слова «дифференциал»
дифференциа́л
Делаем Карту слов лучше вместе

Дифференциал
Полезное
Смотреть что такое «Дифференциал» в других словарях:

У ДВУХ математических действий дифференцирования: по частному и по полному дифференциалам
должны быть и ДВА обратных действия интегрирования: с константой интегрирования и без константы!
Научный форум dxdy
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные наукиЧто такое дифференциал?
Заслуженный участник Заслуженный участник Заслуженный участник
Тем более, что от второго дифференциала никакого толку,




Заслуженный участник
У Сивухина целый параграф про смысл производной и интеграла, и есть ещё очень важный абзац ближе к началу о границе между физикой и математикой.
Лучшего изложения этого места я лично нигде не видел: разжёвано и в рот положено.
Прикол, кстати, даже в том, что сами дифуравнения описывают природу криво: там из-за погрешностей измерений по теореме Котельникова всё дискретно и надо было бы разностные уравнения-то писать, а не дифференциальные.
Просто математики и физики разные задачи решают: математикам нужно решить чётко поставленную задачу, а физикам эта чётко поставленная задача сама по себе не нужна, потому что чем она чётче поставлена, тем менее точно она Природе соответствует, а им понять нужно, что там твориться в исследуемой системе.
Знание границы между науками помогает не ошибиться: физикам не сосчитать что-то, что точное, но в данной задаче не нужно, а математикам не начать рассуждать с посылок, верность которых надёжно не установлена.
Зайдите в лабораторию к физикам и поспрашивайте, как они работают: например, что у них в формулах за 
На учебник уже сослался выше.Заслуженный участник Заслуженный участник Заслуженный участник
Если согласны с этим, то вот вопрос на засыпку: относительно чего тяготеющие тела искривляют вокруг себя пространство-время? (кривым что-то может же быть лишь по отношению к чему-то прямому).
Как раз из научной физлаборатории и вещаю, между прочим.
Но, опять же, если где-то в другой лаборатории или ВУЗе думают иначе, так это ж прекрасно: есть с чем сравнивать, а сравнение точек зрения их взаимообогащает.
возникает непонимание и путаница.Заслуженный участник Заслуженный участник
симметрическая билинейная форма на касательном пространствеЗаслуженный участник Заслуженный участник Заслуженный участник
Пусть 








Если 

<\it производным отображением>для 







(здесь использована каноническая структура аффинного пространства на векторном).Заслуженный участник
Не могу эту тему продолжить, так как она к дифференциалам не имеет отношения, да и лень.
Тоже уже очень далеко мы от дифференциалов-то уехали.
Физики раздражают математиков тем, что рассуждают очень не строго и используют понятия, которые сами редко умеют даже сформулировать, куда уж там определить.
Я то хотел сказать, что физики иначе не могут делать по простой причине.
Ну, уменьшайте мысленно размер системы, повышая точность измерения длины: на атомном уровне все классические дифуры улетучатся как дым.
Они ещё много раньше улетучатся: там мезоскопическая физика такая есть (совсем не разработанная, правда, наука такая).
Я тоже больно нежный стал.
симметрическая билинейная форма на касательном пространствеКто сейчас на конференции