что такое действительный показатель

1.1.7 Свойства степени с действительным показателем

Видеоурок 1: Степень с рациональным и действительным показателями. Часть 1

Видеоурок 2: Степень с рациональным и действительным показателями. Часть 2

Лекция: Свойства степени с действительным показателем

При рассмотрении степеней с действительным показателем в показателе может быть абсолютно любое значение, а, значит, при работе с такими степенями следует использовать следующие свойства.

Свойства степени с действительным показателем

Если в основании степени лежит положительное число, а в качестве показателя используются действительные числа, то можно пользоваться следующими формулами:

1. Так как в основании степени используется положительное число, то, несмотря на знак показателя степени, результат всегда будет числом положительным.

2. Если показатель степени является отрицательным числом, то его можно заменить на равный по модулю положительный показатель, а основание дроби перевернуть.

3. При умножении чисел с одинаковыми основаниями, действительные показатели степени следует сложить.

4. При делении чисел с одинаковыми основаниями, действительные показатели степени вычитаются:

5. При возведении числа в степени в дополнительную степень показатели умножаются.

7. При возведении частного некоторых чисел в действительную степень можно возвести каждое число по отдельности в данную дробь и только после этого разделить.

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №17. Степень с рациональным и действительным показателем.

Перечень вопросов, рассматриваемых в теме

2) определение степени с рациональным и действительным показателем;

3) нахождения значения степени с действительным показателем.

Если n- натуральное число, , m— целое число и частное является целым числом, то при справедливо равенство:

.

При любом действительном х и любом положительном а ) степень является положительным числом:

Но если основание степени а=0, то степень определяют только при и считают, что

При выражение не имеет смысла.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Пример: вычислим

Мы можем представить , тогда

Таким образом, мы можем записать

или

На основании данного примера можно сделать вывод:

Если n- натуральное число, , m— целое число и частное является целым числом, то при 0 справедливо равенство:

.

Таким образом, степень определена для любого рационального показателя r и любого положительного основания а.

Если , то выражение имеет смысл не только при 0, но и при а=0, причем, Поэтому считают, что при r0 выполняется равенство

Пользуясь формулой степень с рациональным показателем можно представить в виде корня и наоборот.

Рассмотрим несколько примеров:

Отметим, что все свойства степени с натуральным показателем, которые мы с вами повторили, верны для степени с любым рациональным показателем и положительным основанием, а именно, для любых рациональных чисел p и q и любых 0 и 0 ы следующие равенства:

Разберем несколько примеров, воспользовавшись данными свойствами:

В числителе вынесем общий множитель ab за скобки, в знаменателе представим корни в виде дробных показателей степени:

А теперь дадим определение степени с действительным показателем, на примере .

Пусть последовательность десятичных приближений с недостатком :

Эта последовательность стремится к числу , т.е.

Числа являются рациональными, и для них определены степени т.е. определена последовательность

Можно сделать вывод, что данная последовательность стремится к некоторому действительному числу, которое обозначают , т.е. .

Опредление степени с действительным показателем.

При любом действительном х и любом положительном а ) степень является положительным числом:

Но если основание степени а=0, то степень определяют только при и считают, что

При выражение не имеет смысла.

Для степени с действительным показателем сохраняются все известные свойства степени с рациональным показателем, из которых следует теорема.

Теорема. Пусть и . Тогда .

По условию . Поэтому, по свойству 1 имеем
а^(х₂). Умножив обе части этого равенства на положительное число , получим . По свойству умножения степеней получаем: , т.е. .

Из данной теоремы вытекают три следствия:

.

.

Эти теорема и следствия помогают при решении уравнений и неравенств, сравнении чисел.

Примеры и разборы решения заданий тренировочного модуля

Пример 1. Сравнить числа

Сравним показатели

Источник

Свойства степеней. Действия со степенями

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

a — основание степени

n — показатель степени

Соответственно, a n = a·a·a·a. ·a

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 — она решается довольно просто:

2 — основание степени

3 — показатель степени

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. В начале каждого года вы зарабатываете на нем еще два. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Источник

Лекция: Степень с рациональным и действительным показателями

Степень с рациональным и действительным показателями

Мы уже знакомы со степенями с натуральным показателем. Это числа вида: 2 3 , 6 2 и т.д. А что такое степени с рациональным и действительным показателем? Что у них общего и в чем их отличие от степеней с натуральным показателем?

Для начала повторим некоторые свойства степеней с натуральным показателем:

Степень с рациональным показателем.

Таким образом, можно записать = 125 =

Если n – натуральное число, n 2, m – целое число и частное является целым числом, то при a 0 справедливо равенство

Применяя свойства степени и арифметического корня, получаем

Если то выражение имеет смысл не только при a  0, но и при а = 0, причём

Поэтому считают, что при r  0 выполняется равенство

Пользуясь формулой (1), степень с рациональным показателем можно представить в виде корня и наоборот.

Можно показать, что все свойства степени с натуральным показателем верны для степени с любым рациональным показателем и положительным основанием.

А именно для любых рациональных чисел p и q и любых a  0 и b  0 верны равенства:

Степень с действительным показателем.

Источник

Степень числа: определения, обозначение, примеры

В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.

Степени с натуральными показателями: понятие квадрата и куба числа

Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).

Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.

Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.

Что такое степени с целым показателем

В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.

Степень числа с целым положительным показателем можно отобразить в виде формулы: .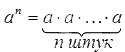

При этом n – любое целое положительное число.

Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:

Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0

При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.

Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).

Проиллюстрируем нашу мысль конкретными примерами:

В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:

Что такое степени с рациональным показателем

Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.

Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.

Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.

Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как

При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.

Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.

Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.

Объединим все данные выше определения в одной записи:

Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.

Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.

При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:

Что такое степени с иррациональным и действительным показателем

Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.

и так далее (при этом сами приближения являются рациональными числами).

Источник