что такое действительные значения переменной х
Действительные числа: определение, примеры, представления
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?
Данное определение можно записать иначе с учетом следующего:
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
Представления действительных чисел
Под определение дейситвительных чисел попадают:
Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.
Область определения функции
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
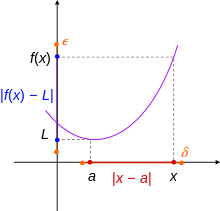
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Область определения степенной функции
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
Рассмотрим несколько примеров.
Область определения показательной функции
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Действительные числа
Определение действительных чисел
Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —
Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —
Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:
Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.
Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.
Примеры действительных чисел:
Число нуль также является действительным числом, так как 0 — рациональное число.
Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.
При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.
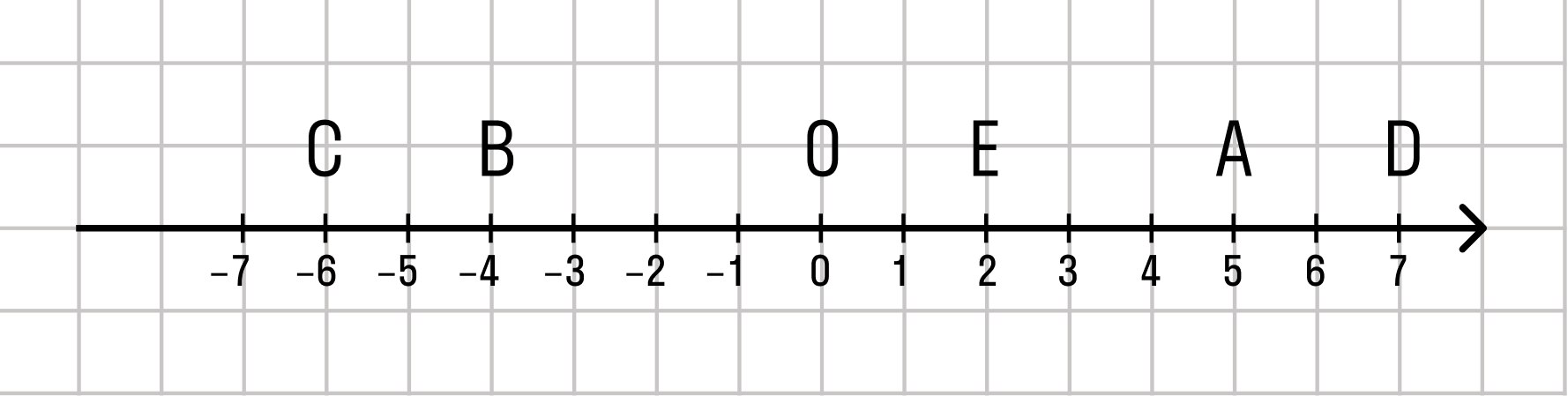
Действительные числа на координатной прямой
Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Интересный факт: действительные числа заполняют каждую точку координатной прямой.
Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.
Представления действительных чисел
По определению действительными числами являются:
Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.
Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений
будут действительные числа.
Сравнение действительных чисел
Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:















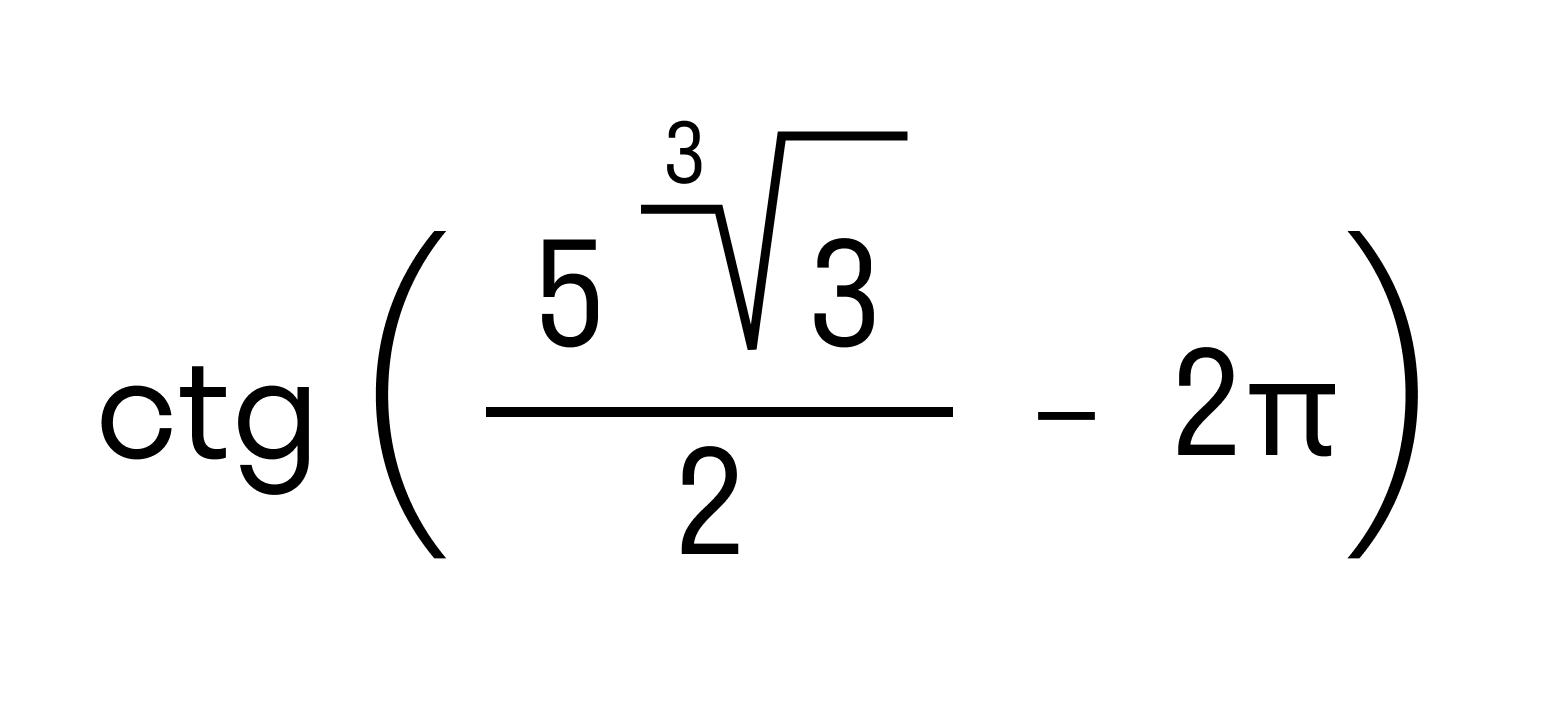



 .
.