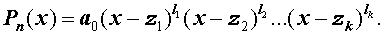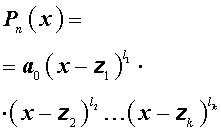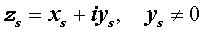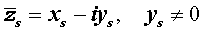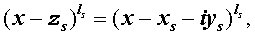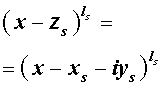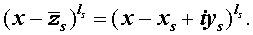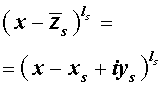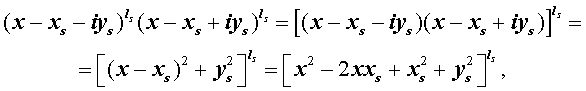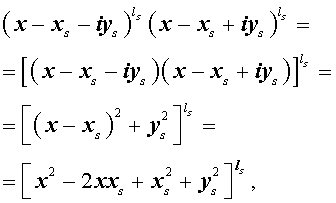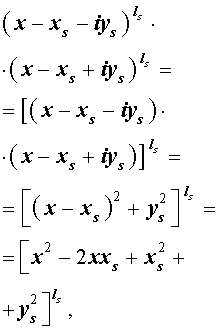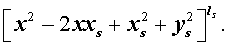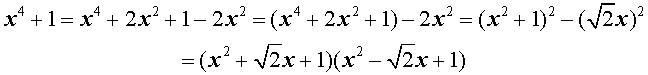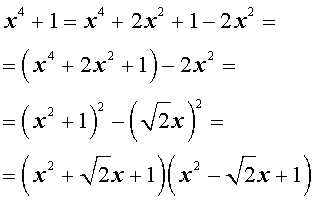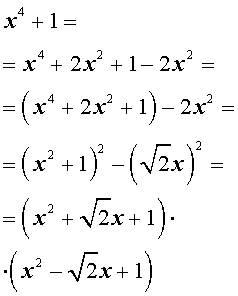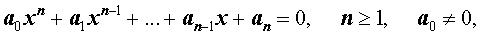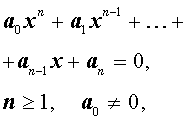что такое действительные коэффициенты

Основная теорема алгебры и ее следствия

Основная теорема алгебры. Всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.

Следствие 1. Любой многочлен степени 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADEAAAAQBAMAAABNQoq8AAAAKlBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHrpZrAAAADnRSTlMA/sAYMQXYQYWhYbFRcq20Ms4AAACTSURBVBjTY2AgETjgEGc+pIBDRm0iigzXYgSbEVXPsmZUGebdDpd0oFKTUWQ4nbILGg0gAocmI8uYMYkwHCyAihRNR5IxZ9zA0Ah3frUKkgscLzCkwa32RJZpdGCWgEkUbUd2tSIDr4g1VALFBQzSDEwJPVBXs0JlDEEyLFIMPJINqD5tFBQUB1JAvxiDQ6cZNfAAvaobxKduFrwAAAAASUVORK5CYII=» /> с комплексными коэффициентами можно представить в виде произведения линейных двучленов:

где — корни многочлена (могут быть комплексные).

Если комплексное число является корнем этого многочлена, то есть

Следствие 3. Если комплексное (но не действительное) число — корень многочлена с действительными коэффициентами, то сопряженное число является его корнем той же кратности.

Следствие 4. Всякий многочлен с действительными коэффициентами представляется в виде произведения линейных двучленов и квадратных трехчленов (с отрицательными дискриминантами):

Следствие 5. Многочлен нечетной степени с действительными коэффициентами всегда имеет хотя бы один действительный корень.

Многочлен четной степени с действительными коэффициентами может не иметь действительных корней (при этом в разложении (В. 14) отсутствуют линейные двучлены ).

Пример В.14. Многочлен

а) представить в виде (В.14);

б) представить в виде (В.13).

Решение. Данный многочлен имеет двойной корень и простой корень (см. пример В.13). Поэтому его можно представить в виде

Разделим многочлен на многочлен «уголком»:

б) разложим квадратный трехчлен на линейные множители, что возможно над полем комплексных чисел:

Тогда разложение (В. 13) для данного многочлена принимает вид

Источник

Разложение многочленов на множители. Формулы Виета

Алгебраические уравнения

Основная теорема алгебры. Разложение многочленов на линейные множители в комплексной области

Разложение на множители многочленов с действительными коэффициентами

Теорема (формулы) Виета

Алгебраические уравнения

Пусть n – произвольное натуральное число. Рассмотрим многочлен n – ой степени от переменной x

Заметим, что в этом случае коэффициент a₀ отличен от нуля, и введем следующее определение.

.

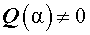
Разложение многочленов на множители в комплексной области

Основная теорема алгебры (теорема Гаусса) утверждает, что любое алгебраическое уравнение вида (3) имеет n корней, при условии, что каждый корень считается столько раз, какова его кратность.

– полный набор корней уравнения (3), а

– их кратности, то, во-первых,

а, во-вторых, справедливо равенство

Разложение на множители многочленов с действительными коэффициентами

Рассмотрим теперь многочлены степени 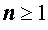, все коэффициенты которых являются вещественными числами.

Тогда справедливо следующее

является корнем кратности l_s многочлена с вещественными коэффициентами, то и комплексно сопряженное число

Из утверждения вытекает, что в разложение (4) степень каждого бинома, содержащая комплексный корень z_s и имеющая вид

входит в паре со степенью бинома, содержащей комплексно сопряженный корень 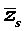и имеющей вид

то произведение каждой пары биномов (5) и (6), входящей в формулу (4), даёт степень квадратного трехчлена с вещественными коэффициентами:

Теорема (формулы) Виета

Снова рассмотрим уравнение n – ой степени от переменной x

и, немного изменив предыдущие обозначения, предположим, что

— его корни, причем в записи (8) каждый корень взят столько раз, какова его кратность.

Тогда из формулы (4) вытекают следующие равенства, которые называют формулами Виета для уравнения n – ой степени :

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №11. Многочлен P(x) и его корень. Алгебраическое уравнение.

Перечень вопросов, рассматриваемых в теме

1) обобщенное понятие многочлена;

2) основные действия над многочленами;

3) определение алгебраического уравнения;

Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).

Следствие. Если число а является корнем многочлена Р(х), то многочлен

где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнением над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Общая теория многочленов многих переменных далеко выходит за рамки школьного курса.

Мы рассмотрим многочлены одной действительной переменной, да и то в простейших случаях. Рассмотрим многочлены одной переменной, приведённые к стандартному виду.

Стоит отметить, что каждый многочлен степени больше 2 можно разложить на множители.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль.

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида

где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнением над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

является алгебраическим уравнением четвертой степени от трёх переменных (с тремя неизвестными) над множеством вещественных чисел.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов. В данной теореме алгебраические характеристики многочленов (они позволяют работать с многочленами как с целыми числами) связываются с их функциональными характеристиками (которые позволяют рассматривать многочлены как функции).

Теорема Безу. Остаток от деления многочлена Р(х) на двучлен х-а равен Р(а).

Эту закономерность отметил и математик Безу.

Следствие. Если число а является корнем многочлена Р(х), то многочлен

Основные работы Этьенна Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений.

В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках.

Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный «Курс математики», написанный им в 1764-69 годах.

Безу развил метод неопределённых множителей. В элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе.

Часть трудов Безу посвящена внешней баллистике.

Именем ученого названа одна из основных теорем алгебры.

Примеры алгебраических уравнений

Примеры и разбор решения заданий тренировочного модуля

Разложим на множители многочлен:

Решение: )

Ответ: ))

Источник

действительный коэффициент

Смотреть что такое «действительный коэффициент» в других словарях:

действительный коэффициент трансформации — Отношение действительного первичного к действительному вторичному напряжению. [IEV 321 01 18 измененный] [ГОСТ Р МЭК 60044 7 2010] EN actual transformation ratio of a voltage transformer the ratio of the actual primary voltage to the actual… … Справочник технического переводчика

действительный коэффициент полезного действия — tikrasis naudingumo koeficientas statusas T sritis radioelektronika atitikmenys: angl. actual efficiency vok. realer Wirkungsgrad, m rus. действительный коэффициент полезного действия, m pranc. rendement actuel, m … Radioelektronikos terminų žodynas

эффективный (действительный) коэффициент распространения пучка — 3.9 эффективный (действительный) коэффициент распространения пучка : Инвариантная величина, характеризующая фокусируемость астигматического пучка: (8) где det(P) детерминант (определитель) … Словарь-справочник терминов нормативно-технической документации

Коэффициент сжимаемости — отношение относительной вертикальной деформации (изменения коэффициента пористости) к давлению, вызвавшему эту деформацию. Источник: ГОСТ 30416 96: Грунты. Лабораторные испытания. Общие положения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Коэффициент операционных расходов — (EXPENSE RATIO) определяется путем деления величины стабильных операционных расходов на действительный валовой доход. * * * (OPERATING EXPENSE RATIO) отношение операционных расходов к потенциальному или действительному валовому доходу … Словарь инвестиционных и оценочных терминов

ГОСТ Р ИСО 11146-2-2008: Лазеры и лазерные установки (системы). Методы измерений ширин, углов расходимости и коэффициентов распространения лазерных пучков. Часть 2. Астигматические пучки — Терминология ГОСТ Р ИСО 11146 2 2008: Лазеры и лазерные установки (системы). Методы измерений ширин, углов расходимости и коэффициентов распространения лазерных пучков. Часть 2. Астигматические пучки оригинал документа: 3.4 вигнера распределение… … Словарь-справочник терминов нормативно-технической документации

Стабилитрон — У этого термина существуют и другие значения, см. Стабилитрон (значения) … Википедия

Погрешность — 10. Погрешность По title= РМГ 29 99 ГСИ. Метрология. Основные термины и определения Источник: ГОСТ 12.1.016 79: Система станд … Словарь-справочник терминов нормативно-технической документации

СТО 70238424.17.220.20.001-2011: Измерительные трансформаторы. Условия поставки. Нормы и требования — Терминология СТО 70238424.17.220.20.001 2011: Измерительные трансформаторы. Условия поставки. Нормы и требования: 3.1.13 класс точности трансформатора тока (напряжения) номинальный : Класс точности, гарантируемый трансформатору тока (напряжения)… … Словарь-справочник терминов нормативно-технической документации

actual efficiency — tikrasis naudingumo koeficientas statusas T sritis radioelektronika atitikmenys: angl. actual efficiency vok. realer Wirkungsgrad, m rus. действительный коэффициент полезного действия, m pranc. rendement actuel, m … Radioelektronikos terminų žodynas

realer Wirkungsgrad — tikrasis naudingumo koeficientas statusas T sritis radioelektronika atitikmenys: angl. actual efficiency vok. realer Wirkungsgrad, m rus. действительный коэффициент полезного действия, m pranc. rendement actuel, m … Radioelektronikos terminų žodynas

Источник

Большая Энциклопедия Нефти и Газа

Действительный коэффициент

Уравнение с действительными коэффициентами может иметь только попарно сопряженные комплексные корни. [31]

Многочлен с действительными коэффициентами в общем случае может иметь как действительные, так и комплексные корни. [33]

Многочлен с действительными коэффициентами всегда разлагается в произведение линейных и квадратичных множителей, коэффициенты которых также действительны. [35]

В этом случае действительный коэффициент усиления по мощности может быть значительно увеличен без изменения оптимального сопротивления нагрузки Ru, соответствующего максимуму выходной мощности, которую можно получить от данного дросселя насыщения. [36]

Конечно, если действительный коэффициент запаса прочности п значительно превышает требуемый ( допускаемый) [ п ], то результат расчета также не может считаться удовлетворительным, так как при этом конструкция неэкономична. [37]

Более точное значение действительного коэффициента преобразования может быть получено на основе термодинамического анализа обратного кругового процесса. [39]

Всякий многочлен с действительными коэффициентами может быть представлен в виде произведения линейных и квадратичных сомножителей, соответствующих действительным и комплексным корням. Многочлен разлагается на линейные множители тогда и только тогда, если все его корни действительные. [40]

Это уравнение с действительными коэффициентами и его решение значительно проще. [42]

Система уравнений с действительными коэффициентами и действительными неизвестными получается для цепей постоянного тока. [43]

Всякий многочлен с действительными коэффициентами может быть представлен в виде произведения линейных и квадратичных сомножителей, соответствующих действительным и комплексным корням. Многочлен разлагается на линейные множители тогда и только тогда, если все его корни действительные. [44]

Источник