что такое дерево проблем
СТРОИМ «ДЕРЕВО ПРОБЛЕМ»
СТРОИМ «ДЕРЕВО ПРОБЛЕМ»
Теоретические знания вы уже получили, теперь можно приступать к построению «дерева».
• Для начала произвольно выбираем одну или несколько проблем.
• Затем снимаем по одной карточке с проблемами и пробуем выстроить между ней и уже размещенными карточками-проблемами причинно-следственную связь. Если две проблемы не связаны между собой – разместите их рядом. Если одна проблема явно является причиной другой (пусть не очевидно, но все же связанной с ней) проблемы – опустите ее ниже, если следствием – поднимите выше.
• Если логическая связь не очевидна, попробуйте сформулировать и добавить между причиной и следствием еще одну карточку-проблему, с появлением которой связь станет ясна.
• Если вы видите, что проблема «не подходит» – временно отложите ее в сторону.
• Карточки еще не закончились? Берите следующую карточку-проблему и поступайте с ней по описанному алгоритму.
• Если проблемы закончились – выберите одну из «ветвей» и попробуйте рассмотреть вопрос более детально: поискать «причины причин» или «следствия следствий». Задайте вопрос: «А только ли эти две (три, четыре…) причины являются основными для данного следствия? Есть ли еще другие?» Добавьте недостающие.
Постепенно ваше «дерево» будет обрастать «кроной», а «корневая система» укрепляться, добавляя все новые и новые «корни».
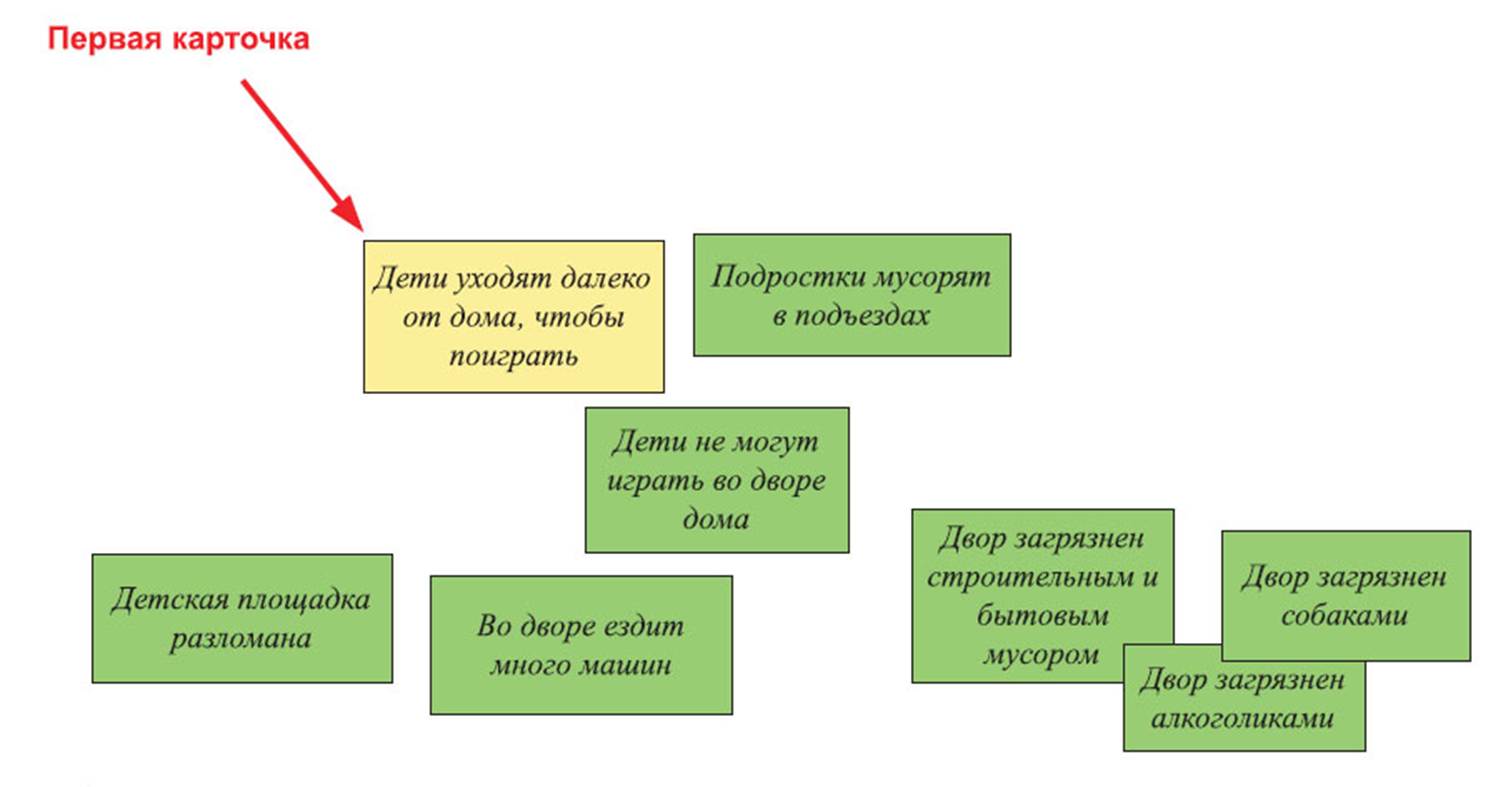
Для нашего примера картинка будет примерно такой, как показано на Рисунке 9. Пример результата подготовки к построению «дерева проблем». Попробуем предположить, как в этом случае шел бы ход обсуждения.
Сначала могли взять слово «разгневанные сложившейся ситуацией родители»:
Рисунок 7. Подготовка к построению «дерева проблем» – шаг 1
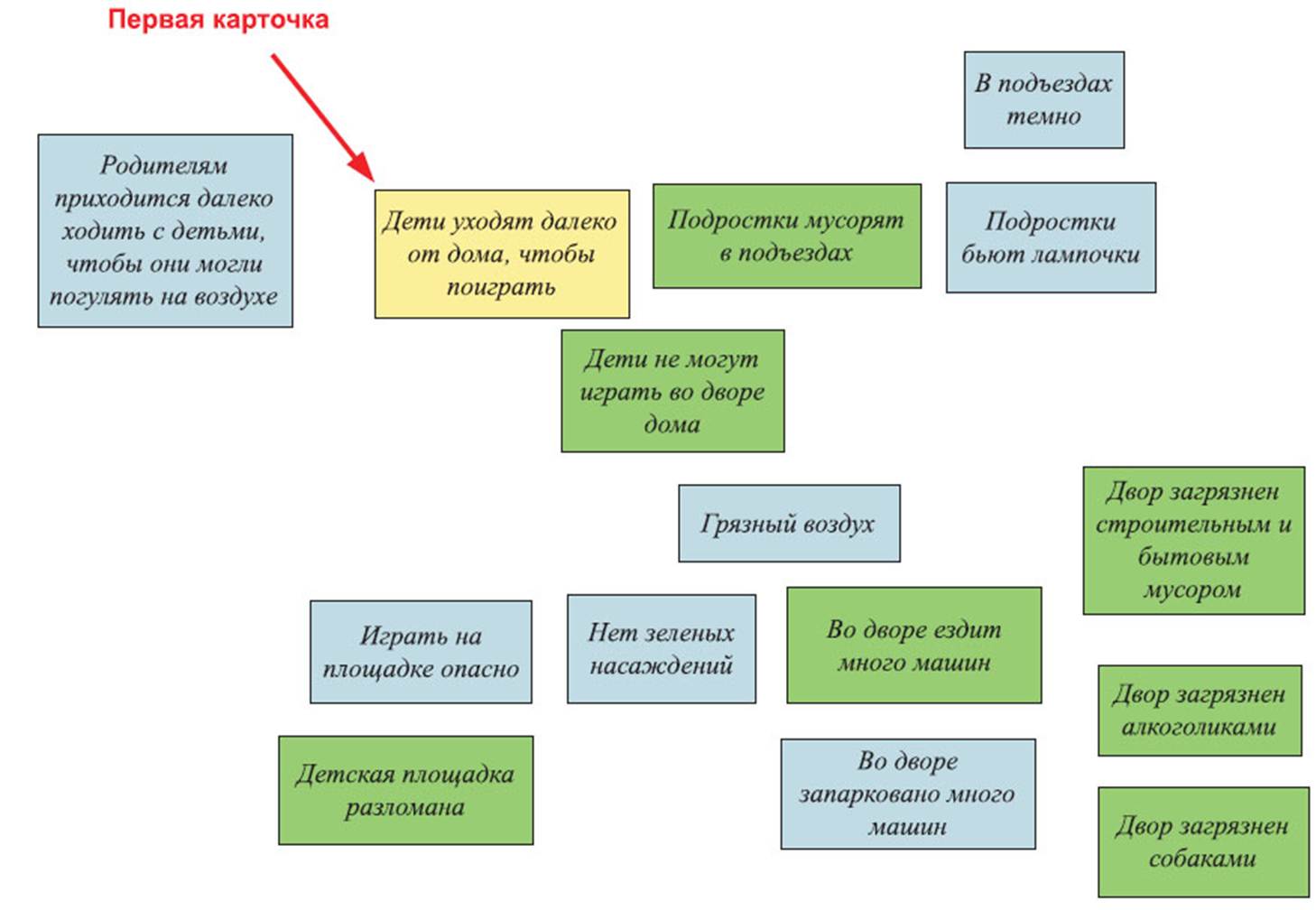
Далее подключаются «бездетные» жильцы и пенсионеры, ход обсуждения мог пойти таким образом:
Рисунок 8. Подготовка к построению «дерева проблем» – шаг 2
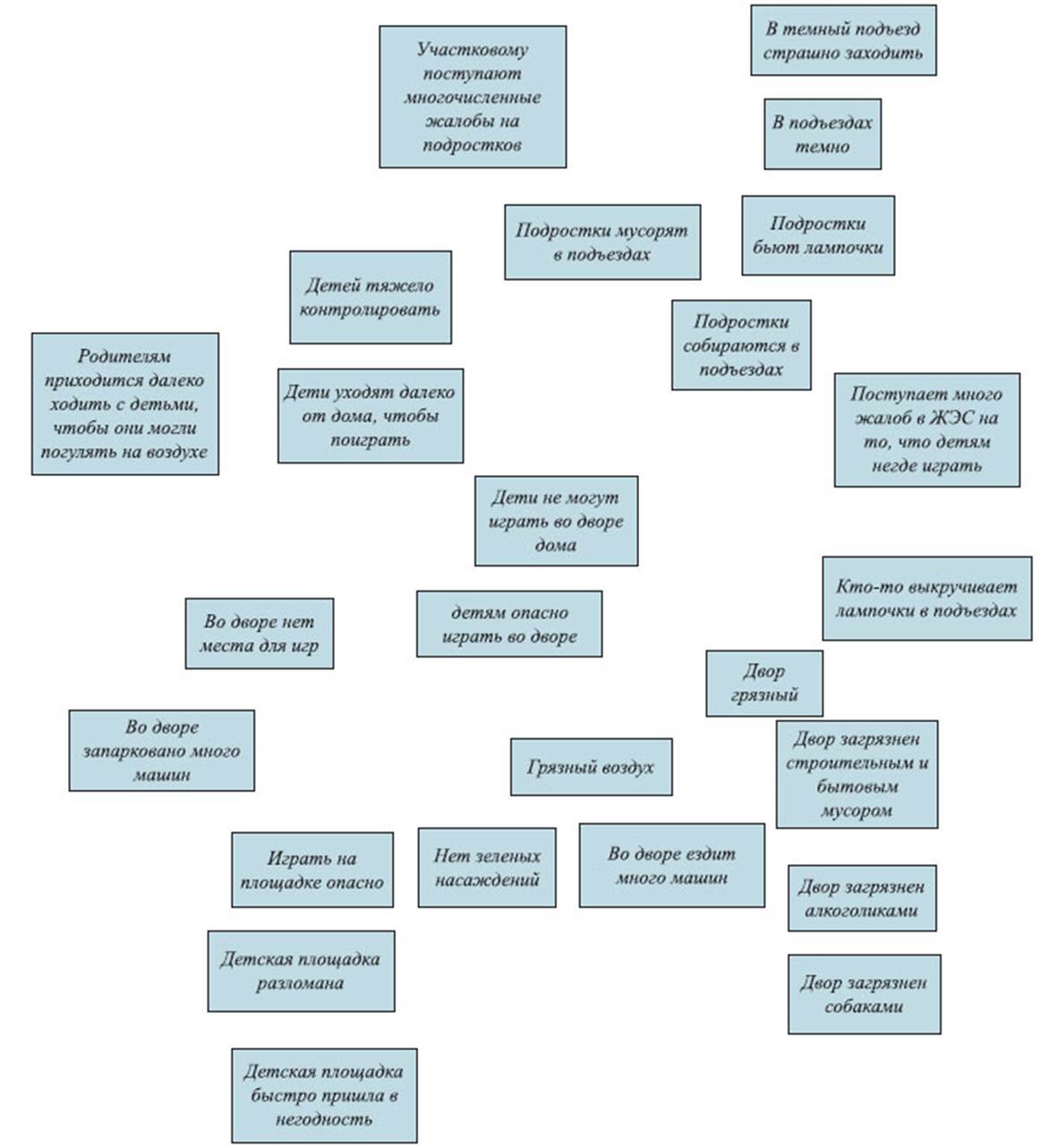
После окончательного размещения проблем, картина примет такой вид (см. Рисунок 9.):
Рисунок 9. Пример результата подготовки к построению «дерева проблем»
Теперь осталось только прорисовать причинно-следственные связи.
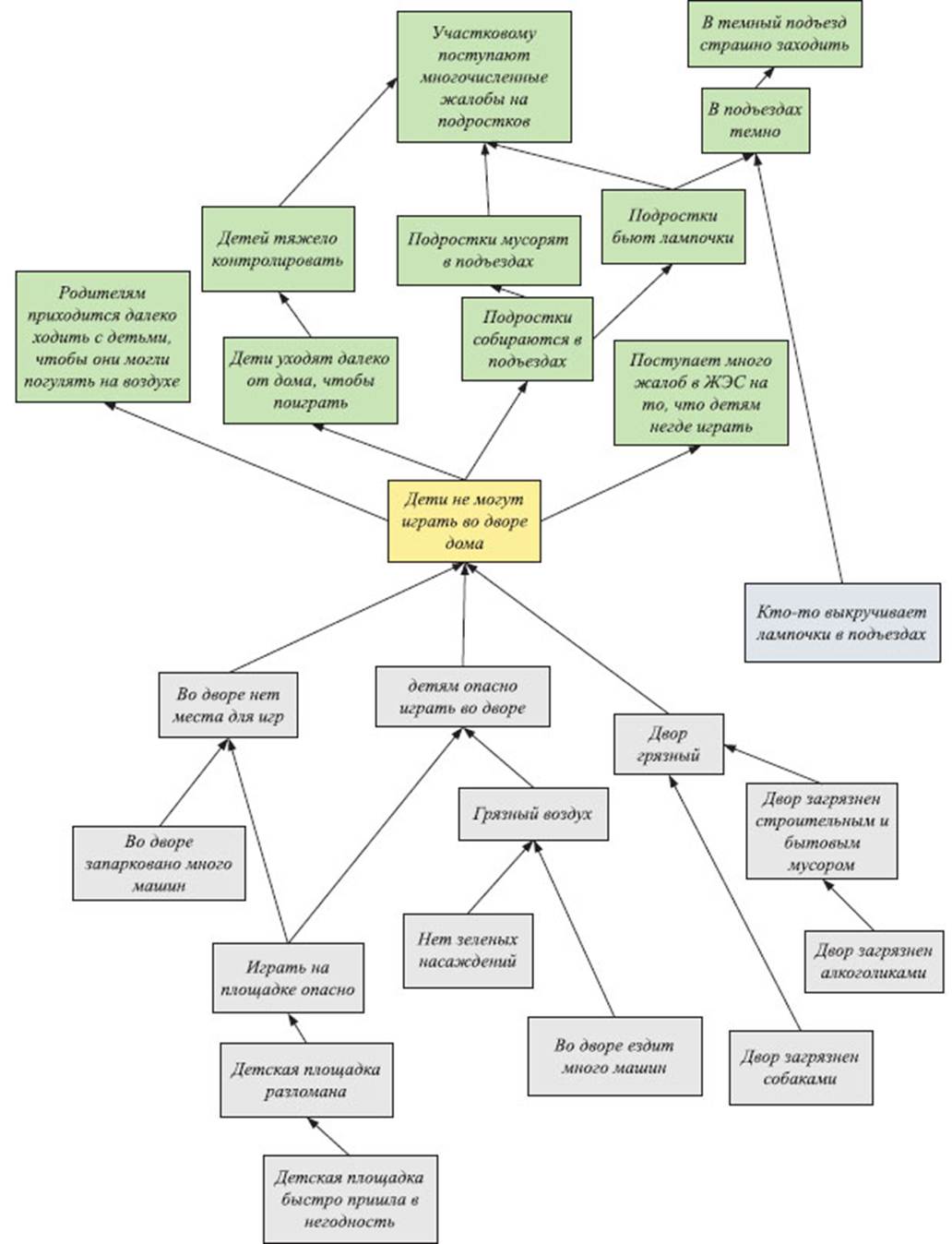
После их прорисовки и некоторой оптимизации схемы (передвинуты некоторые карточки с причинами и следствиями) в нашем примере, дерево проблем будет выглядеть примерно так, как показано на Рисунке 10. Дерево проблем. Цветом выделены причины («корни») – серым, основная проблема («ствол») – желтым, следствия («крона») – зеленым.
Рисунок 10. Дерево проблем
«Дети не могут играть во дворе дома».
Дерево должно содержать как минимум 4-5 уровней. Если же получился «саженец» (ни корней, ни побегов), «куст» (большая крона, маленькие корни) или «мертвое дерево» (крона отсутствует), то анализ надо продолжить – «откапывать корни» и «растить ветви».
После построения дерева надо внимательно проверить, прослеживается ли логика построения по любой из цепочек от корня к вершине кроны. Если это не так, то «нелогичную» цепочку надо пересмотреть, возможно, переформулировать проблемы, а если это не удается – разорвать ее в месте, где логика нарушается, либо, наоборот, добавить недостающие элементы в логическую цепочку. Возможно, у вас появится несколько деревьев, не связанных между собой. Тем лучше, круг нашей работы сужается, не влияющие на основную проблему факты отошли в сторону сами собой.
Если неясно, какая из сформулированных проблем является следствием, а какая – причиной, надо постараться достичь согласия в группе по этому вопросу. Следует либо переформулировать проблемы в более общие, либо, наоборот, детализировать их так, чтобы все участники были согласны с прорисованной связью и понимали, почему она выглядит именно так. Часто приходится заменять одну проблему несколькими или добавлять новые формулировки проблем, которые были изначально упущены.
Процесс построения дерева можно считать завершенным тогда, когда ВСЕ участники обсуждения согласны с его структурой и причинно-следственными связями, прорисованными между элементами. Это требование является общим при завершении всех трех этапов аналитической фазы: все участники должны видеть одну и ту же картину, и толкование ее также должно быть единым.
Дерево проблем – ключевой элемент аналитической фазы. Оно является источником информации для проведения следующего этапа – анализа целей. На его выполнение чаще всего тратится до 50% всего времени на разработку проекта. Мы уверены, что вы уже понимаете, почему это так. Если дерево проблем построено качественно – дальнейшие шаги по разработке проектов будут проходить значительно быстрее, и для их выполнения надо будет лишь действовать по описанным ниже алгоритмам.
Итак, этап анализа проблем проводится группой, состоящей из ведущего и представителей заинтересованных сторон.
Сам процесс анализа состоит из:
• формулировки проблем на основе Схемы анализа заинтересованных сторон;
• определении, какие из них являются причинами, а какие – следствиями;
• построении «дерева проблем»;
• проверки логики его строения и окончательной корректировки.
При проведении анализа надо соблюдать требования, предъявляемые к формулировке проблем. Очень важна роль ведущего – фасилитатора, которая состоит в оживлении и направлении дискуссии в нужное русло, отслеживании и исправлении ошибок в формулировках проблем и логике построения дерева.
Читайте также
Строим бизнес как систему!
Строим бизнес как систему! Еще одна очень важная тема, которую нужно внимательно проработать на старте, – это то, чем и как вы будете управлять.Часто кажется, что предприниматель в бизнесе управляет людьми, продажами. На самом деле в правильно организованном бизнесе
СТРОИМ СХЕМУ АНАЛИЗА ЗАИНТЕРЕСОВАННЫХ СТОРОН
СТРОИМ СХЕМУ АНАЛИЗА ЗАИНТЕРЕСОВАННЫХ СТОРОН Что это такое? Это схема, на которой демонстрируются все заинтересованные в проекте стороны, а также существующие и желаемые связи между ними. Схема наглядно описывает сложившуюся на данный момент ситуацию.Для чего она нужна?
КАК ПОСТРОИТЬ «ДЕРЕВО ПРОБЛЕМ»?
КАК ПОСТРОИТЬ «ДЕРЕВО ПРОБЛЕМ»? Напомним, наша задача – сформулировать проблемы и установить причинноследственные связи между ними. Что такое причинно-следственные связи? Если одно событие является следствием другого (например, прошел дождь – асфальт мокрый), то между
СТРОИМ ПАРТНЕРСКИЕ ОТНОШЕНИЯ
Не то дерево
Не то дерево Мы знаем, что идеальных руководителей не существует и что любая управленческая функция требует особого поведения, особого стиля управления. Более того, нам известно, что ни одной организации не добиться успеха без команды руководителей, которые сообща
Дерево желания
Дерево желания Основные направления деятельности производственного подразделения Orange Kent H. Landsberg компании Sunclipse – управление, распространение, складирование и продажи. Когда подразделение впервые ввело систему подачи предложений, персонал проявлял к этому большой
Дерево Перехода
Дерево Перехода Когда решение о направлении действий принято, дерево перехода (ДП) помогает реализовать это решение (рис. 1.15). В нем определяется, что может препятствовать нашим действиям и как лучше преодолеть эти преграды. Оно также позволяет установить
3 Дерево текущей реальности
3 Дерево текущей реальности Если вы умудряетесь сохранять самообладание, когда все вокруг его теряют, значит, вы недооцениваете всей серьезности проблемы. Закон Эванса «Не так все просто!» – очень часто приходится слышать в ответ на предложение в кратчайшие сроки
5 Дерево будущей реальности
5 Дерево будущей реальности Заняться чем-то абсолютно новым – значит начать все с нуля, отказавшись от привычного и рискуя не овладеть непознанным. Айзек Азимов Представьте себе, что вы отвечаете за работу некой сложной системы, к примеру государственной системы
ДБР и дерево текущей реальности
ДБР и дерево текущей реальности Осуществляете ли вы стратегическое планирование или решаете одну конкретную проблему, начать необходимо с какой-то четко определенной отправной точки. Здесь пригодится ДТР: ключевая проблема и есть та отправная точка, от которой
Дерево будущей реальности и дерево перехода
Дерево будущей реальности и дерево перехода Как вы помните, нестандартная идея может выражаться как описанием неких желаемых условий, так и конкретным руководством к действию. ДБР по своей сути – это лаборатория, в которой мы испытываем эффективность своих идей. Это
6 Дерево перехода
6 Дерево перехода Нет ничего более сложного, опасного и безнадежного с точки зрения шансов на успех, чем внедрение нового порядка вещей. Николо Макиавелли Очень часто неординарные идеи на поверку оказываются лишь мечтами. Одно дело предложить, как решить проблему, и
Дерево перехода и дерево будущей реальности
Дерево перехода и дерево будущей реальности ДП помогает конкретизировать нестандартные идеи, которые сформулированы как описание общих условий при работе с деревом будущей реальности. В подобных случаях нестандартную идею из ДБР помещают в ДП в качестве задачи,
Дерево покупательских решений
Дерево покупательских решений Дерево покупательских решений – это модель принятия решения о покупке товара покупателем, которая выражается рейтинговым списком факторов выбора товара. В реальной жизни процесс выбора товара обычно «свернут» и для повседневных
Строим план тренинга
Строим план тренинга Стандарт – 21 день Чтобы тренинг хорошо продавался, он должен идти долго. Тренинг типа braindump продается очень плохо, так как не закрепляет результаты, даже если информация у вас отличная и заставляет на многие вещи взглянуть по-новому. Поэтому
Техника креативности «Дерево проблем»
Мы уже писали о том, что когда задача излагается образно, в виде метафоры, рисунка, иероглифа, сознание воспринимает её легче и легче справляется с решением.А самым понятным для сознания образом будет нечто архетипическое, глубинное, понятное всем культурам во все времена.
Один из таких вечных и древних архетипов – архетип Дерева.
Мировое Древо – это самый старый и универсальный символ, которым можно охватить, описать практически всё, что есть во Вселенной.
Поэтому неудивительно, что многие креативные техники работают с образом Древа, используя его по-всякому.
Итак, сейчас мы будем строить (и разрушать!) дерево Проблем.
Вот, алгоритм Ваших действий, при условии, что Вы «счастливый» обладатель проблемы, которую не знаете с какого боку начинать решать. Итак,
Подготовительный этап, этап слов
Шаг Первый.
Представьте свою Проблему в виде Задачи, которую просто нужно решить, в рабочем порядке. (так снимается «важность», другими словами, истерика).
Шаг Второй.
Продумайте и выпишите отдельным списком – список обстоятельств, мешающих выполнению задуманного. То, что нужно преодолеть.
Шаг третий.
Ранжируйте, классифицируйте эти препятствия в порядке убывания (или возрастания!) сложности… как хотите, главное, привнесите систему в Ваш «список жалоб».
Переходим непосредственно к рисунку Дерева
Шаг первый.
Шаг второй.
Свой тренинговый центр за 55 000 руб. Можно вести бизнес онлайн!
В стоимость входят комплект материалов для очного проведения всех программ + 2 дня живого обучения онлайн. Бессрочное право проведения 10 программ. Никаких дополнительных отчислений и платежей. Запуск за 2 дня.
Рисуем горизонтальные линии – это ветви нашего дерева. В каждой ветке пишем препятствия (по одному препятствию на одну ветку!). На нижних ветках – самые лёгкие препятствия, на высоких – самые сложные.
Представьте себе, что Вы – дровосек. Дровосеку всегда сложно обрубить ветви, которые расположены выше его роста, не правда ли?
Шаг третий.
Делаем из этого схематичного рисунка – рисунок красивый (дорисовываем детальки), чтобы все видели, что перед ними, действительно – дерево.
Здесь как нигде важно это правдоподобие, иначе пользы от такой древней и весьма архетипичной модели будет ноль. Ваше образное правополушарное мышление требует «красивых картинок», так дайте же их ему. Так Вам будет гораздо легче вжиться в роль дровосека с остро заточенным топором.
Это звучит неправдоподобно, но такая техника очень быстро приводит людей, ей овладевших, к решению проблемы.
И дело тут не в архетипе дерева, просто когда кто-либо начинает думать, особенно подключая образное мышление, его задачи решаются быстрее и легче, чем у других.
Сохраните статью, чтобы внимательно изучить материал
Что такое дерево решений и где его используют?
Ребята, привет! Сегодня команда ProductStar подготовила для вас статью, в которой мы рассмотрели общие принципы работы и области применения дерева решений. Материал подготовлен на основе работы Акобира Шахиди «Деревья решений: общие принципы»
Дерево решений — метод автоматического анализа больших массивов данных. В этой статье рассмотрим общие принципы работы и области применения.
Дерево решений — эффективный инструмент интеллектуального анализа данных и предсказательной аналитики. Он помогает в решении задач по классификации и регрессии.
В отличие от нейронных сетей, деревья как аналитические модели проще, потому что правила генерируются на естественном языке: например, «Если реклама привела 1000 клиентов, то она настроена хорошо».
Правила генерируются за счет обобщения множества отдельных наблюдений (обучающих примеров), описывающих предметную область. Поэтому их называют индуктивными правилами, а сам процесс обучения — индукцией деревьев решений.
В обучающем множестве для примеров должно быть задано целевое значение, так как деревья решений — модели, создаваемые на основе обучения с учителем. По типу переменной выделяют два типа деревьев:
дерево классификации — когда целевая переменная дискретная;
дерево регрессии — когда целевая переменная непрерывная.
Развитие инструмента началось в 1950-х годах. Тогда были предложены основные идеи в области исследований моделирования человеческого поведения с помощью компьютерных систем.
Дальнейшее развитие деревьев решений как самообучающихся моделей для анализа данных связано с Джоном Р. Куинленом (автором алгоритма ID3 и последующих модификаций С4.5 и С5.0) и Лео Брейманом, предложившим алгоритм CART и метод случайного леса.
Структура дерева решений
Рассмотрим понятие более подробно. Дерево решений — метод представления решающих правил в определенной иерархии, включающей в себя элементы двух типов — узлов (node) и листьев (leaf). Узлы включают в себя решающие правила и производят проверку примеров на соответствие выбранного атрибута обучающего множества.
Простой случай: примеры попадают в узел, проходят проверку и разбиваются на два подмножества:
первое — те, которые удовлетворяют установленное правило;
второе — те, которые не удовлетворяют установленное правило.
Далее к каждому подмножеству снова применяется правило, процедура повторяется. Это продолжается, пока не будет достигнуто условие остановки алгоритма. Последний узел, когда не осуществляется проверка и разбиение, становится листом.
Лист определяет решение для каждого попавшего в него примера. Для дерева классификации — это класс, ассоциируемый с узлом, а для дерева регрессии — соответствующий листу модальный интервал целевой переменной. В листе содержится не правило, а подмножество объектов, удовлетворяющих всем правилам ветви, которая заканчивается этим листом.
Пример попадает в лист, если соответствует всем правилам на пути к нему. К каждому листу есть только один путь. Таким образом, пример может попасть только в один лист, что обеспечивает единственность решения.
Терминология
Изучите основные понятия, которые используются в теории деревьев решений, чтобы в дальнейшем было проще усваивать новый материал.
Какие задачи решает дерево решений?
Его применяют для поддержки процессов принятия управленческих решений, используемых в статистистике, анализе данных и машинном обучении. Инструмент помогает решать следующие задачи:
Классификация. Отнесение объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные задачи.
Регрессия (численное предсказание). Предсказание числового значения независимой переменной для заданного входного вектора.
Описание объектов. Набор правил в дереве решений позволяет компактно описывать объекты. Поэтому вместо сложных структур, используемых для описания объектов, можно хранить деревья решений.
Процесс построения дерева решений
Основная задача при построении дерева решений — последовательно и рекурсивно разбить обучающее множество на подмножества с применением решающих правил в узлах. Но как долго надо разбивать? Этот процесс продолжают до того, пока все узлы в конце ветвей не станут листами.
Узел становится листом в двух случаях:
естественным образом — когда он содержит единственный объект или объект только одного класса;
после достижения заданного условия остановки алгоритм — например, минимально допустимое число примеров в узле или максимальная глубина дерева.
В основе построения лежат «жадные» алгоритмы, допускающие локально-оптимальные решения на каждом шаге (разбиения в узлах), которые приводят к оптимальному итоговому решению. То есть при выборе одного атрибута и произведении разбиения по нему на подмножества, алгоритм не может вернуться назад и выбрать другой атрибут, даже если это даст лучшее итоговое разбиение. Следовательно, на этапе построения дерева решений нельзя точно утверждать, что удастся добиться оптимального разбиения.
Популярные алгоритмы, используемых для обучения деревьев решений, строятся на базе принципа «разделяй и властвуй». Задают общее множество S, содержащее:
n примеров, для каждого из которых задана метка класса Ci(i = 1..k);
m атрибутов Aj(j = 1..m), которые определяют принадлежность объекта к тому или иному классу.
Тогда возможно три случая:
Примеры множества S имеют одинаковую метку Ci, следовательно, все обучающие примеры относятся к одному классу. В таком случае обучение не имеет смысла, потому что все примеры в модели будут одного класса, который и «научится» распознавать модель. Само дерево будет похоже на один большой лист, ассоциированный с классом Ci. Тогда его использование не будет иметь смысла, потому что все новые объекты будут относиться к одному классу.
Множество S — пустое множество без примеров. Для него сформируется лист, класс которого выберется из другого множества. Например, самый распространенный из родительского множества класс.
Множество S состоит из обучающих примеров всех классов Ck. В таком случае множество разбивается на подмножества в соответствии с классами. Для этого выбирают один из атрибутов Aj множества S, состоящий из двух и более уникальных значений: a1, a2, …, ap), где p — число уникальных значений признака. Множество S разбивают на p подмножеств (S1, S2, …, Sp), состоящих из примеров с соответствующим значением атрибута. Процесс разбиения продолжается, но уже со следующим атрибутом. Он будет повторяться, пока все примеры в результирующих подмножества не окажутся одного класса.
Третья применяется в большинстве алгоритмов, используемых для построения деревьев решений. Эта методика формирует дерево сверху вниз, то есть от корневого узла к листьям.
Сегодня существует много алгоритмов обучения: ID3, CART, C4.5, C5.0, NewId, ITrule, CHAID, CN2 и другие. Самыми популярными считаются:
ID3 (Iterative Dichotomizer 3). Алгоритм позволяет работать только с дискретной целевой переменной. Деревья решений, построенные на основе ID3, получаются квалифицирующими. Число потомков в узле неограниченно. Алгоритм не работает с пропущенными данными.
C4.5. «Продвинутая» версия ID3, дополненная возможностью работы с пропущенными значениями атрибутов. В 2008 году издание Spring Science провело исследование и выявило, что C4.5 — самый популярный алгоритм Data Mining.
CART (Classification and Regression Tree). Алгоритм решает задачи классификации и регрессии, так как позволяет использовать дискретную и непрерывную целевые переменные. CART строит деревья, в каждом узле которых только два потомка.
Основные этапы построения дерева решений
Построение осуществляется в 4 этапа:
Выбрать атрибут для осуществления разбиения в данном узле.
Определить критерий остановки обучения.
Выбрать метод отсечения ветвей.
Оценить точность построенного дерева.
Далее рассмотрим каждый подробнее.
Выбор атрибута разбиения
Разбиение должно осуществляться по определенному правилу, для которого и выбирают атрибут. Причем выбранный атрибут должен разбить множество наблюдений в узле так, чтобы результирующие подмножества содержали примеры с одинаковыми метками класса или были максимально приближены к этому. Иными словами — количество объектов из других классов в каждом из этих множеств должно быть как можно меньше.
Критериев существует много, но наибольшей популярностью пользуются теоретико-информационный и статистический.
Теоретико-информационный критерий
В основе критерия лежит информационная энтропия:
где n — число классов в исходном подмножестве, Ni — число примеров i-го класса, N — общее число примеров в подмножестве.
Энтропия рассматривается как мера неоднородности подмножества по представленным в нем классам. И даже если классы представлены в равных долях, а неопределенность классификации наибольшая, то энтропия тоже максимальная. Логарифм от единицы будет обращать энтропию в ноль, если все примеры узла относятся к одному классу.
Если выбранный атрибут разбиения Aj обеспечивает максимальное снижение энтропии результирующего подмножества относительно родительского, его можно считать наилучшим.
Но на деле об энтропии говорят редко. Специалисты уделяют внимание обратной величине — информации. В таком случае лучшим атрибутом будет тот, который обеспечит максимальный прирост информации результирующего узла относительно исходного:
где Info(S) — информация, связанная с подмножеством S до разбиения, Info(Sa) — информация, связанная с подмножеством, полученным при разбиении атрибута A.
Задача выбора атрибута в такой ситуации заключается в максимизации величины Gain(A), которую называют приростом информации. Поэтому теоретико-информационный подход также известен под название «критерий прироста информации.
Статистический подход
В основе этого метода лежит использования индекса Джини. Он показывает, как часто случайно выбранный пример обучающего множества будет распознан неправильно. Важное условие — целевые значения должны браться из определенного статистического распределения.
Если говорить проще, то индекс Джини показывает расстояние между распределениями целевых значений и предсказаниями модели. Минимальное значение показателя говорит о хорошей работе модели.
Индекс Джини рассчитывается по формуле:
где Q — результирующее множество, n — число классов в нем, pi — вероятность i-го класса (выраженная как относительная частота примеров соответствующего класса).
Значение показателя меняется от 0 до 1. Если индекс равен 0, значит, все примеры результирующего множества относятся к одному классу. Если равен 1, значит, классы представлены в равных пропорциях и равновероятны. Оптимальным считают то разбиение, для которого значение индекса Джини минимально.
Критерий остановки алгоритма
Алгоритм обучения может работать до получения «чистых» подмножеств с примерами одного класса. В таком случае высока вероятность получить дерево, в котором для каждого примера будет создан отдельный лист. Такое дерево не получится применять на практике из-за переобученности. Каждому примеру будет соответствовать свой уникальный путь в дереве. Получится набор правил, актуальный только для данного примера.
Переобучение в случае дерева решений имеет схожие с нейронными сетями последствия. Оно будет точно распознавать примеры из обучения, но не сможет работать с новыми данными. Еще один минус — структура переобученного дерева сложна и плохо поддается интерпретации.
Специалисты решили принудительно останавливать строительство дерева, чтобы оно не становилось «переобученным».
Для этого используют несколько подходов:
Ранняя остановка. Алгоритм останавливается после достижения заданного значения критерия (например, процентной доли правильно распознанных примеров). Преимущество метода — сокращение временных затрат на обучение. Главный недостаток — ранняя остановка негативно сказывается на точности дерева. Из-за этого многие специалисты советуют отдавать предпочтение отсечению ветей.
Ограничение глубины дерева. Алгоритм останавливается после достижения установленного числа разбиений в ветвях. Этот подход также негативно сказывается на точности дерева.
Задание минимально допустимого числа примеров в узле. Устанавливается ограничение на создание узлов с числом примером меньше заданного (например, 7). В таком случае не будут создаваться тривиальные разбиения и малозначимые правила.
Этими подходами пользуются редко, потому что они не гарантируют лучшего результата. Чаще всего, они работают только в каких-то определенных случаях. Рекомендаций по использованию какого-либо метода нет, поэтому аналитикам приходится набирать практический опыт путем проб и ошибок.
Отсечение ветвей
Без ограничения «роста» дерево решений станет слишком большим и сложным, что сделает невозможной дальнейшую интерпретацию. А если делать решающие правила для создания узлов, в которые будут попадать по 2-3 примера, они не лишатся практической ценности.
Поэтому многие специалисты отдают предпочтение альтернативному варианту — построить все возможные деревья, а потом выбрать те, которые при разумной глубине обеспечивают приемлемый уровень ошибки распознавания. Основная задача в такой ситуации — поиск наиболее выгодного баланса между сложностью и точностью дерева.
Но и тут есть проблема: такая задача относится к классу NP-полных задач, а они, как известно, эффективных решений не имеют. Поэтому прибегают к методу отсечения ветвей, который реализуется в 3 шага:
Строительство полного дерева, в котором листья содержат примеры одного класса.
Определение двух показателей: относительную точность модели (отношение числа правильно распознанных примеров к общему числу примеров) и абсолютную ошибку (число неправильно классифицированных примеров).
Удаление листов и узлов, потеря которых минимально скажется на точности модели и увеличении ошибки.
Отсечение ветвей проводят противоположно росту дерева, то есть снизу вверх, путем последовательного преобразования узлов в листья.
Главное отличие метода «отсечение ветвей» от преждевременной остановки — получается найти оптимальное соотношение между точностью и понятностью. При этом уходит больше времени на обучение, потому что в рамках этого подхода изначально строится полное дерево.
Извлечение правил
Иногда упрощения дерева недостаточно, чтобы оно легко воспринималось и интерпретировалось. Тогда специалисты извлекают из дерева решающие правила и составляют из них наборы, описывающие классы.
Для извлечения правил нужно отслеживать все пути от корневого узла к листьям дерева. Каждый путь дает правило с множеством условий, представляющих собой проверку в каждом узле пути.
Если представить сложное дерево решений в виде решающих правил (вместо иерархической структуры узлов), оно будет проще восприниматься и интерпретироваться.
Преимущества и недостатки дерева решений
Преимущества:
Формируют четкие и понятные правила классификации. Например, «если возраст