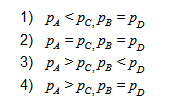что такое давление жидкости в физике

Давление жидкости

Формула давления жидкости отличается от формулы, с помощью которой можно рассчитать давление твердого тела. Потому, что давление жидкости не зависит от площади поверхности, на которую жидкость давит.

Закон Паскаля

Французский физик, Блез Паскаль, в 1653 году сформулировал закон: «Давление, которое мы оказываем на жидкость (или газ), она без изменения передаст в любую точку и во всех направлениях».

Мы немного упростим формулировку:

Жидкость (или газ) передает давление, оказанное на нее, одинаково и без изменений во все стороны.

Это значит, что на одной и той же глубине жидкость будет одинаково давить и на дно, и на стенки сосуда.

На рисунке 1 изображен сосуд, наполненный жидкостью. Высоту столбика жидкости – то есть, глубину, отсчитываем от поверхности жидкости.

Видно, что на разных глубинах давление отличается.

\[ \large \begin h_ <1>Формула давления жидкости

Формула, по которой можно посчитать давление жидкости:

​ \( P \left(\text<Па>\right) \) ​ – давление жидкости;

​ \( \displaystyle \rho_<\text<ж>> \left(\frac<\text<кг>><\text<м>^3> \right) \) ​ – плотность жидкости;

​ \( \displaystyle g \left(\frac<\text<м>>> \right) \) ​ – ускорение свободного падения;

Для большинства школьных задач можно принимать ​ \( \displaystyle g \approx 10 \left(\frac<\text<м>>> \right) \) ​;

​ \( h \left(\text<м>\right) \) ​ – высота столбика жидкости.

В формулу для давления жидкости не входит площадь S поверхности, на которую эта жидкость давит.

Поэтому, давление жидкости не зависит от площади. А давление твердого тела рассчитывают по другой формуле.

В некоторых задачах указывают объем используемой жидкости. И иногда просят рассчитать силу давления. Чтобы получить правильный ответ для таких задач, нужно уметь переводить площади и объемы в единицы системы СИ.

Сообщающиеся сосуды

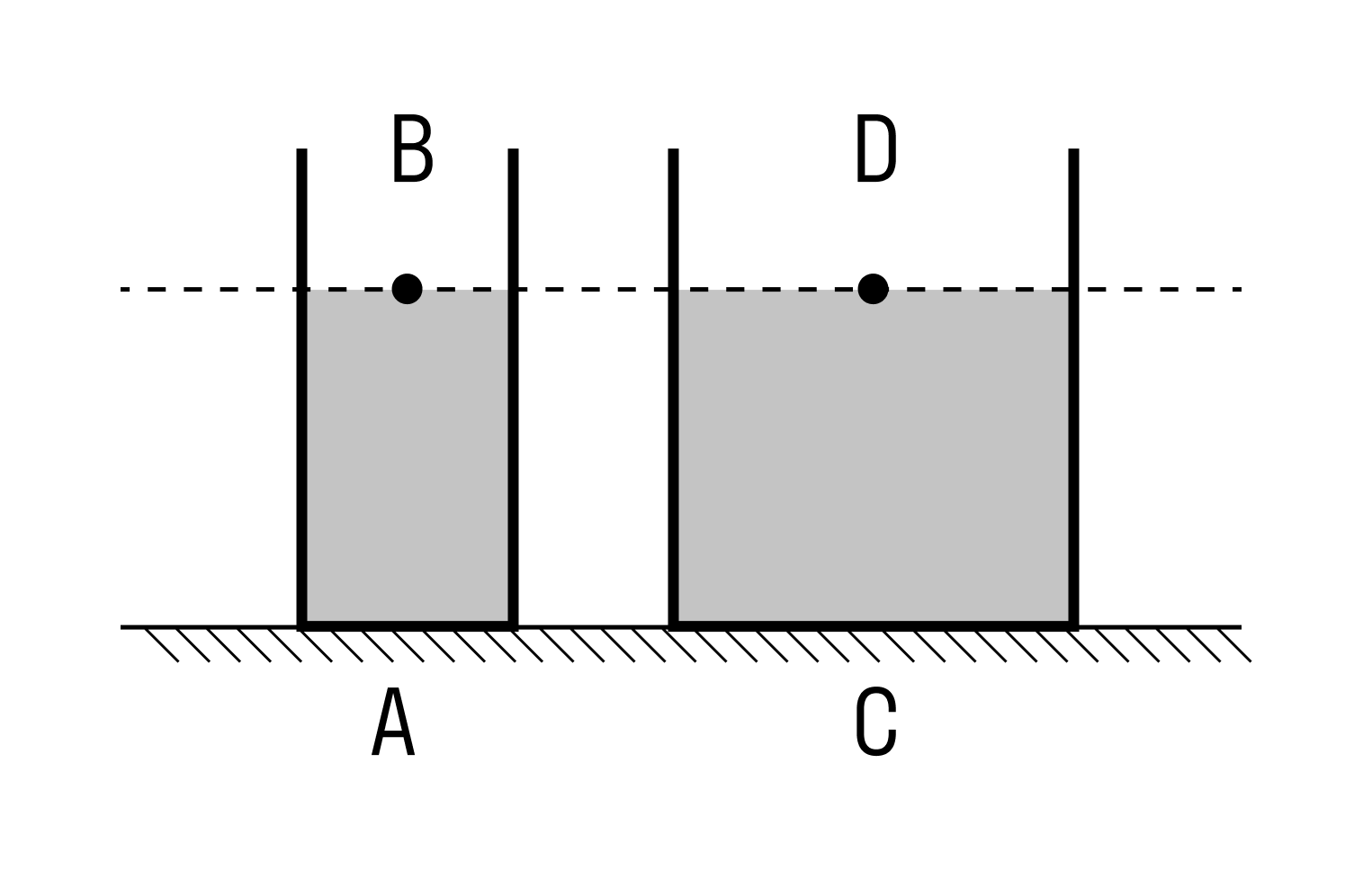
Сообщающиеся сосуды – это емкости, расположенные на плоской горизонтальной поверхности, у дна они соединяются трубками.

Если в один из сосудов начать наливать жидкость, то она будет распределяться по всем сосудам, так, что ее уровень будет одинаковым во всех сосудах (рис. 2).

Неважно, какую форму имеет сосуд. Давление жидкости во всех сосудах будет одинаковым. Поэтому одинаковой будет высота h столбика жидкости во всех сосудах.

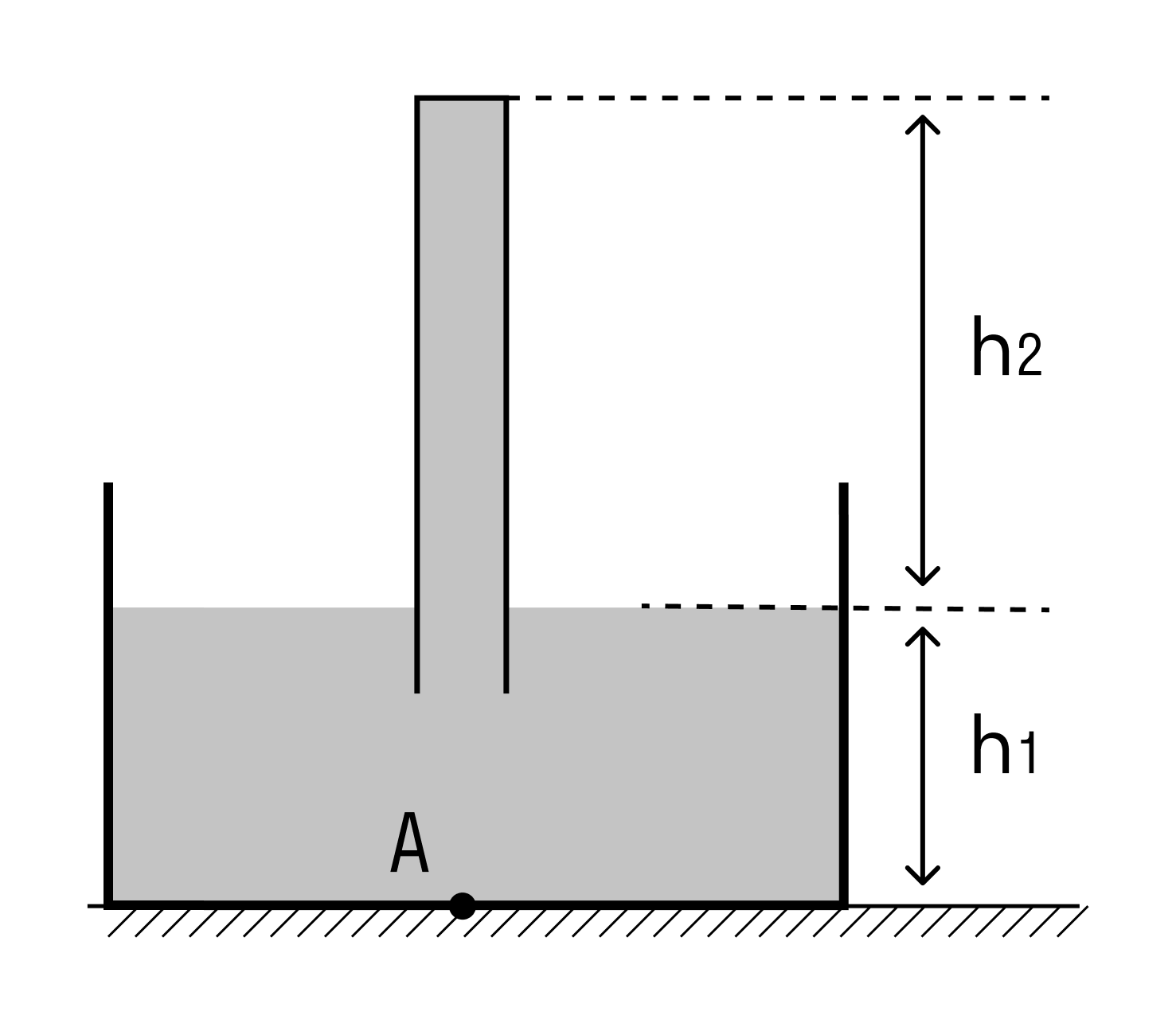
U-образное колено

U-образное колено – это два сообщающихся сосуда, диаметры сосудов одинаковые.

Жидкости, которые заливают в колено, не должны смешиваться (рис. 3). Например, можно залить в оду трубку воду, а в другую — масло.

Запишем формулы для расчета давления в левом \(P_<1>\) и правом \(P_<2>\) частях колена.

\[ \large \boxed <\beginP_ <1>= \rho_ <1>\cdot g \cdot h_ <1>\\ P_ <2>= \rho_ <2>\cdot g \cdot h_ <2>\end> \]

Чем больше разница плотностей двух жидкостей, тем больше отличаются высоты их столбиков.

При решении задач общую нижнюю часть колена не учитываем. На рисунке 3 она отделена от верхней части горизонтальной линией.

Давление столбиков, оставшихся в верхней части, будет одинаковым.

\( P_ <1>\) – давление жидкости в левой части колена;

\( P_ <2>\) – давление жидкости в правой части колена.

\[ \large \begin P_ <1>= P_ <2>\\ \rho_ <1>\cdot g \cdot h_ <1>= \rho_ <2>\cdot g \cdot h_ <2>\end \]

Обе части последнего уравнения разделим на ускорение свободно падения. Тогда получим соотношение для высот столбиков жидкости и их плотностей:

\[ \large \boxed < \rho_<1>\cdot h_ <1>= \rho_ <2>\cdot h_ <2>>\]

Высоты столбиков можно измерить линейкой. Зная плотность одной из жидкостей, можно найти плотность второй жидкости.

Примечание: Давление жидкостей часто измеряют в миллиметрах ртутного столба или метрах водяного столба. Переходите по ссылке, чтобы узнать, как связаны эти единицы измерения и как давление переводить в систему СИ.

Гидравлический пресс

Молекулы жидкости плотно упакованы, они прилегают друг к другу. Поэтому жидкости не сжимаемы! Это свойство жидкостей используют в гидравлическом прессе.

Гидравлический пресс – это два сообщающихся сосуда. Их называют цилиндрами. Диаметры цилиндров отличаются. Внутри каждого цилиндра вверх и вниз может свободно перемещаться поршень (рис. 4). Поршень плотно прилегает к стенкам цилиндра, чтобы жидкость из цилиндра не просачивалась наружу.

Перемещаясь, поршень из цилиндра вытесняет жидкость в соседний цилиндр. Объем жидкости, вытесненной из одного цилиндра, совпадает с объемом, перешедшим в другой цилиндр, так как жидкость не проливается наружу.

\[ \large \Delta V_ <1>= \Delta V_ <2>\]

\( \Delta V_ <1>\left(\text<м>^<3>\right) \) – объем жидкости, вытесненной из первого цилиндра;

\( \Delta V_ <2>\left(\text<м>^<3>\right) \) – объем жидкости, перешедшей во второй цилиндр.

Из геометрии известно, объем цилиндрической фигуры можно найти по формуле:

\( \Delta h \left(\text<м>\right) \) – высота столбика вытесненной жидкости;

\( S \left(\text<м>^<2>\right) \) – площадь поршня (или основания цилиндра);

Так как объемы вытесненной и перешедшей в другой цилиндр жидкостей равны, можем записать

\[ \large \Delta h_ <1>\cdot S_ <1>= \Delta h_ <2>\cdot S_ <2>\]

То есть, высоты столбиков отличаются во столько же раз, во сколько отличаются площади поршней.

Площадь поверхности поршня и его диаметр связаны соотношением:

\( S \left(\text<м>^<2>\right) \) – площадь поршня;

\( d \left(\text<м>\right) \) – диаметр поршня;

Давления в цилиндрах будут равны.

Поршни в цилиндрах не двигаются – т. е. находятся в равновесии. Запишем условия равновесия для поршней:

\[ \large \boxed< \frac>> + \rho_ <1>\cdot g \cdot h_ <1>= \frac>> + \rho_ <2>\cdot g \cdot h_ <2>> \]

Здесь дробью вида \(\displaystyle\large \frac\) обозначено давление твердого тела (ссылка) — поршня.

Назовем цилиндр большого диаметра большим цилиндром, а цилиндр малого диаметра – малым. Сформулируем принцип действия гидравлического пресса:

С помощью малой силы в малом цилиндре мы можем создавать большую силу в большом цилиндре.

Источник

Гидростатическое давление: формула и свойства.

Гидростатическое давление – это давление, производимое на жидкость силой тяжести.

Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматривается практическое приложение этих законов.

Для того, чтобы понять гидростатику необходимо определиться в некоторых понятиях и определениях.

В этой статье мы подготовили для Вас, всю необходимую информацию о гидростатическом давлении, начиная от закона Паскаля и определения формулы гидростатического давления и до свойств давления и применения законов гидростатики в повседневной жизни.

Содержание статьи

Закон Паскаля для гидростатики.

В 1653 году французским ученым Б. Паскалем был открыт закон, который принято называть основным законом гидростатики.

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Закон Паскаля легко понимается если взглянуть на молекулярное строение вещества. В жидкостях и газах молекулы обладают относительной свободой, они способны перемещаться друг относительно друга, в отличии от твердых тел. В твердых телах молекулы собраны в кристаллические решетки.

Относительная свобода, которой обладают молекулы жидкостей и газов, позволяет передавать давление производимое на жидкость или газ не только в направлении действия силы, но и во всех других направлениях.

Закон Паскаля для гидростатики нашел широкое распространение в промышленности. На этом законе основана работа гидроавтоматики, управляющей станками с ЧПУ, автомобилями и самолетами и многих других гидравлических машин.

Определение и формула гидростатического давления

Из описанного выше закона Паскаля вытекает, что:

Величина гидростатического давления не зависит от формы сосуда, в котором находится жидкость и определяется произведением

ρ – плотность жидкости

g – ускорение свободного падения

h – глубина, на которой определяется давление.

Для иллюстрации этой формулы посмотрим на 3 сосуда разной формы.

Во всех трёх случаях давление жидкости на дно сосуда одинаково.

Полное давление жидкости в сосуде равно

P0 – давление на поверхности жидкости. В большинстве случаев принимается равным атмосферному.

Сила гидростатического давления

Выделим в жидкости, находящейся в равновесии, некоторый объем, затем рассечем его произвольной плоскостью АВ на две части и мысленно отброс им одну из этих частей, например верхнюю. При этом мы должны приложить к плоскости АВ силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку a. Пусть на эту площадь воздействует сила ΔP.

Тогда гидростатическое давление формула которого выглядит как

представляет собой силу, действующую на единицу площади, будет называться средним гидростатическим давлением или средним напряжением гидростатического давления по площади ΔF.

Истинное давление в разных точках этой площади может быть разным: в одних точках оно может быть больше, в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление Рср будет тем меньше отличаться от истинного давления в точке а, чем меньше будет площадь ΔF, и в пределе среднее давление совпадет с истинным давлением в точке а.

Для жидкостей, находящихся в равновесии, гидростатическое давление жидкости аналогично напряжению сжатия в твердых телах.

Единицей измерения давления в системе СИ является ньютон на квадратный метр (Н/м 2 ) – её называют паскалем (Па). Поскольку величина паскаля очень мала, часто применяют укрупненные единицы:

килоньютон на квадратный метр – 1кН/м 2 = 1*10 3 Н/м 2

меганьютон на квадратный метр – 1МН/м 2 = 1*10 6 Н/м 2

Давление равное 1*10 5 Н/м 2 называется баром (бар).

Между всеми этими единицами существует следующее соотношение:

1ат = 1 кгс/см 2 = 0,98 бар = 0,98 * 10 5 Па = 0,98 * 10 6 дин = 10 4 кгс/м 2

Следует помнить что между технической атмосферой (ат) и атмосферой физической (Ат) существует разница. 1 Ат = 1,033 кгс/см 2 и представляет собой нормальное давление на уровне моря. Атмосферное давление зависит от высоты расположения места над уровнем моря.

Измерение гидростатического давления

На практике применяют различные способы учета величины гидростатического давления. Если при определении гидростатического давления принимается во внимание и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным. В этом случае величина давления обычно измеряется в технических атмосферах, называемых абсолютными (ата).

Часто при учете давления атмосферное давление на свободной поверхности не принимают во внимание, определяя так называемое избыточное гидростатическое давление, или манометрическое давление, т.е. давление сверх атмосферного.

Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным.

и измеряют также в технических атмосферах, называемых в этом случае избыточными.

Случается, что гидростатическое давление в жидкости оказывается меньше атмосферного. В этом случае говорят, что в жидкости имеется вакуум. Величина вакуума равняется разнице между атмосферным и и абсолютным давлением в жидкости

и измеряется в пределах от нуля до атмосферы.

Свойства гидростатического давления

Гидростатическое давление воды обладает двумя основными свойствами:
Оно направлено по внутренней нормали к площади, на которую действует;
Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).

Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.

Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на две составляющие – нормальную и касательную. Наличие касательной составляющей из-за отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению жидкости вдоль площадки, т.е. нарушило бы её равновесие.

Поэтому единственным возможным направлением гидростатического давления является его направление по нормали к площадке.

Если предположить что гидростатическое давление направлено не по внутренней, а по внешней нормали, т.е. не внутрь рассматриваемого объекта а наружу от него, то вследствие того, что жидкость не оказывает сопротивления растягивающим усилиям – частицы жидкости пришли бы в движение и её равновесие было бы нарушено.

Следовательно, гидростатическое давление воды всегда направлено по внутренней нормали и представляет собой сжимающее давление.

Из этого же правило следует, что если измениться давление в какой-то точке, то на такую же величину измениться давление в любой другой точке этой жидкости. В этом заключается закон Паскаля, который формулируется следующим образом: Давление производимое на жидкость, передается внутри жидкости во все стороны с одинаковой силой.

На применение этого закона основываются действие машин, работающих под гидростатическим давлением.

Ещё одним фактором влияющим на величину давления является вязкость жидкости, которой до недавнего времени приято было пренебрегать. С появлением агрегатов работающих на высоком давлении вязкость пришлось так же учитывать. Оказалось, что при изменении давления, вязкость некоторых жидкостей, таких как масла, может изменяться в несколько раз. А это уже определяет возможность использовать такие жидкости в качестве рабочей среды.

Источник

Закон Паскаля

Давление

Идущий по рыхлому снегу человек будет в него постоянно проваливаться. А вот на лыжах он сможет передвигаться по тому же самому снегу спокойно. Казалось бы, ничего не меняется — человек воздействует на снег с одинаковой силой и на лыжах, и без них.

Дело в том, что «проваливание» в снег характеризуется не только силой — оно также зависит от площади, на которую эта сила воздействует. Площадь поверхности лыжи в 20 раз больше площади поверхности подошвы, поэтому человек, стоя на лыжах, действует на каждый квадратный сантиметр с силой в 20 раз меньшей, чем без них.

Или, например, если вы будете с одинаковой силой втыкать кнопки в пробковую доску, легче войдет та кнопка, у которой более заостренный конец, так как его площадь меньше.

Резюмируем: результат действия силы зависит не только от ее модуля, направления и точки приложения, но и от площади поверхности, к которой эта сила приложена.

А теперь подтвердим этот вывод опытами, как настоящие физики.

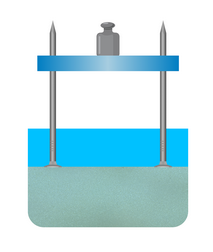
Возьмем небольшую доску и вобьем гвозди в ее углы. Также возьмем емкость с песком и поставим конструкцию из доски и гвоздей в эту емкость. Сначала расположим конструкцию шляпками вниз и поставим на нее гирю. Конструкция не утонет в песке, а только чуть-чуть углубится в него.

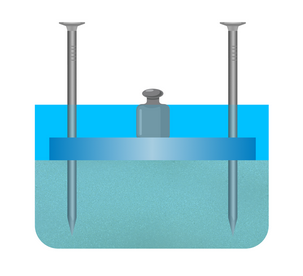
Затем перевернем конструкцию так, чтобы шляпки гвоздей оказались сверху и также поставим на доску гирю. Теперь конструкция утонет в песке.

От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия силы.

Во всех примерах мы говорили о действии силы, перпендикулярной поверхности. Чтобы охарактеризовать это действие, используется величина давление.

Давление

p = F/S

p — давление [Па]

F — сила [Н]

S — площадь [м 2 ]

Как уменьшить или увеличить давление

Тяжелый гусеничный трактор производит давление на почву, равное 40–50 кПа. Мальчик массой 45 кг производит давление всего лишь в 3 раза меньше, чем такой трактор. Это связано с большой площадью гусениц трактора.

В зависимости от того, какое давление хотят получить, площадь опор уменьшают или увеличивают. Например, чтобы уменьшить давление здания на грунт, в процессе строительства увеличивают площадь нижней части фундамента.

Шины грузовых автомобилей делают значительно шире легковых автомобилей. Чтобы убедиться в этом, обратите внимание на колеса какой-нибудь большой фуры. Самые широкие шины можно увидеть на автомобилях, предназначенных для передвижения в пустыне. Тот же лайфхак используется в шасси самолетов.

Обратную зависимость тоже применяют, например, при создании лезвий колющих и режущих инструментов. Острое лезвие имеет малую площадь, поэтому даже при небольшом нажатии создается большое давление.

Задачка раз

Книга лежит на столе. Масса книги равна 0,6 кг. Площадь ее соприкосновения со столом равна 0,08 м2. Определите давление книги на стол.

Решение

На стол будет давить сила, равная весу книги. Так как она покоится, ее вес будет равен силе тяжести. Следовательно:

p = mg/S = 0,6 × 10 / 0,08 = 75 Па

Ответ: давление книги на стол будет равно 75 Па.

Задачка два

Решение:

p = mg/S = 6 610 × 10 / 1,4 = 47 214 Па = 47,2 кПа

Ответ: давление трактора на почву составляет 47,2 кПа.

Задачка три

Человек массой 80 кг с сумкой весом 100 Н стоит неподвижно на полу. Сила давления подошв его ботинок на пол равномерно распределена по площади 600 см2. Какое давление человек оказывает на пол?

Решение

Масса человека: m = 80 кг.

Вес сумки, которую держит человек: P_c = 100 Н.

600 см 2 = 600 / 10 000 м 2 = 0,06 м 2

Давление — это отношение силы к площади, на которую она действует. В данном случае на площадь действует сила, равная сумме силы тяжести человека и веса сумки:

Поэтому давление, оказываемое человеком с сумкой на пол, равно:

p = (mg + P_с) / S = (80 × 10 + 100) / 0,06 = 15 000 Па = 15 кПа

Ответ: давление человека с сумкой на пол равно 15 кПа.

Определение закона Паскаля

Итак, мы подошли к формулировке закона Паскаля, и звучит она так:

Давление, производимое на жидкость или газ, передается в любую точку одинаково во всех направлениях.

Обратите внимание — закон работает только с жидкостями и газами. Дело в том, что молекулы жидких и газообразных веществ под давлением ведут себя совсем не так, как молекулы твердых тел. Если молекулы жидкости и газа движутся почти свободно, то молекулы твердых тел так не умеют. Они могут лишь колебаться, немного отклоняясь от исходного положения. Именно благодаря свободному передвижению молекулы газа и жидкости оказывают давление во всех направлениях.

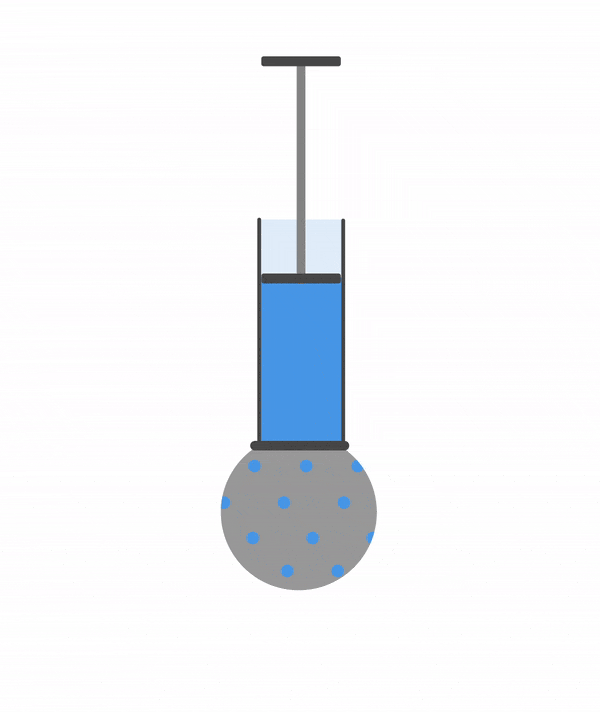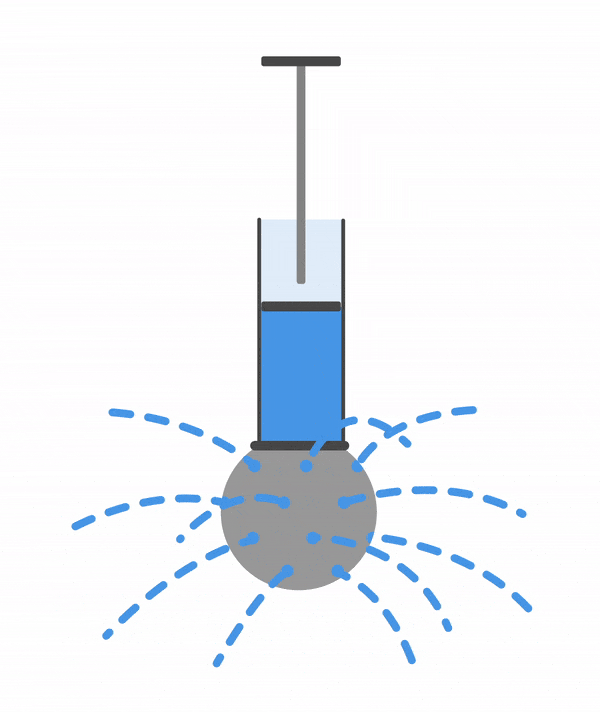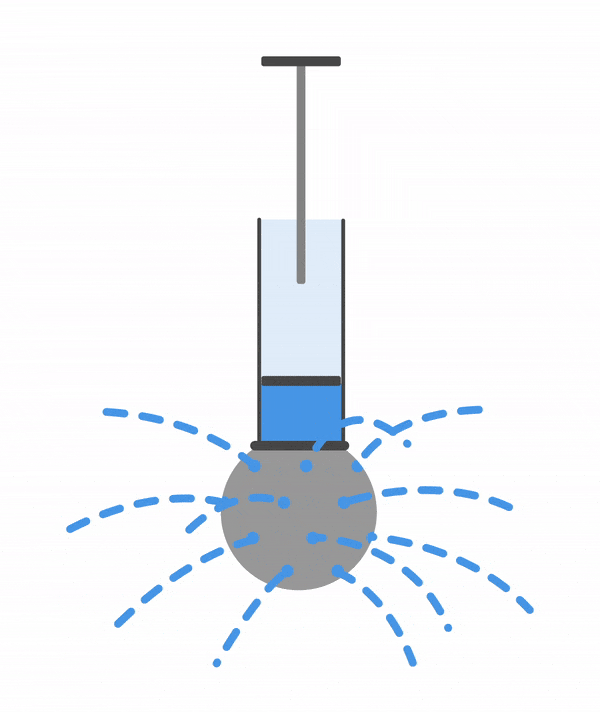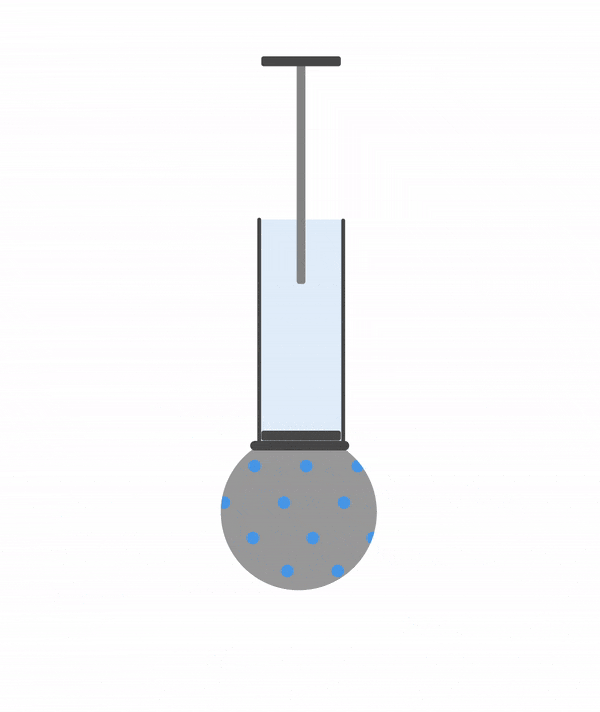
Рассмотрим опыт с шаром Паскаля, чтобы стало понятнее.

Присоединим к трубе с поршнем полый шар со множеством небольших отверстий. Зальем в шар воду и будем давить на поршень. Давление в трубе вырастет и вода будет выливаться через отверстия, причем напор всех струй будет одинаковым. Такой же результат получится, если вместо воды в шарике будет газ.

Давление жидкости

Из закона Паскаля следует, что раз давление передается одинаково во всех направлениях, то верхние слои жидкости давят на средние, средние — на нижние, нижние — на дно сосуда.

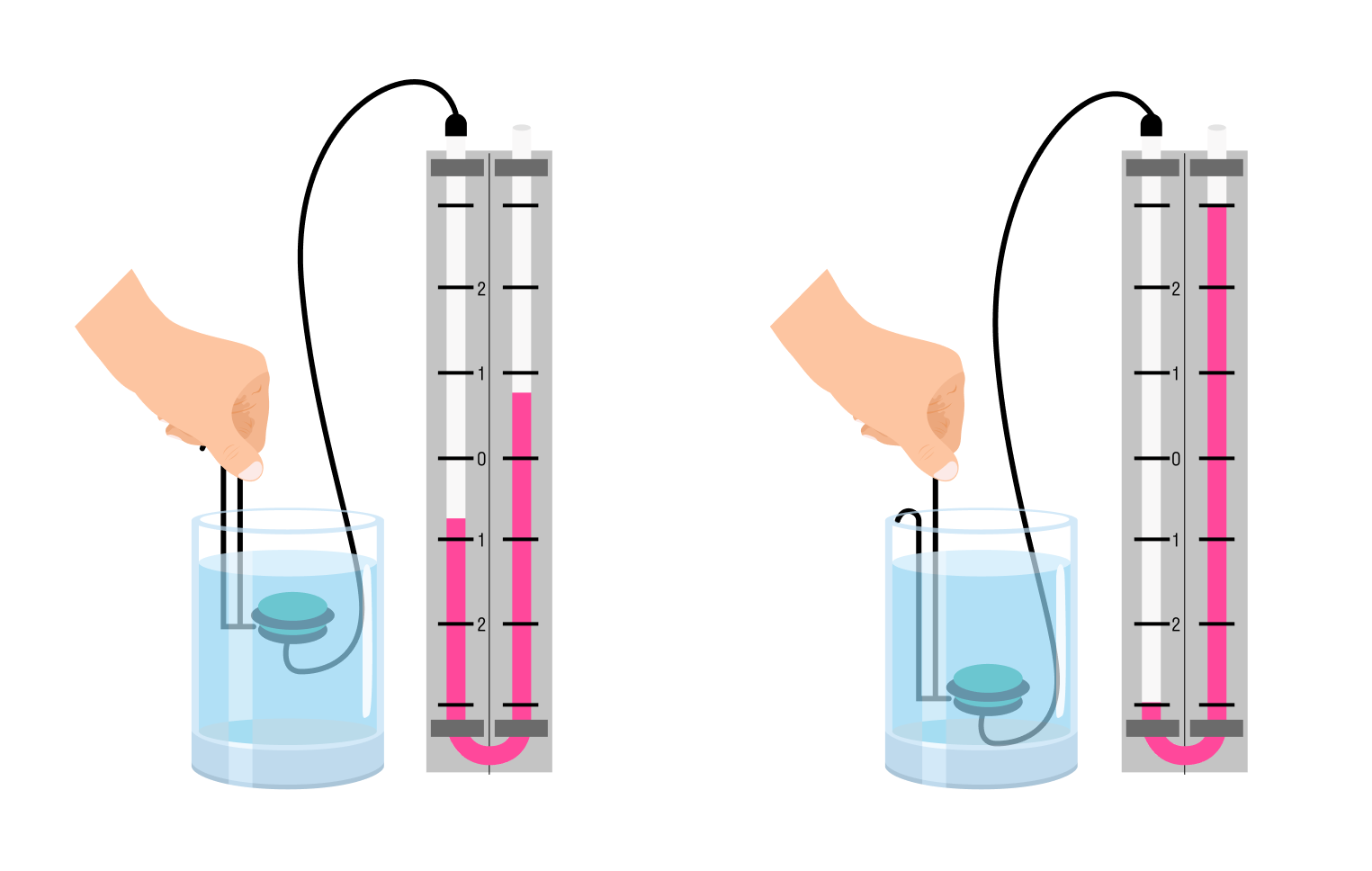
Давление внутри жидкости на одном и том же уровне одинаково по всем направлениям. С глубиной давление увеличивается.

Это утверждение проверяется с помощью манометра — прибора для измерения давления. Чем глубже мы измеряем давление, тем больше показания.

Давление столба жидкости

p = ρgh

ρ — плотность [кг/м 3 ]

h — высота столба жидкости [м]

g — ускорение свободного падения [м/с 2 ]

На Земле g = 9,8 м/с 2

Формула давления столба жидкости часто требуется в задачах.

Задачка раз

На горизонтальном столе стоят два цилиндрических сосуда — узкий и широкий (см. рисунок). В узкий сосуд налита вода, в широкий — керосин. Уровень жидкости в сосудах одинаковый. Сравните давления p жидкостей в точках A, B, C, D и выберите правильную пару утверждений.

Решение

Давление столба жидкости прямо пропорционально ее плотности и высоте столба. Плотность воды больше плотности керосина, следовательно, давление в точке A больше давления в точке C. Давления в точках B и D равны.

Правильный ответ указан под номером 4.

Задачка два

Решение

Поскольку вода не вытекает из пробирки, давление столба высотой h₂ на жидкость в сосуде высотой h₁ уравновешено давлением, которое оказывает вода в сосуде на столб воды в пробирке. Сосуд открытый, поэтому на него действует внешнее давление, которое и передается столбу воды. В результате столб воды в пробирке не оказывает дополнительного давления на точку А, поэтому давление, оказываемое водой на дно сосуда в точке А, равно p = ρgh1. Тогда:

p = ρgh₁ = 998 × 10 × 0,3 = 2 994 Па

Источник

Давление жидкости

Для понимания сути понятия «давление жидкости» нужно рассмотреть, что влияет на его формирование. Обычно рассматривают примеры по проще, а после переходят к изучению более сложных примеров. Гидростатическое давление в физике рассчитывается с учетом нескольких физических величин:

где \(p\) – давление слоя жидкости, Па;
\(ρ\) – плотность жидкости, кг/м 3 ;
\(g\) – ускорение свободного падения, м/с 2 ;
\(h\) – высота столба жидкости, м.

Значение давления столба жидкости

Для определения силы давления вводится понятие «площадь дна сосуда». При учете равного давления сила давления жидкости на дно сосуда рассчитается по формуле:

Эта формула показывает, что сила давления соизмерима с весом жидкости, при условии использования сосуда правильной цилиндрической формы. Также доказано, что эти вычисления также применимы для расчета давления жидкости в сосудах самой разнообразной формы. Здесь действует правило, гласящее, что давление жидкости на дно сосуда равно во всех точках, при условии одинаковой высоты столба жидкости и площади дня сосуда. Но при этом реальный вес жидкости сосуда неровной формы может отличаться от ее силы давления. Он может быть больше либо меньше, но конечное значение, рассчитанное по вышеуказанной формуле, будет справедливым.

Эксперименты Паскаля

Паскаль был одним из первых ученых, кто изобрел базовые формулы для расчета гидростатического давления. Свои эксперименты он проводил при помощи установки, позже названной его именем. Основным отличием этого прибора было применение специальных подставок, на которых он фиксировал различные сосуды с жидкостями и производил расчеты. Сосуды были самой различной формы, благодаря чему эта установка стала прорывом в сфере исследования физических свойств жидкостей. Также на этом приборе представлялось возможным фиксирование сосуда без дна. При этом вместо него могла крепиться пластина. Она была расположена на одном из плечей коромысла весов.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Устанавливая и перемещая груз на противоположном конце коромысла ученый наполнял сосуд жидкостью. Во время возникновения силы давления жидкости, большей, чем вес груза, жидкость выливалась наружу через пластину. Измеряя высоту столба жидкости, Паскаль мог вычислить величину силы давления жидкости на дно сосуда. Он сравнивал эти значения с весом груза.

Он старался достичь большой силы давления при ограниченном количестве воды. Он просто увеличивал глубину столба жидкости. Еще Паскаль проводил испытания такого рода: к бочке, наполненной до краев и плотно закрытой крышкой, он присоединял длинную трубку, через которую добавлял воду. При повышении давления до определенного значения бочка не выдерживала и начинала протекать. И получалось так, что данный эффект достигался при малом объеме добавленной воды. Это значит, что именно высота трубки, иными словами, высота столба жидкости создавала разрушительное давление на дно бочки. Таким образом, к разрушению емкости привело критическое значение давления.

Также при изучении поведения жидкости Паскаль заметил, что наклон стенок сосуда играет важную роль при распределении давления. Имеют место излишки давления, направленного в разные стороны. Если сосуд сужается кверху, то давление будет действовать вверх. Подобный эксперимент можно провести самому, для этого нужна установка, подобная прибору Паскаля. Нужен поршень, переходящий в трубку, на котором статически крепится цилиндр. Трубка ставится вертикально, затем в нее заливается вода, при этом необходимо следить, чтобы объем над поршнем заполнялся равномерно, потом цилиндр нужно поднять вверх.

Гидростатический парадокс

Гидростатический парадокс заключается в том, что давление жидкости не зависимо от ее объема и веса. Оно также не зависимо от формы сосуда, от размеров его дна, лишь только от высоты столба жидкости.

Не нашли что искали?

Просто напиши и мы поможем

Гидростатическое давление возможно определить для любой точки объема жидкости, а также для стенок сосуда.

Не нашли нужную информацию?

Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.

Гарантия низких цен

Все работы выполняются без посредников, поэтому цены вас приятно удивят.

Доработки и консультации включены в стоимость

В рамках задания они бесплатны и выполняются в оговоренные сроки.

Вернем деньги за невыполненное задание

Если эксперт не справился – гарантируем 100% возврат средств.

Тех.поддержка 7 дней в неделю

Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.

Тысячи проверенных экспертов

Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».

Гарантия возврата денег

Эксперт получил деньги, а работу не выполнил?
Только не у нас!

Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока

Гарантия возврата денег

В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы

Источник

• ← Хранилище почти заполнено что делать
• коррекционный детский сад что это значит →