что такое болометрическая светимость звезды
Звёздная величина (из Википедии)
Современное понятие видимой звёздной величины сделано таким, чтобы оно соответствовало величинам, приписанным звёздам древнегреческим астрономом Гиппархом во II веке до н. э. Гиппарх разделил все звёзды на шесть величин. Самые яркие он назвал звёздами первой величины, самые тусклые — звёздами шестой величины. Промежуточные величины он распределил равномерно между оставшимися звёздами.
Видимая звёздная величина зависит не только от того, сколько света излучает объект, но и от того, на каком расстоянии от наблюдателя он находится. Видимая звёздная величина считается единицей измерения блеска звезды, причём чем блеск больше, тем величина меньше, и наоборот.
В 1856 году Н. Погсон предложил формализацию шкалы звёздных величин. Видимая звёздная величина определяется по формуле:

Поскольку данная шкала относительная, то её нуль-пункт (0 m ) определяют как яркость такой звезды, у которой световой поток равен 10³ квантов /(см²·с·Å) в зелёном свете (шкала UBV) или 10 6 квантов /(см²·с·Å) во всём видимом диапазоне света. Звезда 0 m за пределами земной атмосферы создаёт освещённость в 2,54·10 −6 люкс.
Шкала звёздных величин является логарифмической, поскольку изменение яркости в одинаковое число раз воспринимается как одинаковое (закон Вебера — Фехнера). Кроме того, поскольку Гиппарх решил, что величина тем меньше, чем звезда ярче, то в формуле присутствует знак минус.
Следующие два свойства помогают пользоваться видимыми звёздными величинами на практике:
В наши дни видимая звёздная величина используется не только для звёзд, но и для других объектов, например, для Луны и Солнца и планет. Поскольку они могут быть ярче самой яркой звезды, то у них может быть отрицательная видимая звёздная величина.
Видимая звёздная величина зависит от спектральной чувствительности приёмника излучения (глаза, фотоэлектрического детектора, фотопластинки и т. п.)
Разности звёздных величин одного объекта в разных диапазонах U−B и B−V являются интегральными показателями цвета объекта, чем они больше, тем более красным является объект.
абсолютная
Абсолютная звёздная величина (M) определяется как видимая звёздная величина объекта, если бы он был расположен на расстоянии 10 парсек от наблюдателя. Абсолютная болометрическая звёздная величина Солнца +4,7. Если известна видимая звёздная величина и расстояние до объекта, можно вычислить абсолютную звёздную величину по формуле:
Соответственно, если известны видимая и абсолютная звёздные величины, можно вычислить расстояние по формуле
Абсолютная звёздная величина связана со светимостью следующим соотношением: 


Звёздные величины некоторых объектов
| Объект | m |
| Солнце | −26,7 |
| Луна в полнолуние | −12,7 |
| Вспышка Иридиума (максимум) | −9,5 |
| Сверхновая 1054 года (максимум) | −6,0 |
| Венера (максимум) | −4,4 |
| Земля (глядя с Солнца) | −3,84 |
| Марс (максимум) | −3,0 |
| Юпитер (максимум) | −2,8 |
| Международная космическая станция (максимум) | −2 |
| Меркурий (максимум) | −1,9 |
| Галактика Андромеды | +3,4 |
| Проксима Центавра | +11,1 |
| Самый яркий квазар | +12,6 |
| Самые слабые звёзды, наблюдаемые невооружённым глазом | От +6 до +7 |
| Самый слабый объект, заснятый в 8-метровый наземный телескоп | +27 |
| Самый слабый объект, заснятый в космический телескоп Хаббла | +30 |
| Объект | Созвездие | m |
| Сириус | Большой пёс | −1,47 |
| Канопус | Киль | −0,72 |
| α Центавра | Центавр | −0,27 |
| Арктур | Волопас | −0,04 |
| Вега | Лира | 0,03 |
| Капелла | Возничий | +0,08 |
| Ригель | Орион | +0,12 |
| Процион | Малый пёс | +0,38 |
| Ахернар | Эридан | +0,46 |
| Бетельгейзе | Орион | +0,50 |
| Альтаир | Орёл | +0,75 |
| Альдебаран | Телец | +0,85 |
| Антарес | Скорпион | +1,09 |
| Поллукс | Близнецы | +1,15 |
| Фомальгаут | Южная рыба | +1,16 |
| Денеб | Лебедь | +1,25 |
| Регул | Лев | +1,35 |
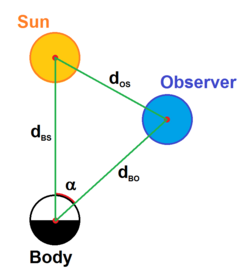
Солнце с разных расстояний
Что такое болометрическая светимость звезды
Основы астрофотометрии. Звездные величины
Основная задача астрофотометрии, как показывает само название этого раздела астрофизики, состоит в определении интенсивности излучений небесных тел.
Наблюдение звёзд
Блеск звезды связан с ее видимой звездной величиной основной формулой, которую мы сейчас выведем.
Изменение блеска между соседними градациями звездной величины определяется числом Погсона (равным 5 √100 = 2,5118864. ≈ 2,512)
Перемножая соотношения, находим, например,
Эти соотношения могут быть обобщены в следующем виде:
или, так как lg 2,512 = 0,4, то
В приведенных формулах величины m и n могут быть также и дробными (звездные величины не обязательно целые числа).
Измеряя при помощи фотометра отношение блеска звезд, можно определить по последней формуле разность звездных величин, но ничего нельзя сказать о нуль-пункте шкалы. Нуль-пункт выбирают условно, т. е. по некоторому соглашению, но в конце концов, поскольку блеск есть эквивалент освещенности, его можно связать с физическими величинами.
Полученные формулы позволяют распространить первоначальную шкалу (для шести звездных величин) как на более яркие небесные объекты, так и на слабые, невидимые для невооруженного глаза звезды.
Известно, что Венера светит как звезда минус 4-й величины, что блеск полной Луны эквивалентен блеску звезды минус 12-й величины, а Солнца – минус 27-й.
Если предел зрения невооруженного глаза около 6-й звездной величины, то в самый большой телескоп мира можно увидеть звезды 19-й величины, а сфотографировать более слабые – до 22-й.
Для иллюстрации подсчитаем, во сколько раз звезда первой величины светлее звезды 21-й звездной величины:
Звездная величина звезды зависит также и от свойств приемника излучения
Сначала оценки блеска звезд производились невооруженным глазом. Затем были сконструированы визуальные фотометры различных систем.
В поле зрения наиболее совершенного визуального фотометра наблюдатель видит две «соседние» звезды – наблюдаемую естественную и искусственную, и сравнивает их блеск. Искусственная звезда – это или отражение от блестящего шарика света неяркой лампочки или маленькое отверстие в диафрагме, освещенной стабильным источником света. Процесс наблюдения заключается в выравнивании блеска обеих звезд; в фотометре заключено устройство, позволяющее изменять свет искусственной звезды в известное число раз.
Сравнение блеска двух естественных звезд происходит в два приема – блеск каждой из них выравнивают с изменяемым блеском искусственной звезды. Так или иначе, но о блеске звезд судит глаз наблюдателя, и такие звездные величины называются визуальными. Очевидно, что они зависят от того, как чувствителен глаз к излучениям различных длин волн. Наиболее же чувствителен он к зеленым лучам.
Получая фотографические снимки звездного неба, мы находим пластинку покрытой множеством черных точек – изображений звезд. Степень почернения и диаметр изображения позволяют судить о так называемом фотографическом блеске звезды. Измеряя фотографический эффект, можно определить фотографическую звездную величину той или иной звезды.
Условно принято, что у белых звезд визуальная и фотографическая звездные величины одинаковы.
Разность между фотографической и визуальной звездными величинами называется показателем цвета.
У белых звезд, по условию, показатель цвета равен нулю. Так как фотографическая пластинка менее чувствительна к красным лучам, то у красных звезд показатель цвета положителен. Бывают иногда случаи, когда красная звезда, обладающая, например, пятой визуальной звездной величиной, фотографически будет восприниматься как слабая звезда восьмой величины. Таким образом, показатель цвета позволяет судить о цвете звезды.
Так как фотографический способ исследования звезд в значительной степени вытеснил визуальный, астрофизики разработали еще одну систему звездных величин, заменяющую визуальную. Используя ортохроматические пластинки и подбирая соответствующий светофильтр, а затем измеряя получившийся фотографический эффект, астрономы определяют так называемые фотовизуальные величины, которые призваны заменить визуальные.
К сожалению, точность определения звездных величин фотографическим способом невысока (0,1-0,2 звездной величины).
В фотоэлектрическом фотометре используется хорошо известный и изученный эффект, состоящий в том, что при освещении некоторых веществ в них возникает электрический ток, сила которого пропорциональна интенсивности падающего света. Таким образом, измерения «световых» величин заменяются измерениями тока, которые производятся гораздо точнее. Изобретение же очень чувствительных фотоумножителей позволяет измерять фототоки, возникающие при облучении фотокатодов слабым светом звезд.
В связи с этим были введены и получили широкое распространение более обоснованные фотометрические системы звездных величин, которые обозначаются латинскими буквами U, В и V.
Система U определяет звездные величины звезд в ультрафиолетовой области спектра, со средней длиной волны 3640 А.
Систему В можно считать отнесенной к длине волны 4445 А.
И, наконец, система V соответствует визуальной и относится к длине волны 5505 А.
Для создания таких систем перед фотоумножителем устанавливается специально подобранный светофильтр. Можно осуществить определения звездных величин в этой системе и фотографически. Таким образом, у каждой звезды теперь можно определить не один, а два показателя цвета U-В и В-V, т. е. сравнивать интенсивность излучения в разных участках спектра.
Разработан ряд и иных, еще более совершенных систем. За подробностями отсылаем к книге «Методы исследования переменных звезд», изданной под редакцией В. Б. Никонова («Наука», 1971).
Итак, мы видим, что современное понятие о звездной величине гораздо сложнее и зависит от многих факторов. Но если строго подойти к этому понятию, то только теперь оно получило должное научное обоснование. Дело в том, что самое простое понятие о визуальной звездной величине оказывается весьма неопределенным. Не существует «единого» человеческого глаза. У некоторых наблюдателей глаза оказываются более чувствительными, скажем, к красным лучам, у других – менее чувствительными, и у каждого визуально наблюдающего астронома своя собственная система визуальных звездных величин.
Существует все же одна система звездных величин, которая полностью свободна от произвола.
Это система болометрических звездных величин, в которой попросту суммируется все излучение звезды во всех участках спектра.
Определять такие величины можно было бы при помощи болометра, который измеряет полную энергию излучения звезды, если бы, конечно, не было поглощения света в земной атмосфере.
Болометрические величины непосредственно, как правило, не измеряют, а находят так называемые болометрические поправки. Придавая их, скажем, визуальным величинам, отыскивают болометрическую, т. е. энергетическую звездную величину, которая позволяет вычислять радиусы звезд.
При выполнении своих фотометрических наблюдений астроном-любитель сравнивает блеск изучаемого небесного светила с блеском соседних звезд сравнения. Для обработки такого наблюдения, т. е. для вычисления звездной величины из оценки блеска, нужно знать звездные величины звезд сравнения. Их можно найти в специальных звездных каталогах, которые основаны на более точных фотометрических определениях.
СОДЕРЖАНИЕ
Звезды и галактики
В звездной и галактической астрономии стандартное расстояние составляет 10 парсеков (около 32,616 световых лет, 308,57 петаметров или 308,57 триллионов километров). Звезда в 10 парсеков имеет параллакс 0,1 «(100 милли угловых секунд ). Галактики (и другие протяженные объекты ) намного больше 10 парсеков, их свет излучается над протяженным участком неба, и их общую яркость нельзя непосредственно наблюдать с относительно коротких расстояний, но используется то же соглашение. Величина галактики определяется путем измерения всего света, излучаемого над всем объектом, обработки этой интегральной яркости как яркости единственного точечного или звездообразного источника и вычисления величины этого точечного источника, как если бы наблюдается на стандартном расстоянии 10 парсеков. Следовательно, абсолютная величина любого объекта равна видимой величине, которую он имел бы, если бы находился на расстоянии 10 парсеков.
Видимая величина
Абсолютную звездную величину M также можно записать через видимую звездную величину m и звездный параллакс p :
или используя видимую звездную величину m и модуль расстояния μ :
Примеры
Ригель имеет визуальный величину м V 0,12 и расстояние около 860 световых лет:
Вега имеет параллакс p, равный 0,129 ″, и видимую звездную величину m V, равную 0,03:
M V знак равно 0,03 + 5 ( бревно 10 0,129 + 1 ) знак равно + 0,6. <\ displaystyle M _ <\ mathrm
Глаза Галактика имеет визуальный величину м V от 9,36 и модуля расстояния М от 31.06:
Болометрическая величина
Классически разница в болометрической величине связана с соотношением светимости в соответствии с:
что делает путем инверсии:
В августе 2015 года Международный астрономический союз принял Резолюцию B2, определяющую нулевые точки шкал абсолютной и кажущейся болометрической звездной величины в единицах СИ для мощности ( ватт ) и освещенности (Вт / м 2 ), соответственно. Хотя болометрические звездные величины использовались астрономами в течение многих десятилетий, наблюдались систематические различия в шкалах абсолютных звездных величин, представленные в различных астрономических справочниках, и отсутствовала международная стандартизация. Это привело к систематическим различиям в шкалах болометрических поправок. В сочетании с неверными предполагаемыми абсолютными болометрическими величинами Солнца это может привести к систематическим ошибкам в оценках светимости звезд (и других звездных свойств, таких как радиусы или возрасты, которые зависят от ее светимости).
В соответствии с Резолюцией B2 соотношение между абсолютной болометрической величиной звезды и ее светимостью больше не связано напрямую с (переменной) светимостью Солнца:
Новая шкала абсолютной звездной величины IAU навсегда отключает шкалу от переменной Солнца. Однако на этой шкале мощности SI номинальная светимость Солнца близко соответствует M bol = 4,74, значению, которое обычно принималось астрономами до резолюции IAU 2015 года.
Светимость звезды в ваттах может быть рассчитана как функция ее абсолютной болометрической величины M bol как:
используя переменные, как определено ранее.
Тела Солнечной системы ( H )
| ЧАС | Диаметр |
|---|---|
| 10 | 34 км |
| 12,6 | 10 км |
| 15 | 3.4 км |
| 17,6 | 1 км |
| 19,2 | 500 метров |
| 20 | 340 метров |
| 22,6 | 100 метров |
| 24,2 | 50 метров |
| 25 | 34 метр |
| 27,6 | 10 метров |
| 30 | 3,4 метра |
Видимая величина
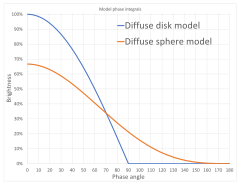
Планеты как диффузные сферы
Более продвинутые модели
Звёздные величины
«Звезда первой величины» — так часто говорят про человека всем известного, знаменитого, яркого. Но у астрономов звёзды первой величины — не самые яркие. На небе найдётся дюжина звёзд поярче. Какой же тогда они величины? Нулевой и минус первой.
Задача 2. Во сколько раз Сириус (−1,5 m ) ярче красной звезды Бетельгейзе (0,5 m ) из созвездия Ориона?
Задача 3 (самая трудная). А во сколько раз Бетельгейзе (0,5 m ) ярче, чем другая красная звезда — Антарес (1 m ) из созвездия Скорпиона?
Почему же глаз устроен так странно, что вдвое более яркие и вдвое более слабые объекты кажутся ему «одинаково удалёнными» по яркости? Ведь, например, каждому ясно, что 2 «ближе» к 1, чем к 4. А с яркостью не так: на рисунке яркость звёзд разных величин символически изображена отрезком соответствующей длины. А рядом — отрезки, соответствующие звёздным величинам, то есть тому, как мы воспринимаем эти яркости (точнее, разницу между ними). Это как если бы следующим делением линейки после 1 см у нас вместо 2 см стоял бы 1 м, и мы про все отрезки, что больше 10 см, говорили бы: «Это примерно метр!». А ещё следующим делением — после метра — было бы уже 100 м. Странная какая-то линейка.
Яркости звёзд (слева) и какими они нам кажутся (справа)
Такое восприятие немного похоже на то, как мы смотрим на уходящие вдаль рельсы. На ближайшей шпале мы можем разглядеть каждую трещину, каждую растущую возле неё травинку. Следующие несколько шпал нам тоже хорошо видны, но уже гораздо менее подробно, и разобраться, которая там из них восьмая, а которая — девятая, уже не так легко. А вдали шпалы и вовсе сливаются: не то чтобы нам их не видно, и, скажем, человека мы разглядим и с большого расстояния, но вот на какой он шпале стоит — на двухсотой или трёхсотой — нам уже непонятно, да и неважно, всё равно далеко. Так же устроена логарифмическая шкала: разница между 1 м и 1 м 20 см в ней гораздо больше, чем между 100 м и 101 м. Маленькую разницу между слабыми источниками света глаз замечает лучше, чем даже в 10 раз большую разницу между очень яркими.
Задача 6. На сколько децибел отличаются громкости звуков, энергии которых отличаются в тысячу раз? А в миллион раз?
Задача 7. Порог слышимости — самый тихий звук, который различает обычный человек, — это как раз 0 децибел. Считая, что без вреда для глаза можно смотреть на объекты в 5 раз ярче полной Луны, сравните диапазон яркостей, воспринимаемых человеческим глазом, с диапазоном громкостей, воспринимаемых ухом. Во сколько раз самый яркий подходящий нам свет ярче самого тусклого? А во сколько раз отличаются энергии самого громкого и самого тихого звуков? Какой инструмент универсальнее — глаз или ухо?
Можно ли, глядя на звезду, догадаться, яркая ли она на самом деле или просто близкая? Вообще-то нет. Но есть «подсказки». Это — цвет звезды: если она белая или голубая, значит — уж точно довольно яркая, хотя и не определить на глаз, просто яркая или чудовищно яркая. А если жёлтая — значит, на самом деле не очень-то яркая, скорее всего, похожа на наше Солнце. Вот с красными сложнее — они могут оказаться и совсем тусклыми, и ужасно яркими. Но про это — как-нибудь в другой раз. А пока — две довольно сложные задачки напоследок.
Задача 9. Звёзды А и В одинаковой светимости, но А в 2 раза дальше. Во сколько раз она слабее на небе? На сколько отличаются их звёздные величины? Во сколько раз дальше должна быть звезда, чтобы казаться на 10 m слабее другой такой же звезды?
Художник Алексей Вайнер
1. В 2,5 · 2,5 = 6,25 раз; в 2,5 · 2,5 · 2,5 ≈ 15,6 раз.
2. 0,5 m − (−1,5 m ) = 2 m ; разница опять в 2,5 · 2,5 = 6,25 раз.
4. Разница −12,7 m − (−26,7 m ) = 14 m ; 14 = 5 + 5+ 5 − 1. Значит, отличие в 100 · 100 · 100 : 2,5 = 400 000 раз.
6. 1000 = 10 · 10 · 10, поэтому громкость отличается на 3 · 10 = 30 дБ. Миллион — это 6 перемноженных десяток, каждое умножение на 10 соответствует изменению громкости на 10 дБ, поэтому разница 6 · 10 = 60 дБ. Это разница между тихим шёпотом и звуком проезжающего мимо грузовика.
7. Свет: 5 m − (−12,7 m ) = 17,7 m от слабой звезды до Луны, перепад между самым ярким и самым слабым 5 · 100 · 100 · 100 · 100 : (2,5 · 2,5) ≈ 100 млн раз. Звук: 120 дБ = 12 · 10 дБ, перепад 10 12 = 1 миллион миллионов раз. Выходит, у уха диапазон больше, чем у глаза. (Мы считали, что глаз адаптирован к ночному пейзажу.)
Разница 10 m — это в 100 · 100 = 10 4 раз. Значит, звезда в \( \sqrt <10000>\) = 100 раз дальше.
1 Подсчитывать энергию и число фотонов — на самом деле совсем не одно и то же, так как фотоны «разных цветов» несут разную энергию. Но здесь мы эти подробности обсуждать не будем.
2 Про шкалу громкости звуков читайте в статье А. Щетникова «Что такое децибел» в «Квантике» № 3 за 2016 год.