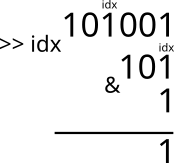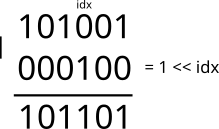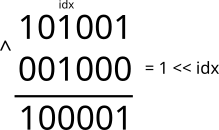что такое битовая маска
Работа с битовой маской
Доброго времени суток всем!
Часто возникает необходимость хранить данные логического типа для определенных таблиц. Например, таблица пользователей, такими данными могут быть поля активация пользователя, блокирование пользователя и др. Для таких полей удобно использовать битовую маску, при которой все данные хранятся в одном поле таблицы. Последнее время работаю с фреймверком Yii. Мне он нравится и во всем устраивает. Так вот, в процессе работы над несколькими проектами у меня появилось ряд наработок для работы с битовой маской под этот фреймверк.
Ими и хочу поделиться.
И так, создаем модель, наследуя от ActiveRecord:
Объявляем флаги. Для базового класса задаем флаг блокировки, который может быть использован для большинства моделей.
Значение константы соответствует номеру бита. Если биты будут одинаковые, флаги будут перетираться.
Дальше пишем методы для работы с флагами:
Модели, которые должны работать с флагами делаем наследниками этого класса и добавляем в таблицу поле flags.
Теперь, например, чтобы проверить, заблокирована ли новость, можно выполнить:
или чтобы заблокировать новость:
или, например, чтобы отфильтровать незаблокированные новости:
В модель можно добавить столько флагов, сколько позволяет разрядность типа поля в базе данных.
Если материал оказался полезным, я буду рад опубликовать продолжение данной темы, рассказав о готовых средствах администрирования флагов через CgridView и экшн с базовыми средствами настройки.
O.3 – Битовые манипуляции с побитовыми операторами и битовыми масками
В предыдущем уроке о побитовых операторах (O.2 – Побитовые операторы) мы обсудили, как различные побитовые операторы применяют логические операции к каждому биту в операндах. Теперь, когда мы понимаем, как они работают, давайте посмотрим, как они чаще всего используются.
Битовые маски
Чтобы управлять отдельными битами (например, устанавливать их в 1 или сбрасывать в 0), нам нужен способ идентифицировать конкретные биты, которыми мы хотим манипулировать. К сожалению, побитовые операторы не умеют работать с битовыми позициями. Вместо этого они работают с битовыми масками.
Битовая маска – это предопределенный набор битов, который используется для выбора того, какие конкретные биты будут изменены при последующих операциях.
Рассмотрим случай из реальной жизни, когда вы хотите покрасить оконную раму. Если не проявить осторожность, вы рискуете покрасить не только оконную раму, но и само стекло. Вы можете купить малярный скотч и приклеить его к стеклу и другим частям, которые не нужно красить. Затем, когда вы будете красить, малярный скотч будет блокировать попадание краски на всё, что вы не хотите красить. В конце концов, окрашиваются только немаскированные части (те части, которые вы хотите покрасить).
Битовая маска, по сути, выполняет ту же функцию для битов – битовая маска блокирует побитовые операторы от прикосновения к битам, которые мы не хотим изменять, и позволяет получить доступ к тем, которые мы действительно хотим изменить.
Давайте сначала узнаем, как определять простые битовые маски, а затем мы покажем, как их использовать.
Определение битовых масок в C++14
Самый простой набор битовых масок – это определение одной битовой маски для каждой битовой позиции. Мы используем нули, чтобы замаскировать биты, которые нам не нужны, и единицы, чтобы обозначить биты, которые мы хотим изменить.
Хотя битовые маски могут быть литералами, их часто определяют как символьные константы, поэтому им можно дать осмысленное имя и легко использовать повторно.
Поскольку C++14 поддерживает двоичные литералы, определить эти битовые маски очень просто:
Теперь у нас есть набор символьных констант, представляющих каждую битовую позицию. Мы можем использовать их для манипулирования битами (вскоре мы покажем, как это сделать).
Определение битовых масок в C++11 или в более ранних версиях
Поскольку C++11 не поддерживает двоичные литералы, то для установки символьных констант мы должны использовать другие методы. Для этого есть два хороших способа. Менее понятным, но более распространенным является использование шестнадцатеричных чисел. Если вам нужно напомнить о шестнадцатеричной системе счисления, еще раз посмотрите урок «4.13 – Литералы».
Это может быть трудно читать. Один из способов упростить задачу – использовать оператор сдвига влево, чтобы сместить бит в нужное место:
Проверка бита (чтобы узнать, установлен ли он в 1, или нет)
Теперь, когда у нас есть набор битовых масок, мы можем использовать их вместе с переменной битовых флагов для управления этими битовыми флагами.
Чтобы определить, установлен ли бит в 1 (включен, on) или сброшен в 0 (выключен, off), мы используем побитовое И в сочетании с битовой маской для соответствующего бита:
Эта программа напечатает:
Установка бита в 1
Чтобы установить бит в 1, мы используем присваивание с побитовым ИЛИ (оператор |= ) в сочетании с битовой маской для соответствующего бита:
Эта программа напечатает:
Мы также можем установить в 1 несколько бит одновременно, используя побитовое ИЛИ:
Сброс бита в 0
Чтобы сбросить бит в 0, мы используем побитовое И и побитовое НЕ вместе:
Эта программа напечатает:
Мы можем сбросить в 0 несколько бит одновременно:
Инвертирование бита
Чтобы инвертировать (переключить на противоположное) состояние бита, мы используем побитовое исключающее ИЛИ:
Эта программа напечатает:
Мы можем инвертировать несколько бит одновременно:
Битовые маски и std::bitset
Зачем это нужно? Функции позволяют изменять только отдельные биты. Побитовые операторы позволяют изменять сразу несколько битов.
Эта программа напечатает:
Делаем битовые маски более осмысленными
Присвоение нашим битовым маскам имен » mask1 » или » mask2 » говорит нам, какой бит обрабатывается, но не дает нам никакой индикации, для чего на самом деле используется этот битовый флаг.
Лучше всего давать вашим битовым маскам полезные имена, чтобы документировать значение ваших битовых флагов. Вот пример из игры, которую мы могли бы написать:
Вот тот же пример, реализованный с использованием std::bitset :
Когда битовые флаги наиболее полезны?
Проницательные читатели могут заметить, что приведенные выше примеры на самом деле не экономят память. 8 логических значений обычно занимают 8 байтов. Но в приведенных выше примерах используется 9 байтов (8 байтов для определения битовых масок и 1 байт для переменной флага)!
Битовые флаги имеют наибольший смысл, когда у вас много идентичных переменных-флагов. Например, в приведенном выше примере представьте, что вместо одного человека ( me ) у вас было бы 100. Если вы использовали 8 логических значений на человека (по одному для каждого возможного состояния), вы использовали бы 800 байт памяти. С битовыми флагами вы должны использовать 8 байт для битовых масок и 100 байт для переменных битовых флагов, в общей сложности 108 байт памяти – примерно в 8 раз меньше памяти.
Для большинства программ объем памяти, сэкономленный с помощью битовых флагов, не стоит дополнительного усложнения. Но в программах, где есть десятки тысяч или даже миллионы похожих объектов, использование битовых флагов может существенно сократить использование памяти. Это полезный способ оптимизации, если она вам понадобится.
Есть еще один случай, когда использование битовых флагов и битовых масок может иметь смысл. Представьте, что у вас есть функция, которая может принимать любую комбинацию из 32 различных параметров. Один из способов написать эту функцию – использовать 32 отдельных логических параметра:
Надеюсь, вы дадите своим параметрам более информативные имена, но суть здесь в том, чтобы показать вам, насколько плох длинный список параметров.
Если вместо этого вы определили функцию, используя битовые флаги, например:
Вы сможете использовать битовые флаги для передачи только тех параметров, которые вам нужны:
Это не только намного удобнее для чтения, но и, вероятно, будет более производительным, поскольку включает всего 2 операции (одно побитовое ИЛИ и одно копирование параметра).
Это одна из причин, по которой OpenGL, хорошо зарекомендовавшая себя библиотека трехмерной графики, решила использовать параметры битовых флагов вместо последовательностей множества логических параметров.
Вот пример вызова функции из OpenGL:
GL_COLOR_BUFFER_BIT и GL_DEPTH_BUFFER_BIT – это битовые маски, определенные следующим образом (в gl2.h ):
Битовые маски, включающие несколько битов
Хотя битовые маски часто используются для выбора одного бита, их также можно использовать для выбора нескольких битов. Давайте посмотрим на немного более сложный пример, в котором мы это делаем.
Цветные дисплеи, такие как телевизоры и мониторы, состоят из миллионов пикселей, каждый из которых может отображать точку цвета. Точка цвета состоит из трех световых лучей: красного, зеленого и синего (RGB – red, green, blue). Изменяя интенсивность этих цветов, можно получить любой цвет в цветовом спектре. Обычно яркость R, G и B для пикселя представлена 8-битовым целочисленным типом без знака. Например, красный пиксель будет иметь R = 255, G = 0, B = 0. У фиолетового пикселя R = 255, G = 0, B = 255. Средне-серый пиксель будет иметь R = 127, G = 127, B = 127.
При присвоении значений цвета пикселю, помимо R, G и B, часто используется 4-е значение, называемое A. «A» означает «альфа», и оно определяет, насколько прозрачным будет цвет. Если A = 0, цвет полностью прозрачный. Если A = 255, цвет непрозрачный.
R, G, B и A обычно хранятся как одно 32-битное целое число, в котором для каждого компонента используется 8 бит:
| биты 31-24 | биты 23-16 | биты 15-8 | биты 7-0 |
|---|---|---|---|
| RRRRRRRR | GGGGGGGG | BBBBBBBB | AAAAAAAA |
| красный | зеленый | синий | альфа |
Следующая программа просит пользователя ввести 32-битное шестнадцатеричное значение, а затем извлекает из него 8-битные цветовые значения для R, G, B и A.
Эта программа дает следующий результат:
В приведенной выше программе мы используем побитовое И для запроса интересующего нас набора из 8 бит, а затем сдвигаем их вправо в 8-битное значение, чтобы мы могли распечатать его как шестнадцатеричное значение.
Резюме
Обобщим, как устанавливать, сбрасывать, инвертировать и запрашивать битовые флаги:
Чтобы запросить состояния битов, мы используем побитовое И:
Для установки битов в 1 (включения) используем побитовое ИЛИ:
Чтобы сбросить биты в 0 (очистить, выключить), мы используем побитовое И с побитовым НЕ:
Чтобы инвертировать состояния битов, мы используем побитовое исключающее ИЛИ:
Небольшой тест
Вопрос 1
Для заданной программы:
a) Напишите строку кода, чтобы сделать статью просматриваемой (включить флаг option_viewed ).
b) Напишите строку кода, чтобы проверить, была ли удалена статья (флаг option_deleted ).
c) Напишите строку кода, чтобы сбросить у статьи статус избранная (сбросить флаг option_favorited ).
Ожидаемый результат (при условии, что вы выполнили задание (а):
Вопрос 2
Дополнительное задание: почему следующие две строки идентичны?
Закон Де Моргана гласит, что если мы распространяем НЕ, нам нужно поменять ИЛИ на И, и наоборот. Поэтому,
Битовые маски. Динамическое программирование по маскам
Битовые маски
Чаще всего массивы bool небольшого размера испольуются для обозначения некоторого подмножества объектов, выбранного из множества. Например, для обозначения элементов с индексами \(1\) и \(4\) (0-индексация), выбранных из множества из пяти элементов используется массив \(\
Операции с битовыми масками
Для работы с масками используются побитовые операции \(and, or, xor\), и битовые сдвиги.
int c = a & b; // маска c равна пересечению масок a и b
int c = a | b; // маска c равна объединению масок a и b
Для получения значения индивидуального бита используется комбинация битового сдвига вправо и операции \(and\). Сначала нам нужно сдвинуть биты маски так, чтобы нужный бит оказался самым младшим (находился справа). Затем нам нужно откинуть все остальные биты маски. Реализуется это следующим образом:
int bit = (a >> idx) & 1; // bit равен значению idx-го бита в маске a
Для установки значения определённого бита маски в true мы должны применить к нему операцию \(or\ true\). Реализуется это так (ко всем остальным битам применяется \(or\ false\), не имеющая никакого эффекта):
Для изменения значения определённого бита на противоположное, нужно применить к нему операцию \(xor\ true\). Ко всем остальным битам применяется \(xor\ false\), также не имеющая никакого эффекта:
Это самые распространённые операции, выполняемые с масками. Существует множество других, здесь не приведённых, но все они основаны на \(and, or, xor\), и сдвигах.
Динамическое программирование по подмножествам
Битовые маски часто используются как параметры для динамического программирования. Такой вид ДП называется ДП по маскам, или ДП по подмножествам.
Существует \(N\) городов, между некоторыми из которых есть дороги. Требуется обойти все города, вернувшись в первый, так, чтобы длина пути была минимальной.
Для простоты реализации примем, что города являются точками на геометрической плоскости, и между каждой парой есть путь, длина которого равна расстоянию между точками.
Запись \(\<0\>\) обозначает маску, обозначающую множество, состоящее только из элемента \(0\).
Формула перехода для ДП выглядит так:
Запись \(mask \backslash i\) обозначает множество \(mask\) без элемента \(i\).
Формула перехода обозначает следующее: чтобы попасть в вершину \(i\), нужно перейти в неё из какой-либо другой вершины \(j\), также входящей в \(mask\). Из всех таких вершин нужно выбрать такую, что общая длина пути в \(i\) будет наименьшей. Общая длина пути рассчитывается как длина пути в \(j\) (\(dp[mask \backslash i][j]\)) плюс длина пути из \(j\) в \(i\) (\(dst(j, i)\)).
Запись \(\mathbb
Может показаться, что порядок пересчёта такого ДП будет достаточно сложным. На самом деле это не так: заметьте что для пересчета \(dp[mask][i]\) нам нужно, чтобы уже был посчитан ответ для маски \(mask \backslash i\). Можно легко доказать, что в численном выражении \(mask \backslash i\) будет гарантированно меньше \(mask\), так как на некоторой позиции в \(mask\) будет находиться бит \(1\), а в \(mask \backslash i\) бит \(0\). Значит, можно просто пересчитывать ДП в порядке возрастания значения \(mask\) в численном выражении.
Битовая маска
Битовая маска — определённые данные, которые используются для маскирования — выбора отдельных битов или полей из нескольких битов из двоичной строки или числа.
Применение
Например, для получения значения пятого бита (считая слева) числа 10111011 нужно использовать маску 00001000 и применить операцию побитового логического «И» (конъюнкцию). В результате получится:
Подобное число на языках, использующих вместо логического типа числовые типы, например в Си, будет означать истину или ложь, если этот бит принимает соответствующее значение. На языках, например, C++, имеющие логические типы, необходимо произвести приведение типа.
Использование
Основные плюсы и недостатки:
Сфера использования в основном в интерфейсах, где приоритет отдаётся экономии памяти:
См. также
Полезное
Смотреть что такое «Битовая маска» в других словарях:
Маска (значения) — Маска: В Викисловаре есть статья «маска» Маска предмет, накладка на лицо, который надевается, чтобы не быть узнанным либо для защиты лица … Википедия
Битовая карта — (англ. bitmap, bitset, bit array) набор последовательно записанных двоичных разрядов, то есть последовательность (массив) битов. Содержание 1 Применение 1.1 В цифровых изображениях … Википедия
Маска подсети — В терминологии сетей TCP/IP маской подсети или маской сети называется битовая маска, определяющая, какая часть IP адреса узла сети относится к адресу сети, а какая к адресу самого узла в этой сети. Например, узел с IP адресом 12.34.56.78 и… … Википедия
Маска сети — В терминологии сетей TCP/IP маской подсети или маской сети называется битовая маска, определяющая, какая часть IP адреса узла сети относится к адресу сети, а какая к адресу самого узла в этой сети. Например, узел с IP адресом 12.34.56.78 и маской … Википедия
адресная маска — Битовая маска, используемая для выбора битов из адреса IP для адресации подсети. Маска имеет размер 32 бита и выделяет адреса IP сети и один или несколько битов адреса хоста. Иногда называется маской подсети. … … Справочник технического переводчика
Битовый вектор — Битовая карта (англ. bitmap, bitset, bit array) набор последовательно записанных двоичных разрядов, то есть последовательность (массив) битов. Содержание 1 Применение 1.1 В цифровых изображениях 1.2 … Википедия
Битовый массив — Битовая карта (англ. bitmap, bitset, bit array) набор последовательно записанных двоичных разрядов, то есть последовательность (массив) битов. Содержание 1 Применение 1.1 В цифровых изображениях 1.2 … Википедия
Вихрь Мерсенна — (англ. Mersenne twister, MT) генератор псевдослучайных чисел (ГПСЧ), разработанный в 1997 году японскими учёными Макото Мацумото (яп. 松本 眞) и Такудзи Нисимура (яп. 西村 拓士). Вихрь Мерсенна основывается на свойствах простых чисел Мерсенна… … Википедия
SSE4 — SSE4 новый набор команд микроархитектуры Intel Core, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD)[1]. Он был анонсирован 27 сентября 2006 года, однако детальное описание стало доступно только весной… … Википедия
SSE4.1 — SSE4 это новый набор команд Intel Core микроархитектуры, впервые реализованный в процессорах серии Penryn (не следует путать с SSE4A от AMD). Он был анонсирован 27 Сентября 2006, однако детальное описание стало доступно только весной 2007, свежее … Википедия
СОДЕРЖАНИЕ
Общие функции битовой маски
Биты маскировки в 1
Пример: Маскировка на чем выше полубайте (биты 4, 5, 6, 7) нижняя часть байта (биты 0, 1, 2, 3) без изменений.
Биты маскировки в 0
Пример: Маскировка от высших полубайт (биты 4, 5, 6, 7) нижней части байта (биты 0, 1, 2, 3) без изменений.
Запрос статуса бита
Пример: запрос состояния 4-го бита
Переключение битовых значений
Пример: переключение битовых значений
Чтобы записать произвольные единицы и нули в подмножество битов, сначала запишите 0 в это подмножество, а затем установите старшие биты:
Использование битовых масок
Аргументы к функциям
Тогда вызов функции выглядит так
Внутренне функция, принимающая подобное битовое поле, может использовать двоичный файл and для извлечения отдельных битов. Например, реализация glClear() может выглядеть так:
Обратные маски
сетевой адрес (трафик, который нужно обработать): 192.0.2.0
сетевой адрес (двоичный): 11000000.00000000.00000010.00000000
маска (двоичная): 00000000.00000000.00000000.11111111
Исходный / исходный-подстановочный знак 0.0.0.0 / 255.255.255.255 означает «любой».
Источник / подстановочный знак 198.51.100.2 / 0.0.0.0 совпадает с «хостом 198.51.100.2 «
Маски изображения
Хотя прозрачные цвета и альфа-каналы связаны (поскольку используются для одних и тех же целей), это методы, которые не включают смешение пикселей изображения путем двоичного маскирования.
Хеш-таблицы
Пример как по модулю, так и маскировки в C: