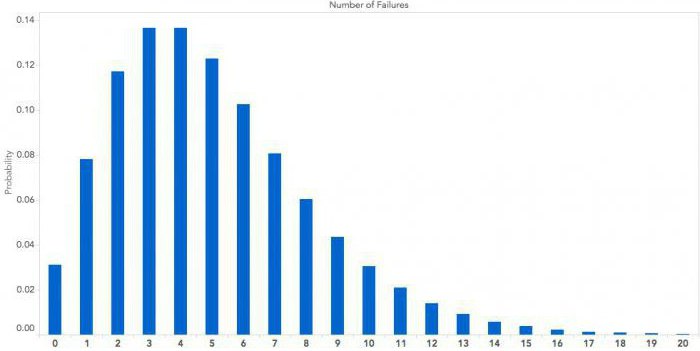
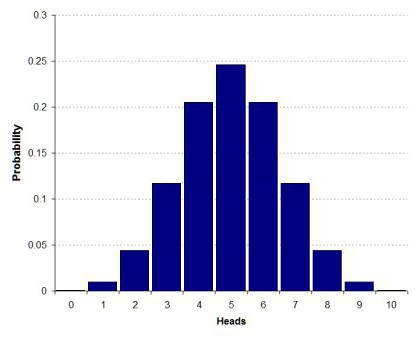
что такое биноминальное распределение
Биномиальное распределение и его предельные формы
Методические указания и примерная программа проведения лабораторной работы (практического занятия) в среде MathCad по курсу “Теория вероятностей и математическая статистика”
1. Основные положения.
Любое случайное событие удобно описывать с помощью специальной случайной величины – индикатора события ( I ). Индикатор события – это такая случайная величина, которая принимает значение, равное единице, если событие произошло и значение, равное нулю, если событие не произошло.
Видно, что А i можно рассматривать как последовательность, состоящую из m единиц и n – m нулей. Вероятность такого события равна произведению вероятностей появления события ровно m раз и его непоявления n – m раз:
При больших n и m вычисления факториалов вычисляются приближенно по формуле Стирлинга ( 1730 г.):
( при n = 10 относительная погрешность вычислений не превышает 0.83%).
Окончательно, вероятность того, что в серии из n испытаний событие произойдет ровно m раз будет равно:
Поскольку p + q = 1, то
Эта формула просто иллюстрирует аксиому теории вероятностей, cогласно которой вероятность достоверного события равна единице. Действительно, события
составляют полную группу событий.
Тогда интервал ее возрастания ( Q > 1) определится неравенством:
а интервал убывания ( Q
Положение максимума функции m* будет определяться соотношением:
2. Числовые характеристики биномиального распределения.
По определению, математическое ожидание случайной величины вычисляется по формуле:
Для закона распределения случайной величины ( 1 ) мы получим:
Биномиальное распределение
Материал из MachineLearning.
Функция вероятности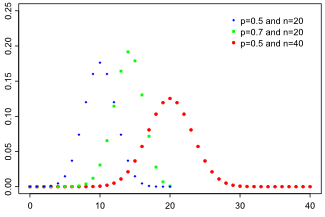 | |
Функция распределения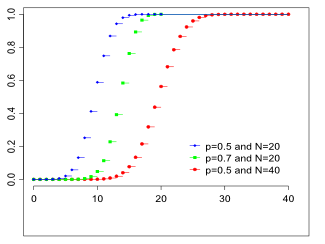 | |
| Параметры | — число «испытаний» — вероятность «успеха» |
| Носитель | |
| Функция вероятности | |
| Функция распределения | |
| Математическое ожидание | |
| Медиана | одно из |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Информационная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
Содержание
Определение
Биномиальное распределение — дискретное распределение вероятностей случайной величины принимающей целочисленные значения с вероятностями:
Данное распределение характеризуется двумя параметрами: целым числом 0,» alt= «n>0,» /> называемым числом испытаний, и вещественным числом называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из независимых испытаний, в каждом из которых может произойти «успех» с вероятностью то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы независимых слагаемых, имеющих распределение Бернулли.
Основные свойства
Асимптотические приближения при больших
Если значения велики, то непосредственное вычисление вероятностей событий, связанных с данной случайной величиной, технически затруднительно. В этих случаях можно использовать приближения биномиального распределения распределением Пуассона и нормальным (приближение Муавра-Лапласа).
Приближение Пуассона
Приближение распределением Пуассона применяется в ситуациях, когда значения большие, а значения близки к нулю. При этом биномиальное распределение аппроксимируется распределением Пуассона с параметром
Строгая формулировка: если и таким образом, что то
Более того, справедлива следующая оценка. Пусть — случайная величина, имеющая распределение Пуассона с параметром Тогда для произвольного множества справедливо неравенство:
Доказательство и обзор более точных результатов, касающихся точности данного приближения, можно найти в [1, гл. III, §12].
Нормальное приближение
Приближение нормальным распределением используется в ситуациях, когда а фиксировано. Это приближение можно рассматривать как частный случай центральной предельной теоремы, применение которой основано на представлении в виде суммы слагаемых. Приближение основано на том, что при указанных условиях распределение нормированной величины
близко к стандартному нормальному.
Локальная теорема Муавра-Лапласа
Данная теорема используется для приближенного вычисления вероятностей отдельных значений биномиального распределения. Она утверждает [1, гл. I, §6], что равномерно по всем значениям таким что имеет место
где — плотность стандартного нормального распределения.
Интегральная теорема Муавра-Лапласа
На практике необходимость оценки вероятностей отдельных значений, которую дает локальная теорема Муавра-Лапласа, возникает нечасто. Гораздо более важно оценивать вероятности событий, включающих в себя множество значений. Для этого используется интегральная теорема, которую можно сформулировать в следующем виде [1, гл. I, §6]:
где случайная величина имеет стандартное нормальное распределение и аппроксимирующая вероятность определяется по формуле
где — функция распределения стандартного нормального закона:
Есть ряд результатов, позволяющих оценить скорость сходимости. В [1, гл. I, §6] приводится следующий результат, являющийся частным случаем теоремы Берри-Эссеена:
где — функция распределения случайной величины На практике решение о том, насколько следует доверять нормальному приближению, принимают исходя из величины Чем она больше, тем меньше будет погрешность приближения.
Заметим, что асимптотический результат не изменится, если заменить строгие неравенства на нестрогие и наоборот. Предельная вероятность от такой замены также не поменяется, так как нормальное распределение абсолютно непрерывно и вероятность принять любое конкретное значение для него равна нулю. Однако исходная вероятность от такой замены может измениться, что вносит в формулу некоторую неоднозначность. Для больших значений изменение будет невелико, однако для небольших это может внести дополнительную погрешность.
Для устранения этой неоднозначности, а также повышения точности приближения рекомендуется задавать интересующие события в виде интервалов с полуцелыми границами. При этом приближение получается точнее. Это связано с тем интуитивно понятным соображением, что аппроксимация кусочно-постоянной функции (функции распределения биномиального закона) с помощью непрерывной функции дает более точные приближения между точками разрыва, чем в этих точках.
Пример
Точная вероятность рассматриваемого события равна
Применим нормальное приближение с той расстановкой неравенств, которая дана выше (снизу строгое, сверху нестрогое):
Теперь построим приближение, используя интервал с концами в полуцелых точках:
Ошибка приближения равна — примерно в 5 раз меньше, чем в предыдущем подходе.
Литература
1. Ширяев А.Н. Вероятность. — М.: МЦНМО, 2004.
Биномиальный закон распределения
Краткая теория
Для биномиального распределения известны готовые формулы для математического ожидания и дисперсии:
$$M(X)=np, \quad D(X)=npq, \quad \sigma(X)=\sqrt
А теперь перейдем к примерам и разберем «на пальцах», что за испытания и события имеются в виду, и как применять формулы, приведенные выше.
Примеры решенных задач
Задача 1. В городе 4 коммерческих банка. У каждого риск банкротства в течение года составляет 20%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года.
Задача 2. Контрольная работа состоит из трех вопросов. На каждый вопрос приведено четыре варианта ответа, один из которых правильный. Составить закон распределения числа правильных ответов при простом угадывании. Найти M(X), D(X).
Задача 4. Наблюдение за районом осуществляется тремя радиолокационными станциями (РЛС). В район наблюдений попал объект, который обнаруживается любой радиолокационной станцией с вероятностью 0,2.
Построить ряд распределения, найти функцию распределения, математическое ожидание и среднее квадратичное отклонение числа РЛС, обнаруживших объект.
Найти вероятность того, что их будет не менее двух.
Задача 6. Стрелок производит 4 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,3. За каждое попадание стрелку засчитывается 10 очков. Найти закон распределения числа засчитанных очков.
Задача 7. Опыт состоит из трех независимых подбрасываний одновременно трех монет, каждая из которых с одинаковой вероятностью падает гербом или цифрой вверх.
Построить ряд распределения, найти функцию распределения, математическое ожидание и среднее квадратичное отклонение числа одновременного выпадения двух гербов.
Найти вероятность того, что два герба одновременно выпадут хотя бы один раз.
Задача 10. Производится три независимых опыта, в каждом из которых событие А появляется с вероятностью 0,6. Построить ряд распределения и функцию распределения случайной величины X числа появления события А в трех опытах. Найти числовые характеристики этой случайной величины X.
Решебник по терверу
Нужны еще решения? Более 11000 подробно решенных и оформленных задач. Найди в решебнике сейчас:
Биномиальное распределение
Sep 9, 2019 · 5 min read
Все знают и любят нормальное распределение. Оно используется в инвестиционном моделировании, A/B-тестах и улучшении производственных процессов (шесть сигм). Но мало кто хорошо знаком с биномиальным распределением. Между тем, результаты бросков монеты следуют биномиальному распределению.
Важно, что здесь работает закон больших чисел. Я также должен сказать, что если мы многократно выполняем один и тот же набор экспериментов (подбрасывая монетку 10 раз) снова и снова, то число решек, наблюдаемых во всех экспериментах, следует биномиальному распределению.
Биномиальное распределение
Дадим более техническое определение. Биномиальное распределение — это распределение вероятностей в последовательности экспериментов, где эксперимент даёт двоичный результат. При этом результаты независимы друг от друга.
Бр о сок монеты — эксперимент с бинарным результатом. Для ясности уточню: результаты не обязательно должны быть одинаково вероятными, как с бросками симметричной монеты. Условия ниже также соответствуют предварительным требованиям биномиального распределения:
Одна вещь, которая может смутить новичков в теории вероятности и статистике — идея распределения. Мы склонны мыслить детерминистически: «Я подбросил монету 10 раз и получил 6 решек». Результат — 6. Где же распределение?
Распределение происходит из дисперсии. Если мы подбросим 10 монет, то, вероятно, получим разные результаты. Эта дисперсия (неопределенность) создает распределение. Оно сообщает, какие результаты вероятнее, а какие — нет.
Прежде чем писать симуляцию, определимся с переменными.
Симуляция на Python
Генерируем случайное число n раз и записываем результаты в списки. Если число равно 0,5 или больше, то считать его решкой, если нет — орлом. И повторим это много раз, в нашем примере 1000.
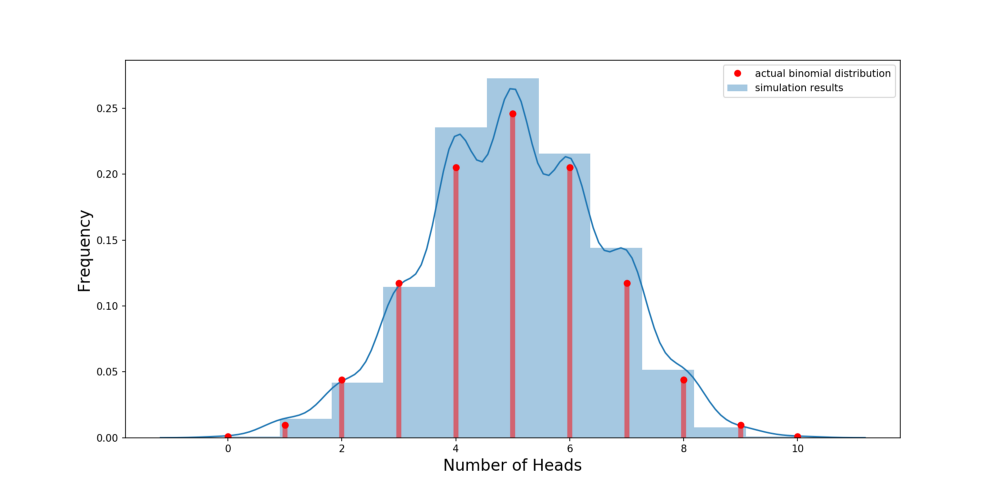
Результат выполнения кода на гистограмме:
Изменим график так, чтобы он отображал распределение. Используем stats.binom из scipy :
На графике ниже показано моделируемое распределение синим цветом и фактическое — красным. Вывод: биномиальное распределение — достаточно хорошее приближение к реальности. Поэтому вместо того, чтобы тратить время на подбрасывание и записывать результаты, мы можем просто использовать биномиальное распределение!
Если мы хотим смоделировать результат последовательности из n экспериментов, то могли бы сделать это, используя биномиально распределенную случайную переменную, например:
Наконец, ответим на наш вопрос о монетках:
Это также соответствует первой гистограмме.
Реалистичный пример
Хорошо, а есть что-то кроме монет? Конечно! Представьте себе, что мы аналитики, которым поручено повышение возврата инвестиций в call-центр компании. Сотрудники звонят потенциальным клиентам и продают продукт. Вы посмотрели исторические данные и обнаружили:
Выполнив код, вы увидите что-то вроде этого:
Прибыль в сравнении с расходами невелика. Но посмотрим, как изменяется дневной доход на 1000 симуляций.
Высока вероятность потерь. Что делать? Результаты каждого сотрудника соответствуют биномиальному распределению, поэтому вот, что можно сделать:
Нам не нужен A/B-тест, чтобы понять, что прибыли будет больше. Красная гистограмма — результат после улучшений.
Распределение биномиальное: определение, формула, примеры
Прежде чем перейти непосредственно к математике и теории вероятности, разберёмся с тем, кто же первый придумал такой вид распределения и какова история развития математического аппарата для этого понятия.
История
Понятие вероятности известно ещё с древних времён. Однако древние математики не придавали ей особо значения и смогли заложить только основы для теории, ставшей впоследствии теорией вероятности. Они создали некоторые комбинаторные методы, которые сильно помогли тем, кто позже создал и развил саму теорию.
Во второй половине семнадцатого века началось формирование основных понятий и методов теории вероятности. Были введены определения случайных величин, способы вычисления вероятности простых и некоторых сложных независимых и зависимых событий. Продиктован такой интерес к случайным величинам и вероятностям был азартными играми: каждый человек хотел знать, какие у него шансы победить в игре.
Следующим этапом стало применение в теории вероятности методов математического анализа. Этим занялись видные математики, такие как Лаплас, Гаусс, Пуассон и Бернулли. Именно они продвинули эту область математики на новый уровень. Именно Джеймс Бернулли открыл биномиальный закон распределения. Кстати, как мы позже выясним, на основе этого открытия были сделаны ещё несколько, которые позволили создать закон нормального распределения и ещё множество других.
Сейчас, прежде чем начать описывать распределение биномиальное, мы немного освежим в памяти понятия теории вероятностей, наверняка уже забытые со школьной скамьи.
Основы теории вероятностей
Это было самое простое событие. Но бывают ещё и сложные системы, в которых выполняются последовательные действия, и вероятности исходов этих действий будут различаться. Например, рассмотрим такую систему: в коробке, содержимое которой мы не можем разглядеть, лежат шесть абсолютно одинаковых шариков, три пары синего, красного и белого цветов. Мы должны достать наугад несколько шариков. Соответственно, вытащив первым один из белых шариков, мы уменьшим в разы вероятность того, что следующим нам тоже попадётся белый шарик. Происходит это потому, что меняется количество объектов в системе.
В следующем разделе рассмотрим более сложные математические понятия, вплотную подводящие нас к тому, что означают слова «нормальное распределение», «биномиальное распределение» и тому подобные.
Элементы математической статистики
Математическое ожидание
На самом деле понять то, что такое математическое ожидание, несложно. Рассмотрим систему, в которой существует много разных событий со своими различными вероятностями. Математическим ожиданием будет называться величина, равная сумме произведений значений этих событий (а математическом виде, о котором мы говорили в прошлом разделе) на вероятности их осуществления.
Дисперсия биномиального распределения
В общем, это всё, что нам нужно знать о дисперсии для понимания того, что такое биномиальное распределение вероятностей. Теперь перейдём непосредственно к нашей основной теме. А именно к тому, что же кроется за таким на вид достаточно сложным словосочетанием «биномиальный закон распределения».
Биномиальное распределение
Формулы распределения
Функция биномиального распределения может быть записана в виде суммы следующих членов:
Помимо этого, функция биномиального распределения может быть записана в виде неполной бета-функции. Однако это уже более сложное определение, которое используется только при решении сложных статистических задач.
В следующем разделе рассмотрим аспекты, касающиеся применения этого математического аппарата в реальной жизни. На первый взгляд, конечно, кажется, что это очередная математическая штука, которая, как обычно, не находит применения в реальной жизни, и вообще не нужна никому, кроме самих математиков. Однако это далеко не так. Ведь все виды распределений и их графические представления были созданы исключительно под практические цели, а не в качестве прихоти учёных.
Применение
Безусловно, самое важное применение распределения находят в статистике, ведь там нужен комплексный анализ множества данных. Как показывает практика, очень многие массивы данных имеют примерно одинаковые распределения величин: критические области очень низких и очень высоких величин, как правило, содержат меньше элементов, чем средние значения.
Анализ больших массивов данных требуется не только в статистике. Он незаменим, например, в физической химии. В этой науке он используется для определения многих величин, которые связаны со случайными колебаниями и перемещениями атомов и молекул.
В следующем разделе разберёмся, насколько важно применение таких статистических понятий, как биномиальное распределение случайной величины в повседневной жизни для нас с вами.
Зачем мне это нужно?
Многие задают себе такой вопрос, когда дело касается математики. А между прочим, математика не зря называется царицей наук. Она является основой физики, химии, биологии, экономики, и в каждой из этих наук применяется в том числе и какое-либо распределение: будь это дискретное биномиальное распределение, или же нормальное, не важно. И если мы получше присмотримся к окружающему миру, то увидим, что математика применяется везде: в повседневной жизни, на работе, да даже человеческие отношения можно представить в виде статистических данных и провести их анализ (так, кстати, и делают те, кто работают в специальных организациях, занимающихся сбором информации).
Сейчас поговорим немного о том, что же делать, если вам нужно знать по данной теме намного больше, чем то, что мы изложили в этой статье.
Что ещё можно почитать?
Та информация, что мы дали в этой статье, далеко не полная. Существует множество нюансов, касаемо того, какую форму может принимать распределение. Биномиальное распределение, как мы уже выяснили, является одним из основных видов, на котором зиждется вся математическая статистика и теория вероятностей.
Заключение
Прежде чем закончить статью, мы хотели бы рассказать ещё одну интересную вещь. Она касается непосредственно темы нашей статьи и всей математики в целом.
Итак, мы рассмотрели понятие биномиального распределения и все связанные с ним определения и поговорили о том, как же это применяется в нашей с вами жизни.