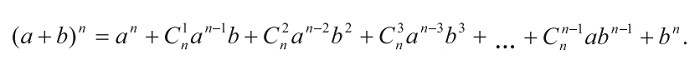что такое бином человека
Значение слова «бином»
[От лат. bis — дважды и греч. νόμος — часть, отдел]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Для вычисления степеней биномов используется бином Ньютона. Например, в случае второй степени:
Также используются формулы
бино́м
1. матем. алгебраическое выражение, представляющее сумму или разность двух одночленов
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова мизантропия (существительное):
Синонимы к слову «бином»
Предложения со словом «бином»
Цитаты из русской классики со словом «бином»
Сочетаемость слова «бином»
Понятия, связанные со словом «бином»
Отправить комментарий
Дополнительно
Предложения со словом «бином»
Для языков этого типа характерна ситуация, когда в тексте основной структурной единицей выступает бином– двусложное слово или двусложная же словоподобная единица.
Именно в этом и состоит бином «личность – общность», требующий результативной, то есть совершенной, слаженности.
Я добавил бы такой тип бинома, как степь, хотя он тоже трактуется чрезвычайно широко и подразумевает большое разнообразие местностей, растительности, высот над уровнем моря и климата.
БИНОМ
Полезное
Смотреть что такое «БИНОМ» в других словарях:
бином — а, м. binôme, лат. binomia m. 1. мат. Алгебраическое выражение, представляющее сумму или разность одночленов; двучлен. БАС 2. Боюсь, еслиб я и осмелился представить здесь самое простое развитие двучленника (бинома) Ньютонова необходимого для сего … Исторический словарь галлицизмов русского языка
Бином — (лат. bis дважды, nomen имя) или двучлен частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например: Для вычисления степеней биномов используется бином Ньютона: А также … Википедия
бином — двучлен Словарь русских синонимов. бином сущ. • двучлен Словарь русских синонимов. Контекст 5.0 Информатик. 2012. бином … Словарь синонимов
БИНОМ — (от би. и лат. nomen имя) то же, что двучлен. О биноме вида (x+y)n см. в ст. Ньютона бином … Большой Энциклопедический словарь
бином — БИНОМ, а, м. (или бином ньютона). Ирон. О чем л. кажущемся сложным, запутанным. Возм. распространилось под влиянием романа М. Булгакова «Мастер и Маргарита» … Словарь русского арго
Бином ПМ-2 — (ТУ5730 001 96360128 2007) – соответствует требованиям для пластифицирующих водоредуцирующих и противоморозных добавок. Обеспечивает протекание процессов гидратации цемента при температуре твердения бетона не ниже минус 18°С. Не… … Энциклопедия терминов, определений и пояснений строительных материалов
БИНОМ — сумма или разность двух одночленов. Бином Ньютона формула, выражающая произвольную натуральную степень Б. в виде многочлена, расположенного по степеням одного из членов Б … Большая политехническая энциклопедия
БИНОМ — (от би. и латинского nomen имя) (двучлен), алгебраическая сумма двух одночленов … Современная энциклопедия
БИНОМ — БИНОМ, а, муж. В математике: двучлен. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
БИНОМ — муж. биномия жен. в буквосчислении: численное выражение, состоящее из двух членов; двучлен, двучленная величина. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
Бином – что означает? Определение, значение, примеры употребления
Ищешь, что значит слово бином? Пытаешься разобраться, что такое бином? Вот ответ на твой вопрос:
Значение слова «бином» в словарях русского языка
Бином это:
бином ( — дважды, — имя) или двучлен — частный случай полинома (многочлена), состоящего из двух слагаемых мономов (одночленов). Например:
Для вычисления степеней биномов используется бином Ньютона.
Бином
Бином
Бином
м. Алгебраическое выражение, представляющее сумму или разность двух одночленов; двучлен (в математике).
Бином
муж. биномия жен. в буквосчислении: численное выражение, состоящее из двух членов; двучлен, двучленная величина.
Бином
[би… + гр. nome доля, часть]мат. двучлен — алгебраическое выражение, представляющее собой сумму или разность двух одночленов (ср. моном, полином); б. ньютона — формула, представляющая степень некоторого двучлена в виде суммы (разложение бинома):
Бином
Бином
В математике: двучлен
Бином
(от би … и лат. nomen — имя), то же, что двучлен. О биноме вида (x+y)n см. в ст. Ньютона бином.
Бином
бином м. Алгебраическое выражение, представляющее сумму или разность двух одночленов; двучлен (в математике).
Бином
Бином
Бином
Бином
алгебраическое выражение, представляющее сумму или разность двух одночленов
Бином
Бином
Бином
Бином
Бином
Бином
Бином
Бином
Где и как употребляется слово «бином»?
Кроме значения слова «бином» в словарях, рекомендуем также ознакомиться с примерами предложений и цитат из классической литературы, в которых употребляется слово «бином».
Так вы сможете гораздо легче понять и запомнить, как правильно употребляется слово «бином» в тексте и устной речи.
Примеры употребления слова «бином»
Для языков этого типа характерна ситуация, когда в тексте основной структурной единицей выступает бином – двусложное слово или двусложная же словоподобная единица.
Именно в этом и состоит бином «личность – общность», требующий результативной, то есть совершенной, слаженности.
Бином Ньютона
В художественной литературе бином Ньютона часто упоминается, когда речь идет о чем-либо сложном. Автор этой формулы — великий физик и математик Исаак Ньютон. Дело не только в том, что формула кажется сложной. Изучение ее то включали в программу средней школы, то выводили за рамки основного курса, но в серьезных вузах экзаменаторы спрашивали и продолжают спрашивать о биноме Ньютона.
Бином Ньютона — формула разложения произвольной натуральной степени двучлена в многочлен. Каждый из нас знает наизусть формулы квадрата суммы, но при увеличении показателя степени возникают трудности с определением коэффициентов при членах многочлена. Чтобы не совершить ошибку, можно применять формулу бинома Ньютона:
Левое число — степень n, справа — значения соответствующих биномиальных коэффициентов.
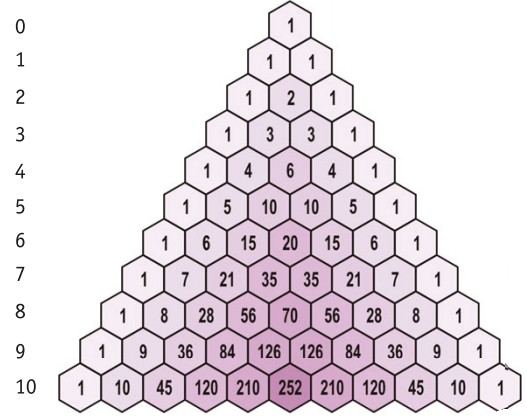
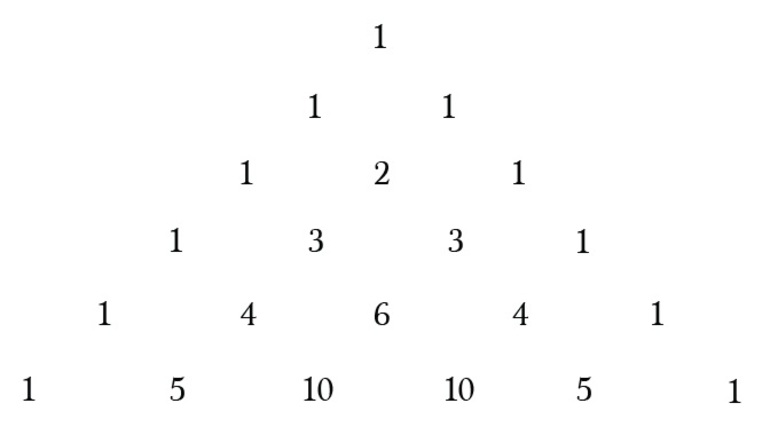
Все очень просто и запоминается на всю жизнь. Кстати, самостоятельно вспомнить и вывести формулу бинома Ньютона, нарисовав треугольник Паскаля, тоже намного проще.
Ряд историков науки приписывают Паскалю авторство не только треугольника, позволяющего находить биномиальные коэффициенты, но и самой формулы бинома. Они считают, что Паскаль вывел ее несколько раньше Ньютона, а тот лишь обобщил формулу для разных показателей степеней.
Древние знания
Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.
Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.
Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.
Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.
Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:
К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.
Утверждение теоремы
Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.
Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :
Теорема может быть применена к степеням любого бинома.
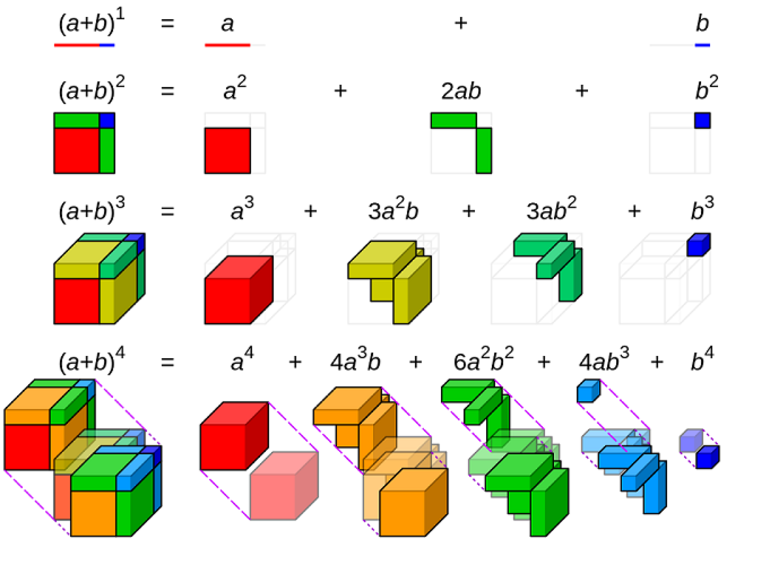
С точки зрения геометрии
Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.
Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:
Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.
Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.
Биномные обобщения
Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.
Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.
Короткий путь
Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.
Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).
Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.