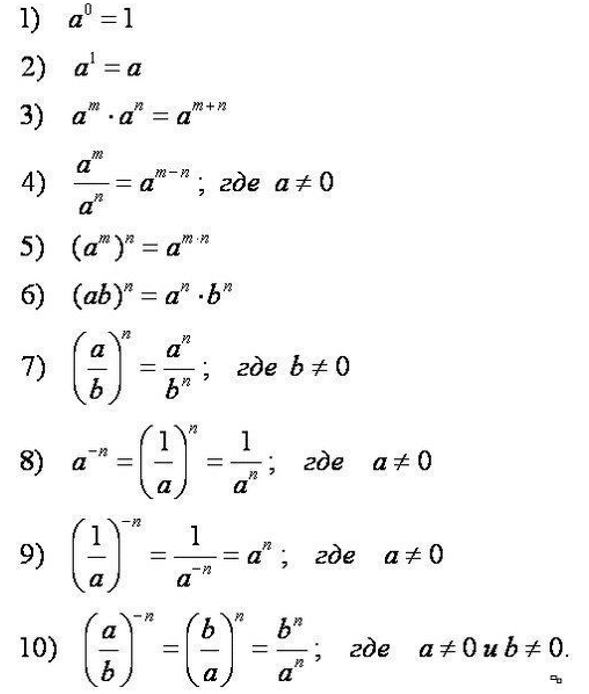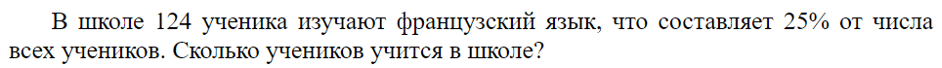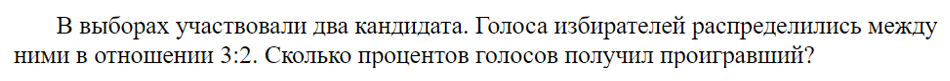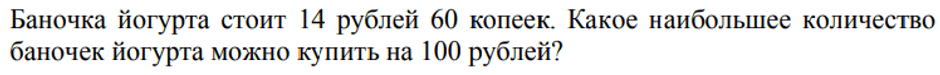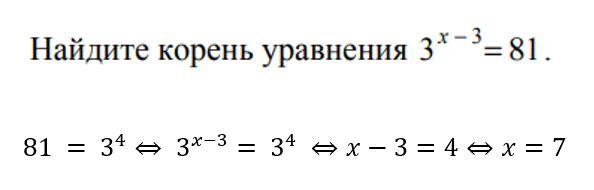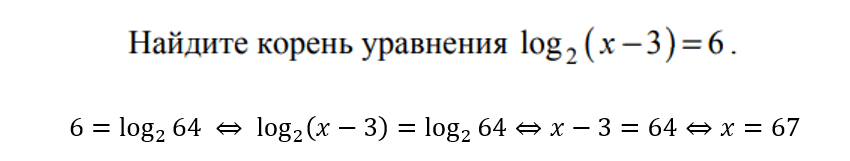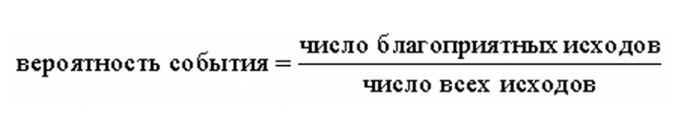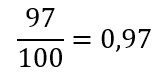что такое базовая математическая подготовка
СТАНДАРТ СРЕДНЕГО (ПОЛНОГО) ОБЩЕГО ОБРАЗОВАНИЯ
ПО МАТЕМАТИКЕ
БАЗОВЫЙ УРОВЕНЬ
Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:
· формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
· развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;
· овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
· воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.
ОБЯЗАТЕЛЬНЫЙ МИНИМУМ СОДЕРЖАНИЯ
ОСНОВНЫХ ОБРАЗОВАТЕЛЬНЫХ ПРОГРАММ
Основы тригонометрии. Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. Основные тригонометрические тождества. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. Преобразования суммы тригонометрических функций в произведение и произведения в сумму. Выражение тригонометрических функций через тангенс половинного аргумента. Преобразования простейших тригонометрических выражений.
Арксинус, арккосинус, арктангенс числа.
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях.
Обратная функция. Область определения и область значений обратной функции. График обратной функции.
Степенная функция с натуральным показателем, ее свойства и график.
Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций.
Тригонометрические функции, их свойства и графики; периодичность, основной период.
Показательная функция (экспонента), ее свойства и график.
Логарифмическая функция, ее свойства и график.
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Понятие о пределе последовательности. Существование предела монотонной ограниченной последовательности. Длина окружности и площадь круга как пределы последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.
Понятие о непрерывности функции.
Понятие об определенном интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница.
Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономи-ческих, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл.
УРАВНЕНИЯ И НЕРАВЕНСТВА
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ
Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля.
Прямые и плоскости в пространстве. Основные понятия стереометрии (точка, прямая, плоскость, пространство).
Пересекающиеся, параллельные и скрещивающиеся прямые. Угол между прямыми в пространстве. Перпендикулярность прямых. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная. Угол между прямой и плоскостью.
Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла.
Расстояния от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми.
Параллельное проектирование. Площадь ортогональной проекции многоугольника. Изображение пространственных фигур.
Призма, ее основания, боковые ребра, высота, боковая поверхность. Прямая и наклонная призма. Правильная призма. Параллелепипед. Куб.
Симметрии в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая, зеркальная). Примеры симметрий в окружающем мире.
Сечения куба, призмы, пирамиды.
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).
Тела и поверхности вращения. Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию.
Шар и сфера, их сечения, касательная плоскость к сфере.
Объемы тел и площади их поверхностей. Понятие об объеме тела. Отношение объемов подобных тел.
Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Угол между векторами. Координаты вектора. Скалярное произведение векторов. Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам. Компланарные векторы. Разложение по трем некомпланарным векторам.
ТРЕБОВАНИЯ К УРОВНЮ
ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики на базовом уровне ученик должен
· значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
· значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
· универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
· вероятностный характер различных процессов окружающего мира;
· выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
· проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
· вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
· практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
· определять значение функции по значению аргумента при различных способах задания функции;
· строить графики изученных функций;
· описывать по графику и в простейших случаях по формуле [3] поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
· решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
· описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
Начала математического анализа
· вычислять производные и первообразные элементарных функций, используя справочные материалы;
· исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
· вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
· решения прикладных задач, в том числе социально-экономи-ческих и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
· решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы ;
· составлять уравнения и неравенства по условию задачи;
· использовать для приближенного решения уравнений и неравенств графический метод;
· изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
· построения и исследования простейших математических моделей;
Элементы комбинаторики, статистики и теории вероятностей
· решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
· вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
· анализа реальных числовых данных, представленных в виде диаграмм, графиков;
· анализа информации статистического характера;
· распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
· описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении ;
· анализировать в простейших случаях взаимное расположение объектов в пространстве;
· изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
· строить простейшие сечения куба, призмы, пирамиды ;
· решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
· использовать при решении стереометрических задач планиметрические факты и методы;
· проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
· исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
· вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
[1] Курсивом в тексте выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников.
[2] Помимо указанных в данном разделе знаний, в требования к уровню подготовки включаются также знания, необходимые для освоения перечисленных ниже умений.
[3] Требования, выделенные курсивом, не применяются при контроле уровня подготовки выпускников профильных классов гуманитарной направленности.
Требования к содержанию и уровню математической подготовки детей дошкольного возраста
Юлиана Кожурова Гаврильевна
Требования к содержанию и уровню математической подготовки детей дошкольного возраста
Методическая папка на тему: «Требования к содержанию и уровню математической подготовки детей дошкольного возраста»
Содержание:
3. Требования к содержанию и уровню математической подготовки детей дошкольного возраста.
1. Понятие преемственности в математическом развитии детей ДОУ и школы.
2. Показатели готовности детей к изучению математики в первом классе.
Требования к содержанию и уровню математической подготовки детей дошкольного возраста
Вхождение детей в мир математики начинается уже в дошкольном возрасте. Математика является универсальным методом познании окружающего и предметного мира и ее роль в современной науке постоянно возрастет. Изменение концептуальных подходов к определению содержания и выбору методик обучения математике в школе, широкое использование современных образовательных технологий обусловило и требования к математической подготовке детей дошкольного возраста.
Сегодня «Математика – это больше, чем наука, это – язык». Математика является универсальным и мощным методом познания. Изучение математики совершенствует общую культуру мышления, приучает детей логически рассуждать, воспитывает у них точность обстоятельность высказываний. Она развивает такие интеллектуальные качества, как способность к абстрагированию, общению, способность мыслить анализировать, критиковать. Упражнение математикеспособствует приобретению рациональных качеств мысли и ее выражение: порядок, точность, ясность,сжатость: требует выражение интуиции.
После принятия ФГОС ДО, основополагающего документа, регламентирующего деятельность дошкольных образовательных организаций, наступил достаточно сложный период. В первую очередь в сложной ситуации оказались воспитатели, которые должны реализовать положения Стандарта и перестроить образовательный процесс в соответствии с целями, задачами, обозначенными в качестве приоритетных в данном документе.
Область «Познавательное развитие» Элементарные математические представления
— предполагает развитие интересов и познавательной мотивации;
— формирование познавательных действий,становление сознания:
— развития воображения и творческой активности:
— формирование первичных представлений о себе, других людях, объект окружающего мира
Программное содержание раздела «Формирование элементарных математических представлений» должно быть «вплетено» в образовательный процесс и реализовываться через привлекательные виды детской деятельности.
Система обучения в детском саду была построена таким образом, что каждое занятие строго регламентировано по времени, и по месту и по частоте. Дети привыкают воспринимать математику как занятие, которое бывает 1-2 раза в неделю.
Дошкольник всегда должен видеть и воспринимать применяемость своих знаний и умений значимой для него деятельности.
В качестве таковой могут выступать:
3. детское экспериментирование, конструктивная деятельность любых видов,
4. художественно – изобразительная и музыкально – двигательная деятельность,
5. литературно – языковая деятельность, общение, физическая двигательная деятельность и разнообразная трудовая деятельность.
Например: при знакомстве с геометрическими фигурами мы обращаем внимание на метрическую структуру каждой из них (наличие сторон, углов, вершин, объема и пр). Зная эти характерные особенности, ребенок сможет отличать геометрические фигуры, правильно их дифференцировать и обобщать по ключевым признакам. С этой целью мы можем предъявлять детям геометрические фигуры не в стандартном общепринятом виде, а со сдвигом оси.
Таким образом, и будут решаться приоритетные задачи непрерывного образования детей.
Вывод: таким образом, можно выделить следующие требования к математическому развитию детей: развитие познавательных интересов; интеллектуального развитие; развитие исследовательской деятельности ребенка; развитие умения анализировать; развитие умения устанавливать ассоциативные связи; развитие логического мышления, а именно умения устанавливать простейшие закономерности; формирование предпосылок учебной деятельности.
Понятие преемственности в математическом развитии детей ДОУ и школы
Создание единой системы воспитания и образования подрастающего поколения предусматривает неразрывную связь, логическую преемственность в работе всех звеньев этой системы, в данном случае в детском саду и школе.
Обучение дошкольников как начальное звено образования ориентируется на возможности детей этого возраста, а также на требования современного начального обучения. Оба эти условия определяют содержание, организационные формы, методы и средства обучения.
Дети учатся обозначать размеры предметов непосредственно сравнением, а также с помощью измерений условной мерой и линейкой, чертить отрезки определенной длины.Они знакомятся с многоугольниками и их элементами: сторонами, углами, вершинами, должны уметь свободно ориентироваться на листе бумаги, в тетради, книге, во времени и в окружающем пространстве.
Однако современную школу не удовлетворяет формальное усвоение этих знаний и умений. Дальнейшее обучение в школе обычно зависимо от качества усвоенных знаний, их осознанности, гибкости и прочности. Поэтому современная дошкольная дидактика направлена на отработку путей оптимизации обучения с целью повышения этих качеств. Выпускники дошкольных учреждений должны осознанно, с пониманием сути явлений уметь использовать приобретенные знания и навыки не только в обычной, стереотипной, но и в измененной ситуации, в новых, необычных обстоятельствах (игра, труд).
Одно из главных требований начального обучения к математической подготовке заключается в дальнейшем развитии мышления дошкольников. Математика — это глубоко логическая наука. Введение ребенка даже в начальную элементарную математику абсолютно невозможно без достаточного уровня развития логического мышления.
Таким образом, достижение высокого уровня готовности детей к обучению в школе предусматривает усовершенствование прежде всего содержания, форм и методов учебно-воспитательной работы в детском саду, в частности в обучении их математике.
Показатели готовности детей к изучению математики в первом классе
Сформировать готовность к обучению в школе означает создать условия для успешного усвоения детьми учебной программы и нормального вхождения их в ученический коллектив. Одним из важных показателей специальной (математической)готовности является наличие у дошкольников определенных знаний, умений и навыков. Как показывает анализ педагогической работы, уровень усвоения этих знаний, умений и навыков зависит от возраста, индивидуальных особенностей детей, а также от состояния учебно-воспитательного процесса в детском саду.
Для воспитателя подготовительной группы особое значение приобретает выявление этого уровня перед поступлением детей в школу. Этому способствуют индивидуальные беседы, дидактические игры и упражнения с детьми, выполнение ими специальных заданий и т. д.При этом следует ориентироваться на такие показатели:
• объем математических знаний и умений в соответствии с программой воспитания в детском саду;
• качество математических знаний: осознанность, прочность, запоминание, возможность использования их в самостоятельной деятельности;
• уровень умений и навыков учебной деятельности;
• степень развития познавательных интересов и способностей;
• особенности развития речи (усвоение математической терминологии);
• положительное отношение к школе и учебной деятельности в целом;
• уровень познавательной активности.
Важный показатель при обследовании— продуктивность внимания (по адаптированным корректурным таблицам, особенности умственного развития и учебной деятельности. Индивидуальное обследование дает возможность воспитателю создать представление об особенностях речи детей, общем уровне знаний и специальной математической подготовке.
Дополнительная образовательная программа по экологии «Зернышко» для детей 6–7 лет (требования к уровню образования детей) 2.6. Иные характеристики содержания Программы Требования к уровню образования воспитанников Высокий уровень Ребёнок знает представителей.

Проблемы подготовки детей к школе в детском саду Положительное отношение к школе включает в себя как интеллектуальные, так и эмоционально-волевые компоненты, стремление занять новое социальное.

Проект «Журналисты» для детей старшего дошкольного возраста на тему «Здоровье и безопасность детей дошкольного возраста» Цель: Формирование основ безопасного поведения в быту, социуме, природе. Задачи: Закреплять умение соблюдать правила пребывания в детском.
Психологические требования к цветовому оформлению интерьера ДОУ Психологические требования к цветовому оформлению интерьера ДОУ. Дорогие мои коллеги, добрый вечер! Предлагаю вам интересную информацию.
Стихотворения для детей от 4 до 11 лет для подготовки тематики «Космическое путешествие и мечта» Здравствуйте уважаемые воспитатели и педагоги начальных классов. Современный человек не может не иметь понятия о мире космоса. Понятия начинают.
Быстро подготовиться к базовой математике — инструкция к каждому заданию
Антонина Белова
Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.
В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Их выделили пометкой «Делаем обязательно», и таких заданий 10 штук. Как раз с запасом на ошибки.
Для тех, кто хочет получить выше тройки, мы дали рекомендации по еще 4 задачкам. Итого мы рассмотрели 14 номеров. Стоит сделать их все, и твердая четверка у вас в кармане.
Научим решать сложные задания
ЕГЭ по математике
на пробном уроке в MAXIMUM
Задание 1 (Делаем обязательно!)
Задание проверяет базовые навыки счета, которым вы научились в 5-6 классах. Для получения балла надо:
Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления простых и десятичных дробей. Мы лично знаем ребят, которые не могут правильно разделить десятичные дроби в 11 классе!
Задание 2 (Делаем обязательно!)
Задача чуть сложнее: пример со степенями. Для выполнения надо:
Нужная теория будет в справочных материалах на экзамене, но это не поможет, если не наработан навык ею пользоваться. Практика обязательна.
Задание 3
Составители экзамена проверяют ваш навык работы с процентами. Задачи на проценты бывают трех типов:
Тип 1. Найти часть от числа
Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:
Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13-ю процентами. Сколько это в рублях нам еще предстоит узнать.
Чтобы ответить на вопрос задачи, делаем 3 шага:
А. Переводим процент в десятичную дробь
Для этого всегда надо количество процентов поделить на 100.
Б. Находим, сколько это от зарплаты в рублях
Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число на эту дробь умножить.
12 500 * 0,13 = 1 625 (р.) — налог, который удержат с зарплаты Ивана Кузьмича.
В. Отвечаем на вопрос задачи
У нас просили зарплату после вычета налога, а не сам налог.
12 500 — 1625 = 10 875 (р.)
Будьте внимательны, многие завалятся именно на последнем шаге!
Тип 2. Найти число по его части
Прочувствуйте разницу с прошлой задачей: тут 124 это и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.
А. Переводим процент в десятичную дробь
Б. Находим, сколько учеников всего
Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.
124 : 0,25 = 496 (у.) — всего.
Тип 3. Найти, сколько процентов часть составляет от целого
Особенность подобных заданий — не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.
А. Находим, какую долю новая цена составляет от первоначальной
Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть на целое разделить.
Б. Переводим долю в процент
В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100
0,85 * 100 = 85 % — столько процентов новая цена составляет от старой
В. Отвечаем на вопрос задачи
Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной? Конечно, изначально она была 100%. Итого
Остался последний тип, не так явно связанный с процентами…
Тип 4. Задачи на соотношение
Если чуть перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они ОДИНАКОВЫЕ по величине.
Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.
А. Считаем общее количество частей
Б. Узнаем, сколько голосов составляет одна такая часть
Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит каждая из пяти частей «весит»…
В. Отвечаем на вопрос задачи
За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
Решение этих задач удобнее всего оформить табличкой
| 1 кандидат | 2 кандидат | Всего | |
| Части | 3 | 2 | 5 |
| Абсолютные величины | 20% * 2= 40% | 100 % |
1 часть = 100% : 5 = 20%
Если рассчитываете решать текстовую задачу, включите здравый смысл! Ответ всегда можно проверить на адекватность благодаря обычной логике. Без нее и выстроить ход решения выйдет вряд ли.
Задание 4 (Делаем обязательно!)
Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:
Самое трудное тут — правильно выразить искомую величину: повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.
И да, в базе часто эта задача проста настолько, что даже перекидывать ничего не придется, нужная величина уже будет слева от равно.
Задание 5
Задачка чуть сложнее: придется поработать с выражением. Чтобы точно получить балл, надо подготовиться ко всем возможным вариантам номера. Чтобы сдать базовую математику, нужно повторить и, самое главное, научиться применять:
Да, почти вся эта теория будет у вас на экзамене в справочных материалах, но еще раз: не надейтесь грамотно ею воспользоваться без наработанного навыка.
Задание 6 (Делаем обязательно!)
Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.
Если ходите в магазин с карманными деньгами, то сталкиваетесь с подобными задачами каждый день! Разделим 100 рублей на стоимость одной упаковки йогурта. Не забываем приводить все величины к одной размерности:
Так сколько баночек йогурта вам продадут? На 7 штук вам явно не хватает денег, значит округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.
Одна пачка на 6 рулонов, значит на 63 рулона:
Но опять же, никто полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на 3 последние рулона. Значит округлить надо в большую сторону, взять клей с небольшим запасом. Снова математическое правило округления игнорируем.
Задание 7 (Делаем обязательно!)
Хотите сдать базовую математику — вам повезло! В номере с уравнениями не попадется тригонометрического. Зато могут быть..
Раскрываем скобки, если они есть, слагаемые с «х» переносим в одну сторону от равно, без «х» — в другую. Приводим подобные и решаем простейшее уравнение.
Бывают полные и неполные, всего надо повторить 3 алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.
Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений (ОДЗ): подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.
Чуть веселее. Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:
Еще чуть веселее. С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.
Тут тоже могут быть особенности с ОДЗ. Проверяйте подстановкой.
Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо икса в уравнение! Не забывайте проверять, ведь это возможность убедиться на 100%, что заветный балл не проплывет мимо. Только так можно уверенно сдать базовую математику.
Задание 9 (Делаем обязательно!)
Задача на здравый смысл. Нужно соотнести величины с их возможными значениями.
Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек 8 тонн.
Главное — внимательно перенести ответы в бланк.
Задание 10 (Делаем обязательно!)
Простая задача на определение вероятности.
Решаем с помощью формулы:
Внимательно читаем вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит остальные в порядке, и нам подойдет любая из оставшихся 97 штук. Это и есть наши благоприятные исходы из формулы.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит ответ у вас выйдет некрасивый, но вы его «причЕшите» округлением.
Еще один подвох: формулировка с предлогом «на». К примеру, «на 100 лампочек 3 неисправны, найдите вероятность купить неисправную». Подходящие исходы даны тут явно: 3 неисправные лампочки. А вот число всех исходов спрятано и составляет 103, потому что «на».
Всегда есть вероятность, что вам не повезет, и попадется задачка с перебором подходящих вариантов… Тема довольно объемная, можете изучить ее самостоятельно или надеяться на удачу.
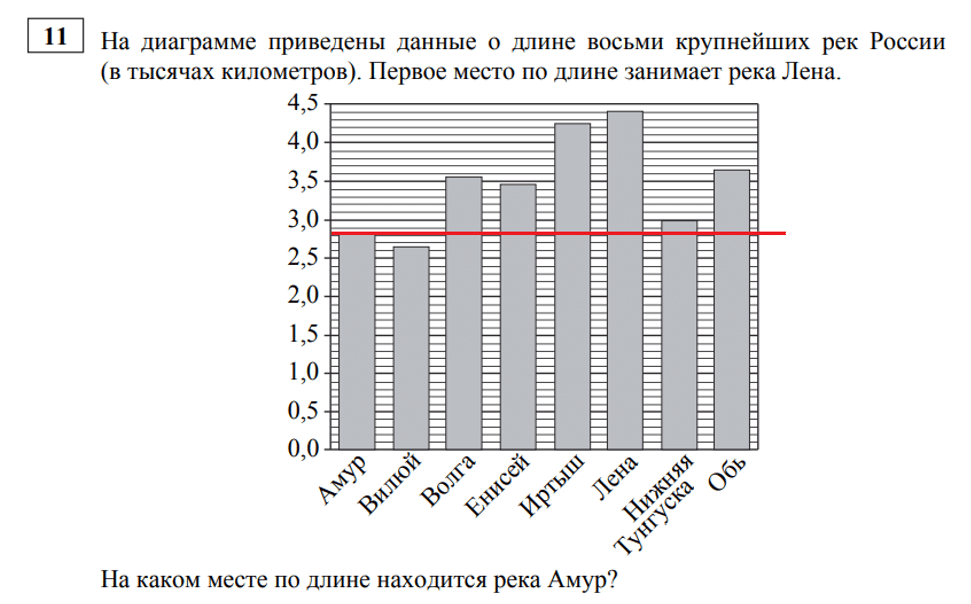
Задание 11 (Делаем обязательно!)
Задание на работу с графиком, диаграммой или таблицей, и не выполнить его вы просто не имеете права! Вооружайтесь карандашом, читайте условие с предельной внимательностью, безжалостно отмечайте нужные по условию значения на картинке в КИМе. Мы серьезно, вы и представить не можете, сколько народу теряет тут баллы по невнимательности.
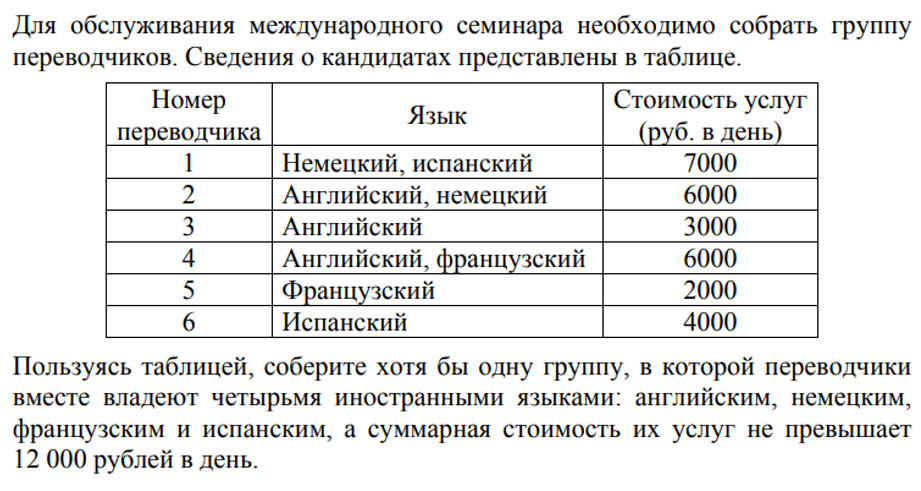
Задание 12 (Делаем обязательно!)
Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.
Задание 14
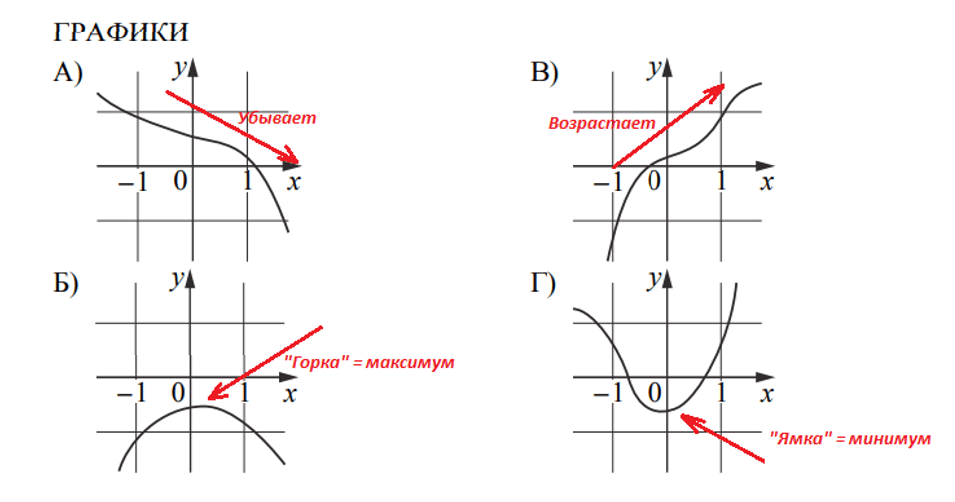
В номере точно понадобится навык анализа поведения функции по графику.
Запомним: точка максимума будет на «горке». Точка минимума — в«ямке». Функция убывает, если идёт вниз слева направо. Возрастает, если идёт вверх слева направо.
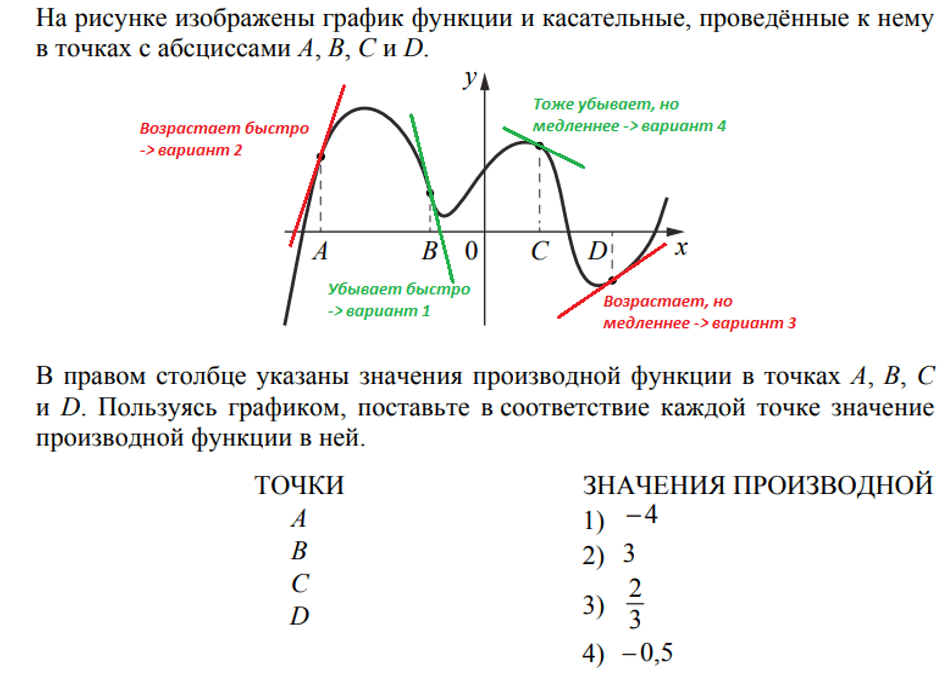
Если не повезет, то придется вспомнить азы теории по производной.
Здесь всё дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает – отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.
Задание 18 (Делаем обязательно!)
Задача проверяет у ребят, которые хотят сдать базовую математику, умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.
Все, что от вас требуется – схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.
Важно! Не додумывайте какие-то дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.
А бывают случаи, когда с визуализацией задачки придется постараться.
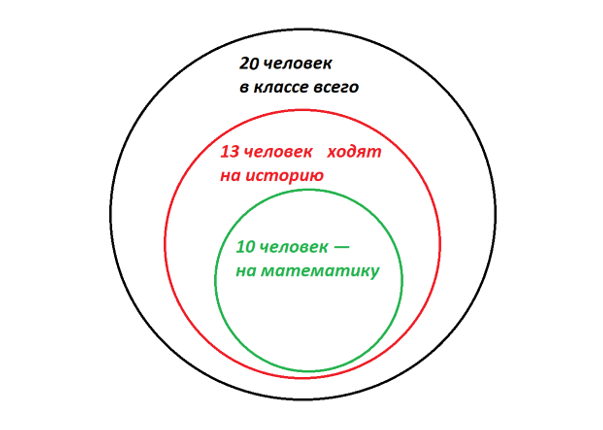
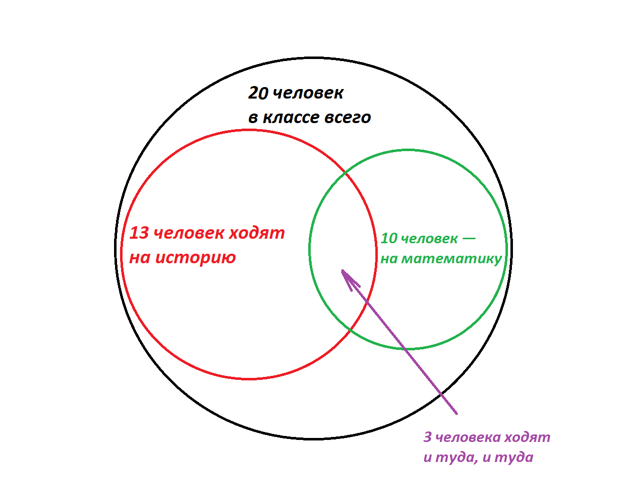
Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам?
Конечно, возможны еще какие-то промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
Так что для решения иногда мало логики, понадобится еще чуток воображения. Потренируйтесь, и ваши шансы получить балл повысятся.
Задание 19
Чем дальше, тем интереснее становятся задачи. Этот номер уже напоминает олимпиадную задачку, правда для средней школы.
Если хотите сдать базовую математику и решить 19 номер, надо немного познакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте, если время на ЕГЭ позволяет.
Например, тут нам помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на разные множители, признак для которых есть. Например, это:
Эти несложные закономерности гугл выдает по первому же запросу. Их немного: на 2, 3, 4, 5, 8, 9, 10, 11. Вполне посильная задача для выпускника.
Начнем с признака для четырех. Пока что наше число заканчивается на 13. На 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну. Теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.
Теперь проверим признак для трех: 7+5+1+5+7+6 = 31. Какое ближайшее число разделиться на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576. Конечно, это не единственное решение.
А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.
Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.
Какие задания мы не разобрали и почему
Теперь вы знаете, как сдать базовую математику, решив семь заданий (или больше, конечно!). Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов и методы решения к ним не ограничиваются парой простых алгоритмов.
Например, в эту группу относятся все задания по геометрии: 8, 13, 15, 16. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой.
Задание 17 обычно, хоть и не всегда, содержит неравенство. Это отдельный большой блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет, и попадется задачка на расположение значений на числовой прямой.
Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что семь третьих больше двух, но меньше трех. Корень из 26 равен пяти с копейками, а отрицательная степень сделает из трех пятых пять третьих или чуть больше полутора. Подобные задания надо пытаться делать обязательно!
Задание 20. Здесь попадаются разные типы неочевидных задач на логику. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 20 номере, пишите в комментариях, и Maximum поделится своими методами решения!
Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!