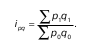что такое базисный индекс
Индивидуальные базисные и цепные индексы. Общие индексы
Для определения статистических индексов нужно иметь данные за два периода или два сравниваемых уровня.
Если существуют данные за определенный ряд периодов или уровней, то в качестве базы для сравнения можно принять один и тот же начальный уровень или уровень предыдущего периода. В первом случае получим индексы с постоянной базой – базисные, а во втором – индексы с переменной базой – цепные.
В экономическом анализе базисные и цепные индексы обладают определенными значениями.
Базисные экономические индексы характеризуют изменение статистических процессов за длительный период времени по отношению к одной отправной точке, но если возникнет необходимость следить за текущими изменениями статистического процесса, то применяются цепные индексы.
Если на основе базисных и цепных индексов исследуется один и тот же период, то это обозначает, что между ними есть взаимосвязь – это произведение цепных индексов, равное базисному. Такая взаимосвязь принесет возможность вычислить базисные индексы по данным цепных индексов, и наоборот.
Общие индексы характеризуют соотношение совокупности статистических процессов или явлений, состоящей из разнородных, непосредственно несоизмеримых элементов. Для определения общей стоимости различных видов продукции в качестве соизмерителя используется обычно цена за единицу продукции, для определения общей себестоимости или производственных затрат – себестоимость единицы продукции, общих затрат труда – затраты труда на производство единицы продукции и т. д.
Общее изменение товарооборота от стоимости проданных товаров можно определять, сопоставив общую стоимость проданных товаров в отчетном периоде по ценам отчетного периода с общей стоимостью проданных товаров в базисном периоде по ценам базисного периода.
Формула общего индекса товарооборота:
Аналогично индексу товарооборота рассчитываются индексы продукции, потребления и т. д.
Приведенная выше формула индекса товарооборота называется агрегатной (от лат. aggrega – «присоединяю»). Агрегатными называются индексы, числители и знаменатели которых представляют собой суммы, произведения или суммы произведений уровней изучаемого статистического явления. Агрегатная формула индекса – основная и наиболее распространенная формула экономических индексов. Агрегатная формула индекса показывает относительное изменение исследуемого экономического процесса и абсолютные размеры этого изменения.
Расчет агрегатного индекса цен был предложен немецким экономистом Г. Пааше.
Что такое базисный индекс
8.5 гЕРОЩЕ Й ВБЪЙУОЩЕ ЙОДЕЛУЩ. йОДЕЛУЩ У РПУФПСООЩНЙ Й РЕТЕНЕООЩНЙ ЧЕУБНЙ
йОДЕЛУЩ НПЗХФ ЙУРПМШЪПЧБФШУС ДМС БОБМЙЪБ ДЙОБНЙЛЙ УПГЙБМШОП-ЬЛПОПНЙЮЕУЛЙИ СЧМЕОЙК ЪБ ОЕЛПФПТЩК ЙОФЕТЧБМ ЧТЕНЕОЙ, ЧЛМАЮБАЭЙК ВПМЕЕ ДЧХИ РЕТЙПДПЧ. ч ЬФПН УМХЮБЕ ТБУУЮЙФЩЧБАФУС УЙУФЕНЩ ЙОДЕЛУПЧ.
ч ЪБЧЙУЙНПУФЙ ПФ ВБЪЩ УТБЧОЕОЙС УЙУФЕНЩ ЙОДЕЛУПЧ ВЩЧБАФ ГЕРОЩНЙ Й ВБЪЙУОЩНЙ.
ьФЙ УЙУФЕНЩ ЙОДЕЛУПЧ НПЗХФ ВЩФШ РПУФТПЕОЩ ДМС ЙОДЙЧЙДХБМШОЩИ Й ПВЭЙИ ЙОДЕЛУПЧ.
уЙУФЕНЩ ЙОДЙЧЙДХБМШОЩИ ЙОДЕЛУПЧ УФПЙНПУФЙ РТПДХЛГЙЙ, ЖЙЪЙЮЕУЛПЗП ПВЯЕНБ РТПДХЛГЙЙ Й ГЕО РТЕДУФБЧМЕОЩ Ч ФБВМЙГЕ 8.5.
оБЪЧБОЙЕ ЙОДЙЧЙДХБМШОПЗП ЙОДЕЛУБ
йОДЕЛУ ЖЙЪЙЮЕУЛПЗП ПВЯЕНБ
бОБМПЗЙЮОП ЬФЙН УЙУФЕНБН ЙОДЕЛУПЧ УФТПСФУС УЙУФЕНЩ ЙОДЙЧЙДХБМШОЩИ ЙОДЕЛУПЧ Й ДМС ДТХЗЙИ РПЛБЪБФЕМЕК.
рТЙ РПУФТПЕОЙЙ УЙУФЕН ПВЭЙИ ЙОДЕЛУПЧ ЙУРПМШЪХАФУС РПУФПСООЩЕ Й РЕТЕНЕООЩЕ ЧЕУБ.
уЙУФЕНПК ЙОДЕЛУПЧ У РПУФПСООЩНЙ ЧЕУБНЙ ОБЪЩЧБЕФУС УЙУФЕНБ УЧПДОЩИ ЙОДЕЛУПЧ ПДОПЗП Й ФПЗП ЦЕ СЧМЕОЙС, ЧЩЮЙУМЕООЩИ У ЧЕУБНЙ, ОЕ НЕОСАЭЙНЙУС РТЙ РЕТЕИПДЕ ПДОПЗП ЙОДЕЛУБ Л ДТХЗПНХ.
оБРТЙНЕТ, УЙУФЕНБ ВБЪЙУОЩИ ЙОДЕЛУПЧ ЖЙЪЙЮЕУЛПЗП ПВЯЕНБ РТПДХЛГЙЙ У РПУФПСООЩНЙ ЧЕУБНЙ (p 0 ) ЙНЕЕФ ЧЙД:
уЙУФЕНХ ГЕРОЩИ ЙОДЕЛУПЧ ЖЙЪЙЮЕУЛПЗП ПВЯЕНБ РТПДХЛГЙЙ У РПУФПСООЩНЙ ЧЕУБНЙ (p 0 ) НПЦОП РТЕДУФБЧЙФШ УМЕДХАЭЙН ПВТБЪПН:
оБРТЙНЕТ, УЙУФЕНБ ВБЪЙУОЩИ ЙОДЕЛУПЧ ГЕО У РЕТЕНЕООЩНЙ ЧЕУБНЙ ЙНЕЕФ УМЕДХАЭЙК ЧЙД:

Б УЙУФЕНБ ГЕРОЩИ ЙОДЕЛУПЧ ГЕО У РЕТЕНЕООЩНЙ ЧЕУБНЙ:
уЙУФЕНЩ ПВЭЙИ ЙОДЕЛУПЧ ДТХЗЙИ РПЛБЪБФЕМЕК УФТПСФУС БОБМПЗЙЮОП. нЕЦДХ ГЕРОЩНЙ Й ВБЪЙУОЩНЙ ЙОДЕЛУБНЙ УХЭЕУФЧХАФ ТБЪМЙЮОЩЕ ЧЙДЩ УЧСЪЙ:
1. еУМЙ ЙЪЧЕУФОЩ ГЕРОЩЕ ЙОДЕЛУЩ, ФП РПУМЕДПЧБФЕМШОП РЕТЕНОПЦЙЧ ЙИ НПЦОП РПМХЮЙФШ ВБЪЙУОЩЕ ЙОДЕЛУЩ.
2. ъОБС РПУМЕДПЧБФЕМШОЩЕ ЪОБЮЕОЙС ВБЪЙУОЩИ ЙОДЕЛУПЧ, НПЦОП ТБУУЮЙФБФШ Б ЙИ ПУОПЧЕ ГЕРОЩЕ ЙОДЕЛУЩ.
Инфляция в моделях. Цепной и базисный индексы
Индекс инфляции в моделях
Долгосрочные финансовые прогнозы охватывают много лет деятельности бизнеса и на протяжении срока планирования цены, использованные в них, будут меняться. Как правило, моделирование основано на текущем значении цен и их ожидаемых изменениях под действием инфляции.
Если планирование основано на номинальных ценах, то все суммы доходов и затрат по статьям, подверженным инфляции, должны меняться от периода к периоду. Если планирование ведется в реальных ценах, то никакие цены не меняются, но прогноз инфляции все равно должен быть представлен в модели, так как эту инфляцию надо будет вычитать из ставки дисконтирования и других аналогичных ставок. Подробнее о номинальных и реальных ценах можно узнать здесь.
Для применения инфляции в модель обычно включают раздел прогноза макроэкономических показателей, который может выглядеть таким образом:
Здесь для применения инфляции к будущим ценам подготовлено два индекса.
Цепной индекс инфляции рассчитывается по отношению к предыдущему периоду. Он как бы по цепочке, от периода к периоду, передает влияние инфляции. Такой индекс удобно использовать по отношению к параметрам, для которых в модели отдельно задана цена и физические объемы.
Базисный индекс инфляции показывает влияние инфляции нарастающим итогом от начала проекта. Он удобен в работе со статьями доходов и затрат, задаваемых денежными суммами, без деления на объемы и цены.
Формула индекса инфляции
Формула расчета индекса инфляции зависит от допущений, принимаемых при построении модели. В приведенном выше примере сделано допущение, что цены в модели были определены в 2021 году, а средние цены 2022 года будут отличаться от них на величину годовой инфляции. Тогда индекс 2022 года равен 1+I22, где I22 — инфляция 2022 года.
Другое возможное допущение — цены были определены в начале 2022 года, равномерно росли с инфляцией в течение года, и среднегодовые цены первого года примерно соответствуют ценам 1 июля — то есть надо считать с влиянием полугодовой инфляции.
Формула первого периода несколько изменится, теперь это:
и вся таблица немного изменит свои значения:
Наконец, мы можем предположить, что цена определена на начало 2022 года, а в модели мы допускаем, что все денежные потоки и цены приходятся на первый день любого расчетного периода. Тогда для первого года никакого влияния инфляции не будет, и таблица примет вид:
Во всех приведенных примерах предполагалось, что шаг планирования финансовой модели — год. Если планирование ведется не по годам, а по кварталам или месяцам, то формула индекса инфляции меняется. Наиболее удобный и универсальный вариант формулы для цепного индекса выглядит так:
где I — годовая инфляция
m — число месяцев в расчетном периоде
Пример реализации индекса инфляции
Подробную инструкцию по включению инфляции в финансовые модели можно посмотреть в этом видео:
Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.
Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.
Цепные и базисные индексы
ИНДЕКСЫ
1.Общее понятие об индексах.
3.Общие (агрегатные) индексы.
4.Цепные и базисные индексы.
1. Общее понятие об индексах.
Индекс – это относительная величина, характеризующая изменение сложных общественных явлений во времени, пространстве или по сравнению с планом.
Индекс = величина сравнения (факт, отчет)
база сравнения (план, базис)
Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана.
Статистика изучает в основном сложные экономические явления, которые состоят из элементов непосредственно несоизмеримых. Так, если электромеханический завод производит несколько видов продукции, то данные о выпуске продукции в натуральном выражении суммировать нельзя. Для того, чтобы показать общее изменение выпуска по нескольким видам продукции и вычисляются индексы. С их помощью можно дать обобщенную характеристику изменения себестоимости, цен, выпуска по нескольким видам продукции.
Индексы позволяют выявить степень изменения изучаемых социально-экономических явлений. С помощью индексов анализируется выполнение планов или нормативов, определяется влияние отдельных факторов на анализируемый показатель и др.
Индексы измеряются в коэффициентах или %-ах.
Индексы бывают индивидуальными и общими (агрегатными).
Для удобства применения индексного метода, составления формул индексов применяются условные обозначения:
i – индивидуальный индекс
I –общий (агрегатный) индекс
pi – цена за единицу продукции
qi – кол-во продукции одного вида в натуральном выражении
zi – себестоимость единицы продукции
Знак внизу справа означает период: 0 – базисный, 1 – отчетный.
2. Индивидуальные индексы.
Индивидуальные индексы –служат для характеристики изменения отдельных элементов сложного явления. Они характеризуют изменение индексируемой величины в текущм периоде по сравнению с базисным, т.е. во сколько раз она возросла или уменьшилась либо сколько % составляет ее рост или снижение. Можно выделить:
| Индивидуальный индекс физического объема | – это отношение количества товара одного вида, проданного в отчетном периоде, к количеству того же товара, проданного в базисном периоде. |
Поскольку базисный уровень индексируемого показателя приравнивается к 1 или 100%, то разность между полученным индексом и 1 или 100% характеризует относительную величину изменения количества проданного товара. По этому индексу можно определить и абсолютное изменение количества проданного товара в натуральном выражении как разность между числителем и знаменателем индекса.
| Индивидуальный индекс цен | – это отношение цены отдельного товара в отчетном периоде к цене его в базисном периоде. |
Разность между числителем и знаменателем его покажет абсолютное изменение цены за единицу товара в рублях.
| Индивидуальный индекс товарооборота (стоимости) | характеризует изменение товарооборота по одному товару и строится как отношение товарооборота отчетного периода к товарообороту базисного периода |
Разница между числителем и знаменателем его покажет абсолютное изменение товарооборота в рублях за счет двух факторов: изменения количества проданного товара и изменения цены этого товара.
Индивидуальные индексы взаимосвязаны между собой: индекс товарооборота равен произведению индекса физического объема на индекс цен, то есть
| Индивидуальный индекс себестоимости продукции | – это отношение себестоимости отдельного товара в отчетном периоде к его себестоимости в базисном периоде. |
Разница между числителем и знаменателем его покажет абсолютное изменение себестоимости единицы продукции в рублях.
3. Общие (агрегатные) индексы.
Общие индексы используются для сопоставления непосредственно несоизмеримых, разнородных явлений; они характеризуют изменение не отдельного элемента сложного явления, а всего явления в целом.
Например, с помощью общих индексов можно охарактеризовать динамику объемов всей выпускаемой продукции на мебельной фабрике, изготавливающей различные виды продукции: столы, стулья, диваны, шкафы. Однако нельзя просто сложить объемы продукции различных видов за два периода. Такое суммирование бессмысленно не только из-за различных единиц измерения (тонны, штуки, метры), но и из-за того, что каждый продукт имеет свое назначение и произведен с разными затратами средств и времени.
Чтобы сделать сопоставимыми несоизмеримые элементы, нужно выразить их общей мерой: стоимостью, трудовыми затратами и т.п. Эта задача решается построением и расчетом общих индексов.
Основной формой общих индексов являются агрегатные индексы.
Агрегатный индекс характеризует общее изменение объема производства, объема продаж, уровней цен и т.д. в целом по всей совокупности. Выделяют:
| Агрегатный индекс физического объема | — это отношение условной стоимости произведенных в текущем периоде товаров в ценах базисного периода к фактической стоимости товаров, произведенных в базисном периоде; |
| — характеризует, как изменился в среднем общий объем продукции. |

В основном при построении агрегатного индекса физического объема продукции в качестве соизмерителей применяются сопоставимые, неизменные, фиксированные цены на уровне базисного периода, что позволяет устранить влияние изменения цен на динамику количества продукции.
Абсолютное изменение физического объема:
| Агрегатный индекс цен | — изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде; |
| — характеризует, как изменились в среднем цены на различные виды продукции (фактическую экономию или перерасход). |
Абсолютное изменение цен:
| Агрегатный индекс стоимости продукции | — это отношение стоимости продукции текущего периода к стоимости базисного периода; |
| — характеризует изменение фактической стоимости произведенной или реализованной продукции. |
Абсолютное изменение стоимости в отчетном периоде по сравнению с базисным одновременно за счет изменения физического объема продаж и изменения цен:
Взаимосвязь индексов можно представить в виде:
4. Цепные и базисные индексы.
Если при исчислении индексов сравниваемых периодов три и более, то возникает вопрос о выборе базы сравнения. В зависимости от базы сравнения различают:
Выбор системы индексов определяется задачами анализа. Для оценки скорости происходящих изменений от периода к периоду используют цепные индексы. Если же необходимо определить общие изменения экономического явления за конкретный исторический период, рассчитывают базисные индексы.
Цепные и базисные индексы могут быть как индивидуальные, так и общие.
Базисные индивидуальные индексы физического объема:



Цепные индивидуальные индексы физического объема:



Базисный агрегатный индекс физического объема продукции:


Цепной агрегатный индекс физического объема продукции:


ИНДЕКС БАЗИСНЫЙ
Пункт отсчета, по к-рому измеряется скорость изменения цифровых показателей по за-кладной с переменной ставкой процента. Уровень И.б. известен при оформлении закладной; определяемая с недавних пор величина серии цифровых показателей на дату закрытия ссуды или на период в шесть месяцев до нее. В целом максимальное изменение ставки с момента выдачи закладной с переменной ставкой не может превысить разницу между текущей величиной индекса и величиной И.б
Смотреть что такое «ИНДЕКС БАЗИСНЫЙ» в других словарях:
Индекс цен базисный — базисный индекс рассчитывается как отношение цены текущего периода к цене периода, принятого за базу. Источник: Постановление Госкомстата РФ от 25.03.2002 N 23 Об утверждении Основных положений о порядке наблюдения за потребительскими ценами и… … Официальная терминология
Базисный процентный своп — своп процентных ставок, при котором один индекс с плавающей ставкой обменивается на другой индекс с плавающей ставкой в одной валюте. По английски: Basis rate swap См. также: Свопы процентных ставок Финансовый словарь Финам … Финансовый словарь
Индекс Ласпейреса — один из видов индексов цен, характеризующих изменения цен товаров. Рассчитывается по так называемой формуле или схеме Ласпейреса. Последняя применяется также для построения общего индекса цен (дефлятора), индекса физического объема товарооборота … Словарь бизнес-терминов
индекс цен базисный — Рассчитывается как отношение цены текущего периода к цене периода, принятого за базу сравнения. В статистический практике стран со стабильной экономикой Б.и.ц. традиционно отдается предпочтение. При этом в качестве основных его достоинств… … Справочник технического переводчика
Индекс (информационные технологии) — У этого термина существуют и другие значения, см. Индекс. В информатике индекс может быть: Целое число, которое идентифицирует элемент массива Структура данных с сублинейным временем поиска Содержание 1 Идентификатор элемента массива … Википедия
Индекс (массив) — У этого термина существуют и другие значения, см. Индекс. Индекс в языках программирования элемент перечислимого множества, который указывает на конкретный элемент массива, обычно является неотрицательным скалярным целым числом. Есть три… … Википедия
Базисный год — BASE YEAR Год, принимающийся за базу при расчете индексов. Например, базисным годом текущего индекса розничных цен в Великобритании является 1987 год, т.е. индекс этого года принимается за 100. В 2002 г. индекс цен равнялся 173. Это означает, что … Словарь-справочник по экономике
БАЗИСНЫЙ ГОД — – исходный период, относительно которого производится индексация. Например, в Великобритании в качестве базисного выбран 1987. Это значит, что средняя цена типичной продовольственной корзины в 1987 выбрана базой индекса и равна 100. В 1992 цены… … Экономика от А до Я: Тематический справочник