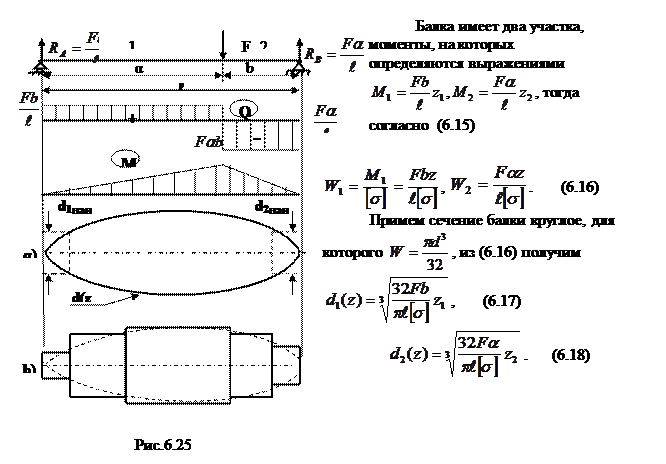что такое балка равного сопротивления

Балки переменного сечения и балки равного сопротивления

По конструктивным или иным причинам часто приходится выполнять балку с пере-менным сечением.

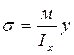
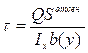
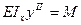
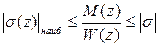
Формулы, , ,полученные для балок с постоянным сечением на основании гипотезы плоских сечений, становятся неверными (как и сама гипот-еза). Однако, методами теории упругости показано, что если угол наклона образующей повер-хности стержня к его оси не превышает 15-20 градусов, то с достаточной для практики точ-ностью можно пользоваться обычным условием прочности . Формула Журавского в этом случае дает значительные погрешности.

Частным случаем балок с непрерывно изменяющимися размерами сечения по её длине являются балки равного сопротивления изгибу.

Балкой равного сопротивления называется балка, у которой во всех сечениях максимальное напряжение равно допускаемому: .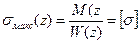

Отсюда получается уравнение для определения размеров балки равного сопротивления:

(6.15)

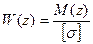
Задавшись какой-либо формой сечения, размеры которого будут определяться только одним параметром, из уравнения (6.15) можно определить закон изменения этого параметра по длине балки.

Найдём закон изменения поперечного сечения балки равного сопротивления, изображённой на рис.6.25

Возле опор напряжения в балке малы, а потому размеры сечения будут определяться касательными напряжениями: 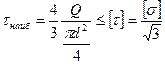. (6.19)

Подставляя в (6.17) значения Q для каждого участка, получим значения диаметров балки на её концах (6.25 α): ,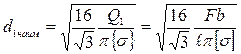

.

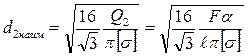
Переход к балке равного сопротивления позволяет уменьшить её массу и увеличить податливость, т.е., при тех же силах увеличатся её прогибы, что ей позволяет воспринимать безопасно большие энергии. Поэтому балка равного сопротивления лучше сопротивляется ударным нагрузкам.

Согласно (6.17), (6.18) рассмотренная балка будет иметь параболические очертания. Изготовление такой балки связано с большими технологическим трудностями, поэтому на практике применяют не балки равного сопротивления, а близкие к ним ступенчатые балки

Примером балки равного сопротивления может служить автомобильная рессора, масса которой в два раза меньше, а податливость в 1,2-1,4 раза больше в сравнении с балкой постоянного сечения.

Источник

Расчет балок равного сопротивления изгибающему моменту

Теоретические предпосылки и допущения, принимаемые при расчете балок переменного сечения

1. Расчет допускается выполнять на основе теоретических предпосылок и допущений, принимаемых при формулировке задач теории сопротивления материалов.

2. Так как значения изгибающих моментов, продольных и поперечных сил не зависят от геометрических характеристик рассматриваемого сечения, то эти значения при расчетах балок переменного сечения принимаются такими же, как и для балок постоянного сечения.

3. В качестве балок переменного сечения могут рассматриваться только такие тела, изменение геометрических параметров сечения которых не влияет на положение нейтральной оси, или соотношение длины балки к изменению высоты по длине больше 50: l/Δh ≥ 50, так как в этом случае влияние горизонтальных опорных реакций, возникающих из-за непрямолинейности нейтральной оси балки, можно не учитывать.

4. При изменении ширины сечения по длине следует учитывать особенности приложения нагрузки. Для элементов конструкции, к которым приложена сосредоточенная нагрузка в месте наибольшей ширины, следует учитывать местную концентрацию напряжений в месте приложения сосредоточенной нагрузки. Если 50 > l/Δh > 10, то такой элемент можно рассматривать как стержень переменного сечения малой кривизны (большого радиуса кривизны). При l/Δh 2 /6 (320.1.2.2)

При несимметричных нагрузках, при несимметрично изменяющихся параметрах сечения, при непрямоугольных поперечных сечениях и при расчете многопролетных статически неопределимых балок следует использовать методы дифференциального исчисления, позволяющие учесть указанные особенности.

Если изменения геометрических параметров и действующие нагрузки симметричны относительно оси проходящей через середину пролета, то для балок прямоугольного сечения сделать это можно следующим образом:

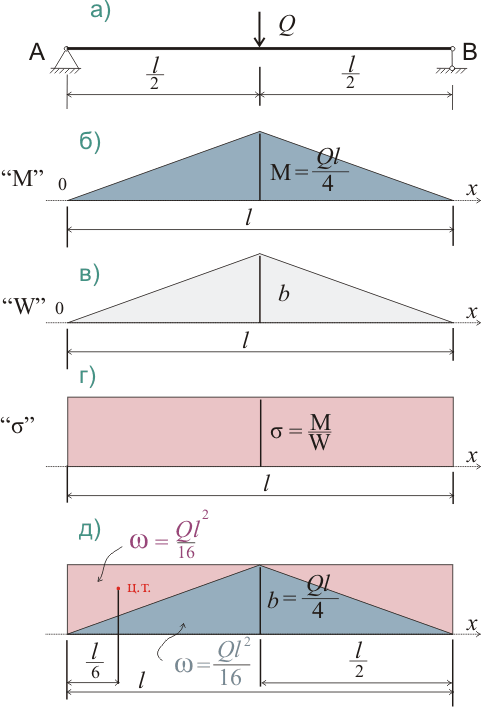
8. 1. Если эпюра изменения одного из параметров описывается той же зависимостью, что и эпюра моментов, то такую балку можно рассматривать, как балку пропорционального сопротивления, а если при выбранных параметрах сечения напряжения остаются постоянными, то такая балка называется балкой равного сопротивления изгибающему моменту. Балка, изменение ширины которой показано на рис. 320.1.в), при приложении сосредоточенной нагрузки посредине балки (рис. 320.1.а) будет балкой равного сопротивления изгибающему моменту. При этом эпюра моментов будет обычной, а эпюра нормальных напряжений для такой балки также будет иметь вид прямоугольника (рис. 320.3.г):

Рисунок 320.1

8.2. Если эпюру моментов наложить на эпюру нормальных напряжений, то разница эпюр покажет изменение прогиба балки.

Для того, чтобы корректно наложить эпюры, воспользуемся следующим допущением. Если значение напряжений в середине пролета рассматривать как некое единичное (σ_l/2 = 1) и при постоянной высоте сечения h значение h 2 /6 заменить постоянной С, также равной единице (С = 1), то тогда согласно формул (320.1.1) и (320.2.2):

1 = М/bC = М/b (320.3.1)

b = M = Ql/4 (320.3.2)

8.3. Прогиб балки постоянного сечения можно определить по эпюре моментов и напряжений графо-аналитическим методом.

Вкратце суть графоаналитического метода состоит в том, что эпюра изгибающего момента рассматривается как некая фиктивная нагрузка. Соответственно, чтобы определить фиктивную опорную реакцию от такой нагрузки, нужно определить площадь эпюры (это будет угол поворота на опоре А), а чтобы определить значение фиктивного изгибающего момента, нужно сначала умножить значение фиктивной опорной реакции на расстояние до рассматриваемой точки и затем вычесть из этого значения площадь эпюры фиктивной нагрузки, умноженную на расстояние от центра тяжести фиктивной нагрузки до рассматриваемой точки (это будет прогиб посредине пролета).

8.4. Тогда если площадь фигуры, показывающей разницу между эпюрой моментов и эпюрой напряжений, умножить на расстояние от центра тяжести этой фигуры до середины пролета, то полученный фиктивный момент будет показывать разницу между прогибом балки постоянного сечения и прогибом балки изменяющегося сечения при той же нагрузке.

Для балки, показанной на рисунке 320.1 дополнительный прогиб, вызванный равномерным распределением напряжений по всей длине балки, составит:

В данной случае I_b означает, что мы рассматриваем изменение прогиба по отношению к балке с постоянным моментом инерции и соответственно постоянной шириной сечения b.

Общий прогиб балки равного сопротивления изгибающему моменту составит:

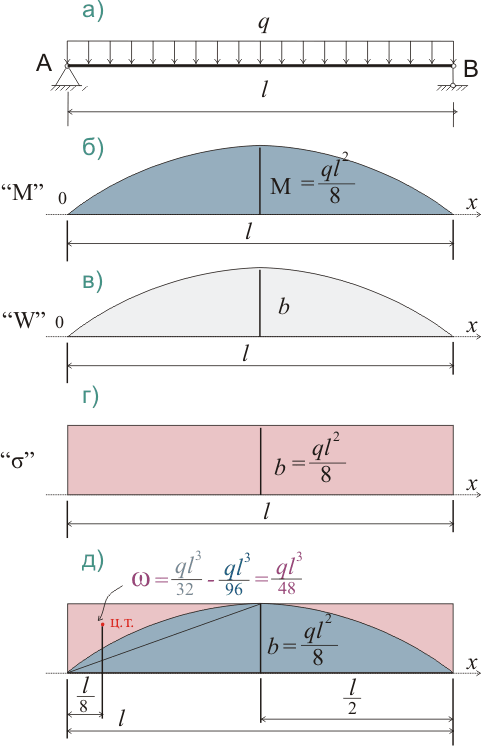
Балка равного сопротивления изгибающему моменту при действии равномерно распределенной нагрузки по всей длине балки будет иметь другие параметры поперечного сечения, однако принцип расчета остается таким же:

Рисунок 320.2

Для балки с равномерно распределенной нагрузкой:

Тогда прогиб балки равного сопротивления изгибающему моменту составит:

f_об = f_п + f_σ = 5ql 4 /384EI_b + ql 4 /384EI_b = ql 4 /64EI_b (320.5.2)

А если балка имеет не равное сопротивление изгибающему моменту, например, ширина сечения балки изменяется линейно (рис.320.1.в), то следует учесть дополнительный прогиб, возникающий из-за неравномерного распределения напряжений:

M σ _ф = ql 3 /96(l/4) = ql 3 /384; f σ = ql 4 /384EI_b (320.5.3)

Тогда общий прогиб балки не равного сопротивления изгибающему моменту составит:

f_об = f_п + f_σ + f σ = 5ql 4 /384EI_b + ql 4 /384EI_b + ql4/384EI_b = 7ql 4 /384EI_b (320.5.4)

Примечание: Принципы определения площадей фигур, описанных различными кривыми и определения центра тяжести таких фигур в данной статье не рассматриваются.

9. Расчет балок равного сопротивления изгибающему моменту с изменяющейся высотой отличается только тем, что согласно формулы (320.1.2.2) высота сечения будет выражаться квадратным корнем из изгибающего момента.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Благодарю Вас за такой труд. Нигде так понятно не описываются темы строймеха, как здесь. Помогло мне разобраться в очень многих вещах)
Хотелось бы больше примеров расчетов, конечно, а не только общих формул.

Прошу помогите с расчётом, пожалуйста. Взяла у вас талончик, жду ответа

Ольга, я отправил вам письмо.

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

Балки равного сопротивления

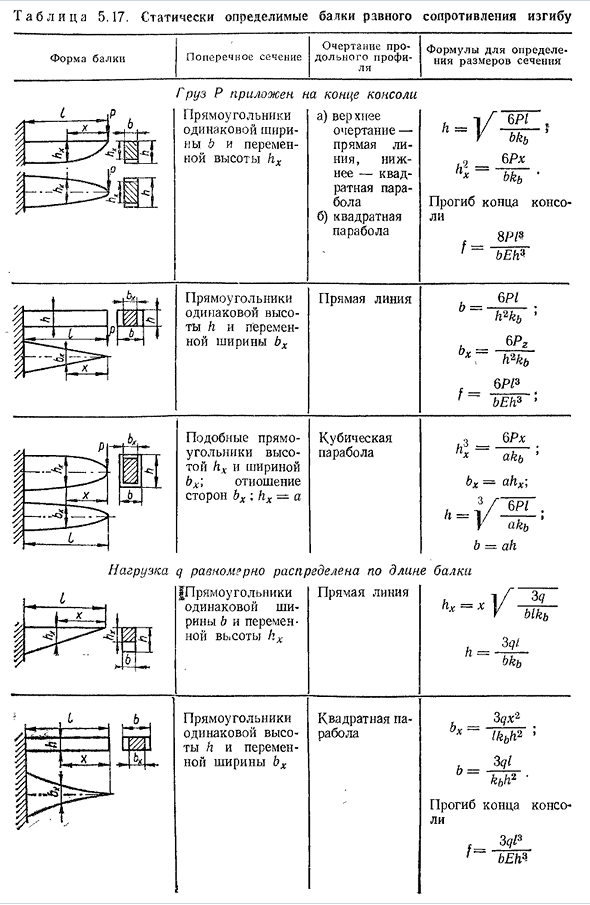
Балки равного сопротивления

Балка равного сопротивления Форма балки с равным сопротивлением определяется из условия, что во всех сечениях напряжение такое же, как и заданное. stmax — — — = const где M и G обозначают максимальный изгибающий момент в сечении

сопротивления G o-момент L4max, тогда G#= 143T а б л и Ц А5. 17. Статически определяемые балки с равным сопротивлением изгибу Форма поперечного сечения балки форма продольного

профиля Выражение для определения размера сечения Груз Р крепится Людмила Фирмаль

к консоли прямоугольной кромкой одинаковой ширины b и переменной высоты hx а) верхний контур-прямая линия, а нижний-парабола квадрата б)парабола квадрата,, 6px h*

BKT■отклонение консольного конца beh3 Прямоугольник

с одинаковой высотой h и переменной шириной BX Прямой 6P1 QP13 bEh3′ Аналогичная прямоугольная высота hx и ширина BX; соотношение сторон bx; hx=a Л Кубическая парабола Ресивер BRX АКБ ’ ВХ = ahx по; Б=а Нагрузка q равномерно распределяется

форма продольного профиля Выражение для определения размера сечения Высота HX и ширина bx аналогичны прямоугольнику; аспект BX: hx==a Полукубические параболы Zdx2ak/, 1’bx-ahx по, Б=а Равная ширина b и переменная высота HX, L прямоугольник Контур выше представляет собой эллипс ’•=] / Сайт 3D1 4bkh

самое большое отклонение 3qP16X13 — ^м топор ■ м. Любой момент сопротивления Г Людмила Фирмаль

(H)= раздел x доступен для записи: М-Макс (5.43)) — Размеры детали, где изгибающий момент близок к нулю, выбираются из условий прочности тангенциального напряжения. В таблице приведена формула для определения размеров поперечного сечения нескольких типов статически определяемых балок одинакового сопротивления. 5.17

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Балки равного сопротивления изгибу

Лекция №17

Тема: «Изгиб»

Рациональные формы сечения балок

Балки равного сопротивления изгибу

Рациональные формы сечения балок

Таким образом, рациональны те формы поперечного сечения, у которых основная часть площади удалена как можно дальше от нейтральной линии. Этому в первую очередь удовлетворяют балки двутаврового сечения, у них основная часть материала сконцентрирована в удаленных от нейтрального слоя полках (см. рис. 1).

Менее выгодно прямоугольное сечение, особенно вытянутое вдоль нейтральной оси (W_y > W_x). Не выгодно круговое сечение, так как оно имеет наибольшую толщину на уровне нейтрального слоя (см. рис. 2), где материал не загружен, т.е. не работает.

Полое сечение (трубчатое, коробчатое и др.) всегда выгоднее сплошного, равноценного по площади, а, следовательно, и по массе.

Основным балочным прокатным профилем является двутавр. Различают двутавры обыкновенные и широкополочные. Первые применяют давно и пока они в строительстве более распространены. Они имеют уклон внутренних граней полок. Широкополочные двутавры начали прокатывать в конце 70-х годов. Они имеют параллельные грани полок, что облегчает крепление примыкающих деталей, и более экономичны.

Рис. 1 Рис. 2

Для хрупких материалов симметричный профиль относительно нейтральной оси нерационален. Целесообразно, чтобы высота сжатой зоны была больше растянутой, так как прочность хрупких материалов на сжатие выше, чем на растяжение (см. рис. 3).

Рис. 3

Балки равного сопротивления изгибу

В большинстве случаев изгибающий момент М изменяет свою величину по длине балки. Поэтому, если балку выбрать постоянного сечения, то на участках, где изгибающий момент меньше максимального, она будет недогружена. С точки зрения рационального расхода материала балка должна иметь переменное сечение в зависимости от М с таким расчетом, чтобы в каждом сечении:

(1)

Такие балки называют балками равного сопротивления изгибу.

Рассмотрим пример. Для балки равного сопротивления изгибу, имеющую круглое сечение, определить диаметр (рис. 4).

Решение: Поскольку задача симметрична, то реакции опор одинаковы и равны , а эпюра изгибающих моментов будет симметрична.

Изгибающий момент в произвольном сечении будет равен:

Из формулы (1) получим:

.

Для круглого сечения:

.

(2)

Уравнение (2) представляет собой параболу 3-го порядка. Строим эпюру диаметра d (см. рис. 4). Поскольку изготовить балку (ось) такого сложного профиля трудно, ее изготавливают ступенчатой, причем необходимым условием является то, чтобы диаметр не был меньше диаметра, полученного по формуле (2).

Источник

Что такое балка равного сопротивления

Подбор сечений балок равного сопротивления.

Все предыдущие расчеты относились к балкам постоянного сечения. На практике мы имеем часто дело с балками, поперечные размеры которых меняются по длине либо постепенно, либо резко.

Ниже рассмотрено несколько примеров подбора сечения и определения деформаций балок переменного профиля.

Так как изгибающие моменты обычно меняются по длине балки то, подбирая ее сечение по наибольшему изгибающему моменту, мы получаем излишний запас материала во всех сечениях балки, кроме того, которому соответствует . Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления. Под этим названием подразумевают балки, у которых во всех сечениях наибольшее нормальное напряжение одинаково и должно быть равно допускаемому.

Условие, определяющее форму такой балки, имеет вид

Здесь М(х) и W(x) — изгибающий момент и момент сопротивления в любом сечении балки; W(х) для каждого сечения балки должен меняться пропорционально изгибающему моменту.

Эти условия справедливы и для сечения с наибольшим изгибающим моментом; если обозначить — момент сопротивления балки в сечении с наибольшим изгибающим моментом , то можно написать:

Покажем ход вычислений на примере. Рассмотрим балку пролетом l, защемленную концом А и нагруженную на другом конце силой Р (Рис.1). Выберем сечение этой балки в виде прямоугольника; задачу о надлежащем изменении момента сопротивления можно решать, меняя высоту или ширину балки или тот и другой размер вместе.

Рис.1. Расчетная схема балки равного сопротивления

Пусть высота балки будет постоянной , а ширина переменной—. Момент сопротивления в сечении на расстоянии х от свободного конца будет , а изгибающий момент ; момент сопротивления опорного сечения , a наибольший изгибающий момент в опорном сечении . В расчете имеют значения лишь абсолютные величины М(х) и

По формуле (1) получаем:

т. е. ширина меняется по линейному закону в зависимости от х. При ширина равна .

Вид балки в фасаде и плане показан на Рис.1. Такое очертание балки получается, если учитывать ее прочность только по отношению к нормальным напряжениям; ширина в сечении В обращается в нуль.

Однако необходимо обеспечить прочность и по отношению к касательным напряжениям. Наименьшая ширина балки, требуемая этим условием, определится из уравнения

или, так как

Таким образом, исправленное очертание балки предопределяет минимальный размер ширины и утолщение свободного края консоли.

Определение деформаций балок переменного сечения.

При определении прогибов и углов поворота для балок с переменным сечением надлежит иметь в виду, что жесткость такой балки является функцией от х. Поэтому дифференциальное уравнение изогнутой оси принимает вид

где J(x) — переменный момент инерции сечений балки.

До интегрирования этого уравнения можно выразить J(x) надлежащей подстановкой через J, т. е. через момент инерции того; сечения, где действует ; после этого вычисления производятся так же, как и.для балок постоянного сечения.

Покажем это на примере, разобранном выше. Определим прогиб балки равного сопротивления, защемленной одним концом, нагруженной на другом конце силой Р и имеющей постоянную высоту. Начало координат выберем на свободном конце балки.

Дифференциальное уравнение принимает вид:

Интегрируем два раза:

Для определения постоянных интегрирования имеем условия: точке А при прогиб и угол поворота или

и

и

Выражения для у и принимают вид;

Наибольший прогиб на свободном конце балки В получится при : он равен

Если бы мы всю балку сделали постоянного сечения с моментом инерции J, то наибольший прогиб был бы

т. е. в 1 раза меньше.

Таким образом, балки переменного сечения обладают большей гибкостью по сравнению с балками постоянной жесткости при одинаковой с ними прочности. Именно поэтому, а не только ради экономии материала, они и применяются в таких конструкциях, как рессоры.

Источник