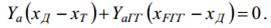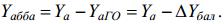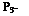что такое балансировка самолета

Основные понятия и определения

БАЛАНСИРОВКА САМОЛЕТА

На самолетах вертикального взлета и посадки балансировка осуществляется и на режиме висения-с помощью струйных (газодинамических) рулей.

На вертолете она обеспечивается изменением направления и силы тяги несущего (несущих) и рулевого винтов, а также отклонением стабилизатора, руля направления (где они имеются).

УСТОЙЧИВОСТЬ И УПРАВЛЯЕМОСТЬ САМОЛЕТА

Основные понятия и определения

При рассмотрении траекторных задач динамики полета обычно полагают, что все силы, действующие на самолет, приложены в его центре масс.

Рис.1.7.1. Схема сил, действующих на самолет как на материальную точку.

Это упрощает рассуждения и расчет основных параметров полета, но не позволяет определить все условия, которые необходимо обеспечить для выполнения заданного режима полета. Например, для горизонтального полета с заданной скоростью необходим определенный угол атаки. Какое для этого требуется отклонение руля высоты и хватит ли максимального отклонения руля для балансировки самолета на заданном угле атаки? Для ответа на этот вопрос необходимо рассмотреть моменты сил, действующих на самолет, и возникающее в результате их воздействия вращательное движение самолета. Для определения моментов необходимо знать, как известно из механики, величину каждой силы и точку ее приложения, а также оси координат, относительно которых определяются моменты сил.

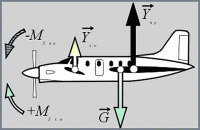
Обычно моменты определяются относительно осей, проходящих через центр масс самолета. Это позволяет исключить из рассмотрения момент, создаваемый силой тяжести mg, приложенной в центре масс. Поэтому, в дальнейшем на схемах для определения моментов сила тяжести изображаться не будет, а центр масс будет показан как шарнир, относительно которого происходит вращение самолета.

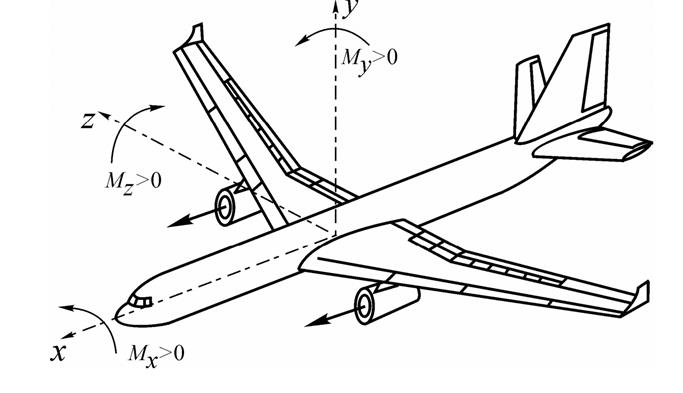
Моменты, действующие на самолет, обычно рассматриваются в связанной системе координат oxyz, начало координат которой располагается в центре масс самолета, а оси координат направлены следующим образом:

Рис.1.7.2. Аэродинамические моменты, действующие на самолет
относительно осей связанной системы координат.

Составляющие моментов, действующих на самолет, в связанной системе координат имеют следующие названия:

Эти названия были принесены в авиацию сто лет назад в основном из французского языка. Так «тангаж» у французских моряков означает килевую качку корабля, «кабре» означает у кавалеристов «встать на дыбы». По этим терминам можно представить из кого формировались ряды первых авиаторов и с чем они сравнивали свои, видимо не очень послушные воле пилотов, аэропланы.

Величины аэродинамических моментов рассчитываются по формулам, аналогичным формулам для аэродинамических сил:

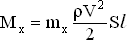	(1.7.1)
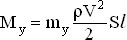	(1.7.2)
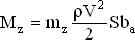	(1.7.3)

где:
, , – коэффициенты моментов крена, рысканья и тангажа соответственно;
S – площадь крыла;
– размах крыла;
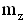
– средняя аэродинамическая хорда крыла.

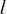
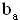
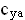
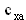
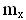
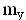
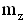
Как и коэффициенты подъемной силы и лобового сопротивления , величины , , зависят от геометрических характеристик самолета, его конфигурации и отклонения рулей, а также углов атаки и скольжения и критериев аэродинамического подобия. Кроме того, как видно из формул, величины аэродинамических моментов зависят от плотности воздуха, скорости полета, площади и характерного геометрического размера крыла. Необходимо отметить, что если для моментов крена и рысканья в качестве характерного геометрического размера выбирается размах крыла, то для момента тангажа используется средняя аэродинамическая хорда, определение которой будет дано в п.1.7.2.

Коэффициенты моментов в отличии от самих моментов являются величинами безразмерными и не зависят от плотности воздуха, скорости полета, площади и геометрических размеров крыла. Поэтому удобнее в расчетах использовать коэффициенты моментов, а величины моментов по ним всегда можно определить по формулам (1.7.1-1.7.3).

Причиной возникновения моментов крена и рысканья является несимметричное обтекание самолета, возникающее при полете со скольжением, либо при отклонении элеронов или руля направления. В этом случае возникает так называемое боковое движениесамолета. В случае симметричного обтекания на самолет действует только момент тангажа. Движение самолета в этом случае происходит в плоскости симметрии самолета и называется продольным. Основными параметрами продольного движения является скорость и угол атаки. Для управления самолетом по тангажу используется руль высоты(РВ).

В диапазоне летных углов атаки, когда сохраняется безотрывное обтекание крыла продольное и боковое движение самолета можно рассматривать независимо друг от друга. При больших углах атаки такой подход недопустим из-за их взаимного влияния. Например, при увеличении угла атаки до критического происходит обычно сваливание самолета на крыло, т.е. изменение параметра продольного движения – угла атаки приводит к возникновению бокового движения крена.

По этой причине, рассматривая отдельно продольное и боковое движение, необходимо помнить, что все эти рассуждения справедливы только в диапазоне летных углов атаки.

Движение самолета с учетом его вращения изучается в разделе динамики полета «Устойчивость и управляемость самолета». В этом разделе используются следующие основные понятия:

В полете самолет находится под постоянным воздействием различных возмущений, связанных с перемещением воздушных масс в атмосфере. Эти возмущения стремятся вывести самолет из равновесия и изменить режим полета. В таких условиях благодаря устойчивости упрощается пилотирование самолета, т.к. самолет сохраняет заданный режим полета и парирует возникающие возмущения самостоятельно. Выдающийся русский аэродинамик Н.Е. Жуковский в одной из своих научных работ назвал это качество «прочностью движения». Пилоты, чтобы отметить высокую устойчивость самолета, говорят, что «самолет плотно сидит в воздухе».

Для количественной оценки устойчивости используются различные критерии устойчивости, которые определяют реакцию самолета или характер переходного процесса при воздействии на самолет внешнего возмущения.

Для упрощения рассуждений устойчивость самолета условно делят на динамическуюи статическую. Рассмотрим различие между статической и динамической устойчивостью на примере реакции самолета на воздействие вертикального восходящего порыва ветра, за счет которого происходит увеличение угла атаки. Т.к. рассматривается устойчивость самолета, то пилот не вмешивается в управление, и самолет должен «самостоятельно» вернуться к первоначальному углу атаки после прекращения действия порыва ветра. Очевидно, что для этого необходимо при увеличении угла атаки возникновение пикирующего момента, стремящегося уменьшить угол атаки. Такой момент называется стабилизирующим. Он всегда направлен на возврат самолета к первоначальному режиму полета. А способность самолета создавать стабилизирующие моменты и называется статической устойчивостью.

Однако возникновение стабилизирующего момента не всегда приведет к возврату самолета на первоначальный угол атаки. Например, при излишне большом значении стабилизирующего момента возможно возникновение незатухающих колебаний относительно исходного угла атаки. В этом случае говорят, что самолет, обладая статической устойчивостью, динамически неустойчив. Таким образом, статическая устойчивость является необходимым, но недостаточным условием динамической устойчивости, которую можно рассматривать как полную устойчивость в соответствии с приведенным выше определением.

Для статически неустойчивого самолета при увеличении угла атаки возникает дестабилизирующийкабрирующий момент, под действием которого происходит дальнейшее увеличение угла атаки, и возврат к первоначальному углу атаки без вмешательства пилота будет невозможен. Поэтому в этом случае можно сразу сделать вывод, что самолет не обладает статической, а, следовательно, и динамической устойчивостью.

Рис.1.7.3. К объяснению понятий статическая и динамическая устойчивость самолета.

В данном разделе будут рассмотрены продольная балансировка, а также продольная статическая устойчивость и продольная статическая управляемость самолета.

Источник

БАЛАНСИРОВКА, УСТОЙЧИВОСТЬ, УПРАВЛЯЕМОСТЬ

Небольшие не связанные с управлением заранее неизвестные отклонения (возмущения) аэродинамической силы и силы тяги от расчетных значений, также изменяют движение самолета. Для выполнения полета самолет должен противостоять этим возмущениям, т.е. быть устойчивым.

Устойчивость и управляемость являются важными свойствами самолета, определяющими возможность и безопасность полета, требуемые усилия пилота и автоматических устройств при управлении, уровень комфорта экипажа и пассажиров в полете.

При исследовании устойчивости и управляемости самолет рассматривается как материальное тело и его движение описывается уравнениями движения центра масс и вращения вокруг центра масс.

Движение центра масс самолета и его вращение относительно центра масс связаны. Однако совместное изучение этих движений весьма затруднительно ввиду большого числа уравнений, описывающих общее движение самолета.

В реальном движении как правило выполняются следующие условия:

во-первых, отклонение органов управления практически мгновенно приводит к изменению аэродинамических сил, действующих на самолет,

во-вторых, возникающие при этом управляющие силы существенно меньше основных аэродинамических сил.

Эти условия позволяют считать, что угловое движение самолета, в отличие от движения его центра масс, можно изменить достаточно быстро и, следовательно, движение (вращение) самолета относительно центра масс и движение центра масс по траектории можно рассматривать отдельно.

Для осуществления равномерного и прямолинейного движения необходимо, чтобы сумма сил и моментов, действующих на самолет, равнялась нулю. В этом случае самолет находится в равновесии. Примерами такого движения являются горизонтальный полет, снижение, набор высоты.

В случае если равна нулю только сумма моментов, действующих на ЛА, такое состояние называется балансировкой. Например, при установившемся развороте (разворот с постоянной скоростью) сумма сил, действующих на ЛА, не равна нулю, а сумма моментов этих сил равна нулю. Следовательно, в этом виде полета самолет находится только в состоянии балансировки.

В реальном полете самолет, конечно же, не находится в состоянии равновесия. Причиной этого является турбулентность атмосферы, то есть наличие постоянных порывов ветра различной интенсивности и направления. Эти ветровые воздействия, изменяя угол атаки, скорость ЛА, перегрузку и другие параметры полета, изменяют величину и точку приложения равнодействующей аэродинамической силы, то есть выводят ЛА из состояния равновесия.

Все самолеты гражданской авиации обладают свойством восстанавливать нарушенное в полете равновесие (это свойство заложено в самолете конструктивно). Это значительно облегчает их пилотирование и повышает безопасность полета. Способность самолета самостоятельно (без вмешательства летчика) сохранять и восстанавливать нарушенное по причине внешнего воздействия равновесие называется устойчивостью.

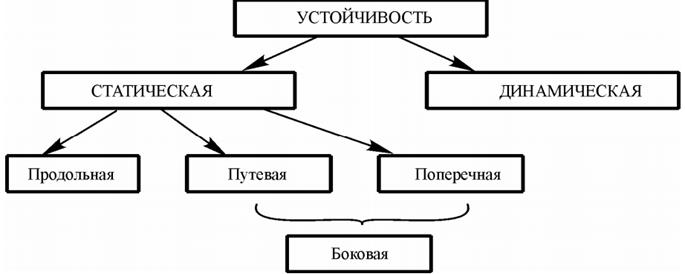
Понятие «устойчивость» включает в себя несколько составляющих, что можно представить в виде схемы.

Рисунок 13- Устойчивость ВС

Способность самолета создавать моменты, стремящиеся вернуть ЛА в заданное положение равновесия, называется статической устойчивостью.

Самолет считается статически устойчивым, если при нарушении равновесия возникают такие силы и моменты, которые стремятся вернуть его в прежнее состояние.

Самолет считается статически неустойчивым, если при нарушении равновесия возникающие силы и моменты стремятся увести его еще дальше от положения равновесия. Если же при нарушении равновесия никакие моменты не возникают, то такой ЛА называется статически нейтральным. Как уже было сказано, эти моменты возникают (либо не возникают) без вмешательства летчика.

Статическая устойчивость является необходимым условием динамической устойчивости. Динамическая устойчивость изучает поведение самолета под воздействием сил и моментов, возникающих в процессе возмущенного движения. Признаком динамической устойчивости является затухающий характер колебаний самолета относительно положения равновесия при возвращении его к исходным параметрам после окончания действия возмущающего фактора. Эти колебания носят затухающий характер из-за возникновения демпфирующих моментов, появляющихся в результате вращения ЛА вокруг центра масс.

Рисунок 14- Самолет в связанной системе координат.

В процессе полета всегда возникает необходимость изменения положения ЛА в пространстве, что становится возможным благодаря свойству управляемости ЛА.

Управляемость – это способность ЛА переходить из одного невозмущенного движения к другому при воздействии на органы управления ЛА. (Управляемость не следует путать с маневренностью. Управляемость характеризуется перемещением ЛА вокруг его центра масс (ц.м.), а маневренность – перемещением ц.м. в пространстве.)

Равновесие, устойчивость и управляемость рассматриваются относительно осей связанной системы координат (рис. 4).

Одним из свойств самолета, обеспечивающих полет, является его способность балансировки.

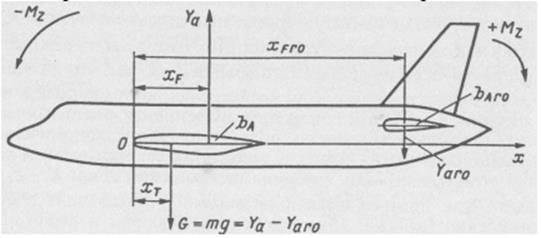
Балансировка – это обеспечение с помощью органов управления равенства 0 аэродинамических моментов относительно осей связанной системы координат (т.е. отсутствие вращения ЛА в полете относительно какой-либо оси). Однако за возможность балансировки ЛА приходится расплачиваться потерями аэродинамического качества. Рассмотрим, как это происходит.

Рисунок 15- Действие аэродинамических моментов на самолет

Подъемная сила ЛА приложена в точке центра давления ЛА, расположенной на средней аэродинамической хорде. Для самолетов нормальной аэродинамической схемы ц.д. находится позади ц.м. Поэтому относительно ц.м. подъемная сила создает момент, направленный вниз (пикирующий) – (-Мz). Для того, чтобы сбалансировать ЛА относительно оси OZ (не допустить его вращения) на ГО самолета должен быть создан уравновешивающий момент противоположного знака (кабрирующий) относительно ц.м. Этот момент создается подъемной силой на ГО в результате изменения угла его ус-

тановки или отклонения руля высоты.

Тогда сумма моментов относительно оси OZ:

А подъемная сила сбалансированного самолета уменьшает подъемную силу ЛА:

Для уравновешивания силы тяжести ЛА (Ya=mg) необходимо увеличить подъемную силу крыла путем увеличения угла атаки на величину Однако это приведет к увеличению индуктивного сопротивления. Кроме того, создание подъемной силы на оперении приведет к появлению индуктивного сопротивления на оперении. Если же балансировка осуществляется отклонением руля, то появляется еще одно дополнительное сопротивление – профильное сопротивление руля. В результате при балансировке суммарное сопротивление ЛА увеличивается на величину так называемого балансировочного сопротивления. Зависимость в этом случае уменьшает наклон, уменьшается максимальный коэффициент подъемной силы, а поляра ЛА сдвигается вправо – в сторону увеличения сопротивления, что в конечном итоге приводит к потере аэродинамического качества.

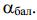
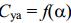
Рисунок 16- Зависимость коэффициента подъемной силы от угла атаки

Для уменьшения балансировочного сопротивления необходимо уменьшить потребный управляющий момент на оперении. Этого можно добиться уменьшением плеча силы Yа, на котором создается пикирующий момент: 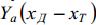. То есть либо сместить ц.м. назад, либо ц.д. вперед.
7.ВЛИЯНИЕ ЭКСПЛУАТАЦИОННЫХ ФАКТОРОВ НА ВЗЛЕТНО-

Дата добавления: 2016-02-02 ; просмотров: 5776 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

БАЛАНСИРОВКА САМОЛЕТА В УСТАНОВИВШЕМСЯ БОКОВОМ ДВИЖЕНИИ. ХАРАКТЕРИСТИКИ ПОПЕРЕЧНОЙ И ПУТЕВОЙ СТАТИЧЕСКОЙ УПРАВЛЯЕМОСТИ

Определим углы отклонения органов управления креном и рысканием, а также отклонения рычагов управления и усилия на них, потребные для балансировки самолета в установившемся боковом движении.

Балансировка самолета в установившемся прямолинейном полете со скольжением

Установившийся прямолинейный полет со скольжением выполняется при посадке самолета с боковым ветром, несимметрич­ном отказе двигателей и других случаях.

Для равновесия самолета необходимо, чтобы сумма моментов относительно связанных осей ОХ и 0Y, а также сумма проекций всех сил на поперечную ось 0Z были равны_нулю

MRx = 0; MRy = 0; = 0. (12.9)

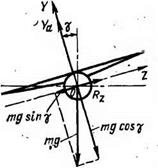
Рис. 12.6. Схема сил, действующих на самолет при полете с креном и скольжением
где Rz = Z + іРг, Z — поперечная аэродинамическая сила; Рг — поперечная составляющая тяги двигателя; і — число двигателей.

Из условия равновесия сил по оси 0Y (см. рис. 12.6)’имеем mg cos у їх Y ж Ya, откуда mg = YJcos у, и, тогда mg sin у = = Ya tg у. Следовательно, третье условие (12.9) запишется

Fz = Rz + Ya tg у = 4- Рг”6„ + Ya tg у = 0.

Так как Я*» = 0, то — ZV

Перейдем от сил и моментов к их коэффициентам, для чего разде­лим силы на Sq, а моменты на Sql. Значение коэффициентов моментов крена и рыскания приведены в (10.100) и (10.101). ►

т%у$ 4- тЪув6, 4- Щ? Ьп = 0;

С&*Р 4″ сг»8н 4″ суа г. п tg У = 0. cf 4- — *• •Ср

тивных двигателей и Сря ■■

Балансировочные значения углов 6„, б, и у определяются из системы (12.10) в зависимости от угла скольжения. Если в (12.10)

пренебречь малыми, величинами да*e, щь и трх, то получим

Потребные для балансировки самолета отклонения педалей хя и боковое отклонение ручки (штурвала) хя равны

u ___ б* ____ 0), а ручка (штурвал) влево (правый элерон вниз 6Э >0).

Из выражений (12.11)… (12.14) видно, что с увеличением степени поперечной и путевой статической устойчивости расходы руля направления, элеронов и рычагов управления растут.

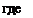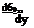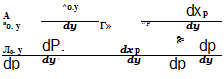Балансировочные значения бн, бэ. хн и ха можно выразить ив зависимости от угла крена. В этом случае

Так как d$/dy >0, то производные db0-y/dy и dxp/dy будут иметь такой же знак как dfi0. y/d|3 и dxv/d$. Значения производных d6„, y/dp, d$/dy и dxp/dfi определяются по формулам (12.12), (12.13) и (12.15).

Усилия на рычагах управления элеронами и рулем направления в прямолинейном установившемся полете со скольжением.

Усилие на ручке (штурвале) считается положительным (Рв >0), если летчик давит на ручку влево. При этом ручка отклоняется влево (хэ >0), а правый элерон вниз (6., >0).

Усилие на ручке при обратимой системе управления зависит от разности шар­нирных моментов, действующих на правый и левый элероны. Исходя из принципа

возможных перемещений получим #

Рц = — Кш. а Добр (Мш. пр — Мш. л) = — Аш. а^обр^вібд (Шш. эфф. прфпр —

где Кш. а = d&Jdxg; dxa — элементарное перемещение ручки; fe06p ^ 1 — коэф­фициент обратимости системы управления элеронами; 5Э1 — площадь одного эле­рона; Ь„ — САХ элерона; тш. Эфф. пр> тш. эфф. л — эффективные значения коэф­фициентов шарнирных моментов правого и левого элеронов; фпр, qn — эффективные значения скоростных напоров для правого и левого полукрыльев. Эффективные значения тш и q берутся в сечениях крыла, перпендикулярных линии фокусов.

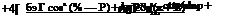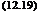После замены тш- Эфф и q для правого и левого элеронов и соответствующих преобразований выражение (12.18) запишется [9]

где Sa = 2S3l—площадь обоих элеронов; знак 6В берется по правому элерону.

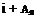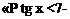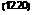Для небольших, по Сравнению с % углов Скольжения выражение (12.19) при­мет вид

Определим усилия на педалях при обратимой системе управления. За положи­тельное усилие принимается давящее усилие на правой педали (Рн > 0). В этом случае правая педаль отклоняется вперед (д:н > 0), а руль направления вправо (б., > 0).

Кш. Н^ОбрМщ. II — — ^Ш. іЛ)бртІН. н^п^н^в. оЯ’ (12.21)

где Кш. н = dS. i/dx,,; dxH — элементарное линейное отклонение педали; fe06p ^ 1 — коэффициент обратимости системы управления рулем направления.

тш. и = тшРв. о + тш 6,1 = тш (1 — ев) Р + тш»6н-

Рн = — *Ш. ЛвА6Л. о К 0 “ *5) Р + тш6н]

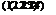
В пределах плавного обтекания при неотклонениом триммере коэффициент шар­нирного момента руля направления равен

Усилия на ручке и педалях, потребные для балансировки само­лета с обратимой и необратимой системо^ управления, можно пред­ставить в виде

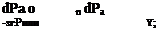
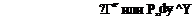Для обратимой системы управления производные усилия определяются путем дифференцирования выражений (12.23) и (12.24) по углу скольжения

Ф

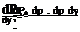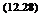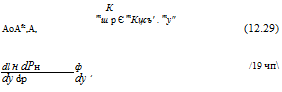
где dp/dy рассчитывается по формуле (12.13).

Так как при необратимой системе управления усилия, которые должен приложить летчик к рычагам, зависят от характеристик загрузочных механизмов, то эти производные будут иметь вид

Источник