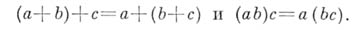что такое ассоциативность в математике

Ассоциативность

Содержание

В математике

В математике ассоциативность (также сочетательность) — свойство любой операции , такое что для неё выполняется равенство:

для любых элементов .

Например, ассоциативность операции умножения: .

В программировании

В программировании ассоциативностью (также очерёдностью) операторов называется последовательность их выполнения (или направление вычисления), реализуемое, когда операторы имеют одинаковый приоритет и отсутствует явное (с помощью скобок) указание на очерёдность их выполнения. При этом различается левая ассоциативность, при которой вычисление выражения происходит слева-направо, и правая ассоциативность — справа-налево. Соответствующие операторы называют левоассоциативными и правоассоциативными.

Например, в языке Python большинство операторов имеет левую ассоциативность, в то время как возведение в степень правоассоциативно:

Правая ассоциативность (вычисление выражения справа-налево), возведение в степень в языке Python:

Левая ассоциативность (вычисление выражения слева-направо), побитовый сдвиг в языке Python:

См. также

Ссылки

Полезное

Смотреть что такое «Ассоциативность» в других словарях:

ассоциативность — сослагательность; сочетательность Словарь русских синонимов. ассоциативность сущ., кол во синонимов: 1 • сочетательность (3) Словарь си … Словарь синонимов

АССОЦИАТИВНОСТЬ — (от средневекового лат. associatio соединение) ассоциативный (сочетательный) закон, свойство сложения и умножения, выражаемое формулами: (a + b) + c = a + (b + c), a(bc) = (ab)c … Большой Энциклопедический словарь

ассоциативность — АССО ИАТИВНЫЙ, ая, ое; вен, вна. Устанавливаемый по ассоциации (во 2 знач.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ассоциативность — (от ср. век. лат. associatio соединение), ассоциативный (сочетательный) закон, свойство сложения и умножения, выражаемое формулами: (а + b) + с = а + (b + с), a(bc) = (ab)с. * * * АССОЦИАТИВНОСТЬ АССОЦИАТИВНОСТЬ (от средневекового лат.… … Энциклопедический словарь

Ассоциативность — сочетательность, сочетательный закон, свойство операций сложения и умножения чисел, выражаемое тождествами (а + b) + c = a + (b + c) и (ab)c = a(bc). В общем смысле, действие а * b называется ассоциативным, если (а * b) * c = а * (b * с) … Большая советская энциклопедия

Ассоциативность — свойство многих математических операций. Сущность этого свойства понятна из следующих примеров: сложение ассоциативно, так как a + (b + c) = (a + b) + c, т. е. можно соединять в группы, ассоциировать отдельные слагаемые, составлять из них частные … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Ассоциативность — ж. отвлеч. сущ. по прил. ассоциативный 2. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

ассоциативность — ассоциативность, ассоциативности, ассоциативности, ассоциативностей, ассоциативности, ассоциативностям, ассоциативность, ассоциативности, ассоциативностью, ассоциативностями, ассоциативности, ассоциативностях (Источник: «Полная акцентуированная… … Формы слов

АССОЦИАТИВНОСТЬ — сочетательность, сочетательный зако н, свойство алгебраической операции. Для сложения и умножения чисел А. выражается тождествами Бинарная алгебраич. операция * ассоциативна (или, что то же, для * выполняется закон ассоциативности), если в данной … Математическая энциклопедия

АССОЦИАТИВНОСТЬ — (от ср. век. лат. associatio соединение), ассоциативный (сочетательный) закон, св во сложения и умножения, выражаемое ф лами: (а+b)+с=a+(b+с), а(bс) = (аb)с … Большой энциклопедический политехнический словарь

Источник

АССОЦИАТИВНОСТЬ

сочетательность, сочетательный зако н,- свойство алгебраической операции. Для сложения и умножения чисел А. выражается тождествами

Бинарная алгебраич. операция * ассоциативна (или, что то же, для * выполняется закон ассоциативности), если в данной алгебраич. системе справедливо тождество

для всех может быть определена А. для n-арной операции . О.

Смотреть что такое «АССОЦИАТИВНОСТЬ» в других словарях:

Ассоциативность — (от лат. associatio соединение) Содержание 1 В математике 2 В программировании 3 См. также … Википедия

ассоциативность — сослагательность; сочетательность Словарь русских синонимов. ассоциативность сущ., кол во синонимов: 1 • сочетательность (3) Словарь си … Словарь синонимов

АССОЦИАТИВНОСТЬ — (от средневекового лат. associatio соединение) ассоциативный (сочетательный) закон, свойство сложения и умножения, выражаемое формулами: (a + b) + c = a + (b + c), a(bc) = (ab)c … Большой Энциклопедический словарь

ассоциативность — АССО ИАТИВНЫЙ, ая, ое; вен, вна. Устанавливаемый по ассоциации (во 2 знач.). Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ассоциативность — (от ср. век. лат. associatio соединение), ассоциативный (сочетательный) закон, свойство сложения и умножения, выражаемое формулами: (а + b) + с = а + (b + с), a(bc) = (ab)с. * * * АССОЦИАТИВНОСТЬ АССОЦИАТИВНОСТЬ (от средневекового лат.… … Энциклопедический словарь

Ассоциативность — сочетательность, сочетательный закон, свойство операций сложения и умножения чисел, выражаемое тождествами (а + b) + c = a + (b + c) и (ab)c = a(bc). В общем смысле, действие а * b называется ассоциативным, если (а * b) * c = а * (b * с) … Большая советская энциклопедия

Ассоциативность — свойство многих математических операций. Сущность этого свойства понятна из следующих примеров: сложение ассоциативно, так как a + (b + c) = (a + b) + c, т. е. можно соединять в группы, ассоциировать отдельные слагаемые, составлять из них частные … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Ассоциативность — ж. отвлеч. сущ. по прил. ассоциативный 2. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

ассоциативность — ассоциативность, ассоциативности, ассоциативности, ассоциативностей, ассоциативности, ассоциативностям, ассоциативность, ассоциативности, ассоциативностью, ассоциативностями, ассоциативности, ассоциативностях (Источник: «Полная акцентуированная… … Формы слов

АССОЦИАТИВНОСТЬ — (от ср. век. лат. associatio соединение), ассоциативный (сочетательный) закон, св во сложения и умножения, выражаемое ф лами: (а+b)+с=a+(b+с), а(bс) = (аb)с … Большой энциклопедический политехнический словарь

Источник

В математике изобилие ассоциативных операций; фактически, многие алгебраические структуры (такие как полугруппы и категории ) явно требуют, чтобы их бинарные операции были ассоциативными.

СОДЕРЖАНИЕ

Определение

Формально бинарная операция ∗ на множестве S называется ассоциативной, если она удовлетворяет ассоциативному закону :

Обобщенный ассоциативный закон

Если операция произведения ассоциативна, обобщенный закон ассоциативности гласит, что все эти формулы дадут один и тот же результат. Таким образом, если формула с опущенными скобками уже имеет другое значение (см. Ниже), скобки можно считать ненужными, а «продукт» можно однозначно записать как

По мере увеличения количества элементов количество возможных способов вставки скобок быстро растет, но они остаются ненужными для устранения неоднозначности.

Примеры

Некоторые примеры ассоциативных операций включают следующее.

Логика высказываний

Правило замены

Функциональные связки истины

Совместное отрицание является примером функциональной связки истины, которая не ассоциативно.

Неассоциативная операция

Для такой операции порядок оценки имеет значение. Например:

Кроме того, хотя сложение ассоциативно для конечных сумм, оно не ассоциативно внутри бесконечных сумм ( рядов ). Например,

Неассоциативность вычисления с плавающей запятой

В математике сложение и умножение действительных чисел ассоциативно. Напротив, в информатике сложение и умножение чисел с плавающей запятой не является ассоциативным, поскольку при объединении значений разного размера возникают ошибки округления.

Чтобы проиллюстрировать это, рассмотрим представление с плавающей запятой с 4-битной мантиссой :
(1.000 ₂ × 2 0 + 1.000 ₂ × 2 0 ) + 1.000 ₂ × 2 4 = 1.000 ₂ × 2 1 + 1.000 ₂ × 2 4 = 1.00 1 ₂ × 2 4
1.000 ₂ × 2 0 + (1.000 ₂ × 2 0 + 1.000 ₂ × 2 4 ) = 1.000 ₂ × 2 0 + 1.000 ₂ × 2 4 = 1.00 0 ₂ × 2 4

Обозначения для неассоциативных операций

Левоассоциативная операция не является ассоциативной операцией, которая обычно вычисляются слева направо, т.е.

в то время как правоассоциативная операция обычно оценивается справа налево:

Встречаются как левоассоциативные, так и правоассоциативные операции. К левоассоциативным операциям относятся следующие:

Правоассоциативные операции включают следующее:

Неассоциативные операции, для которых не определен общепринятый порядок оценки, включают следующее.

История

Уильям Роуэн Гамильтон, кажется, ввел термин «ассоциативное свойство» около 1844 года, когда он размышлял о неассоциативной алгебре октонионов, о которых он узнал от Джона Т. Грейвса.

Источник

Ассоциативная операция

Ассоциати́вная опера́ция — это бинарная операция , обладающая ассоциативностью (лат. associatio — соединение), или сочетательностью:

для любых элементов .

Для ассоциативной операции результат вычисления не зависит от порядка вычисления (расстановки скобок), и потому позволяется опускать скобки в записи. Для неассоциативной операции выражение при 2″ border=»0″ /> в общем случае не определено.

История

См. также

Ссылки

Смотреть что такое «Ассоциативная операция» в других словарях:

ассоциативная операция — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN associative operation … Справочник технического переводчика

Бинарная операция — (от лат. bi два) математическая операция, принимающая два аргумента и возвращающая один результат (то есть с арностью два). Содержание 1 Определение 2 Замечание … Википедия

Коммутативная операция — Первое известное использование термина коммутативность … Википедия

ОБОБЩЕННАЯ ФУНКЦИЯ — математическое понятие, обобщающее классич. понятие функции. Потребность в таком обобщении возникает во многих технич., физич. и математич. задачах. Понятие О. ф. дает возможность выразить в математически корректной форме такие идеализированные… … Математическая энциклопедия

Сложение (математика) — У этого термина существуют и другие значения, см. Сложение (значения). Сложение (прибавление) одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае два числа). Более … Википедия

Источник

Ассоциативное свойство

В математике изобилие ассоциативных операций; фактически, многие алгебраические структуры (такие как полугруппы и категории ) явно требуют, чтобы их бинарные операции были ассоциативными.

СОДЕРЖАНИЕ

Определение [ править ]

Формально бинарная операция ∗ на множестве S называется ассоциативной, если она удовлетворяет ассоциативному закону :

Обобщенный ассоциативный закон [ править ]

Если операция произведения ассоциативна, обобщенный закон ассоциативности гласит, что все эти формулы дадут один и тот же результат. Таким образом, если формула с опущенными скобками уже имеет другое значение (см. Ниже), скобки можно считать ненужными, а «продукт» можно однозначно записать как

По мере увеличения количества элементов количество возможных способов вставки скобок быстро растет, но они остаются ненужными для устранения неоднозначности.

Примеры [ править ]

Некоторые примеры ассоциативных операций включают следующее.

Логика высказываний [ править ]

Правило замены [ править ]

Функциональные связки истины [ править ]

Совместное отрицание является примером функциональной связки истины, которая не ассоциативно.

Неассоциативная операция [ править ]

Для такой операции порядок оценки имеет значение. Например:

Также обратите внимание, что бесконечные суммы обычно не ассоциативны, например:

Неассоциативность вычисления с плавающей запятой [ править ]

В математике сложение и умножение действительных чисел ассоциативно. Напротив, в информатике сложение и умножение чисел с плавающей запятой не является ассоциативным, поскольку при объединении значений разного размера возникают ошибки округления. [8]

Чтобы проиллюстрировать это, рассмотрим представление с плавающей запятой с 4-битной мантиссой :
(1.000 ₂ × 2 0 + 1.000 ₂ × 2 0 ) + 1.000 ₂ × 2 4 = 1.000 ₂ × 2 1 + 1.000 ₂ × 2 4 = 1.00 1 ₂ × 2 4
1.000 ₂ × 2 0 + (1.000 ₂ × 2 0 + 1.000 ₂ × 2 4 ) = 1.000 ₂ × 2 0 + 1.000 ₂ × 2 4 = 1.00 0 ₂ × 2 4

Обозначения для неассоциативных операций [ править ]

Как правило, круглые скобки должны использоваться для обозначения порядка оценки, если неассоциативная операция встречается в выражении более одного раза (если в нотации порядок не указан другим способом, например ). Однако математики согласны с определенным порядком вычисления для нескольких общих неассоциативных операций. Это просто условное обозначение, чтобы избежать скобок. 2 3 / 4 <\displaystyle <\dfrac <2><3>>>

Левоассоциативная операция не является ассоциативной операцией, которая обычно вычисляются слева направо, т.е.

в то время как правоассоциативная операция обычно оценивается справа налево:

Встречаются как левоассоциативные, так и правоассоциативные операции. К левоассоциативным операциям относятся следующие:

Правоассоциативные операции включают следующее:

Неассоциативные операции, для которых не определен общепринятый порядок оценки, включают следующее.

Источник